基于ABAQUS的边坡稳定性影响因素分析

岳梦蕾,刘光汉,欧阳天云,余红兵

(贵州新联爆破工程集团有限公司, 贵州贵阳 550002)

基于ABAQUS的边坡稳定性影响因素分析

岳梦蕾,刘光汉,欧阳天云,余红兵

(贵州新联爆破工程集团有限公司, 贵州贵阳 550002)

为了分析不同因素与边坡稳定性的相互关系,借助了ABAQUS有限元模拟软件通过强度折减法,采用控制变量的方法建立了仿真模型,分析了弹性模量、容重、边坡高度、坡面角、粘聚力以及内摩擦角单因素变化对边坡稳定性的影响,得到了不同参数下安全系数随影响因素数值变化的规律。计算结果表明:弹性模量的变化对边坡的稳定性影响不大,岩土的容重、边坡高度和坡面角与边坡安全稳定系数呈线性负相关,岩土的粘聚力和内摩擦角与边坡安全稳定系数呈线性正相关。

边坡稳定性;强度折减法;ABAQUS;控制变量法

0 引 言

边坡稳定性研究一直是岩土工程领域复杂的综合性工作。受到多种内外因素的影响,如何对影响边坡稳定性的各因素进行综合评价,进而指导工程实际,对人民生命财产安全和工程经济建设具有重要意义[1-2]。边坡稳定性计算是指用量化指标评定边坡的稳定与否,并对其进行危险性评价,以及可能变化发展的趋势,通过量化指标对边坡的工程设计提出指导性意见。之前学者一般采用极限平衡法分析边坡稳定性,该方法易于掌握,计算过程简单快捷,但需预先假定滑动面所处的工况条件,同时不能考虑岩土实际应力－应变关系,不能分析滑体内的应力、变形分布状况,具有较大的局限性。后期学者提出基于强度折减法的有限元边坡稳定分析方法,能够分析岩体本身的变形对边坡变形计稳定性的影响,同时能够考虑岩土的非线性本构关系,还能模拟边坡的滑坡过程及其滑移面形状以及岩土与支护结构的共同作用[3-5]。

本文将建立基于工程实例的ABAQUS有限元模型,对可能影响边坡稳定的6个因素(弹性模量、容重、粘聚力、内摩擦角、边坡高度、坡面角)通过强度折减法进行独立的数值仿真模拟,进而得出各个因素对边坡稳定的影响,为边坡的合理建设、稳定性预测提供科学依据[6-7]。

1 基于强度折减法的有限元基本原理

基于有限元基本原理,边坡稳定安全系数在强度折减法中定义为岩土的实际抗剪强度与临界破坏时折减后剪切强度的比值。即定义安全系数可以通过调整岩土的强度指标C和φ,如公式(1)、公式(2)所示(式中,CF为折减后的粘结力,φF为折减后的摩擦角,Ftrial为折减系数),对折减后的粘聚力和内摩擦角进行模拟仿真计算,当刚好达到边坡临界破坏极限时的折减系数即为边坡的安全系数Fs。此种工况下,边坡刚好达到临界破坏状态,安全系数数值等于对岩体的抗剪强度所进行的折减系数。本文以有限元数值迭代不收敛为主要判据,辅以塑性区贯通为补充,用边坡安全系数为判据对边坡稳定性进行分析。

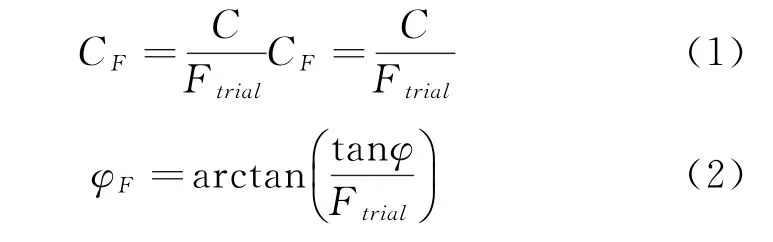
2 数值仿真模拟

2.1 模型建立

图1为某工程施工中一匀质的简单土质边坡,坡高为10m,坡角为45°,坡脚以下土层厚度为5 m,岩土材料服从Mohr－Coulomb破坏准则,根据工程试验取岩土容重为20kN/m3,弹性模量为100 MPa,泊松比为0.35,粘聚力c＝12.38kPa,内摩擦角φ＝20°,减胀角φ＝0°,建立计算模型,模型中单元采用8节点的平面应变缩减单元(CPE8R),基于ABAQUS模拟计算团建采用平面应变有限元理论通过强度折减法对该边坡进行稳定性分析。

图1 计算模型

2.2 计算结果分析

本文利用特征点位移来确定安全系数,选取坡顶靠近边坡的顶点作为特征点,得到其位移随折减系数的关系(见图2),图中当折减系数为0.5～0.99区间内变化时,边坡顶点未发生明显变化,当折减系数为0.99～1.02区间内变化时,边坡顶点质点开始发生下滑,折减系数为1.03时,顶点位移急剧增加,此时边坡的的塑性区已贯穿,如图3所示,表征边坡已失去稳定。通过塑性区形态和坡顶点位移与折减系数的关系,综合得出该边坡的安全系数为1.03。

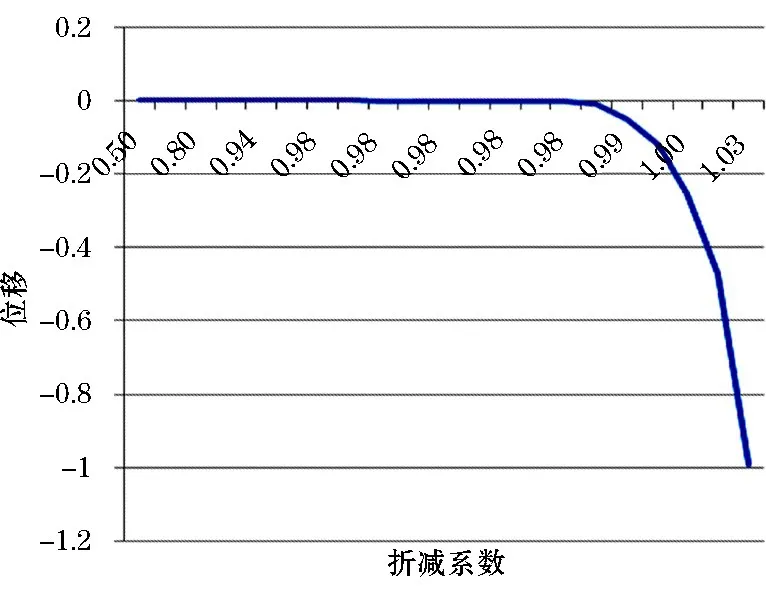
图2 坡顶点位移与折减系数的关系

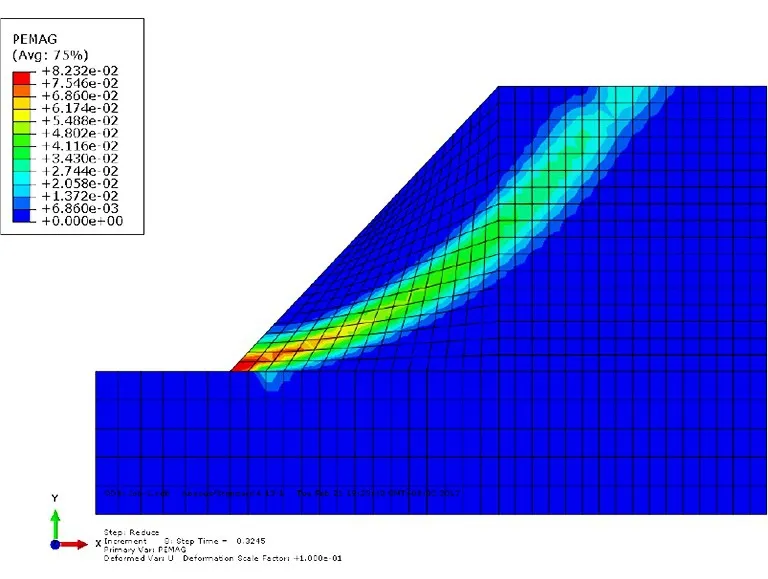
图3 折减系数为1.03时的塑性区

3 模拟不同因素对边坡稳定的影响

采用控制变量法,在其他条件不见得情况下,模拟单因素变化对边坡稳定的影响,以弹性模量、容重、边坡高度、坡面角、粘聚力、内摩擦角为影响因素,分别取40%、70%、100%、130%、160%作为单因素变化率,计算不同参数下模型的安全系数。计算结果如表1所示。

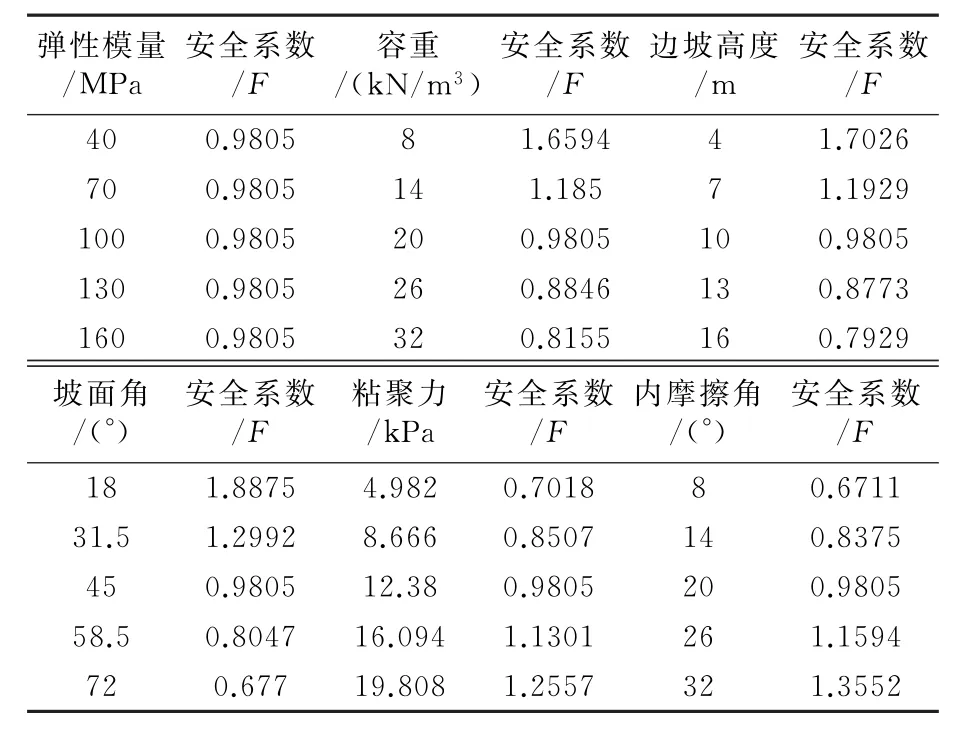
表1 单因素变化对边坡安全系数的影响

根据表1分别画出不同参数工况下对边坡安全系数的影响规律曲线,见图4～图9。

图4 弹性模量对安全系数影响

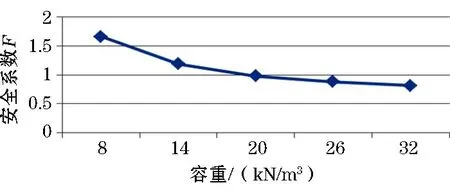
图5 容重对安全系数影响

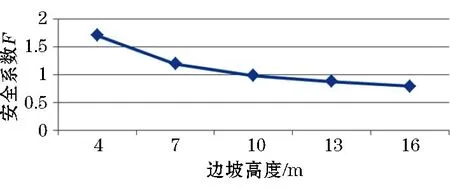
图6 边坡高度对安全系数的影响

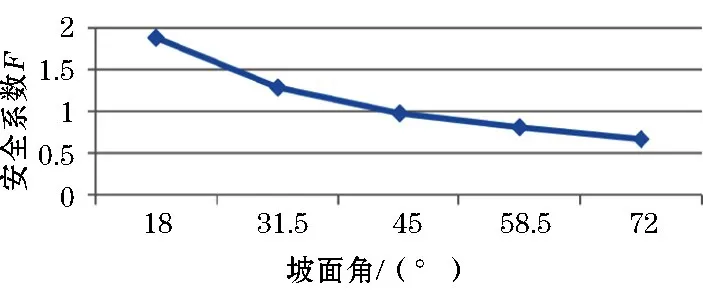
图7 坡面角对安全系数影响

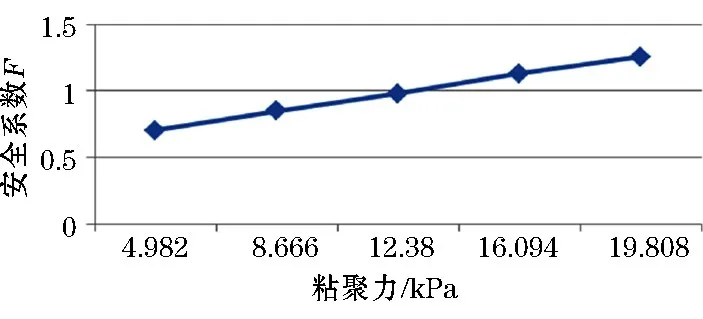
图8 粘聚力对安全系数影响

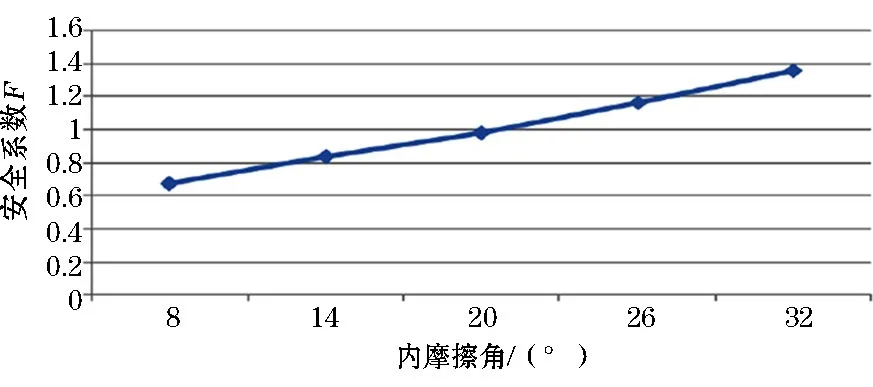
图9 内摩擦角对安全系数的影响

由图4～图9可以看出:

(1)安全系数不随弹性模量的变化而发生明显的变化,在一般的工程实例中,由于岩土的弹性模量均在一定取值范围内,而弹性模量表现为应力与应变的比值,其变化会影响变形,但不会影响应力场,而安全系数只依赖于应力场,表面弹性模量的大小并不能影响应用强度折减法求得的安全系数;

(2)随着容重的增加,边坡安全系数线性减小,这是因为当岩土容重增加时,坡体的重力增加,沿坡向的下滑力也随着增加,从而稳定性降低,安全系数减小;

(3)随着边坡高度的增加,边坡的安全系数线性减小,这是由于当边坡高度增加时,坡体的重力增加,其下滑力也必然增加,从而稳定性降低,安全系数减小;

(4)随着坡面角的增加,边坡的安全系数线性减小,这是由于,当坡面角增大后,沿坡向的下滑力增加,剪应力增大,边坡的稳定性降低,安全系数线性减小;

(5)随着粘聚力和内摩擦角的增加,边坡的安全系数线性增大,这是由于随着岩土粘聚力的增加(内摩擦角的增加),岩土的抗剪能力增大,抵抗滑坡的能力增加,安全系数增大。

4 结 论

岩土的弹性模量对边坡的稳定性基本无影响,岩土的容重、边坡高度和坡面角的量化值与边坡的稳定性安全系数性呈线性负相关,岩土的粘聚力和内摩擦角的量化值与边坡的稳定性安全系数性呈线性正相关。在实际施工中,路基填土应尽量选择容重小的岩土,并尽量降低边坡的高度,条件允许的前提下岩土应使坡面角尽可能小,以及选择强度高的岩土,对类此边坡工程实例中考虑不同边坡稳定性影响因素的权重大小分析中提出了指导意义。

[1]赵大千.安徽乌石山石灰岩矿设计采场终了边坡稳定性分析[J].采矿技术,2013,1(6):25-26,9.

[2]谷 岩.基于Geo_Slope露天边坡稳定性分析及治理方案选择[J].采矿技术,2016,16(4):22-23.

[3]侯俊伟,唐秋元,李杨秋,等.西南某山区机场高填方边坡稳定性研究[J].重庆交通大学学报(自然科学版),2016,35 (3):82-88.

[4]肖欣欣,李夕兵.FLAC3D在露天矿边坡参数优化中的应用[J].采矿技术,2012,12(2):73-75.

[5]胡 军,董建华,王凯凯,等.边坡稳定性的CPSO_BP模型研究[J].岩土力学,2016,37(S1):577-582,590.

[6]陈国庆,黄润秋,石豫川,等.基于动态和整体强度折减法的边坡稳定性分析[J].岩石力学与工程学报,2014,33(2): 243-256.

[7]王振伟,郝 哲,尚文凯,等.安家岭矿北帮滑坡区深部边坡稳定性分析与评价[J].采矿技术,2011,1(3):70-72.

2017-03-18)

岳梦蕾(1971－),贵州贵阳人,工程师,从事爆破事业管理工作,Email:602574716＠qq.com。