软岩巷道围岩变形力学响应特性分析
2017-07-24李新星
李新星
(广西壮族自治区建筑材料科学研究设计院, 广西南宁 530022)
软岩巷道围岩变形力学响应特性分析
李新星
(广西壮族自治区建筑材料科学研究设计院, 广西南宁 530022)
通过对软岩巷道围岩变形力学响应特性分析确定了弹塑性区应力、弹塑性位移、破碎区应力与破碎区半径的影响因素,并确定了与各因素之间的函数关系,为巷道支护提供了依据。结果表明,巷道围岩所受应力随着埋深的增大而增加,并且围岩产生的塑性范围和破碎区也相应增大。在巷道形成初期,需要立马对其进行支护处理,同时对围岩进行封闭。支护能够减小围岩所受应力,减小其围岩塑性范围和破碎范围的增加。在巷道围岩受力增加的起始时期,其塑性范围和和破碎范围增长速度相对平衡,当围岩受力达到一定程度时,围岩发生变形,塑性范围增长速度开始减缓,破碎范围扩大速度则相对增加。
软岩巷道;力学特性;塑性区;破碎区
0 前 言
软岩具有鲜明的岩石力学特性,其在一定应力状态下塑性变形异常明显。软岩当中的巷道围岩变形量明显、变化速度快,且表现出较长的持续性。由于软岩的这些特性,导致其围岩稳定性弱、巷道底板易发生底鼓等,对支护要求相应提高。对矿山安全生产带来一系列挑战。
围岩变形是由于顶板岩层的挠曲运动而引起支承压力重新分布所致。开采引起矿体上方顶板以一定的垮落角依次向采空区延伸,形成组合悬臂梁结构,悬露顶板及部分覆岩重量被转移到实体煤上,断裂岩梁在采空区内以冒落岩体为支点。黄艳利等根据井下矿压监测数据,对沿空留巷围岩与充填体的分阶段变形特征进行了分析[1-2]。赵勇等构建了软弱围岩隧道结构体系,并阐述了各个构件在该结构体系中的力学作用,建立了围岩应力释放的隧道结构体系理论模型[3-5]。朱庆华通过构建受采动影响下的软岩巷道围岩理论模型,并对其流变特性进行了分析,同时研究了巷道围岩力学分布特性及影响围岩稳固性特征的因素[6-9]。左清军等通过对不同掘进方法下隧道围岩变形在时空分布上的特性,得出了围岩径向变形速率在时空上的分布规律[10]。
本文在巷道围岩应力重新分布的基础上,建立围岩结构力学模型,根据弹塑性理论与强度准则得出塑性区与破碎区应力大小与半径,并得出不同开采阶段应力与半径的变化情况,为矿山生产实际提供了有效参考。
1 力学模型
软岩巷道顶板下沉、两侧帮内位移和变形与底鼓是显著的矿山压力作用的结果[11-12]。某地下矿山现场实际测量结果表明,巷道地板发生的底鼓量约占巷道顶板、地板位移总量的2/3。其产生的机理主要是在高地应力的影响下,巷道地板岩石支撑能力不足,岩体吸水变形及受到剪切破坏。所以,针对围岩变形力学响应特性进行分析是解决问题的关键。
巷道开挖后,围岩内发生应力重新分布,巷道周边附近是应力集中带,当巷道围岩受力达到某一范围时,其受力由内而外呈现明显的破碎区以及塑性区和弹性区。图1以圆形巷道作为示例。

图1 巷道围岩受力三区分布
塑性区岩体受力向内产生变形,在无支撑的情况下,将会导致岩体偏帮,继而会形成新的塑性区。根据塑性区的影响范围以及分布特性,制定相应的支护方案,是对地压进行有效管理的主要根据。
1.1 基本假设
(1)深部巷道、长度无限。埋藏深度Z不小于巷道等效半径的20倍,围岩自重对巷道受力产生的影响忽略不计,如图2所示,与原问题的误差不超过10%。在无限长的巷道长度里,围岩的性质一致。采用平面应变问题的方法,可以取巷道的任一截面作为其代表研究。
(2)原岩应力各向等压,见图2。(3)围岩为理想弹塑性体。
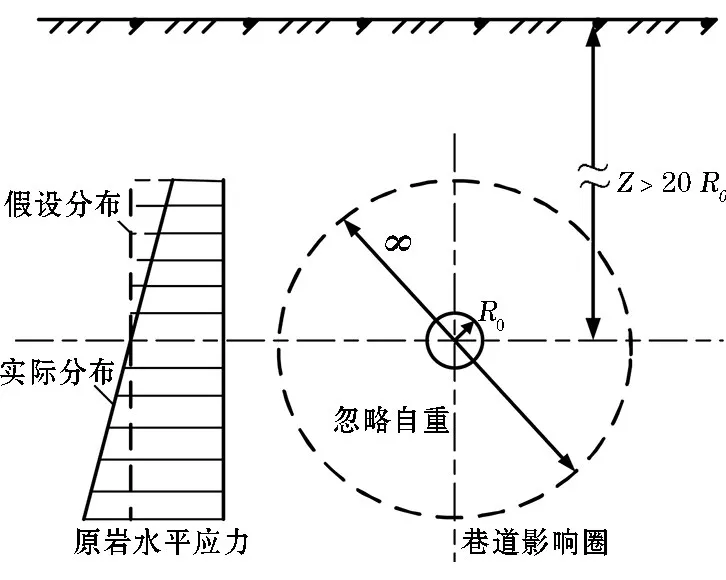
图2 深埋巷道的力学特点
根据围岩破坏机理及特征[13-14],对软岩巷道围岩结构进行简化,结合假设条件,建立围岩结构力学模型如图3所示。
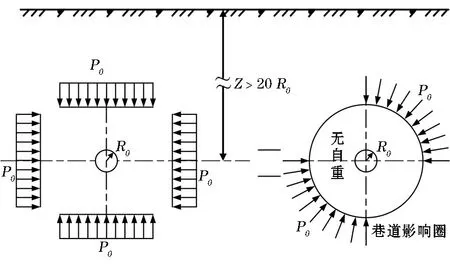
图3 轴对称巷道的受力条件
1.2 边界假设条件
1.2.1 弹性区
外部边界:r-∞,σr=σθ=p0(岩体原始应力)
内部边界(和塑性区交界的面):
r=Rp(塑性区半径)
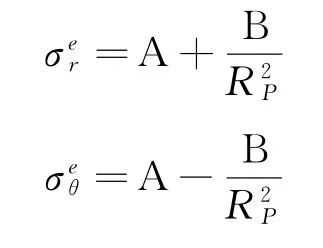
式中,σer、σeθ代表弹性区径向、切向方向上的应力; A、B是积分常数。
1.2.2 塑性区
外部边界(弹性区与塑性区相交的界面):
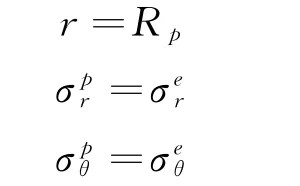
式中,e、p代表弹性区和塑性区的值。
内部边界:

1.3 公式推导
1.3.1 弹塑性区应力
为了找出对围岩变形影响较大的因素,将基本方程结合边界条件,当r=R,σ=0,σ=0rθ=σc,刚好和单轴抗压强度相等,而且σr,σθ和P0没有关系,只与强度准则有关。从弹性应力解和塑性区边界条件得出:

由式(2)、式(3)式可得:弹塑性区应力与巷道半径,底板岩体的内摩擦角,底板岩体的平均粘结力有关。弹塑性位移与底板岩体的内摩擦角,巷道半径,原岩压力,泊松比,弹性模量,内聚力有关。破碎区应力与残余变形阶段的内摩擦力和摩擦角,巷道半径有关。破碎区半径与残余变形阶段的内摩擦力和摩擦角,巷道半径,支护反力,泊松比,原岩压力,弹性模量,扩容系数有关。
1.3.2 弹塑性位移
巷道围岩的弹塑性位移,是支护主要解决的问题。弹塑性区域岩体形状的改变将导致其发生位移变化,弹性区形状的改变可以按照内边界半径为Rp的厚壁圆筒进行假设。
根据公式(2)、(3),可计算出弹塑性边界的位移为:
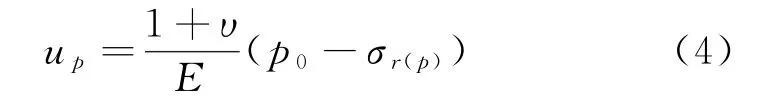
式中,σr(p)是弹塑性边界上的径向应力。根据塑性区体积不变的假设,有:
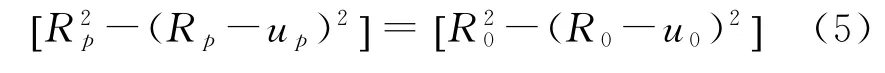
由此可以推导出巷道周边的位移公式:
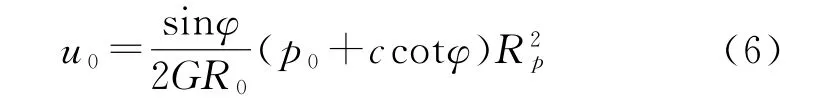
1.3.3 破碎区应力
在围岩破碎区,假定扩容系数为ξ,并假设围岩中内摩擦角不变,仍然满足库仑强度准则,则:
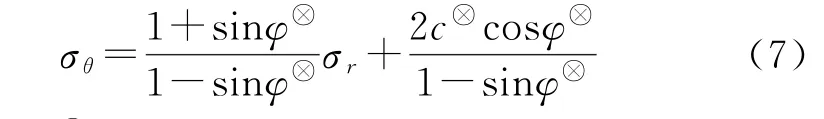
式中,c⊗、φ⊗为岩体在残余变形阶段的内摩擦力和摩擦角。
在无支护条件下,破碎区应力计算公式见式(8)~式(9),破碎区半径计算公式见式(10)。
有支护反力R1时,破碎区应力计算公式见式(11),破碎区半径计算公式见式(12)。
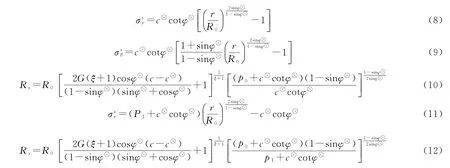
随着不断开挖,地应力逐渐增大,根据上文推导所得公式作出的塑性区半径及破碎区半径与地应力的关系如图4~图5所示。
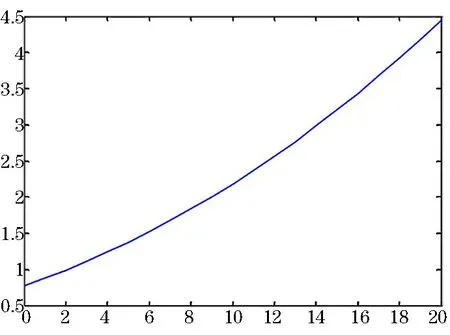
图5 破碎区半径变化
从图4和图5得出,随着围岩所受应力逐渐增大,巷道围岩慢慢开始发生变形以致破坏,塑性区增长速度减缓,破碎区增长速度有所增加,由此能够得出围岩破碎区的增大是导致深部软岩巷道围岩发生变形破坏的主要因素。
2 力学分析
某地下矿山巷道围岩是紫红色页岩,巷道形态设计为三心拱,等效半径R0=4.8m,其围岩性质为各向同性且等质,同时围岩受到静水产生的压力, P0=8.32MPa,根据矿山原始地质数据以及岩石室内试验测得数据得到页岩相关的力学参数及物理参数:c=14.09MPa,φ=38.870,υ=0.22,E=9.47 GPa,c⊗=0.015,ξ=2.8。
由公式(3)可得:Rp=4m;根据公式(12)可得: Rs=2.17m。由此可知,巷道围岩塑性区宽度大约为4m,破碎区宽度为2.17m。
由塑性区和破碎区应力推导公式可以得出:巷道围岩所受应力随着埋深的增大而增加,并且围岩产生的塑性范围和破碎区也相应增大,在巷道围岩受力增加的起始时期,其塑性范围和和破碎范围增长速度相对平衡,当围岩受力达到一定程度时,围岩发生变形,塑性范围增长速度开始减缓,破碎范围扩大速度则相对增加。
随着开采深度的增加,巷道围岩应力也相应加大。巷道围岩弹性区应力的增长梯度与静水压力的增长幅度相等或两者呈现线形关系;巷道围岩塑性区应力的增长梯度与静水压力的增长幅度呈现近似的线形关系;巷道围岩破碎区的岩体处于残余应变阶段,剪胀应力和扩容膨胀应力的增长速度较快,这就要求在开巷后必须充分释放围岩的变形能,永久支护也必须安排在巷道围岩变形稳定后进行。
由岩石力学理论和对现场巷道围岩位移的观测结果可知,在巷道围岩应力加大的初期阶段,破碎区的增长速率与塑性区的增长速率均衡,但随着巷道围岩应力的进一步加大,巷道围岩变形破坏,塑性区的增长速率下降,而破碎区的增长速率相对提高。可以看出,深井软岩巷道围岩变形的主要原因是围岩破碎区的增大。因此,在选择支护形式时,必须能限制围岩破碎区的扩展,考虑支护体既有一定的柔性,而且其强度和刚度又与围岩相匹配。
3 结 论
(1)通过公式推导与分析确定了弹塑性区应力、弹塑性位移、破碎区应力与破碎区半径的影响因素,并确定了与各因素之间的函数关系,为巷道支护提供了依据。
(2)巷道围岩所受应力随着埋深的增大而增加,并且围岩产生的塑性范围和破碎区也相应增大。在巷道形成初期,需要立马对其进行支护处理,同时对围岩进行封闭,以防膨胀性围岩发生分化。支护能够减小围岩所受应力,减小其围岩塑性范围和破碎范围的增加。
(3)在巷道围岩受力增加的起始时期,其塑性范围和和破碎范围增长速度相对平衡,当围岩受力达到一定程度时,围岩发生变形,塑性范围增长速度开始减缓,破碎范围扩大速度则相对增加。
[1]黄艳利,张吉雄,巨 峰.巷旁充填沿空留巷技术及矿压显现规律[J].西安科技大学学报,2009,29(5):515-520.
[2]康红普,牛多龙,张 镇,等.深部沿空留巷围岩变形特征与支护技术[J].岩石力学与工程学报,2010(10):1977-1987.
[3]赵 勇,刘建友,田四明,等.深埋隧道软弱围岩支护体系受力特征的试验研究[J].岩石力学与工程学报,2011,30(8): 1663-1670.
[4]赵旭峰,王春苗,孔祥利,等.深部软岩隧道施工性态时空效应分析[J].岩石力学与工程学报,2007,26(2):404-409.
[5]李英杰,张顶立,宋义敏,等.软弱破碎深埋隧道围岩渐进性破坏试验研究[J].岩石力学与工程学报,2012,31(6):1138-1147.
[6]高明中,王新丰,李 彦.顾桥矿深部巷道围岩变形破坏特征及稳定性控制技术[J].安徽理工大学学报(自然科学版), 2014(04):26-33.
[7]刘泉声,卢兴利.煤矿深部巷道破裂围岩非线性大变形及支护对策研究[J].岩土力学,2010(10):3273-3279.
[8]张学臣,李大勇,陈士海,等.跨采巷道的围岩稳定性预测与控制[J].采矿与安全工程学报,2008(03):361-365.
[9]高文华,朱建群,张志敏,等.软质岩石地基承载力试验研究[J].岩石力学与工程学报,2008,27(5):953-959.
[10]张广超,何富连.深井高应力软岩巷道围岩变形破坏机制及控制[J].采矿与安全工程学报,2015,32(04):571-577.
[11]高召宁,孟祥瑞.深井高应力软岩巷道围岩变形破坏及支护对策[J].中国煤炭,2007(01):8-11.
[12]赵 飞,杨双锁,李 平,等.深部高应力软岩巷道底鼓控制技术研究[J].矿业安全与环保,2015(2):104-107.
[13]赵国贞,马占国,孙 凯,等.小煤柱沿空掘巷围岩变形控制机理研究[J].采矿与安全工程学报,2010,27(04):517-521.
[14]余伟健,王卫军,黄文忠,等.高应力软岩巷道变形与破坏机制及返修控制技术[J].煤炭学报,2014,39(04):614-623.
2017-04-26)
李新星(1985-),男,江西鹰潭人,工程师,主要从事开采工艺理论及技术,Email:csuqyg@163.com。
