颗粒流程序开发及岩石类材料宏细观参数研究
2017-07-24彭宁波
彭宁波,孙 博
(1. 淮阴工学院 建筑工程学院,江苏 淮安223001; 2. 中铁西北科学研究院有限公司,兰州 730000)
颗粒流程序开发及岩石类材料宏细观参数研究
彭宁波1,孙 博2
(1. 淮阴工学院 建筑工程学院,江苏 淮安223001; 2. 中铁西北科学研究院有限公司,兰州 730000)
颗粒流程序可将细观物理力学性质参数与宏观力学参数联系起来模拟连续介质的基本力学特性,粘结单元模型可实现细观层面上对岩土体的损伤、破裂等过程以及破坏机制进行研究。针对目前的商用颗粒流软件中存在颗粒单元单一,粘结模型参数较多且无物理意义等不足,介绍了一种使用Fortran语言开发的颗粒流软件的开发。该程序包括棒状、圆盘状、任意多边形等基本形状的颗粒单元,通过初始孔隙率调整单元间的叠合量来控制粘结力的大小,避免计算时需要输入实验无法测定的粘结模型参数;同时,对于岩石材料的宏细观参数开展初步的研究,探讨不同宏细观参数之间的定性关系,为后续的相关研究工作奠定重要的基础。
颗粒流;岩石;单元形状;粘结模型;双轴实验
0 引言
离散元法(distinct element method,简称DEM)由Cundall[1]在1971年提出,是一种根据颗粒物质的离散特性建立起来的非连续介质数值模型,被广泛用来模拟开裂、断层等系统或颗粒材料在运动变形过程中速度场、位移场、力场等力学参量的变化。早期的离散元法[2]对岩体进行分析的过程中,假定块体单元为刚性,不考虑块体的变形及破坏过程,分析岩体的崩塌过程及评价结构整体的稳定性,适合研究关键块体在结构稳定性中的作用,但不能分析块体自身的变形、破坏特征。
岩石材料在外载荷作用下产生的损伤和破坏,是力学模型从连续体到非连续体的转变过程。颗粒流方法通过离散单元方法来模拟颗粒介质的运动及其相互作用,基于非连续介质理论将岩石类材料离散成刚性颗粒组成的计算模型,使从细观层面上对岩土体的损伤、破裂等过程以及破坏机制进行研究成为可能,它能监测模拟实验中岩石内部微裂纹的萌生、扩展及贯通整个过程。
目前,颗粒流软件中使用比较广泛的是Itasca公司开发的商业数值软件PFC(particle flow code)和PFC3D。在模拟岩石材料时,粒子间的接触关系可以处理成非粘结和粘结两种方式,当粘结强度达到一定程度时,粘结介质对粒子集合体基本特性的影响所起的作用就开始起到作用,这也是粒子流所研究的对象不局限于颗粒状介质的一个基本原因[3]。PFC中的粘结模型使用较多的是平行粘结模型[4-8],但颗粒流分析程序获得介质材料属性的手段不是通过预先设定的方式实现,而是通过“调配”颗粒组成及其接触状态的方式获得,需要单独设定粘结模型的弹性模量、粘结法向刚度与切向刚度比值、法向和切向粘结强度等粘结参数,颗粒间的粘结参数仅仅作为一个假想模型处理的,是获得连续介质的实现手段,因此,这些参数并没有实际的物理含义,且导致模型中引入的参数增多。PFC软件中颗粒单元只有圆形一种,如果需要考虑颗粒形状对模拟结果的影响,需要构造颗粒簇。再者,商业软件的可移植性较差,很多工作只能通过二次开发来进行[9-13],这为科研工作带来了诸多限制。
鉴于此,本文介绍了一种基于Fortran语言开发的颗粒流程序,该程序一方面可以基本实现商业软件的基本功能,另一方面实现现有商业软件不能实现的功能。另外,本程序具有良好的移植性,可以根据不同的问题,使用不同的控制方程和本构模型,为相关的科研工作提供极大方便,也能够为后续科研工作提供基础。
1 数值方法
1.1 颗粒流模型
本颗粒流程序中包含两类基本模型,一类为一般接触模型,此类模型用来模拟颗粒物质的运动规律,另一类为粘结模型,可以实现使用颗粒物质来模拟连续介质,如图1所示。

(a) 一般接触离散单元模型结果

(b) 粘结单元模型结果
一般接触模型对于颗粒间无重叠量的颗粒试样,颗粒与颗粒间只考虑表面接触力,对于颗粒间存在重合量的颗粒试样,颗粒间存在相互作用的排斥力,两个颗粒向相反的方向运动,如图1(a)所示。图1(b)所示为粘结单元模型,颗粒间的重叠量决定了颗粒间的粘结力,使用此种模型时,单元组件粘结成为一个整体,可以用来研究连续介质的开裂、破坏等力学行为。为模拟岩石的力学行为,本文主要介绍粘结模型的颗粒流程序。
1.2 单元形状
本程序中包含杆状单元、圆形颗粒单元和多边形单元,可以实现不同形状单元同时运算。图2显示了圆形和多边形的颗粒单元生成的岩石试样进行一维压缩试验的结果。由于不同单元形状还将影响试样整体的力链分布规律,导致同一位置的颗粒受力情况迥异,最终对计算结果的影响很大,因此,开发一种包含多种颗粒形状的颗粒流程序能够分析更为复杂的问题。
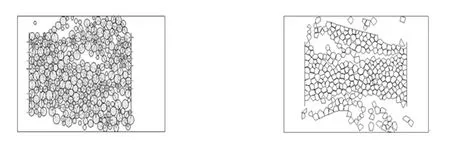
(a) 圆形颗粒试样一维压缩破坏 (b) 多边形颗粒试样一维压缩破坏
1.3 接触模型
由于包含了更多的单元形状,需要根据不同的接触类型,对不同形状颗粒的接触事件进行判断。接触类型包括杆-杆,杆-圆盘,杆-多边形,圆盘-圆盘,圆盘-多边形,多边形-多边形以及墙体单元与这几种形状单元的接触,如图3所示。

图3 不同形状单元的接触
另外,为了避免模型中设置过多的假想参数,本程序不采用单独的粘结参数控制颗粒间的粘结力,而是通过控制颗粒间的重叠量控制颗粒间的粘结力,如图4所示。在该粘结模型的法向和切向上,弹簧常数分别为Kn和Ks,阻尼常数分别为Cn和Cs,它们通过单位弹簧阻尼系统的参数获得,Kn=knB,Ks=ksB,Cn=cnB,Cs=csB,模型中,粘结力Fb由颗粒间的初始重叠量ub控制,Fb=Knub,现考虑粘结模型中的拉、剪两种类型的破坏模式,分别对应法向力Fn,切向力Fs。单元之间只要满足一种断裂的条件,单元即分为两个独立的单元,不再考虑粘结力,之后的运算中,将这两个单元按照一般的离散单元考虑。现在假设两个粘结单元的初始重叠宽度为ub,其中一个单元存在一个大小为u的位移矢量,则其法向力、切向力以及相对应的破坏准则分别通过以下运算获得,如图4所示。

图4 粘结单元模型
1.3.1 法向力与受拉破坏
当un大于-ub,法向力Fn按照下式进行计算,
(1)
当-ub< un< 0,Fn为负值,对应为拉力;当un≥ 0时,Fn为正值,对应为压力。当un≤ub,发生拉破坏,Fn=0。
1.3.2 切向力与受剪破坏
切向力Fs根据库伦摩擦定律确定,
(2)
2 双轴压缩实验
颗粒流程序可将细观物理力学性质参数与宏观力学参数联系起来模拟连续介质的基本力学特性,因此,建立起材料宏细观参数之间的关系非常重要,是颗粒流程序的开发及应用中需要验证的工作,也是后续研究的基础。对于岩石材料,通常通过双轴压缩模拟实验来建立起宏细观参数之间的关系。
2.1 试样的生成
通过颗粒进行组装生成岩石样品,过程如下:
(1) 在10mm×20mm的矩形区域内,随机生成粒径在1~3mm之间均匀分布(也可以根据需要生成不同粒径分布)的颗粒单元。
(2) 保持颗粒单元边界固定,设置一定的孔隙率,得到颗粒单元之间的初始重叠量,以控制不同岩石模型粘结力。由于在单元颗粒试样外构造了四个刚性无摩擦墙壁,不同单元重合量不同的颗粒试样对于墙体的反力大小不同,可以通过测量墙体单元上的合力大小来推算岩石试样的初始粘结力。
(3) 采用粘结单元模型,设定颗粒单元之间的摩擦系数,取消四周墙体上的位移约束,并在颗粒试样四周的墙体单元上施加初始压力(预压),如图5(a)所示。
(4) 保持左右两个墙体单元上面的初始压力,将下墙体单元固定,上部墙体上进一步施加力或位移条件,对试件进行压缩,如图5(b)所示。一般来说,为了方便控制,采用位移条件进行双轴压缩实验。
2.2 细观参数
表1为不同工况下输入的颗粒单元的细观参数。将墙体的刚度设置得足够大以模拟一个刚性的单元,这将影响到计算时步的选择,通常来说,刚度越大,计算时步越小,也必然导致计算机时的增大,所以,在实际计算中,需要注意控制刚度的大小。一般地,将刚性墙体的法向刚度和剪切刚度设置到109kN/m和108kN/m的数量级,既能够保证墙体的刚度,其计算机时也能够接受。
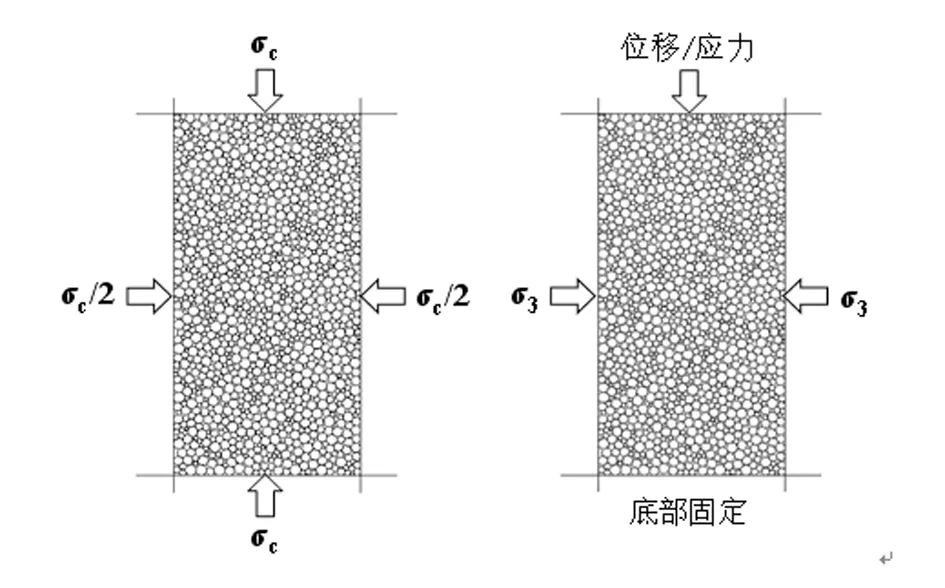
(a) (b)

密度ρ2.5kg/m2法向刚度kn1.0×107kN/m切向刚度ks2.5×106kN/m法向阻尼系数cn5.0×103kNs/m切向阻尼系数cs2.5×103kNs/m初始孔隙率e00.10/0.12/0.15颗粒单元之间的摩擦角度μ15/30/45/60Degrees
2.3 粘结强度
目前,普遍认为使用颗粒流程序模拟岩石双轴压缩实验时,颗粒单元的数量需要超过1000才具有实际意义[14]。这里建立了单元数量分别为1335、1311和1277的岩石样品,其初始孔隙率分别为0.10、0.12和0.15。获得样品生成时颗粒单元作用在周围墙体上的法向合力,如图6所示(以初始孔隙率0.10为例),随着计算时步的增加,作用在墙体上的法向力趋于常数,左右两面墙体上的作用力是上下两面墙体作用力的2倍,说明颗粒组件在墙体约束下,各向压强是一致的。

图6 e0=0.10时墙体上的初始法向作用力
则初始粘结强度可以根据下式求得:
(3)
其中,Fn是墙体单元上的法向力,W是墙体单元的长度。在孔隙率分别为0.10,0.12和0.15时,岩石试样的初始粘结强度是4.0×105kN/m,3.1×105kN/m,1.9×105kN/m。显然,随着孔隙率的增大,岩石试样的初始粘结力是减小的。
2.4 宏细观参数之间的联系
在实验过程中,上部墙体上的作用反力可以实时读取,通过多组双轴实验的模拟,不同围压将对应不同的主应力峰值,那么可以建立如图7所示的轴压与围压峰值之间的最优拟合关系曲线,岩石试样的粘聚力C和其内摩擦角φ可根据下式获得[14]:
(4)
(5)
其中,σi为纵坐标的截距,m为拟合曲线的斜率。
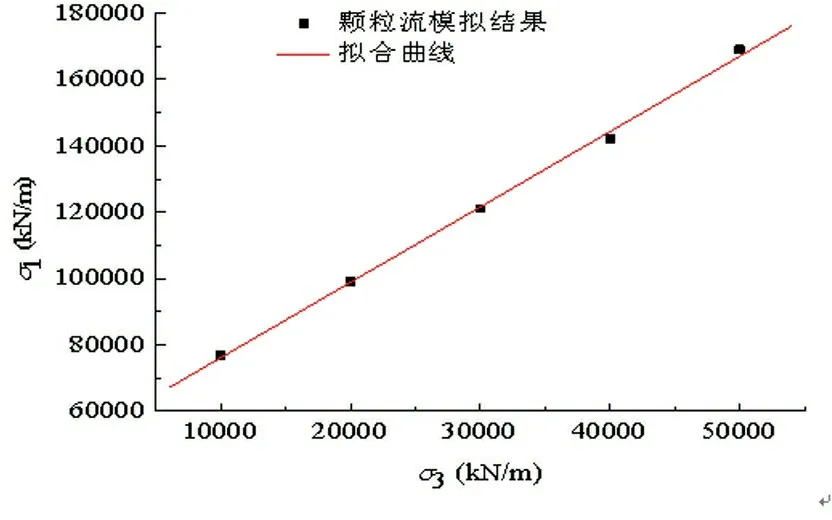
图7 围压与轴压之间的关系
选取e0=0.12,μ=30o工况作为一个案例,分析不同围压下岩石试样的应力-应变关系曲线模拟结果,如图8所示。可以看出,随着围压的增加,屈服应力和峰值强度整体呈现增加的趋势。
图9为初始孔隙率和围压不变的情况下(e0=0.12,σ3=3×104kN/m),不同颗粒单元摩擦角度条件下的应力-应变曲线结果。可以看出,随着颗粒间摩擦角度的增加,其应力峰值并不随之持续增大,当μ=60o时,应力峰值反而最小。在其他不同的工况下,可以获得类似的结果。
表1中的参数属于颗粒的参数,其中,刚度和阻尼系数属于颗粒流模型假定的参数,其取值存在一定的范围,但很难测定,通常做法是在一定范围内取值,并适当调整。而密度、孔隙率以及颗粒间摩擦角可看成颗粒物质中容易获得的实际参数,根据式(1)和式(2)可知,岩石的宏观参数C, φ由e0, μ确定,如表2中所列举的结果所示。但表中并没有呈现出这些参数之间的相互关系,但是可以定性判断的是,初始孔隙率主要影响粘聚力的大小,而颗粒间摩擦角主要影响岩石的内摩擦角。


图8 不同围压下的应力-应变曲线(e0=0.12 and μ=30o)
图9 不同颗粒单元摩擦角度下的应力-应变曲线(e0=0.12 and σ3=3×104kN/m)
为了获得宏观参数和细观参数之间的更清晰的关系,分别考虑初始孔隙率与粘聚力之间(图10),颗粒间摩擦角和岩石内摩擦角(图11)之间的关系。从图中可以分别看出,整体上粘聚力随着初始孔隙率的增加而减小,内摩擦角随着颗粒单元间的摩擦角增大而增大。μ=60o时,内摩擦角较大,但是粘聚力较小,而剪切强度是由粘聚力和内摩擦角共同决定的,这就可以解释图5中μ=60o下的屈服应力比其他几种情况小的原因。由于本文中数值模拟数据较少,还不能完全很好的描述出这些参数之间的确切关系,可以预见,在数据量足够的情况下,可以建立起它们之间的关系,从而为数值模拟中细观参数的选取提供依据,下一步需要开展更多的数值模拟实验。

表2 不同e0, μ对应的C, φ值
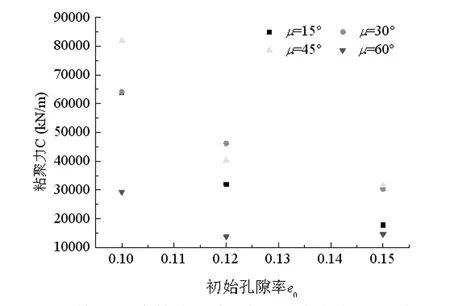
图10 不同颗粒单元间摩擦角下初始孔隙率与粘聚力之间的关系

图11 不同初始孔隙率下内摩擦角与颗粒单元间摩擦角之间的关系
3 结论
本文介绍了一种采用Fortran语言开发的颗粒流数值计算程序,相比较于目前比较流行的颗粒流商业软件,本程序中集合了杆状、圆形、多边形等形状的颗粒单元,并定义了多种形状颗粒单元之间的接触,能够根据问题研究的需要,选用不同的颗粒组合。在粘结模型中,不单独定义接触单元,而是通过初始孔隙率来调整单元之间的重叠量,控制颗粒间的粘结力,避免了设定无法通过实验确定的粘结参数。进一步,为了获得宏细观参数之间的关系,开展了双轴压缩实验,讨论了细观参数初始孔隙率和颗粒间摩擦角与宏观参数粘聚力和内摩擦角之间的关系。得到了如下结论:
(1)颗粒形状对于颗粒流模拟结果的影响很大,在模拟不同问题时,可以单独或组合选取不同形状的颗粒单元,以达到最好的模拟效果。
(2)在计算范围内,通过设定不同的初始孔隙率,能够很好的调整单元之间的叠合量,从而控制初始粘结力的大小,可不需要单独设定粘结单元,来调整获得所需的宏观参数,避免输入很多无实际物理意义且无法实验获得的粘结参数。
(3)初始孔隙率主要影响宏观参数粘聚力的大小,而颗粒间摩擦角则对宏观参数内摩擦角的影响较大。整体上,随着孔隙率的减小,粘聚力增大;随着颗粒间摩擦角增大,内摩擦角增大。如果需要更准确的定量关系,还需要在本文的工作基础上进一步增加大量的数值实验。
[1] CUNDALL P A. A computer model for simulating progressive large scale movements in blocky rock systems[C]//Proceeding of the Symposium of the International Society for Rock Mechanics. Rotterdam: Balkama A A, 1971 (1): 8-12.
[2] Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J].Geotechnique, 1979(1):47-65.
[3] 朱焕春.PFC及其在矿山崩落开采研究中的应用[J].岩石力学与工程学报, 2006(9):1927-1931.
[4] 丛宇,王在泉,郑颖人,等.基于颗粒流原理的岩石类材料细观参数的试验研究[J].岩土工程学报, 2015(6):1031-1040.
[5] 杨庆,刘元俊.岩石类材料裂纹扩展贯通的颗粒流模拟[J].岩石力学与工程学报, 2012(A01):3123-3129.
[6] 刘顺桂,刘海宁,王思敬,等. 断续节理直剪试验与 PFC2D 数值模拟分析[J].岩石力学与工程学报, 2008(9):1828-1836.
[7] 徐金明,谢芝蕾,贾海涛.石灰岩细观力学特性的颗粒流模拟[J].岩土力学,2010(sup.2): 390-395.
[8] 徐文杰,胡瑞林,王艳萍.基于数字图像的非均质岩土材料细观结构 PFC2D 模型[J].煤炭学报, 2007(4):358-362.
[9] 郑敏,蒋明镜,申志福. 简化接触模型的月壤离散元数值分析[J].岩土力学,2011(sup.1):766-771.
[10] JIANG Ming-jing, Konrad J M, Leroueil S. An efficient technique for generating homogeneous specimens for DEM studies[J]. Computers and Geotechnics,2003(7):579-597.
[11] Perko H, Nelson J, Sadeh W. Surface cleanliness effect on lunar soil shear strength[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001(4):371-383.
[12] 蒋明镜,付昌,刘静德,等. 各向异性结构性砂土离散元分析[J].岩土工程学报, 2015(1):138-146.
[13] 蒋明镜,陈贺,刘芳. 岩石微观胶结模型及离散元数值仿真方法初探[J].岩石力学与工程学报, 2013(1):15-23.
[14] Calvetti F., Combe G. and Lanier J. Experimental micromechanical analysis of a 2D granular material: relation between structure evolution and loading path[J]. Mechanics of Cohesive-Frictional Materials,1997(2):121-163.
[15] 付志亮. 岩石力学试验教程[M].北京: 化学工业出版社,2011.
(责任编辑:孙文彬)
Particle Flow Code Development and Study on the Macro-meso Parameters of Rock
PENG Ning-bo1,SUN Bo2
(1. Faculty of Architecture and Civil Engineering, Huaiyin Institute of Technology, Huai'an Jiangsu 223001, China; 2. Northwest Research Institute Co. Ltd. of China Railway Engineering Corporation, Lanzhou 730000, China)
Particle flow code mesoscopic physics mechanics parameters can be linked with macroscopic mechanical parameters of the simulation the basic mechanical characteristics of continuum, bonding element model which can realize the damage and fracture process of rock mass and failure mechanism at the mesoscopic level were studied. In view of the single particles in present commercial particle flow software unit, a lot of binding model parameters of the deficiencies is without physical meaning. In this paper, a particle flow using Fortran language development software development. The program includes basic shapes such as stick, disc, arbitrary polygon particles units, composite volume between the control unit is used to control the size of the cohesive force, greatly reduce the bonding parameters in the model; At the same time, the preliminary research of the macro mesoscopic parameters of rock material was conducted, the qualitative relationship between different macro mesoscopic parameters are discussed. The research of this paper has laid an important foundation for the follow-up research work.
particle flow code; rock; element shape; bonded modelling; biaxial test
2016-08-18
江苏省自然科学基金项目(BK20160426);淮安市科技项目(HAG201606)
彭宁波(1986-),男,江苏睢宁人,讲师,博士,主要从事岩土工程、环境工程研究。
TB472
A
1009-7961(2017)03-0041-07
