横看成岭侧成峰
——一道求轨迹方程考题的多角度探究
2017-07-21周胜田羿
周 胜 田 羿
(广东省中山市中山纪念中学,广东 中山 528454)
横看成岭侧成峰
——一道求轨迹方程考题的多角度探究
周 胜 田 羿
(广东省中山市中山纪念中学,广东 中山 528454)
平面解析几何的核心就是用方程的思想研究曲线,用曲线的性质研究方程.轨迹问题正是体现这一思想的重要表现形式.解析几何中求动点的轨迹方程问题是一个综合问题,涉及函数、方程、三角、平面几何等基础知识,是高考数学考查的重点内容之一.本文从不同角度探究了一道解析几何轨迹问题的七种解法,希望同学们能从中熟悉基本方法,拓宽解题思路,又能培养分析问题、解决问题的能力.
轨迹方程;斜率;参数法;交轨法;点差法
中山市高一年级2013-2014学年度第二学期期末统考数学试卷第20题如下:
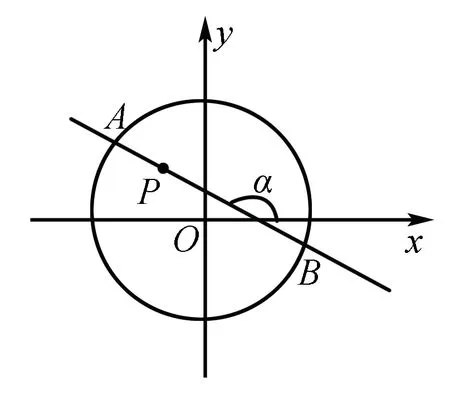
如图,圆x2+y2=8内有一点P(-1,2),AB为过点P倾斜角为α的弦.
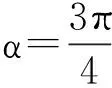
(2)当弦AB被点P平分时,写出直线AB的方程;
(3)求过点P的弦AB的中点的轨迹方程.
本文对该题第(3)问求轨迹方程的问题进行了多角度探究与总结,得到以下7种解决方案,与大家一起分享.
解法一 (参数法)当直线AB的斜率存在时,设其斜率为k,则直线AB的方程为
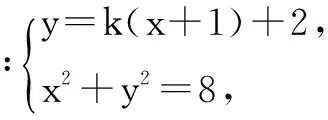
设A(x1,y1),B(x2,y2),弦AB中点M(x,y),则有:
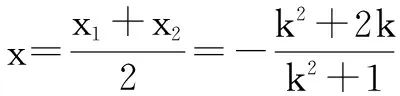

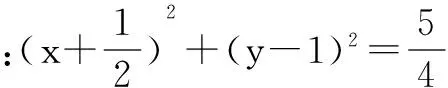

点评 联立方程,利用根与系数的关系是解决直线与圆锥曲线相交问题的基本方法.基本模式为:联立消元计算Δ值设出点的坐标韦达定理代入化简运算求解问题.但往往由于涉及字母较多,计算量大,运算技巧强,使得许多学生“易想难算”,望而生畏,产生恐惧心里,因此,对学生而言是一项艰巨的考验.
解法二:(交轨法) 当直线AB的斜率存在时,设其斜率为k,则直线AB的方程为
y-2=k(x+1),即y=k(x+1)+2
设弦AB中点M(x,y),则有OM⊥AB(O为坐标原点),所以OM所在直线方程为:
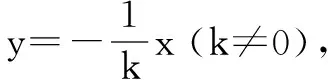
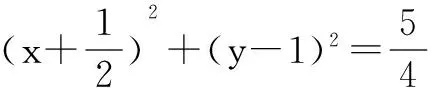
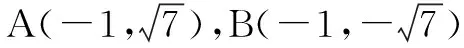
点评 交轨法是解析几何中求动点轨迹方程的常用方法.选择适当的参数表示两动曲线的方程,将两动曲线方程中的参数消去,得到不含参数的方程,即为两动曲线交点的轨迹方程.这种方法与解法一的想法类似,但是与解法一相比大大减少了化简过程中的计算量.
解法三:(直接法) 设弦AB中点M(x,y),由圆的性质知OM⊥AB

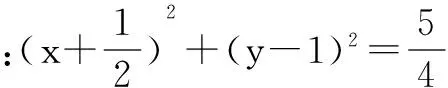
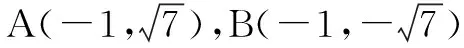
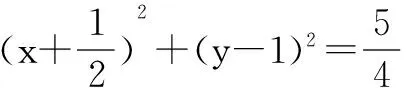
点评 用直接法求轨迹方程就是根据轨迹的条件,能够直接找到动点坐标之间的关系,从而得到所求的轨迹方程. 有时动点规律的数量关系不明显,这时可借助平面几何中的有关定理、性质、勾股定理、垂径定理、中线定理、连心线的性质等等,从而分析出其数量的关系,这种借助几何定理的方法是求动点轨迹的重要方法.



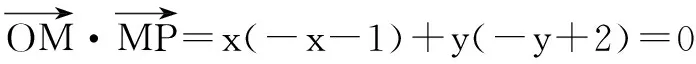
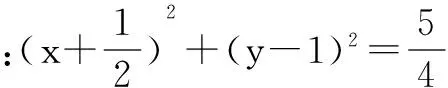
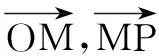
解法五:(几何法) 设弦AB中点M(x,y).
当O,P,M三点不共线时,连接OP,OM,则△OMP为直角三角形.由勾股定理得:OP2=OM2+MP2,
即 5=x2+y2+(x+1)2+(y-2)2,
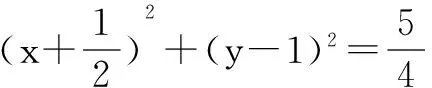
当O,P,M三点共线时,弦AB中点M与坐标原点重合,此时M(0,0)也满足上述方程.
点评 此解法充分利用直角三角形中三条边满足勾股定理,把边长满足的等量关系问题转化为代数方程问题,使学生思路开阔,熟练掌握知识的内在联系,从而培养思维的灵活性.这种解法与解法五类似,区别在于使用不同的方式转化垂直关系.
解法六:(定义法)设弦AB中点M(x,y)
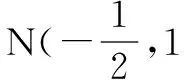

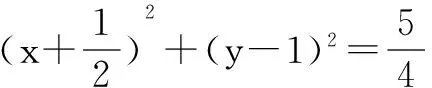
当O,P,M三点共线时,弦AB中点M与坐标原点重合,此时M(0,0)也满足上述方程.
点评 若动点在运动时满足的条件符合某种已知曲线的定义,则可以设出其轨迹的标准方程,然后利用待定系数法求出其轨迹方程.这种求轨迹方程的方法称为定义法.此解法充分利用几何图形的性质及特点,巧妙地进行转化,从而简化运算.这种解决问题的思想凸显解析几何的核心问题之一——几何问题.
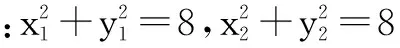
两式相减得:(x1-x2)(x1+x2)+(y1-y2)(y1+y2)=0.



中点M的坐标为(-1,0),也满足方程
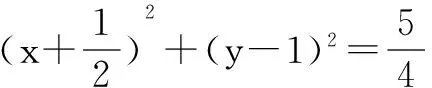
点评 点差法是解决圆锥曲线中“中点弦”问题的常用方法.在求解直线与圆锥曲线相交被截的线段中点坐标时,利用直线和圆锥曲线的两个交点,并把交点代入圆锥曲线的方程,再作差,然后将中点和斜率整体代入,即可得到相应的方程.设而不求和整体消元是解析法的重要思想和方法,可以简化很多繁琐的运算.
[1]谢全苗.试论数学解题的思维策略[J].中国数学教育:高中版,2008(9):40-42.
[2]赵思林.一道全国高考数学试题的多角度探究[J].数学通报,2009(11):25-30.
[3]吕水庚.一道高考试题的解法探究及教学思考[J].中学数学:高中版,2011(10):29-32.
[4]龚玉珍.例谈动点轨迹方程的求法[J].中学课程辅导·教学研究,2012(13):127-128.
[责任编辑:杨惠民]
2017-05-01
周胜(1981.10-),男,汉族,广东省中山市,硕士,中教一级,从事高中数学教学工作.
G632
B
1008-0333(2017)16-0013-03
