解圆锥曲线中最值问题的常用技巧
2017-07-21洪金华
洪金华
(浙江省温州市苍南县江南高级中学,浙江 温州 325000)
解圆锥曲线中最值问题的常用技巧
洪金华
(浙江省温州市苍南县江南高级中学,浙江 温州 325000)
圆锥曲线内容是高中几何的重要内容,也是高考重点考查的知识点之一,为使学生更好的解决这类问题,本文列举了几种常见解题技巧.
圆锥曲线;最值;技巧
最值问题向来都是出题者的“宠儿”,各个章节都存在.在圆锥曲线中也会经常遇到面积最大最小问题,距离最长最短问题,不定量的最大最小问题等等.解决这些最值问题应从函数、曲线、定义、不等式、几何、三角等多个角度去思考,选择恰当的途径.下面举例加以说明.
一、利用圆锥曲线的参数方程求最值
例1 已知点P是椭圆x2+8y2=8上到直线l:x-y+4=0的距离最小的点,则点P的坐标是( ).



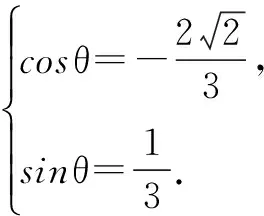
点评 利用参数方程,将原问题转化为三角问题,再用三角的有界性得出最值,然后返回求出P点坐标.
二、利用重要不等式求最值


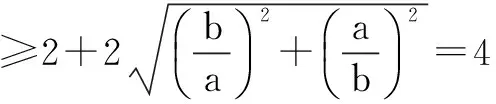
注意到等号可以成立,故应选A.
点评 分别求出互为共轭的双曲线离心率,再用不等式a2+b2≥2ab求最值,但不能忽视等号成立的条件.
三、利用圆锥曲线的定义求最值
解析 由双曲线的第一定义,得|PF1|-|PF2|=2a.
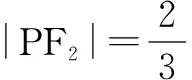
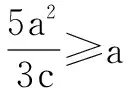

出关于a、c的不等式,从而得出e的取值范围.
四、利用圆锥曲线的对称性求最值

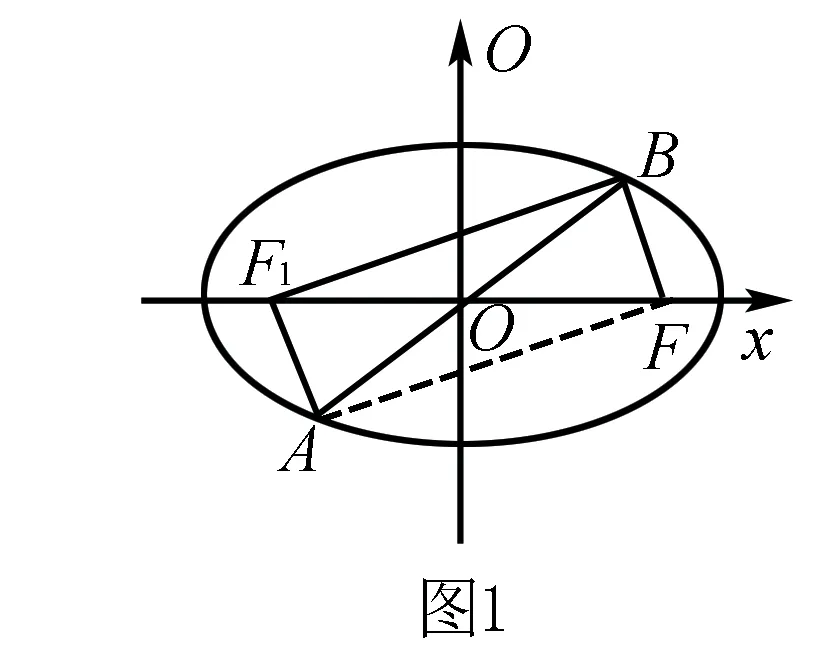
解析 如图1,由椭圆对称性知O为AB的中点,设椭圆右焦点为F,则四边形AFBF1为平行四边形.

∴△ABF1的面积最大值为bc.
点评 抓住椭圆是中心对称图形,从而得出四边形AFBF1为平行四边形这个结论.
小结:圆锥曲线是高中数学重要的学习内容,也是各地高考的必考内容,学生应该掌握常见的题型,同时还应该掌握一点解题技巧,在日常学习中一定要善于总结归纳,学会举一反三.
[1]宋贵聪.圆锥曲线中一类最值问题的解法[J].咸宁学院报,2009(6).
[2]王成西.圆锥曲线中最值问题的类型与解法[J].科技信息,2009(35).
[责任编辑 杨惠民]
2017-05-01
洪金华(1983.4-),男,江西上饶市婺源县,中学一级,大学本科,从事高中数学教学.
G632
B
1008-0333(2017)16-0052-02
