基于多元统计分析的出租车资源配置模型研究
2017-07-21孙丽男张璇张静刘德华
孙丽男++张璇++张静++刘德华

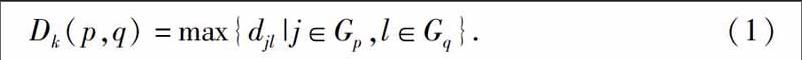

【摘要】利用打车软件智能出行平台获取相关数据,采用统计学方法分析不同时空出租车资源的“供需匹配”程度,为城市的出租车资源配置提供决策依据.首先,选取国内具有代表性的20个城市,利用聚类分析将其分为三类;其次,利用MATLAB对“出租车分布”和“出租车需求量分布”进行了可视化,直观分析了三类城市出租车资源“供需匹配”程度;最后,选取适当指标,利用SPSS对数据进行主成分分析及多元线性回归,建立了模型,量化了出租车资源“供需匹配”程度与相关指标的关系,从而可以通过控制各个指标来优化出租车资源配置.
【关键词】供需匹配程度;主成分分析;聚类分析;多元线性回归
【基金项目】2014年12月黑龙江省教育科学规划办重点课题,基于大数据技术的应用型本科院校统计学专业人才培养模式研究与实践(编号:GJB1214026).
随着人们生活水平的日益提高,城市交通网越来越发达,城市交通工具趋于多样性,私家车拥有量逐年飙升,尽管如此,受各种政策和客观条件的影响,出租车仍然是我国城镇市民出行重要的交通工具.由于出租车市场监管不够严格,城乡接合部面积扩张迅速等原因,一些城市出现了“打车难”现象,特别是流动人口多的旅游城市这种现象更加突出[1].为了缓解这一现象,打车软件应运而生并推出了许多优惠和补贴政策,一时间受到了广大司机和消费者的青睐.与此同时,打车软件智能出行平台内承载的海量数据也随着大数据时代的到来日渐凸显其重要的价值[2],通过对这些数据进行挖掘和分析必将对有效监管出租车市场的发展、合理配置出租车资源提供决策支持.针对我们要解决的实际问题,我们需要做以下模型假设:(1)假设打车软件系统无漏洞;(2)假设每个出租车公司出行政策相同;(3)假設每个地区软件平均使用率相同;(4)假设每个出租车行驶里程单价相同;(5)假设出租需求与供给不受天气影响;(6)假设道路交通里程数不变;(7)假设各个城市人口总数不变,出租车数量总数不变;
一、城市聚类分析
本小节选取聚类分析方法中系统聚类法[3]将一些重要城市聚类,为接下来的模型建立奠定基础.我们选取人口数、出租车拥有量等指标,利用系统聚类的分类方法将上海、北京、广州等20个主要城市进行聚类,将其分为三类,即一线交通发展城市、二线交通发展城市和三线交通发展城市.根据收集的统计数据,利用上述聚类方法,我们得到20个城市聚类后的树状图,从而我们可以得到聚类分析结果,见图1.
进一步,根据树状图和指标分布情况采用最长距离法进行分类.其中,最长距离法所使用的公式为
它等于Gp与Gq中最远的两个样品的距离.
根据最长距离法的定义及其公式,经过三次分类,最终将北京、广州聚为一类,定义为一线交通发展城市;沈阳、武汉、哈尔滨、济南、宁波、杭州、厦门和深圳聚为一类,定义为二线交通发展城市;剩余城市聚为一类,定义为相对发展较弱的三线交通发展城市.进行分类后,我们即可选取北京、沈阳和南京分别作为各类城市中的代表.
我们对北京、沈阳和南京三个城市的打车需求量与出租车分布利用MATLAB进行三维模拟,并进行两个指标间的比较.
由图2、图3可知,北京出租车分布情况的密集程度与需求量的分布程度部分地区基本一致,但总体差异性比较大,即北京的供求匹配不合理,需要重新合理分配出租车分布.南京出租车分布情况的密集程度与需求量的分布程度类似,但需求量很少,由此造成出租车空载率増大,资源浪费,因此,需要重新分配出租车分布以达到供需匹配平衡.沈阳分布出现的问题与南京相同,因此,需要调整出租车分布.
二、主成分分析[4]和多元线性回归模型
(一)模型建立
下面,我们将各城市出租车分布设为因变量y,难易度x1、需求量x2、抢单时间x3设为自变量,利用主成分分析对上述变量建立多元回归模型,具体步骤如下:
第一步,针对三个自变量做因子分析,计算出各指标的方差累积贡献率,得出x2与x3的累积贡献率大于85%,贡献率较高,x1的贡献率不高;
第二步,根据上述分析结果选取需求量x2、抢单时间x3作为因子,利用SPSS求得主成分prin1、prin2,见表2.
第三步,用y对两个主成分prin1和prin2做普通最小二乘,获得主成分系数,得到主成分回归方程为
(二)模型检验与分析
根据系数表,我们可知各个参数对应显著性检验的p值均小于显著性水平0.05,因此,上述模型通过检验.根据上述模型可知乘客对出租车的需求量与出租车的分布情况呈负相关,因此,出租车的分布与出租车的需求之间矛盾,造成出租车空载率增大,分布不合理,应有效改善出租车分布情况,提高利用率,尽可能地平衡分布与需求的关系.
(三)模型应用
下面我们通过对模型简单应用,进一步比较观测值和预测值,从而更直观地感受模型的回归效果及应用价值.
北京的模型应用:当难易度为9 452、需求量为707 154、抢单时间为604 100.55时,代入y=0.284x1-0.055x2+0479x3+56.181,得出租车分布为692 302,该数值与观测值相差不大,本模型预测效果较佳.
沈阳的模型应用:当难易度为2 857、需求量为294 228、抢单时间为20 594.38时,代入y=0.536x1-1.559x2+0049x3+41.806,得出租车分布为291 371,该数值与观测值相差不大,本模型预测效果较佳.
南京的模型应用:当难易度为4676、需求量为572 990、抢单时间为31 140.13时,代入y=-2.036x1-0.103x2+046x3+84.46,得出租车分布为568 314,该数值与观测值相差不大,本模型预测效果较佳.
除了上述模型的预测应用外,其还可以进行控制应用,即政府部门或相关企业要想控制某区域内的出租车分布,可以出台相应政策和措施调控难易度x1、需求量x2、抢单时间x3,进而达到调控出租车配置的目的.
【参考文献】
[1]潘玉奇,周劲,杨秀丽,袁宁.基于模糊聚类分析的数据检索的应用[J].微电子学与计算机,2005(06):167-169,172.
[2]林玉川.移动打车软件用户行为研究[D].厦门:厦门大学,2014.
[3]何晓群.多元统计分析[M].北京:人民大学出版社,2015.
[4]韩冰.主成分分析和神经网络在工业经济数据中的应用[D].长春:吉林大学,2014.
