解立体几何题的思路分析

梁华

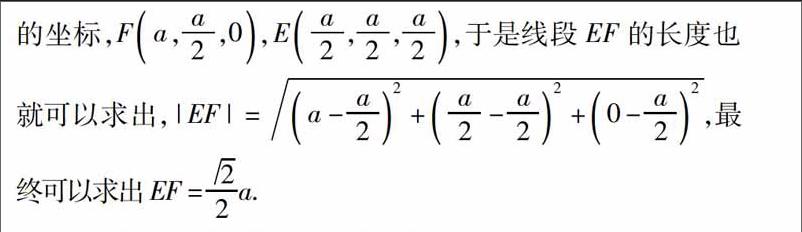
立体几何是数学中的一个重点知识，通过立体几何的相关习题的训练，既能够训练空间思维能力和想象逻辑能力，又能够锻炼数学计算能力，是培养数学思维能力的有效题目.对于立体几何的解题来说，不断进行习题解决的过程就是对知识不断巩固和重复的过程，解决立体几何的相关习题，既能复习所学知识，又能够应用新思想，拓展新思路.

一、数形结合，化抽象为具体

数形结合方法是数学中解决习题的一种常用方式，在数学的多种习题中都有应用，比如，函数类问题需要结合函数图像进行解决，椭圆、双曲线问题需要借助画图等，在立体几何中，数形结合方法也同样适用，甚至应用数形结合的方法可以使立体几何的习题更加简单化.数形结合方法就是指，在进行习题的解决过程中，将数学问题与立体几何的图形问题进行相互转化，将原本抽象的数学图形问题转换为图形与代数相结合的方式进行解决.通过数形结合的解题方法，可以使原本抽象的图形变得具体化、形象化、方便理解，从而使得解决问题的过程变得更加轻松.在立体几何中应用数形结合方法需要我们读懂题目，了解题目中图形的具体特征，能够根据图形的特点和规律构造相关的代数方程，最终通过解方程的形式解决立体几何的相关问题.

例1如图所示，在一个长方体房间中，一只蚂蚁要从房间的A点爬到C′点，已知长方体房间为6 m×8 m×10 m，求蚂蚁需要爬行的最短距离？

分析题目要求的是蚂蚁的最短路程，这是一个最短距离的问题，但是最短距离的问题只在平面图形中涉及，在立体几何中又该如何解决呢？于是解决问题的最简单有效的方法就是将立体几何的问题转化为平面图形的问题，进而通过代数运算进行解决.在这道题目中，可以将立体图形进行展开，于是所求的最短路程就是平面中线段AC′的距离，计算的方法就是AC′=（AD+CD）2+CC′2.这样，通过将立体几何的问题与代数问题进行结合，就可以使立体几何的问题变得简单、具体、易于理解.

二、向量计算，化复杂为简单

在立体几何的解决方法中，还有一种简单有效的解决问题的方法，就是向量计算法.向量计算法是指在利用立体几何的三视图以及斜二测图，通过在立体几何中建立三维坐标系，代入向量，应用数学知识以及数学语言，实现立体几何的计算的方法.立体几何的计算往往涉及平方计算、开方计算，在计算数据简单的情况下，平方与开方计算能够相对简单，但是在计算数据复杂的情况下，计算的难度就大幅度提升，计算的错误率也会随之提升，而在立体几何的计算中应用向量可以大大降低计算的难度.在立体几何的向量计算法中，需要对向量的位置关系以及数量关系进行判断，进而找出向量的夹角或者利用向量之间的平行以及垂直关系实现题目的计算.向量计算的方法在立体几何求解异面直线间距的问题时，可以有效减少计算的时间，同时大大提高解题的正确率.

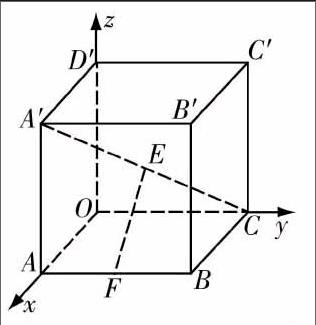
例2如图所示，在空间直角坐标系中，有一个正方体ABCO-A′B′C′D′，其棱长是a，则A′C的中点E与AB的中点F之间的距离为多少？

解析由于题目中给出了直角坐标系，显然是让我们利用向量法进行计算.由于题目的已知，所以不需要我们再建立直角坐标系进行计算，我们可以根据给出的图，找出所需要的点

三、分割补充，化杂乱为规则

在数学习题中，对图形进行分割或者补充来简化原本的题目也是一种数学思想.立体几何中的割补法就是这种数学思想的产物，割补法分为两个方面，分割：即将原来的立体图形进行分割，分割成多个易于计算的几何体，方便问题的解决.补充：即在原有立体图形的基础上，对原来的图形进行补充，使之成为一个易于观察的几何体，方便计算.不管是分割还是补充，其根本目的都是为了简化计算，从而将原本的不规则立体图形转换为规则的立体几何图形，通过这样的分割和补充的方法解决立体几何的问题，对数学思维以及空间想象能力的培养也大有好处，是一种高效、有益的解决数学问题的方法.

例3如图所示，有一个被平面截得的圆柱体，被截后，其最长的母线长为5，最短的母线长为2，且圆柱体的底面半径为3，求被截后的几何体的体积是多少？

分析对于这样的题目，我们在看到题目之后，知道该几何体是由圆柱体被截后得到的，那么要计算该圆柱体的体积，我们可以采用补充法，运用想象，我们将两个完全相同的几何体进行拼凑，使之成为一个完整的圆柱体，这样就能够通过求解圆柱体的体积，进而求出不规则几何体的体积，实现问题的解决.

总而言之，对于立体几何习题，只要掌握好解决的每一种方法：数形结合法、向量计算法以及割补法，那么立体几何的问题就能迎刃而解.面对立体几何的题目，應当保持冷静的心态，不应当被其烦琐的计算、复杂的思路所困扰，而是应当进行认真的审题、仔细的计算，在不断的练习中逐渐提高自身的数学逻辑能力以及空间想象能力，实现素养的提升.