用函数的观点求解数列问题

杨梅++甯懿楠

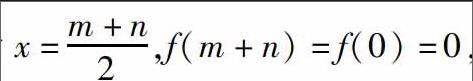
【摘要】教材将数列安排在函数之后学习，强调了数列与函数知识的密切关系，数列可看作一个定义域为N的函数，数列的通项公式就是相应的函数解析式；其图像表示的是一群孤立的点，因此，用函数的观点去考查数列问题也是一种有效的途径，本文将用函数的观点来解决数列的相关问题.

【关键词】函数；等差数列；二次函数

一、利用等差数列通项公式是一次函数形式的性质

对于公差不为零的等差数列来说，它的通项是关于n的一次函数，其公差就是这个一次函数（直线）的斜率，因此，可用此思想来求得数列的公差，进而求得数列中其他的量.

例1在等差数列{an}中，a5=-3，a15=27，求数列的通项公式.

分析本题中已知数列中的两项，求数列的通项公式，属于基础题，要求出数列通项的公式，应先求出公差d，再按公式写出通项.

解题思路联系等差数列的通项公式是关于n一次函数，且公差就是这个一次函数的斜率，题中已知的两项可看成两点（5，-3），（15，27），求出过这两点直线的斜率即为该数列的公差，则可求得数列的通项公式.

二、利用Sn是n的二次函数的性质

分析该题的题干较短，可提取的信息不多，对于我们解决问题有一定的困难，若直接用公式然后令它们相等来解决问题较难，不易突破.因此，可以联系公差不为零的等差数列的前n项和是关于项数n的二次函数，将数列问题用函数的思想求解.

解题思路（1）略.

（2）该题若从数列的角度解决有一定的困难，为了更方便地解决此题，我们可以从函数的角度思考利用公差不为零的等差数列前n项和与二次函数之间的关系可知对称轴为 ，即Sm+n的值为零.

反思上题第二问的解答方式利用了二次函数图像关于对称轴对称的性质，结合函数图像性质分析解决数列问题能使问题转变得更简单.

三、利用函数的性质解数列问题

数列是特殊的函数，函数基本性质包括：单调性、周期性、奇偶性、最值性，其中函数的单调性、周期性在数列中有广泛的应用.

（一）函数单调性在数列中的应用

解题思路由所求问题可知，首先应先求出an的形式，根據题中所给出的递推关系很容易判断出用累加法求通项，令f（n）=ann将所求问题转化为函数问题，再按求函数最值的方法求最值即可，但应注意此特殊函数定义域.

反思数列是一种离散型的函数，它的单调性与函数的单调性既有联系又有区别.在利用函数单调性解决数列的最值问题时要善于利用函数的图像和性质来分析数列问题，同时应注意数列的定义域.

（二）函数的周期性在数列中的应用

分析此题所要求解的是该数列的第2 008项，从题中给出的已知条件我们不能套用公式，因此，我们应从周期性的角度考虑，结合函数周期的确定方法来解决此问题.

解题思路题中给出的递推关系是连续三项之间的关系，我们可以令f（n）=an，联系题中已知的递推关系可以求出该函数的周期，用2 008除以周期再结合余数即可求出第2 008项的值.

反思本题主要考查数列的基本知识，关键在于发现所隐含的函数关系，利用周期性，从而达到解题的目的.

综上可见，在解决较难数列问题时，常常找不到解题的突破口，使思维受阻.我们知道数列是一类特殊的函数，若能将数列问题转化为函数问题来研究就很方便快捷.因此，当我们在解决数列问题时，要树立函数思想及观点，应充分利用函数的有关知识，以它的概念、性质以及图像为纽带，架起函数与数列之间的桥梁，揭示它们内在的联系和区别，从而更好地解决数列问题.

【参考文献】

[1]闫沛莲.函数观点下的数列问题[J].数学教学研究，2006（2）：24-26.

[2]周道平.用函数的知识解决数列问题[J].数理化学习：高三版，2013（12）：63.