基于系统动力学模型的备件供应系统计算实验研究

潘显俊， 张 炜， 赵 田， 苏金波

(1. 装备学院 光电装备系， 北京 101416； 2. 装备学院 研究生管理大队， 北京 101416； 3. 装备学院 装备指挥系， 北京 101416)

基于系统动力学模型的备件供应系统计算实验研究

潘显俊1,2， 张 炜3， 赵 田2， 苏金波2

(1. 装备学院 光电装备系， 北京 101416； 2. 装备学院 研究生管理大队， 北京 101416； 3. 装备学院 装备指挥系， 北京 101416)

为了提高备件供应系统效率，降低备件供应成本，实现备件供应“精确化”，以某型武器“基层级-基地级”两级保障模式为研究对象，分析影响基层级备件供应系统备件保障能力的主要因素，建立基层级备件供应系统动力学模型和系统动力学方程，进行了模型校验以保证模型的有效性。以备件入库延迟时间、出库延迟时间、供需差额反应时间和供需差额调整强度为实验因素，以平均库存量和供需差额绝对值均值为考察对象进行计算实验。实验结果表明：备件供应系统中较大的延迟时间和备件供需差额调整强度将导致备件库存水平较大波动，较大出库延迟时间将显著增加备件库存水平。

装备保障；备件供应；系统动力学；计算实验

优良的战备完好率是装备维修保障和备件供应的重要目标。如某型装备的维修保障模式主要采用“基层级-基地级”两级维修保障模式，其中基层级维修保障能力直接影响装备的战备完好率。基层级维修主要方式是进行直接换件维修，不进行部件的离位维修。在通常情况下，换件维修耗时短，装备的不可用时间主要取决于故障检测时间和备件等待时间，备件供应水平成为影响装备使用可用度和完好率的主要因素[1]。在基层级维修，主要是由备件短缺导致系统的可用度降低，直接影响装备的战备完好率，从而影响任务完成率。因此，科学合理的基层级备件存储和供应策略是提高装备完好率的重要保证。

目前，初始备件库存模型，主要以VARI-METRIC模型为基础，假设装备部件寿命分布为指数分布，备件需求数量为泊松分布[2-3]。也有学者在此模型基础上，对备件的库存优化方法进行了研究[4-5]。但是VARI-METRIC模型没有考虑在备件供应系统中的不同环节的延迟动态变化问题，备件供应系统是一个动态系统，VARI-METRIC模型无法描述其动态特性。该模型通常适用于装备论证阶段保障系统备件保障方案的初步设计和装备部署时初始备件方案设计。

备件短缺率增加，系统可用度降低，尤其是在基层级维修普遍采用换件维修的模式，备件短缺成为影响装备可用度的主要因素。备件的供应包括订货、接收入库、供应出库和备件使用等环节。备件供应系统的目标就是满足备件供应需求，同时降低备件库存成本。装备故障或者计划维修保养进行维修，需要消耗一定的备品备件，从而产生备件需求。在基层级，当一次故障或者一次计划维修需要进行换件时，即产生一次备件需求，因此将备件需求率作为备件供应系统的输入。利用系统动力学模型分析备件供应系统，分析备件供应系统要素和系统结构，建立备件供应系统中的物质流和信息流运行机制，探索备件库存控制的优化策略。

1 两级备件供应系统描述

典型的两级备件供应系统运行过程如图1所示。LRU(Line-Replaceable Unit)为外场更换单元，SRU(Shop-Replaceable Unit)为内场更换单元。基层级保障机构进行现场换件维修，不存储备件。装备LRU故障时，基层级保障机构向基地级保障机构进行备件申请，基地级保障机构供应LRU备件；备件送达时，基层级保障机构进行换件维修，并将故障LRU后送到基地级维修保障机构。基地维修机构负责故障LRU的修理，修理完好后的LRU送到备件仓库存储，同时负责LRU和SRU订购。

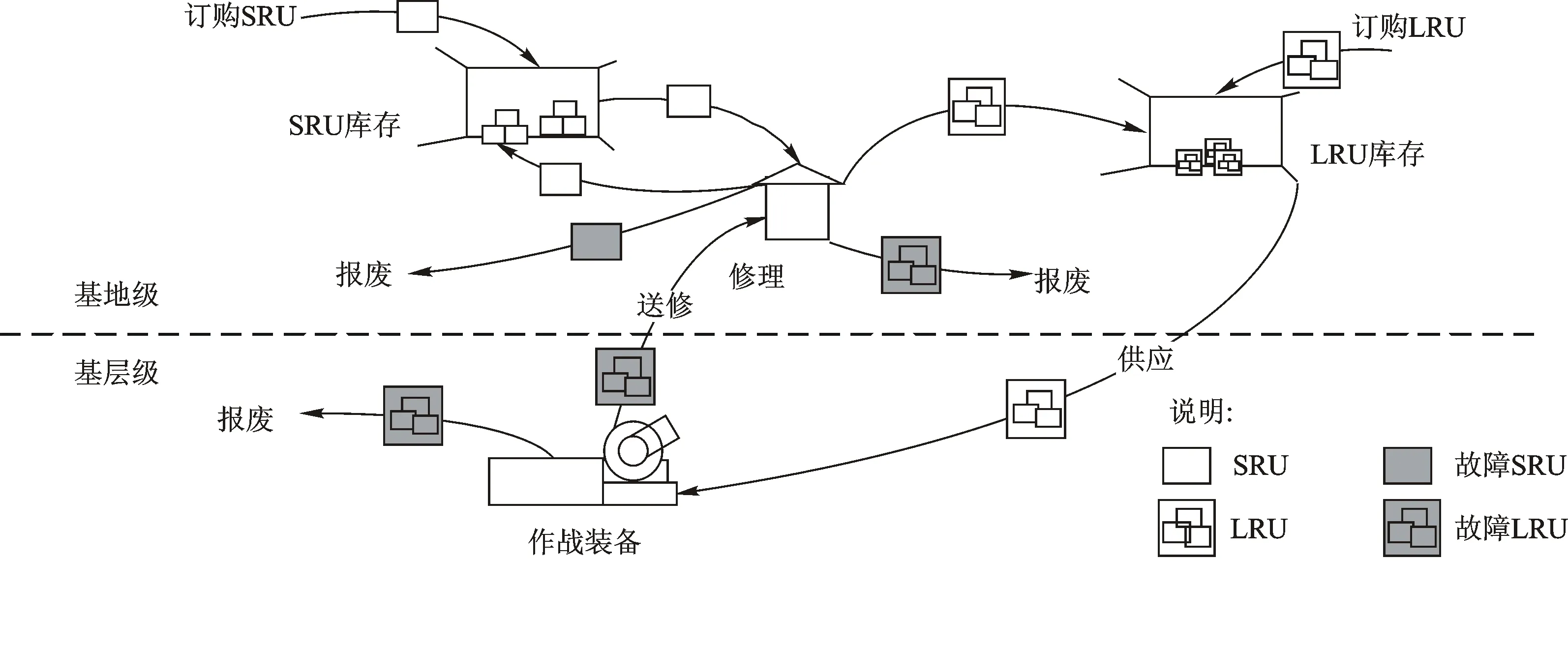
图1 典型的两级备件供应系统示意图

2 备件供应系统SD原理

2.1 备件供应系统因果分析

备件供应系统的功能满足备件需求，备件供应系统根据备件供应完成情况，调整系统控制参数，对供应活动加以控制，是一个典型反馈控制系统[6-7]。通常描述备件供应系统状态的要素有：库存、订货、备件出库、备件故障、备件更换、备件需求、备件供需差额等。备件库存随着订购备件的入库和备件的出库发生变化，出库使库存减少，入库使库存增加；换件维修时，备件故障需要进行更换的速率受制于备件供应速率，当备件供应充足时，故障备件可以得到及时的更换，减少了备件需求的积累；若备件供应不足，则故障备件无法得到及时更换，从而增加需求量的积累，此时需要提高备件出库速率，以满足备件更换需求，即备件故障需求率的增加将引起备件出库率的增加；备件供需差额等于备件需求量减去备件库存量，即备件需求增加引起备件差额增加，库存增加引起备件差额降低。

将库存的出库率作为制定订货率的参考依据之一，同时考虑需求量和供给量的差额信息，与出库率信息一起作为控制订货速率的综合依据。库存的出库速率增大时，需要增加订货率，库存的出库率减小时，相应的减少订货率，从而使库存水平保持稳定。同时，考虑供需矛盾，当需求量大于库存量时，需求供应差值大于零，表明供不应求，应在上一次订货率的基础上增加备件的订货率；反之，减小订货率，最终达到供需平衡，即达到备件的入库率等于备件的出库率。

通过以上分析建立备件供应系统因果关系图，如图2所示。这是典型反馈控制，利用误差来消除误差，从而达到对系统的控制。根据反馈控制原理，在利用误差信息控制系统时，可以通过提高开环增益的方式，提高控制的精度，但是这样就有可能引起系统振荡导致系统不稳定。

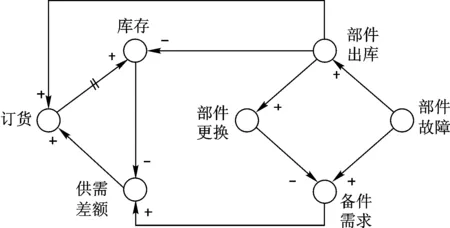
图2 备件供应系统因果关系图

2.2 备件供应系统SD模型

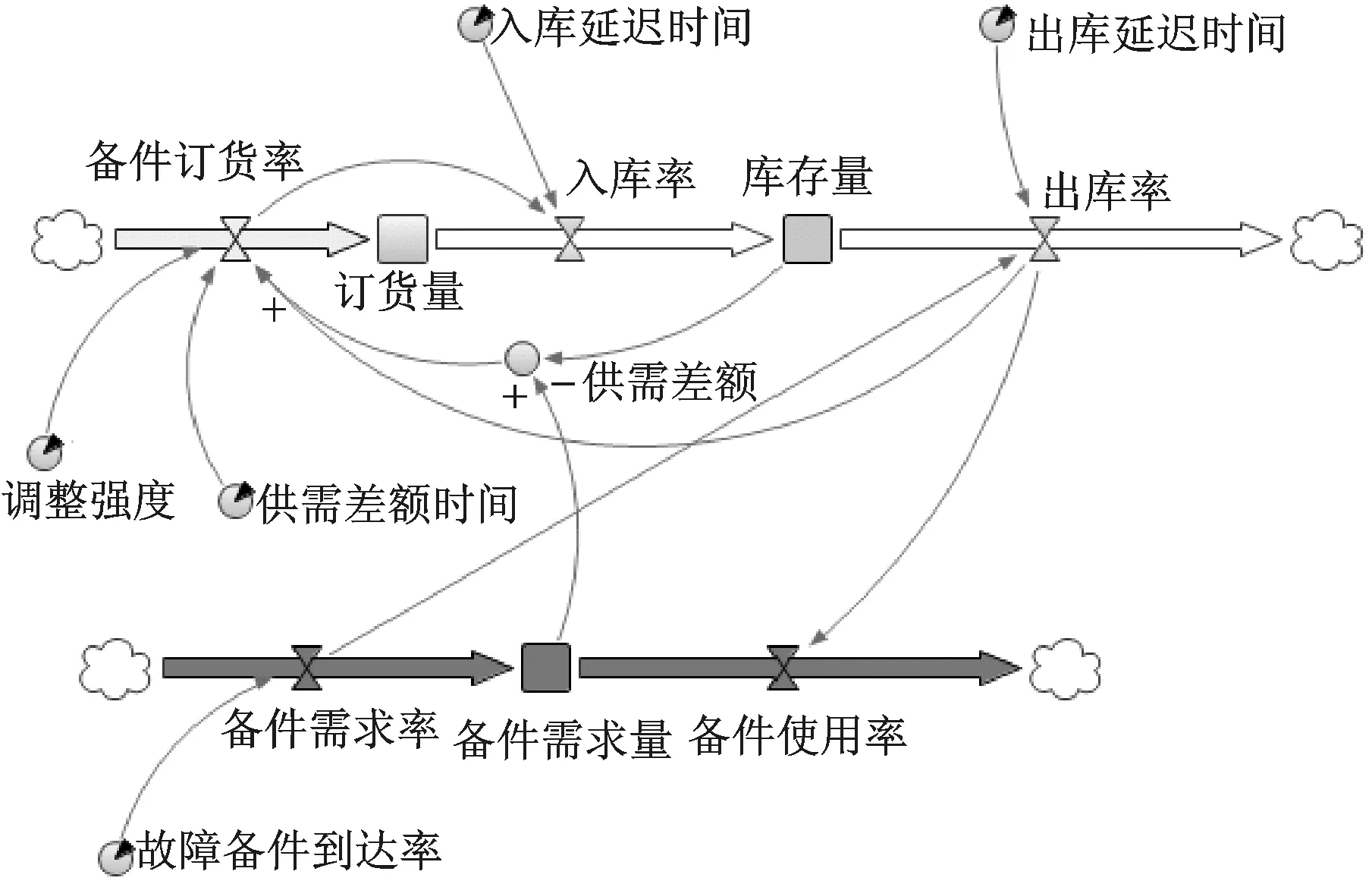
图3 备件供应系统SD模型

根据备件供应系统因果关系图，利用Anylogic建模仿真工具建立备件供应SD流图，如图3所示。SD流图可以更加清晰的刻画图2所示的因果关系，通过建立存量和流速率的数学关系模型，更加具体地反映物质流的结构和反馈的量化关系。同时，加入备件供应环节的延迟信息，可以更加准确的描述备件供应系统的真实情况。

为了建立各个变量间的数学模型方程，定义变量如表1所示。

表1 备件供应系统SD模型参数定义

下面针对各个存量建立系统动力学方程。

对于订货量O(t)，反映在做出订货决策后，备件在运输过程中尚未入库的备件数量，满足

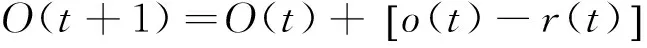
(1)

对于库存量S(t) ，满足

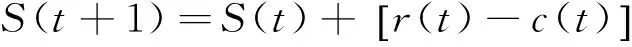
(2)

对需求量D(t)，满足

(3)

考虑入库延迟情况，订货决策到备件入库之间存在物流延迟。所以有

r(t)=o(t-TRK)

(4)

式(4)表示t时刻的入库率等于TRK前的订货率。

初始时刻，装备无故障，正常运行，此时无备件需求，备件需求量D(t)=0，备件需求率d(t)=0，备件出库率c(t)=0，库存S(t)为初始库存状态。当系统发生故障，产生备件需求，即d(t)>0，产生出库率c(t)>0。如果考虑管理等原因产生出库延迟，则有

c(t)=d(t-TCK)

(5)

对换件维修，不考虑换件时间，认为备件出库后直接安装到系统上，则有

u(t)=c(t)

(6)

至此，得到了备件供应系统的基本存量和流速率之间的关系方程。

作为决策者，库存策略和订货策略应该满足一定的备件满足率。科学的思考是，以库存的出库率c(t)为反馈信息决定订货率，以补充库存，保证一定的库存水平。同时，应考察需求量D(t)和库存量S(t)之间的差，即供需差额E(t) ：

E(t)=D(t)-S(t)

(7)

综合考虑出库率c(t) 和供需差额E(t) 信息共同决定是否调整订货率o(t) 。合理的方式是，当E(t)>0时，即需求量大于供给量，供不应求，订货率应在上一周期的出库率基础上有所增加；当E(t)<0，即供过于求，则订货率应在上一周期的出库率基础上有所减少。增加或减少的幅度就是调整强度系数g，调整的方向由E(t)的符号决定，g的作用类似反馈系统的开环增益。即订货率为

o(t)=c(t-1)+g·E(t-TE)

(8)

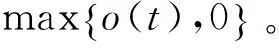
为方便理论分析备件供应系统性能，不考虑各项延迟时间。令TE=0、TRK=0、TCK=0，由式(4)～式(6)和式(8)得到

r(t)=o(t)=u(t)=c(t)=d(t)

(9)

o(t)=c(t-1)+g·E(t)

(10)

将c(t)=d(t)代入式(2)得到

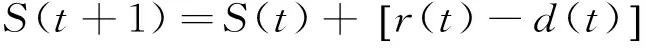
(11)

将u(t)=d(t)代入式(3)得到

D(t+1)=D(t)

(12)

将r(t)=o(t)、u(t)=c(t)和式(7)代入式(10)，并保留含有r(t)和d(t)项，得到

r(t+1)=

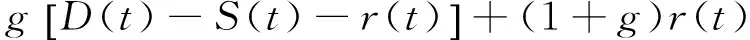
(13)

将式(11)～式(13)写成矩阵形式，得到

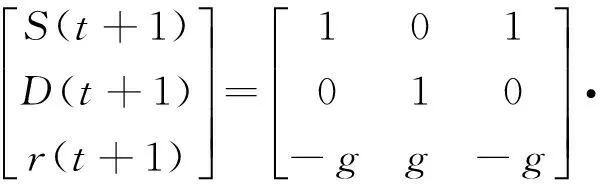
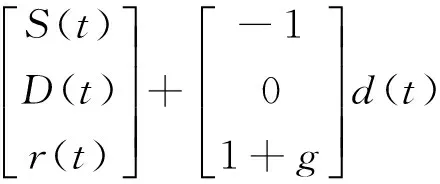
(14)

即得到以备件需求率d(t)作为系统输入，以备件需求量D(t)、入库率r(t)、库存量S(t)为状态空间变量的系统状态空间方程。

该离散系统特征方程为

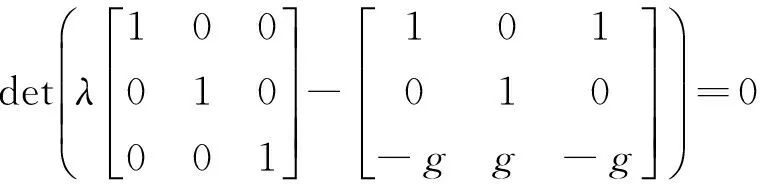
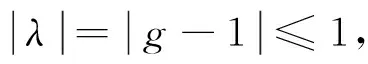
2.3 模型的检验

系统动力学模型的检验包括一致性检验和有效性，主要方法是量纲一致性检验、有效性检验和方程式极端条件检验[8]。

量纲一致性检验——通过分析方程两端变量量纲进行。模型涉及的量纲有存量和速率2类，这里的存量主要是备件的数量，速率主要是单位时间内备件的数量；通过检查，量纲一致。

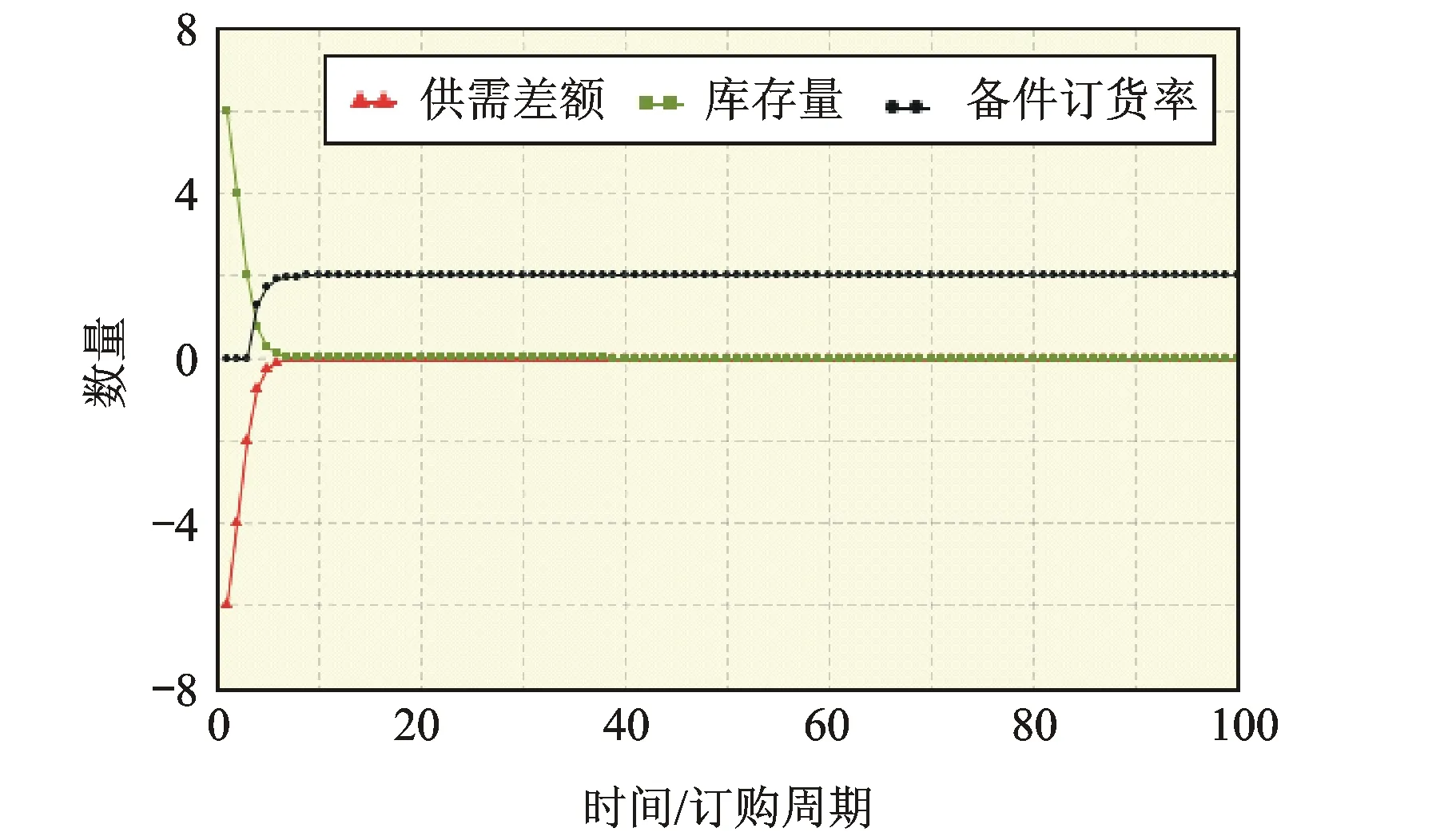
图4 需求率=2时系统行为

方程式极端条件检验——假设备件需求率为0，初始库存量为8，通过仿真得到：库存保持不变，备件订购率为0，与实际情况一致。假设库存为0，备件需求率为4，供应差额调整强度为0，即不考虑供需差额的问题，其他参数均为0，得到仿真结果订购率为4，等于备件的需求率。这与实际情况相符。同样可以逐一检验其他参数的极端条件，均与实际相符。

通过改变备件的需求率，来验证系统的有效性。分别令需求率为2，4，初始库存为8，备件差额调整强度为1(即差多少就在前次基础上多订购多少)，其他参数为0，进行系统仿真。系统开始时备件充足，订购率为0；随着备件的消耗，当库存逐渐减少供不应求时，订购率增加，逐渐达到备件的需求率，如图4和图5所示，这与实际库存情况相符。如果订购策略是按照供需差额的10倍进行，系统仿真结果见如图6所示，这与库存控制模型的理论分析一致[9]，模型通过有效性检验。

图5 需求率=4时系统行为

图6 订购策略g=10的库存变化情况

3 基于备件供应SD模型的计算实验

实验设计(DesignofExperiments，DOE)是一种实验策略，通过有目的的改变一个系统的输入来考察输出改变的情况。结合统计学方法进行实验设计，对实验结果运用统计分析工具加以分析，最大限度的解释分析数据，发现各个因素之间的相互关系，揭示内在规律。在多因素、多水平实验中，如果考察每个因素的每个水平都相互搭配进行全面实验，则实验次数很多，需要耗费大量的实验成本。通常采用正交实验，使用正交表Ln(mk)。式中：n是表的行数，就是实验方案数(实验次数)；k是表的列数，表示实验因素数；m是各个因素的水平数。

3.1 实验设计

假设初始库存量S(t)=6，平均备件需求速率为d(t)=4(件/供应周期)。对于稳定备件供应系统，初始备件库存不影响系统稳态响应，即系统经过一个时期的自我调整，会自发趋于一个稳定的状态，这是具有负反馈闭环系统的特点之一。

针对供需差额调整系数g、供需差额反应时间TE、入库延迟时间TRK和出库延迟时间TCK4个因素，每个因素水平数为3，则使用正交表L9(34)进行。

以供需差额绝对值均值和平均库存量作为考察指标。供需差额的绝对值反映了备件供应系统精确性，值越小表示保障越精确。库存量可以体现库存成本，库存越小库存成本越低，体现了系统的经济性。

平均库存量

式中，N为仿真实验记录的离散时间点数。

供需差额绝对值平均值表示系统绝对误差，它表征了系统精度，是体现“精确保障”的指标。

供需差额绝对值平均值

供需差额反应时间TE、入库延迟时间TRK和出库延迟时间TCK水平选取{0，1，2}，g因素水平取g={0.5，1.0，1.5}。实验方案与系统仿真结果如表2和图7～图10所示。

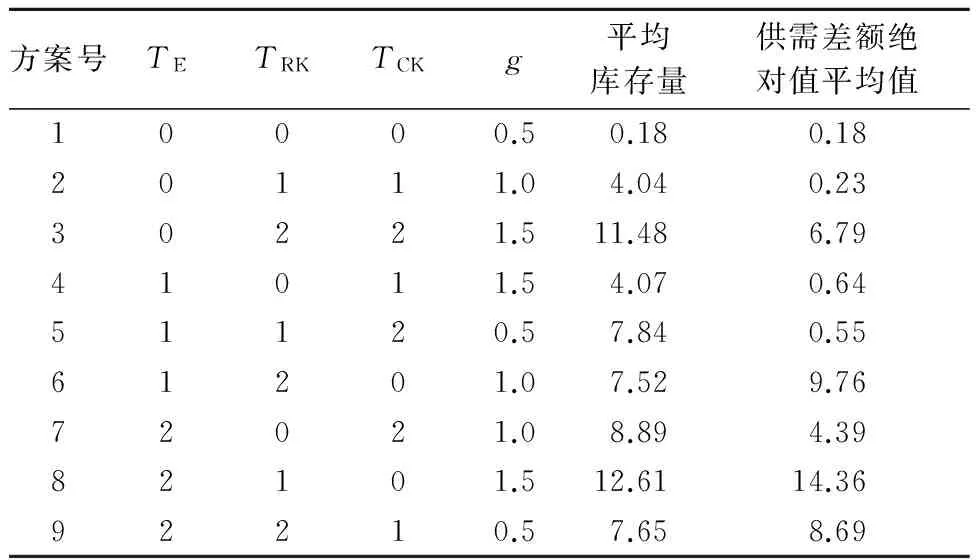
表2 备件供应系统计算实验方案及结果

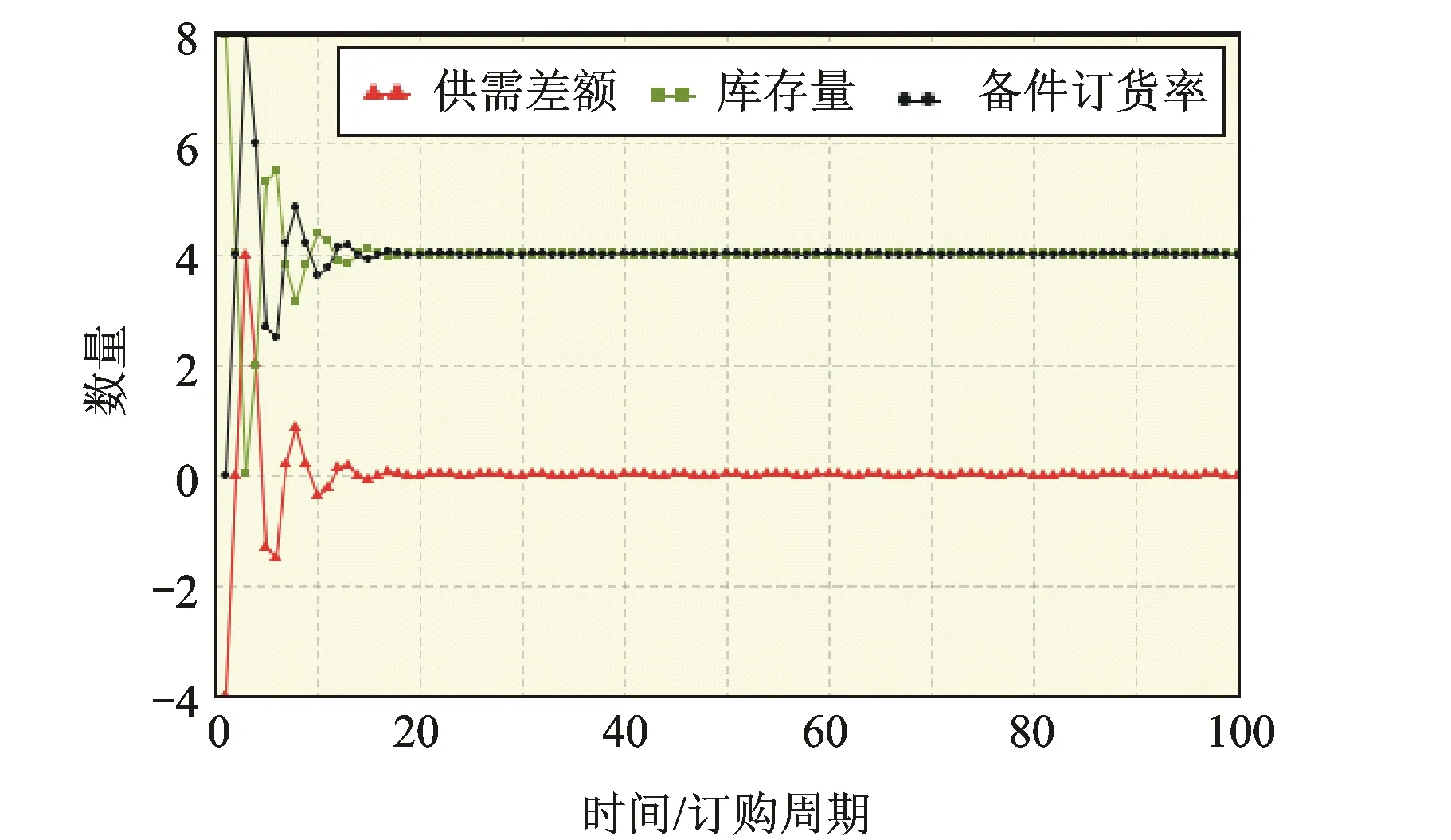
图8 方案2仿真结果

图9 方案4仿真结果

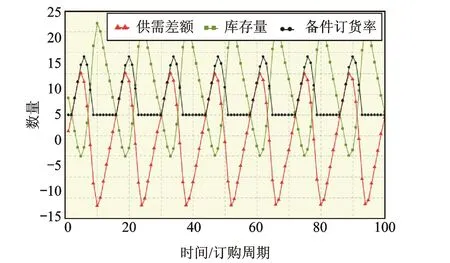
图10 方案6仿真结果

3.2 实验结果与结论

1) 当备件供应系统某些环节(存在较大延迟时，如出库延迟时间、入库延迟时间、供需差额反应时间较大等)，库存水平一直处于波动状态，系统存在不稳定情况(方案3、6、7、8、9)。如供需差额反应时间较大，系统不稳定，说明实际利用的供需关系信息不及时，不能准确反映供需矛盾，导致备件订购策略失效。这表明提高库存管理信息化水平，及时掌握备件供需矛盾，是提高备件供应系统能力的有效手段。

2) 供需差额调整强度系数过大时，系统可能不稳定。说明过分关注备件短缺的历史信息，加大备件订货力度，矫枉过正，导致库存积累(方案3、8)。如某些单位根据出现一次备件短缺的事件，就不顾备件长期以来使用的规律特点，盲目提高备件订购数量，导致订购该备件数量过多，库存积压。

3) 当备件出库没有延迟时，供应系统经过反馈调节，使长期稳定库存水平趋于零，实现零库存供应保障，降低库存成本，提高备件供应效费比。反之，备件出库存在延迟时，会导致备件长期库存水平处于一个稳定值(方案2、4、5)。这个稳定库存水平与出库延迟时间和入库延迟时间之间的差成正比(方案4、5)，出库延迟时间比入库延迟时间大，导致长期库存水平增加(因为总有一部分备件需求迟滞在仓库中，而没有及时发放给备件需求单位)。

4) 由于备件供应环节存在延迟，导致系统不稳定，长期库存水平出现较大波动，且波动幅度逐渐增加。可以通过降低备件供需差额调整强度，降低库存水平波动的幅度，甚至可以使库存水平稳定。说明当物流延迟严重时，可以通过延长订货周期，给基层维修单位一点调整时间，降低库存波动水平。

4 结 束 语

通过备件供应系统SD模型的计算实验，对不同的入库延迟时间、出库延迟时间、供需差额反应时间和供需差额调整强度水平，进行了仿真分析。本文只初步得出了备件供应系统中各个因素对保障效能的影响关系，给出了相关定性结论。在此基础上，还可以进一步在以下方面开展深入研究：(1) 在计算实验基础上，应用定量分析技术进一步分析各影响因素与保障效能之间的相关关系，进行灵敏度分析，探索改进保障能力的途径；(2) 以模型为基础，以备件短缺率和库存量最小化为优化目标，研究备件供应策略优化问题。

References)

[1]丁定浩，陆军，王斌.新型战备完好率模型[J].电子产品可靠性与环境试验.2010,28(3):1-5.

[2]SHERBROOKE C C.Optimal inventory modeling of systems multi-echelon techniques[M].2nd ed.Boston:Kluwer Academic Publisher,2004:20-31.

[3]李阳.基于装备战备完好性的备件配置优化研究[D].成都：电子科技大学,2009:32-40.

[4]杨平律，包磊.不确定需求下多级备件库存系统优化模型[J].指挥控制与仿真.2011,33(6):45-49.

[5]杨平律，包磊.基于METRIC的备件库存优化模型[J].舰船电子工程.2010,30(12):161-164.

[6]田瑾，赵廷弟，刘铮.备件供应系统的动力学原理及动态性研究[J].航空学报.2007,28(5):1104-1109.

[7]宋扬.复杂装备可维修备件供应策略仿真优化研究[D].北京：北京科技大学,2015:55-72.

[8]钟永光，李旭，贾晓菁.系统动力学[M].北京:科学出版社,2009:11-20.

[9]尹大力，颜雁，戚龙.库存控制模型研究[J].长春理工大学学报(自然科学版).2007,30(4):122-124.

(编辑：李江涛)

Research on Computational Experiments of Spare Parts Supply System Based on System Dynamic Model

PAN Xianjun1,2， ZHANG Wei3， ZHAO Tian2， SU Jinbo2

(1. Department of Optical and Electronic Equipment， Equipment Academy, Beijing 101416, China； 2. Department of Graduate Management， Equipment Academy， Beijing 101416， China 3. Department of Equipment Command， Equipment Academy， Beijing 101416， China)

To improve the spare parts supply system efficiency, reduce the spare parts supply cost, and achieve the spare parts supply accuracy, this paper, with the “operation-level to deport-level” support model as its research object, analyses the influence factors of spare parts support ability level of spare parts supply system. It also establishes the operation-level spare parts supply system dynamic model and system dynamic equation, and checks the model to ensure its validity. For the computational experiments, it takes the storage delay time, delivery delay time, supply and demand balance reaction time, supply and demand balance adjustment strength as the experimental factors, and the average inventory and average absolute value of the difference between supply and demand as the object. Experiments show shows that a larger delay time and a larger adjustment intensity of spare parts supply and demand will lead to a larger fluctuation of spare parts inventory level, and a larger time delay will increase the spare parts inventory level significantly.

equipment support; spare parts supply; system dynamics (SD); computational experiments

2017-01-17

国家社会科学基金资助项目(15GJ005-039);全军军事类研究生资助项目(2013JY383)

潘显俊(1980—)，男，讲师，主要研究方向为装备保障管理。panjun_mail@163.com

E92

2095-3828(2017)03-0051-06

A DOI 10.3783/j.issn.2095-3828.2017.03.009