静动力作用下的双排桩加固边坡稳定性分析
2017-07-20何思明李新坡中国科学院山地灾害与地表过程重点实验室四川成都610041中国科学院水利部成都山地灾害与环境研究所四川成都610041
罗 渝,何思明,李新坡(1.中国科学院山地灾害与地表过程重点实验室,四川 成都 610041;2.中国科学院水利部成都山地灾害与环境研究所,四川 成都 610041)
静动力作用下的双排桩加固边坡稳定性分析
罗 渝1,2,何思明1,2,李新坡1,2
(1.中国科学院山地灾害与地表过程重点实验室,四川 成都 610041;2.中国科学院水利部成都山地灾害与环境研究所,四川 成都 610041)
为探讨双排桩结构加固边坡的静动力稳定性,运用极限分析上限定理,在假设前排桩上的土压力为极限土压力,推导出后排桩所需提供抗力的计算公式,同时确定出其最危险滑移面分布。通过双排桩结构加固边坡的算例分析,研究了第二排桩所需提供抗力与双排桩之间间距、第二排桩位置以及地震加速度系数等因素相关关系的一系列研究结果。研究结果表明第二排桩所需提供抗力受双排桩之间间距、第二排桩位置以及地震加速度的影响明显,同时确定出静动力条件下双排桩加固边坡的最危险滑移面分布。
双排桩结构;上限定理;静动力稳定性;加固边坡
0 引言
我国是一个山区面积约占陆地面积2/3的国家,同时我国又位于世界两大地震带——环太平洋地震带和欧亚大陆地震带之间,区域地震十分活跃和频繁。在山区的公路、铁路等基础设施建设中,地形条件的限制使得边坡开挖不可避免,为保证边坡稳定,各种各样的防治结构应运而生。抗滑桩是边坡加固中应用最为常见的结构之一,具有施工方便、组合形式多样、抗滑效果好、投资也不大的优点。在边坡的加固中,双排桩结构得到了广泛应用。然而双排桩加固边坡的理论研究方面,滑坡推力的分配、双排桩间距设置以及前后排桩之间的相互作用影响,以及考虑地震作用的上述问题研究,在国内外学术界都相对欠缺。
在加固边坡的静动力稳定性研究方面,现有的研究方法较多。其中极限分析方法在最近几十年来越来越受到国内外研究学者的关注,具有较多的研究。该方法从能量的角度出发,建立加固边坡的功能平衡关系,进行加固边坡的静动力稳定性问题的求解,能够考虑地震荷载、边坡支护结构的作用。基于这一方法,学者们展开了不同形式抗滑桩加固边坡的静动力稳定性问题研究。Ausilio等[1]以极限分析方法,研究了静动力作用下,抗滑桩加固边坡所需提供的抗滑力,揭示了抗滑桩结构加固边坡的稳定性。罗渝等[2-5]利用极限分析上限定理,结合多块体滑移理论,推导出了静动力作用下抗滑桩、桩板墙、桩锚组合等防治结构加固边坡中不同形式抗滑桩结构所需提供抗力的计算公式以及地震作用下该加固边坡的屈服加速度计算公式,揭示了上述防治结构加固边坡的静动力稳定性。何思明等[6]人则利用极限分析上限定理展开了一系列超前支护桩加固高切坡的静动力稳定性研究。在双排桩加固边坡的静动力稳定性研究方面,何思明,罗渝采取按极限土压力公式设计第一排抗滑桩桩身土压力,基于极限分析的上限定理计算出作用在第二排抗滑桩上的荷载[7]。由此可见,目前在基于极限分析方法的抗滑桩静动力稳定性研究方面,基于单排桩的研究成果较多,对于双排桩这种组合结构加固边坡的静动力稳定研究较为匮乏。同时,文献[7]中虽然是采用极限分析方法展开的双排桩加固边坡问题的研究,但是其研究基于确定的滑移面分布展开,不能够主动的进行潜在最危险滑移面的自动搜索,同时没有考虑地震荷载作用的影响。
因此,本文运用极限分析上限定理,假设前排桩上的土压力为极限土压力,建立静动力作用下后排桩所需提供抗力的计算公式以及加固边坡的屈服加速度计算公式,并确定出双排桩加固边坡的最危险滑移面分布。进而,通过双排桩结构加固边坡的算例分析,研究了第二排桩所需提供抗力与双排桩之间间距、第二排桩位置以及地震加速度系数等因素相关关系的一系列研究结果,揭示双排桩加固边坡的静动力稳定性。
1 前排抗滑桩上的极限土压力计算
对于双排桩结构,前排桩上作用的土压力被假设为极限状态[8-9],可以绕过桩产生塑性流动。Ito & Matsui基于土体塑性变形理论推导了一种计算土体运动作用在桩上的最大水平力的计算公式[8]。
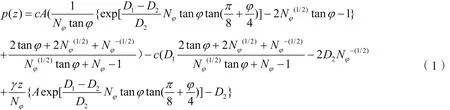
式中, c为土的粘聚力;D1为桩轴线间距;D2为桩的净间距;ϕ为土的内摩擦角;γ为土的容重;z为土层距地表面的深度;Nϕ=tan2(π/4+ϕ/2);A=D(D/D)(N1/2tanϕ+N−1)。
112ϕϕ
对无粘性土,取c=0。
对粘性土, Poulos提出了一种经验解法[10]:

式中,pu为作用于桩上的极限压力和土;
cu为土体的不排水抗剪强度;Np为水平抗力系数,Np=2(1+z/d)≤9,对单桩来说,在地表面处取2,随深度线性增加,到3.5倍桩径(桩宽)或更深处达到最大值9;z为距地表面的深度;d为桩径或桩宽。
对无粘性土中的桩, Broms[11](1964)提出了一个更简单的求解方法:

式中,kp为朗肯被动土压力系数;
p力;a取值3~5。
2 基于极限分析原理的双排桩加固边坡静力稳定性分析
双排桩加固边坡的静力稳定性计算模型如图1所示。假定该加固边坡发生旋转破坏,其潜在滑动面为一对数螺旋面。假设坡体前后缘与旋转中心O连线对水平面的夹角分别为θ0和θh。则该对数螺旋线滑面可表示为:
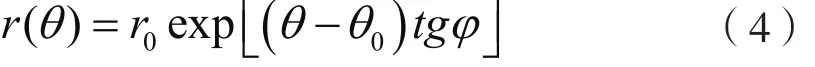
式中,r0为对数螺旋线滑面上与水平面的夹角为θ0时对应的半径;ϕ为坡体材料的内摩擦角。
2.1 外力功率的计算
对双排桩而言,作用在滑体上的外功率主要为滑体重力,滑体自重所做的功率为:
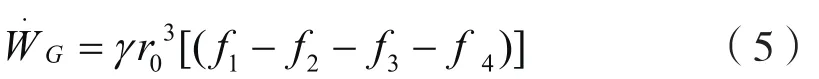
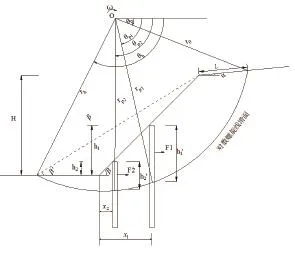
图1 双排桩组合结构计算模型Fig.1 Computation module of double row piles reinforced slope
2.2 滑面上内能耗散的功率计算
对于双排桩而言,发生在滑面上的内能耗散,主要有抗滑桩提供的阻滑力所做的功率和沿滑面上的内能耗散,其计算式分别如下:
(1)沿滑面的内能耗散:
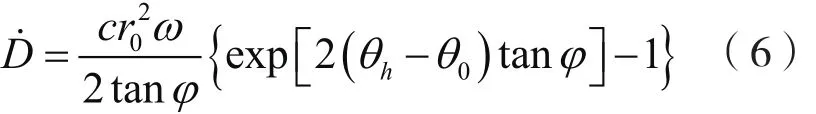
式中,D˙为沿滑动间断面上的能量耗散;c为滑面土体的内聚力;其它符号意义同前。
(2)抗滑桩所做的功率为:
本文假定将处于滑体内部的抗滑桩上半部分的抗力考虑为一个横向的力和一个力矩。因此抗滑桩所做的功率为:
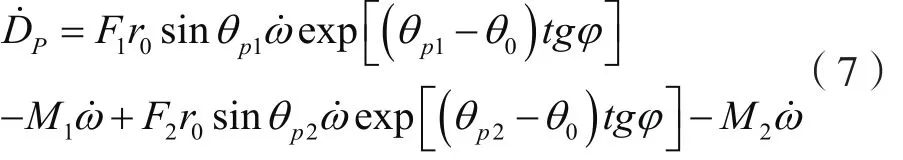
式中,pD˙为抗滑桩所作的功率;F1、F2为单位宽度上两排抗滑桩所提供的抗力;θp1、θp2为抗滑桩所在位置与中心点连线与水平面的夹角;M1、M2为考虑作用在滑面以上部分的抗滑桩抗力分布力的弯矩,如下式:

式中,h1′、h2′为滑面以上部分抗滑桩的长度;m为一系数,本文中抗滑桩滑面以上部分的抗力考虑为线性分布式,m取1/3;其他符号意义同前。
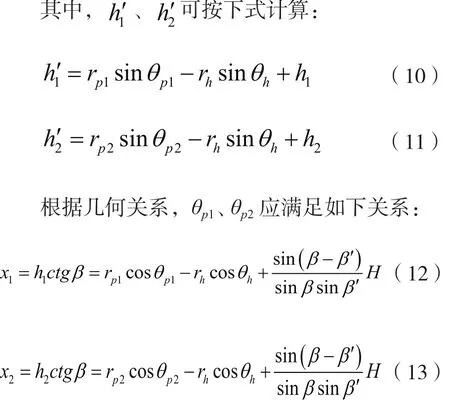
式中,h1、h2为地面以上部分抗滑桩的高度;x1、x2分别为两排抗滑桩距离坡脚的水平距离;H为边坡的高度(图1)。
2.3 坡体稳定性系数定义
根据极限分析上限定理[13],可知坡体的稳定程度取决于外力功与内能耗散的相对关系,故可定义坡体稳定性系数K为:

2.4 双排桩桩身抗力计算
边坡的稳定性,一般由安全系数来确定。当安全系数K≥1时,表明边坡处于稳定状态。根据设计的要求,安全系数是一定的。因此在确定的安全系数下,对于双排桩加固结构,当我们确定第一排抗滑桩的单位宽度抗力F1之后,则可以推求出单位宽度的第二排抗滑桩所需提供的抗力F2。
将上述(4)—(13)式代入(14),整理后得(式中各符号意义同前):
对于式(15),我们假设作用在第一排桩上的土压力为极限土压力,可选取上式(1)—(3)进行求解。再将计算出的F1带入(15)中,进行第二排桩桩身土压力F2的计算。F2为单位宽度的第二排抗滑桩所需提供的抗力,对于第二排有多根桩的情况,则计算每根抗滑桩所需提供的抗力为单宽抗力乘以桩间距。我们知道,在所有可能的滑动面中,越危险的滑面其抗滑桩所需提供的为使边坡达到稳定的抗力值越大。因此,在所有可能的滑面中,最危险滑面就是为使边坡稳定抗滑桩所需提供的抗力最大的滑面。所以,式(15)的求解其实是通过求解F=F(θ0,θh,θp1,θp2,β’)的最大值来找到双排桩结构加固边坡的最危险滑面,而这个值就是为保证边坡稳定第二排抗滑桩所需提供的最小抗力。
通过求解式(16),可求出为保证边坡稳定第二排抗滑桩所需提供的最小抗力值F2,同时未知数θ0,θh,θp1,θp2,β’也可以相应确定出来,得到其最危险潜在滑移面。
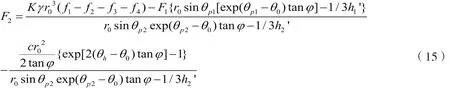

3 基于极限分析原理的双排桩加固边坡动力稳定性分析
3.1 外力功率的计算
参见图2的双排桩加固边坡计算模型。考虑地震作用,双排桩加固边坡,其外力功率除了滑体自重所做的功率外,还有地震荷载所做的功率,其中滑体自重所做的功率同前见式(5)。
地震荷载所做功率为:
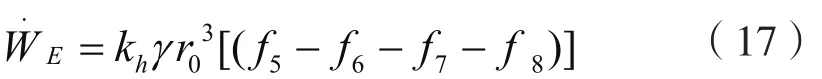
式中,W.E为地震荷载所做功率;kh为地震的加速度系数,kh=a/g;g为重力加速度;其他符号意义同前。f5—f8的具体表达式见附录A(可参考文献[1]、[12])。
3.2 滑面上内能耗散的功率计算
发生在滑面上的内能耗散同前,见式(6)—(13)。
3.3 坡体动力稳定性系数定义
根据极限分析上限定理[13],考虑地震作用,故双排桩结构加固边坡的动力稳定性系数K为:

3.4 双排桩桩身抗力计算
同理,考虑地震荷载作用,在确定的安全系数下,对于双排桩加固结构,当我们确定第一排抗滑桩的单位宽度抗力F1之后,综合上述式(4)—(13)、(17)、(18)则可以推求出单位宽度的第二排抗滑桩所需提供的抗力F2。
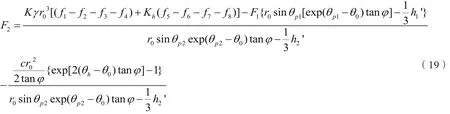
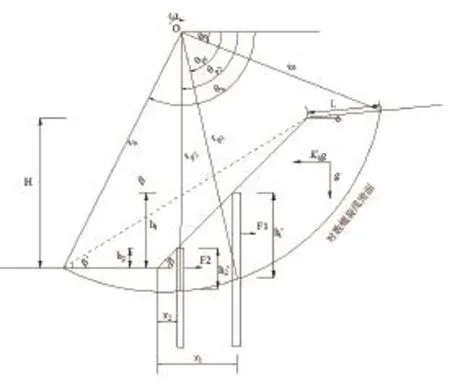
图2 地震作用下双排桩组合结构计算模型Fig.2 Computation module of double row piles composite structure under earthquakes

图3 算例边坡示意图Fig.3 Example for slope reinforced with double row piles
4 算例分析
某边坡拟采用双排桩结构对其进行加固处理,其双排桩的布置如图2所示。边坡坡高H=30m,坡角β=50o,容重γ=20kN/m3,粘聚力c=3.8kPa,内摩擦角φ=16o,第一排桩距坡角距离x1=12m。
在本算例中,第一排桩的桩身土压力假设为极限土压力,可选取极限土压力公式进行求解。将计算后第一排桩的桩身土压力值带入式(15)、(19)求解第二排桩所需提供的最小抗力,如图4—6所示。图4为不同边坡稳定系数(FS=1.0,1.2,1.5)下,第一排桩布置与边坡中部时,为保证边坡稳定第二排抗滑桩所需提供的最小水平抗力值与第二排桩布置位置关系图;图5为在不同双排桩固定间距(dx=10m,dx=15m)情况下,为保证边坡稳定第二排抗滑桩所需提供的最小水平抗力值与第二排桩布置位置关系图;图6为考虑地震荷载作用,不同的地震系数(kh=0.1,0.15,0.2)下,第一排桩布置与边坡中部时,为保证边坡稳定第二排抗滑桩所需提供的最小水平抗力值与第二排桩布置位置关系图。由图1可得:抗滑桩的布置位置取值范围为0—Hcotgβ。这里我们用一个无量纲的参数η来表示第二排抗滑桩所需提供的抗力,/。图7为当第一排桩布置于边坡中部,第二排桩位于x2=1m处时,静力和动力(地震系数kh=0.15)条件下,双排桩结构加固边坡的最危险滑移面分布。
从图4—6可以看出:当第一排桩布置于边坡中部时,不同边坡稳定系数(FS=1.0,1.2,1.5)下,第二排抗滑桩布置位置与其所需提供抗力的分布规律是相同的,随着第二排抗滑桩距边坡坡脚距离x2的增大,其所需提供的抗力有略微增加;当以固定间距布置双排抗滑桩时,随着第二排抗滑桩距边坡坡脚距离x2的增大,其所需提供的抗力呈现先增加再减小再增加的规律。同时当两排桩都位于滑坡体的中下部时,双排桩的间距越大则第二排桩所需提供的抗力越小;不同的地震系数(kh=0.1,0.15,0.2)下,第二排抗滑桩布置位置与其所需提供抗力的分布规律是相同的,同时地震系数越大,第二排抗滑桩所需提供的抗力越大。由此我们可以得出:双排桩在加固边坡时,最佳布置位置应该是在滑坡体的中下部,同时增大两排桩之间的间距。
由图7可以看出:当第一排桩布置于边坡中部时,第二排桩位于x2=1m处,静力条件下,双排桩结构加固边坡的最危险滑移面剪出口位置距坡脚的距离小于地震系数kh=0.15时的滑移面剪出口位置距坡脚的距离;地震作用下滑移面的埋深大于静力条件下滑移面的埋深。
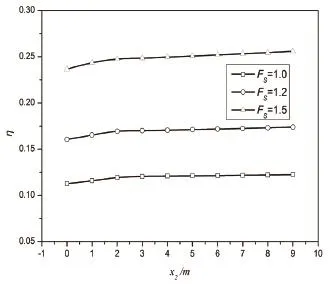
图4 不同边坡稳定系数下,第二排抗滑桩所需提供的水平抗力η与第二排桩布置位置x2关系图Fig.4 The Force η supported by the second row piles against the piles location x2for a slope with different safety factors
5 结论
本文基于极限分析上限定理,假设第一排桩所受土压力为极限土压力,推导出在静动力条件下双排桩结构加固边坡中第二排抗滑桩所需提供的抗力的计算公式。该方法能够简便的计算出后排桩在静动力作用下,为保证边坡稳定桩锚组合结构中抗滑桩所需提供的抗力η,并确定出其最危险滑移面分布。
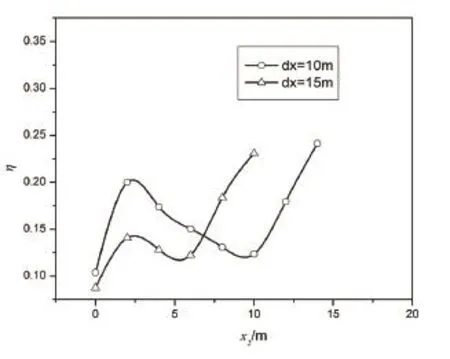
图5 不同固定间距下,第二排抗滑桩所需提供的水平抗力η与第二排桩布置位置x2关系图Fig.5 The Force η supported by the second row piles against the piles location x2for a slope with different double-row piles spaces
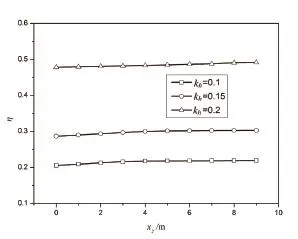
图6 不同的地震系数kh下,第二排抗滑桩所需提供的水平抗力η与第二排桩布置位置x2关系图Fig.6 The Force η supported by the second row piles against the piles location x2for a slope with different seismic coefficient kh
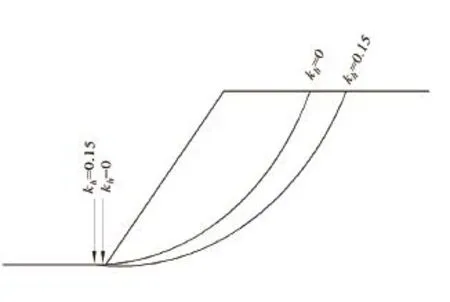
图7 静力和动力(地震系数kh=0.15)条件下,x1=12m,x2=1m时双排桩结构加固边坡的最危险滑移面Fig.7 Potential slip surface of double rowpiles reinforced slope under the static and dynamic condition when x1=12m, x2=1m
通过对实例边坡的计算分析得出:当第一排桩布置于边坡中部时,随着第二排抗滑桩距边坡坡脚距离x2的增大,其所需提供的抗力有略微增加;当以固定间距布置双排抗滑桩时,随着第二排抗滑桩距边坡坡脚距离x2的增大,其所需提供的抗力呈现先增加再减小再增加的规律。同时当两排桩都位于滑坡体的中下部时,双排桩的间距越大则第二排桩所需提供的抗力越小;地震系数越大,第二排抗滑桩所需提供的抗力越大。静力条件下双排桩结构加固边坡的最危险滑移面剪出口位置距坡脚的距离小于动力作用下的滑移面剪出口位置距坡脚的距离;地震作用下滑移面的埋深大于静力条件下滑移面的埋深。
[1] Ausilio E , Conte E, Duente G. Stability analysis of slopes reinforced with piles [J]. Computers and Geotechnics, 2001,28(8): 591-611.
[2]罗渝, 何思明, 欧阳朝军, 等. 地震作用下桩锚组合结构加固边坡稳定性分析[J]. 四川大学学报(工程科学版),2010, 42(supp.): 93-96.
[3]罗渝, 何思明, 吴永. 基于上限定理的桩-锚组合结构设计理论研究[J]. 人民长江, 2010, 41(435):18-20. [4]罗渝, 许强, 何思明, 等. 基于多块体滑移理论的桩板墙结构加固边坡稳定性分析[J]. 西南交通大学学报,2014, 49(6): 967-971.
[5] LUO Yu, XU Qiang, HE Si-ming, et al. A new method to calculate the lateral force acting on stabilizing piles based on multi-wedge translation mechanism[J]. Journal of central south university, 2015, 22(2): 654-661.
[6]何思明, 张晓曦, 欧阳朝军. 超前支护桩加固高切坡的静动力响应与永久位移预测研究[J]. 四川大学学报(工程科学版), 2010, 42(5): 127-133.
[7]何思明,罗渝. 基于上限定理的抗滑群桩设计理论研究[J]. 自然灾害学报, 2010, 19(5): 7-12.
[8] TOMIO Ito,TAMOSSUM. Methods to Estimate Lateral Force Acting on Stabilizing Piles [J]. Soils and Foundation,1975, 15(4): 43-59.
[9] TOMIO Ito. Design Method for the Stabilizing Piles Against Landslide——One Row of Piles[J]. Soils and Foundation,1981, 21(1): 21-37.
[10] Poulos H G . Design of reinforcing piles to increase slope stability[J]. Canadian Geotechnical Journal, 1995, 32(5): 808-818.
[11] Broms B B . Lateral resistance of piles in cohesive soils [J]. Journal of the Soil Mechanics and Foundations Division,1964, 90: 27-63.
[12] Yang Xiao-Li. Seismic displacement of rock slopes with nonlinear hoek-Brown failure criterion[J]. International journal of Rock mechanics & Mining Sciences, 2007, 44(6): 948-953.
[13]陈惠发. 极限分析与土体塑性[M]. 北京: 人民交通出版社, 1995.
Static and Dynamic Analysis on Stability for Double Row Piles Reinforced Slope
Luo Yu1,2, He Si-ming1,2, Li Xin-po1,2
(1. Key laboratory of Mountain Hazards and Surface Process, Chinese Academy of Science, Sichuan Chengdu 610041, China;2. Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Sichuan Chengdu 610041, China)
In order to analyze the static and dynamic stability of a slope reinforce with double row piles, with the assumptions that the soil pressure acting on the first row pile is limit soil pressure, the limit analysis of upper bound method is applied to derived the expressions to calculate the reinforcement force provide by second row piles to prevent failure and the yield acceleration of reinforced slope. And then a case of slope reinforced with double row piles is using to do the static and dynamic stability analysis. Several results of the reinforcement force provided by second row piles versus spacing of distance between two rows of piles, position of the second row pile and seismic acceleration coefficient were obtained in this paper. The result shows that the reinforcement force provided by second row piles is strongly influenced by the distance between two rows of piles, position of the second row pile and seismic acceleration coefficient.
double row piles; upper bound method; static and dynamic stability; reinforced slope
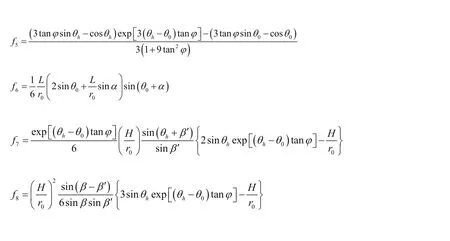
P315.9
A
10.13693/j.cnki.cn21-1573.2017.02.007
1674-8565(2017)02-0037-08
中国科学院STS项目(KFJ-EW-STS-094); 交通运输部科技项目“公路地质灾害多维网络化监测与预警关键技术及示范”(2014364J03090)
2017-01-21
2017-03-05
罗渝(1981-),女,重庆人,毕业于中国科学院大学,博士,助理研究员, 现主要从事滑坡灾害形成机理及防治技术研究方面的工作。E-mail: ly@imde.ac.cn
