一种基于灰度共生矩阵的羊绒与羊毛识别方法

焦明艳

(平顶山神马帘子布发展有限公司，河南 平顶山 467200)

一种基于灰度共生矩阵的羊绒与羊毛识别方法

焦明艳

(平顶山神马帘子布发展有限公司，河南 平顶山 467200)

羊绒和羊毛非常相似，这两种纤维的鉴别一直是纺织工业的难题。经研究，一些学者提出了一种基于灰度共生矩阵的羊绒和羊毛的识别方法。该方法将纤维图像中的鳞片模式看作一种纹理，并使用灰度共生矩阵描述图像中的纹理特征。从每副纤维图像的灰度共生矩阵中提取了5个特征并使用支持向量机作为分类器进行有监督的分类识别。使用澳洲细羊毛和羊绒作为样本进行实验，识别率超过90%，实验证实了该方法的有效性。

羊绒 羊毛 识别 灰度共生矩阵 支持向量机

山羊绒和绵羊毛是两种非常重要的纺织材料，二者外观上非常相似，物理和化学性质也很接近，常常被用于混纺。相比于绵羊毛，山羊绒有更好的柔韧性和光泽，其价格也要比绵羊毛高很多。在企业收购羊绒时要检测羊绒的纯度，羊绒和羊毛的混纺品也要确定二者的比例。在纺织学术界和工业界，羊毛和羊绒的识别都是非常重要的研究内容。学者在这方面进行了很多的研究，早在上个世纪二十年代，Bergen[1]就指出羊绒和羊毛的鳞片的平均高度有所差别，后来又有其他学者将这两种纤维的鳞片厚度、纤维直径/鳞片高度作为识别的依据。但也有学者发现上述几个评价指标都不足以很好地识别羊毛和羊绒[2]。一些学者开始研究几种评价指标的结合，比较著名的有Wortman[3]提出的多指标识别公式，早期的研究多集中于纤维直径及鳞片形态的测量值。还有一些学者开始研究这两种纤维的DNA和蛋白质组成的差别，并借助于检测仪器提出了一些识别方法[4, 5]。随着计算机图像技术的广泛使用，很多学者开始借助于图像技术来研究羊绒和羊毛纤维。石先军等[6]研究了纤维鳞片的十多个指标，并建立贝叶斯模型来识别羊毛和羊绒。马彩霞等[7]测量了纤维的8个特征值，用支持向量机来对两种纤维进行分类。

可以看到，借助于高级的图像技术来识别羊绒和羊毛，是该研究领域的一个重要发展方向。本文使用灰度共生矩阵(Grey Level Co-occurrence Matrix，GLCM)来描述羊毛和羊绒图像，从中分析这两种纤维的差别并进行识别。

1 方法

羊绒的鳞片间隔较大，密度较小，相比而言羊毛鳞片形状更加不规则，鳞片密度较大，鳞片高度小。图1是羊毛和羊绒的光学显微镜图像，放大为400倍。

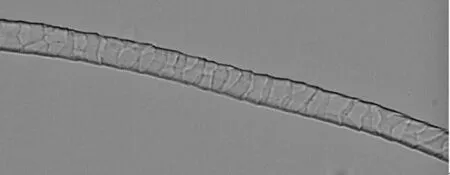
(a)羊毛

(b)羊绒

人们主要是根据羊绒和羊毛纤维表面呈现的鳞片模式来识别它们，而这些鳞片模式可以看作图像中的纹理，本文提取纤维图像中的纹理信息，依据这些信息用以识别这两种纤维。本文首先建立每张纤维图像的灰度共生矩阵，从每个灰度共生矩阵都可以提取表示图像中纹理特征的二阶统计量，然后使用支持向量机(Support Vector Machine, SVM)进行监督学习，从而完成羊毛和羊绒的识别。下面首先介绍灰度共生矩阵的基本概念。

1.1 灰度共生矩阵

灰度共生矩阵由Haralick和Shanmugam[8]最早提出的，该方法计算图像中一定方向和距离两个像素灰度值组成的序数对出现的概率，以此来描述图像中像素的分布规律，有效的一种纹理分析方法[9]。

灰度共生矩阵的本质是像素点对组合而成的联合直方图[10]。这里用I(x,y)表示目标图像，其尺寸为Nx×Ny，灰度级别为Ng，那么就可以定义此图像的灰度共生矩阵为：

P(i,j,d,θ)=#{(x,y),(x+a),(y+b)∈Nx×Ny|f(x,y)=i,f(x+a,y+b)=j} (1)

这里用#(x)来表示集合x中元素数量，P是大小为Ng×Ng的阵。设图像中A像素点(x,y)的像素值为i，图像上另一点B像素点(x+a,y+b)像素值为j，两个像素点A与B之间距离是d，两个像素点间的连线与水平坐标轴的夹角为θ，则a、b与d，θ的关系是a=dcosθ。A、B两个像素点在不同角度和不同距离的灰度共生矩阵，用p(i,j,d,θ)中(i,j)是像素点A与B的灰度值构成的像素对，这样像素点对的组合可以有Ng2个组合。图像中任意两个像素点间的灰度级的空间相关性都可以用灰度共生矩阵来表示，在计算中，常常令θ={0o,45o,90o,135o}，d={1,2,3,4}。下面是灰度共生矩阵定义中的，图像中的像素点的距离与角度的示意图。

图2 灰度共生矩阵像素点的距离和角度示意图

上图中的圆圈表示图像中的像素点，这里表示图像右上角和左下角构成的像素点对的距离与角度示意图。上面已经给出a、b与d、θ的关系，当固定d、θ的值就等于固定a、b的值，使像素点(x,y)在图像I中移动，可以生成不同的像素点对(i,j)，i,j∈[0,Ng-1]。如果变换d和θ，统计图像中的像素点对(i,j)，则生成灰度共生矩阵p(i,j,d,θ)。使用灰度共生矩阵时，往往令d的值为1，然后通过计算θ={0o,45o,90o,135o}4个方向上的灰度共生矩阵得出纹理特征，再求4个方向的特征平均值，这样可以得到旋转不变的特征统计量。

灰度共生矩阵中经常使用的有13个特征统计量，在使用中可以根据实际情况来选取部分特征。通过分析和比较这里使用相关度、熵、角二阶矩、逆差矩以及和方差作为鉴别羊毛和羊绒图像的特征[11]。下面简要介绍一些这几个统计量。

(1)相关度(Correlation)

(2)

这里σ1与u1是P(i)的标准差和均值，这里σ2与u2是P(j)的标准差和均值。如果灰度相关矩阵中的元素值相差不大，同时数值分布均匀，相关度就比较高，这可以用相关度来上描述纹理的方向性。

(2)熵(Entropy)

(3)

熵表示了灰度共生矩阵中元素的随机性的强弱，这可以描述纹理的复杂程度。如果图像没有纹理，则矩阵中元素都是0，那么熵比较小；如果图像纹理杂乱，灰度矩阵中的元素值相差比较大，此时熵值大。

(3)角二阶矩(Angular Second Moment)

(4)

其值为灰度共生矩阵中所有值的平方和的值，角二阶矩用来描述图像纹理的粗细与图像灰度分布均匀度，角二阶距值比较大时表示纹理变化比较规则。

(4)逆差矩(Inverse Difference Moment)

(5)

逆差矩用来描述纹理的同质性，如果图像的像素点对灰度值比较接近，则纹理在图像中不同区域变换比较小，就是是逆差矩比较大。

(5)方差和(Sum of Variance)

(6)

方差和描述图像纹理的周期性强弱，其值是图像中像素点对的变化程度。若图像中纹理的周期性强，则其值越大。

这里取澳洲细羊毛和羊绒纤维各500副光学显微镜图像，灰度共生矩阵的参数θ={0o,45o,90o,135o}，d=5。下面的图3是对样本中的图像计算得到4个统计量的均值,其中图中第1类为羊绒纤维，第2类为羊毛纤维。

(a)相关性

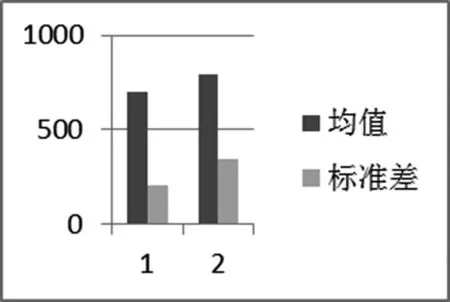
(b)熵

(c) 角二阶矩

(d) 逆差矩

(e)方差和

从上图可以看到羊绒的统计量方差和比羊毛大，这时因为相比而言，羊绒鳞片更有规则，周期性更强。而羊绒其他4个统计量都比羊毛小，这是由于羊毛纤维的鳞片高度较小，鳞片密度较大，并且更加不规则。本文将这5个统计量作为特征，进行羊绒和羊毛纤维的识别。

1.2 图像预处理

由于羊绒和羊毛的图像的对比度不高，并且和有杂质，所以需要在提取特征前先进行预处理，以改善图像的对比度。

(1)图像去燥

在获取羊毛和羊绒的显微镜图像时，灰尘、溶剂和光电转换都可能产生噪声，这些噪声会影响这两种动物纤维的识别，因而在预处理过程中尽量减少噪声。这里使用的是中值滤波对图像进行平滑和去燥。

(2)图像增强

这里使用的是直方图均衡化的方法，直方图均衡化是将图像中比较密集的灰度分布转化为灰度值比较均衡的状况，以此来提高图像的对比度，有利于接下来的特征提取。

1.3 支持向量机

本文使用支持向量机[12]进行监督学习，支持向量机是目前使用最多的分类工具之一，其原理是在高维空间中代表不同类别的向量之间寻找一个超平面，使得各分类之间的间隔最大化，并将该任务转化为凸二次规划问题的求解。

2 实验

将500张羊绒和500张澳洲细羊毛的光学显微镜图像作为样本，从中选取6组不同的比例纤维图像作为数据集。每个数据集随机抽取其中50%作为训练集，另外50%作为测试集。首先对数据集中的图像进行预处理，然后计算每组图像的灰度共生矩阵，接下来提取每个灰度共生矩阵的相关度、熵、角二阶矩、逆矩差和方差和等5个特征值。这5个特征值作为向量，每个向量表示一根羊毛或羊绒纤维，然后将向量作为SVM的输入进行监督学习，每组图像实验进行10次，记录下每组测试集的识别率的平均值，如表1所示：

表1 不同比例训练集的识别率

从表1中可以看到，不同比例下的数据集对识别率影响不大，每组的平均识别率都在90%以上，这也验证该方法的有效性。

3 结论

本文研究了山羊绒和绵羊毛纤维形态上的差别，计算了羊绒和羊毛光学显微镜图像的灰度共生矩阵，并从中提取5个二阶统计量作为特征。以澳洲细羊毛和羊绒为样本，分析和比较了羊毛和羊绒纤维图像这5个特征值。在样本集中选取不同比例的羊绒和羊毛作为数据集，该方法取得了超过90%的识别率，说明了使用这5个特征能够较好识别细羊毛和羊绒。

[1] Von Bergen W. Cashmere[J]. The Melliand,1929, 1(6): 855-859.

[2] Langley KD, Tajr K. The identification of specialty fibers[J]. Textile Research Journal,1981, 51(11): 703-709.

[3] Wortmann FJ, Wortmann G, Arns W. Quantitative fiber mixture analysis by scanning electron microscopy. II. Blends of wool with angora rabbit hair[J]. Textile Research Journal, 1989, 59(2): 73-80.

[4] Zoccola M, Lu N, Mossotti R, Innocenti R, Montarsolo A. Identification of wool, cashmere, yak, and angora rabbit fibers and quantitative determination of wool and cashmere in blend: a near infrared spectroscopy study[J]. Fibers and Polymers, 2013, 14(8): 1283-1289.

[5] Tang M, Zhang W, Zhou H, Fei J, Yang J, Lu W, et al. A real-time PCR method for quantifying mixed cashmere and wool based on hair mitochondrial DNA[J]. Textile Research Journal, 2014, 84(15): 1612-1621.

[6] 石先军. 羊绒特征判析准则及快速识别算法研究[D]. 上海：东华大学, 2011.

[7] 马彩霞, 刘小楠, 刘峰. 绒纤维专家鉴别特征统计分析及自动鉴别方法研究[J]. 毛纺科技, 2014, 42(10): 62-64.

[8] Haralick RM, Shanmugam K, Dinstein IH. Textural Features for Image Classification[J]. systems Man & Cybernetics IEEE Transactions on 1973, smc-3(6): 610-621.

[9] 王杰. 基于颜色和纹理特征的图像检索[D]. 重庆：重庆大学, 2012.

[10]王辉. 基于灰度共生矩阵木材表面纹理模式识别方法的研究[D]. 哈尔滨：东北林业大学, 2007.

[11]袁森林. 基于纹理分析的羊绒羊毛鉴别[D]. 上海：东华大学, 2016.

[12]Vapnik V. The nature of statistical learning theory[J]. Springer science & business media, 2013(1).

2017-04-08

TS 102.3

A

1008-5580(2017)03-0126-04

作者：焦明艳(1985-)，女，助理工程师，研究方向：纺织品设计、纺织图像技术。