EPS转向机主动加载系统研究

王海博，骆艳洁，麦云飞，宋煜霄

(上海理工大学 机械工程学院，上海 200093)



EPS转向机主动加载系统研究

王海博，骆艳洁，麦云飞，宋煜霄

(上海理工大学 机械工程学院，上海 200093)

针对EPS转向机的主动加载实验系统的稳定性进行验证。文中通过对系统主动加载系统各部分进行分析，以阀芯位移为输入量，以马达转动角度为输出量，以干扰力矩为干扰量，利用流体力学的3大方程建立系统模型，进行仿真。得到Simulink仿真的系统阶跃响应图和Bode图，分析发现由阀控液压缸组成的方向盘模拟系统组成的主动加载系统闭环稳定，符合开发要求。

主动加载系统；马达系统； Simulink仿真

汽车安全可靠性关系到用户的生命财产安全，因此，汽车的性能尤为重要[1]。汽车转向系统作为决定汽车安全性的核心要素，是直接影响到车辆性能的关键部件，因此各大车厂都要对转向机进行测试和性能分析[2]。转向机主动加载系统是模拟转向机在实际工作中运动状态时所用的一种加载系统[3]，本文主要完成了转向机主动加载系统的建模与仿真。对主动加载系统的系统结构进行了分析，推导了该系统的传递函数，并对其建立详尽的数学模型，利用Simulink进行仿真，验证该系统的可行性。

1 EPS转向机主动加载系统组成原理

转向机主动加载系统主要通过液压马达进行加载，如图1所示。通常选用阀控液压马达进行加载。阀控液压马达系统是由伺服阀或比例阀构成的闭环系统所得出的，其优点是响应速度较快、结构简单、控制精度好[4]。阀控液压马达系统的组成部分，如图2所示。

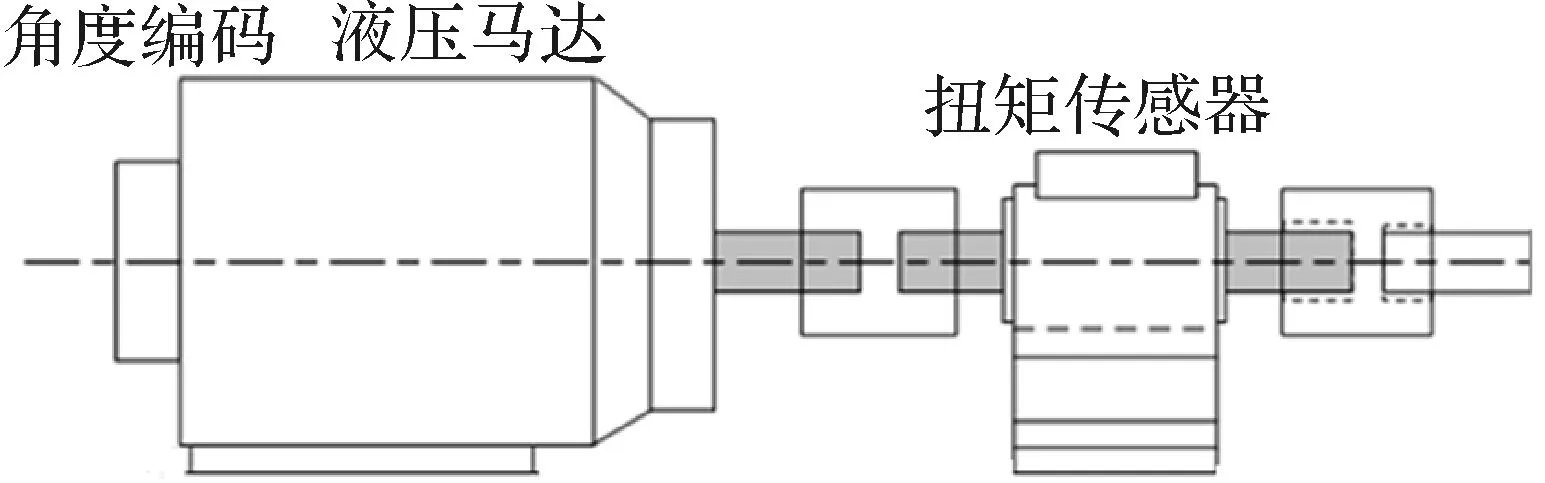
图1 转向机主动加载系统

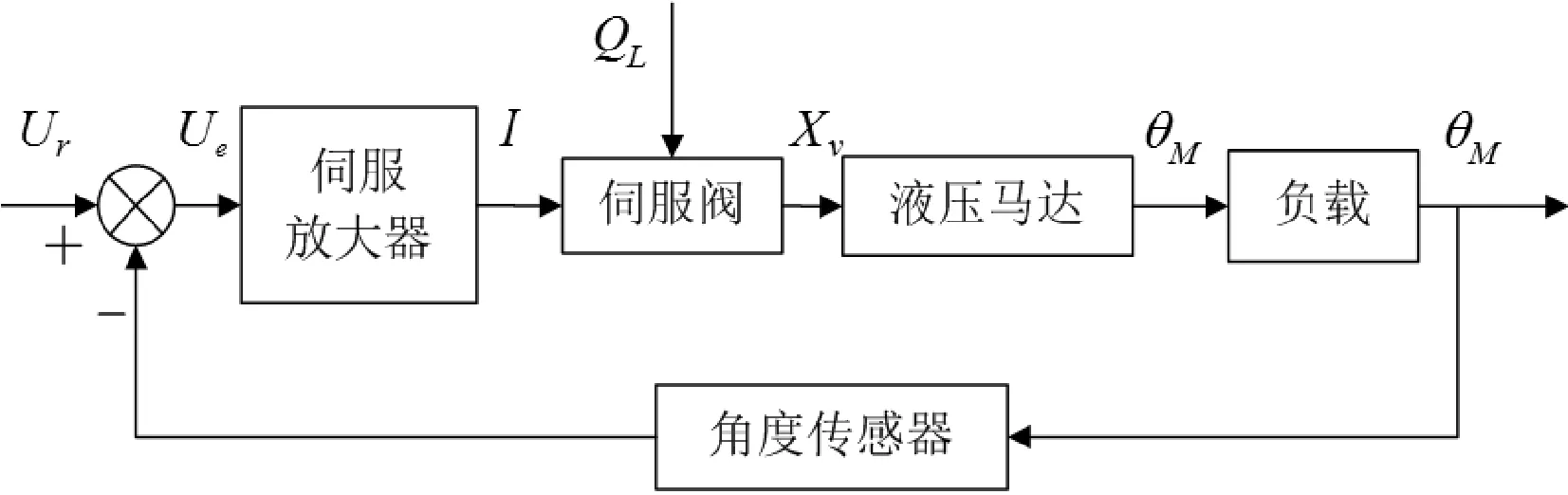
图2 阀控液压马达角度闭环系统结构

2 EPS转向机主动加载系统建模

阀控液压马达角度控制系统，是用伺服阀控制液压马达的流量，从而控制液压马达的转动角度大小的控制系统。该系统由电液伺服阀、液压马达以及其他电液元件组成[5]。

2.1 阀控液压马达系统的基本方程

对于主动加载系统的模型，液压油与负载质量组成的系统可简化为一个质量—弹簧阻尼的二阶振荡系统[6]。主动加载机构的物理模型如图3所示。

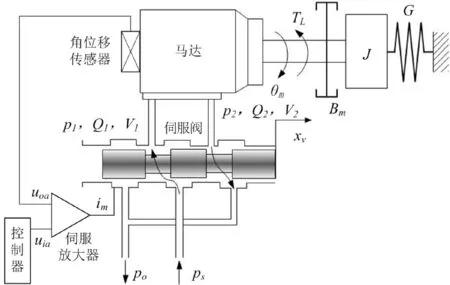
图3 阀控液压马达模型

液压马达的动态特性是指其速度因负载或负载流量瞬态变化而变化的关系，这种变化关系可以用流体力学3大方程描述[7]。

(1)滑阀流量方程

QL=KqXv-KcpL

(1)

(2)液压马达连续性方程。根据流量守恒原理，可压缩流体的连续性方程为

(2)

设V01=V02=V0=Vm/2，即初始时液压马达位于中间位置；并考虑|Dmθ|≪V0，p1+p2=ps=常数，故有

(3)

则

(4)

(3)动力机构力平衡方程。根据牛顿定律，忽略摩擦力等非线性负载及油液质量的影响，由图3可得

(5)

(4)伺服阀模型分析。伺服阀传递函数可看成二阶振荡环节来近似，其数学模型为

(6)

2.2 方框图

将式(1)，式(4)和式(5)，经过拉普拉斯变换可得[8]

QL=KqXv-KcpL

(7)

(8)

(9)

由以上方程可直接绘出阀控液压马达系统方框图，如图4所示。

图4 阀控液压马达系统方框图

2.3 传递函数

根据自动控制理论，运用叠加原理，在列出动力机构传递函数时先分别写出以Xv为输入、以液压马达角位移θm为输出的传递函数，和以干扰力矩TL为输入、以液压马达角位移θm为输出的传递函数，再根据叠加原理写出总的传递函数[9]。

在求以Xv为输入、以液压马达角位移θm为输出的传递函数，令TL=0，根据系统方框图4，可得[10]

(10)

在求以干扰力矩TL为输入、以液压马达角位移θm为输出的传递函数，令Xv=0，根据系统方框图4，可得

(11)

根据叠加原理，得出输入为Xv和TL、输出为液压马达角位移θm的传递函数形式如下

(12)

阀控马达轴的转角对阀芯位移的传递函数为[11]

(13)

3 阀控液压马达角度控制系统

频率特性法是分析和研究液压控制系统最常见的方法之一，频率特性是指线性定常系统在正弦信号作用下，其稳态输出与输入之比与频率的特性函数[12]。频域性能指标主要有：幅值裕度、相位裕度、带宽、相频宽度、谐振频率和谐振峰值[13]。

3.1 系统开环频率特性

频域性能指标主要有：幅频宽(带宽)、相频宽、谐振频率、谐振峰值，还有幅值裕量和相位裕量。频率特性的图形表达常用的有极坐标图和对数坐标图—伯德(Bode)图。将表参数代入主动加载系统开环传递函数，该函数由振荡环节、惯性环节和放大环节组成

(15)

阀控液压马达系统开环频率特性，如图4所示。

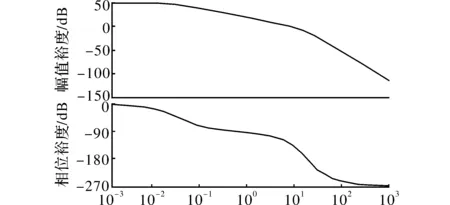
图5 阀控液压马达系统开环频率特性

从图5中可直接得出，系统幅值裕度为Kg= 12.1 dB，相位裕度为γ= 57.3°。根据自动控制设计手册，如果希望系统有良好的控制性能，对相位裕度和幅值裕度的要求分别是：45°≤γ≤70°，Kg>8.0 dB。因此，从系统的频域分析上可以判断出该系统是稳定的，并符合相应的幅值裕度和相位裕度要求。阀控液压马达系统参数，如表1所示。

表1 阀控液压马达系统参数

3.2 系统闭环频率特性

闭环频率特性可以反映控制系统跟踪控制输入信号和抑制干扰信号的能力。控制系统的频带宽度是反映闭环频域性能的重要指标，可由系统闭环伯德图求得带宽频率ωb，频率范围(0,ωb)为系统带宽[14]。阀控马达角度反馈控制系统的闭环传递函数为

(16)

式中，KA为角度编码器系数。

阀控液压马达系统闭环伯德图，如图6所示。

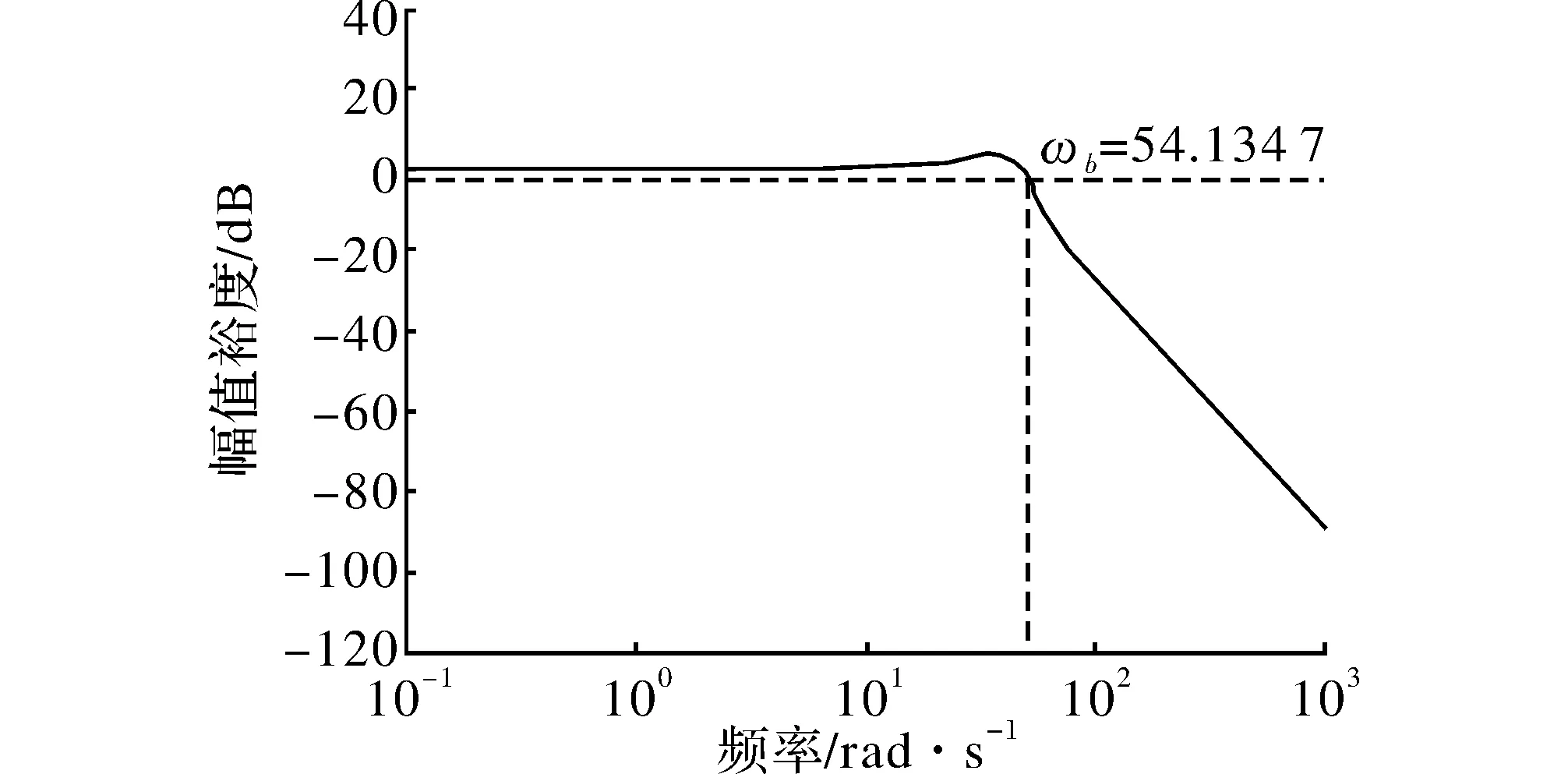
图6 阀控液压马达系统闭环伯德图

由图6可知，系统带宽频率ωb= 54.134 7 rad/s。随着带宽的增大，跟踪控制信号的能力加强，抑制输入端高频干扰的能力减弱。因此系统带宽的选择应折中考虑[15]，阀控液压马达系统带宽大小适中，符合设计要求。

4 结束语

本文通过对EPS转向机主动加载系统的动态数学模型的详细分析，结合主动加载系统中实际运用的控制方法，对这种电液伺服控制系统进行建模与仿真。仿真数据证明，由阀控液压缸组成的方向盘模拟系统频响效果好，符合设计要求。

[1] 刘道东,王铁,高昱,等.汽车整车性能评价方法的研究[J].机械科学与技术,2012,31(3):379-383.

[2] 荆体魁,周雅夫,李驰.汽车电动助力转向系统的初步研究[J].机械制造,2005,43(2):49-50.

[3] 叶涛,郭顺生,杨文凯.汽车电动助力转向系统的初步研究[J].计算机仿真,2004,21(9):160-163.

[4] 李春明.试验机行业发展概述[J].机械工业标准化与质量,2010(2):16-19.

[5] 刘丹丹,骆艳洁,麦云飞.EPS疲劳试验台电液位置系统建模与分析[J].通信电源技术, 2015(5):87-89.

[6] 黎良思,黄义萍,王志翔.模糊控制在液压闭环同步系统中的应用研究[J].电子科技,2015,28(11):147-149,153.

[7] 吴振顺.液压控制系统[M].北京:高等教育出版社,2008.

[8] 胡寿松.自动控制原理[M].北京:科学出版社,2013.

[9] 王春行.液压控制系统[M].北京:机械工业出版社,1999.

[10] 王野牧,杨智超,何松.电液伺服比例综合实验台阀控液压马达控制系统研究[J].机械制造与自动化,2011(3):161-163.

[11] 王春行.液压控制系统[M].北京:机械工业出版社,1999.

[12] 刘佳晨,麦云飞.转向器试验台角度控制液压伺服系统建模与仿真[J].液压气动与密封,2013,32(10):31-34.

[13] 杨叔子,杨克冲.机械工程控制基础[M].武汉:华中科技大学出版社,2009.

[14] 麦云飞,李国妹.液压助力转向器疲劳试验机液压系统建模与分析[J].机械设计,2013, 30(2):86-91.

[15] Luo Yanjie,Li Jiachen,Mai Yunfei.Simulation and inertial force research of three-channel hydraulic loading test bench[C].Switzerland:Application of Mech Mater Vehicle,Mechatronics and Information Technologies,2014.

Research on Active Loading System of EPS Steering Machine

WANG Haibo，LUO Yanjie，MAI Yunfei，SONG Yuxiao

(School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

This paper analyzes the active load test system of EPS steering machine. Through the analysis of each part active loading system, use the spool displacement as input and the motor rotation angle as output, with disturbance torque as disturbances, to establish the system model with three equations of fluid mechanics, to do simulation. Obtained the system step response diagram and Bode diagram of Simulink simulation. The analysis shows that the closed loop stability of the active loading system composed of the valve controlled hydraulic cylinder is composed of the steering wheel simulation system, which meets the requirements of the development.

active loading system; motor system; modeling; Simulink

2016- 10- 25

上海市自然科学基金(12ZR1420700)

王海博(1992-)，男，硕士研究生。研究方向：液压系统等。骆艳洁(1964-)，女，硕士，副教授。研究方向：液压伺服控制系统。

10.16180/j.cnki.issn1007-7820.2017.08.022

TH137

A

1007-7820(2017)08-081-04