一种适用于传递函数模型离散化的M-函数设计
2017-07-19尹湛华
尹湛华
(广东松山职业技术学院电气工程系,广东韶关512126)
一种适用于传递函数模型离散化的M-函数设计
尹湛华
(广东松山职业技术学院电气工程系,广东韶关512126)
针对单输入单输出线性时不变连续系统传递函数模型离散化问题,提出了一种独立于MATLAB控制系统工具箱c2d函数的M-函数设计方法.根据各种常用离散化转换方法的定义及其数学算式,在适当处理传递函数模型中纯滞后部分的基础上,着重运用MATLAB软件的符号计算工具箱函数,编写了具有多分支主控程序结构的实用M-函数离散化程序.最后通过一个具有代表性的算例,验证了该M-函数程序的正确性和有效性,可借以提高设计结果的准确性和置信度.
传递函数模型;离散化方法;MATLAB;程序设计
连续系统离散相似法应用广泛,如何将连续模型转换为离散模型是其首要问题.MATLAB软件在控制工程领域影响甚巨,举凡作者教学过程中所用教材和其他参考文献,只要涉及控制系统计算机辅助设计和仿真分析的连续模型(无论是控制对象还是控制器)离散化问题,几乎都会用到“MATLAB软件控制系统工具箱的c2d函数”.但作者在使用过程中发现该函数并不完善.迄今尚未检索到任何一篇公开讨论该函数应用局限性并提出相应解决办法的文献,因此本文设计了完全独立于c2d函数且能适用于SISO系统连续模型各种常见离散化方法的MATLAB离散化程序.本文设计M-函数程序立足于符号计算功能相对较强的MATLAB7.6.0(R2008a),并在较晚近版本MATLAB8.3.0(R2014a)中测得一致结论.
1 问题描述
MATLAB控制系统工具箱函数c2d的应用局限性主要表现在两个方面.
1.1 离散化方法不全
c2d函数的基本调用格式为sysd=c2d(sysc,Ts,method).其中method用于说明离散化方法,其功能如表1所示(晚近版本MATLAB中method并不包含prewarp选项,而是改用opts选项并借助函数c2dOptions实现).然而,各种差分法(含一阶后向差分、一阶前向差分和中心差分[1]等)也是连续系统模型离散化设计中常用的方法,c2d函数并不包含这些转换方法,这在多种MATLAB论坛中都有反映,说明该函数所提供的离散化方法不尽全面.
1.2 纯滞后环节的近似处理有歧义
在使用c2d函数进行离散化时,若纯滞后时间常数是采样周期的整数倍(可称之为“整步采样”),屏幕输出离散化结果中纯滞后因子指数值即为该整数,各种方法都不会出错.反之,若非整步采样,一方面,采用双线性变换等方法时,程序运行后首先警告称延迟时间被舍入至最接近采样周期Ts,并建议使用ZOH法或FOH法,否则离散化结果是不精确的;另一方面,该函数代码程序中调用了通过Pad é逼近近似处理延迟时间的矩阵指数函数expm,离散化时先将纯滞后时间常数τ分解为整步部分NgTs和余量θ,形如:

表1 c2d函数method的功能选项

式中,Ng为纯滞后因子的指数值(以下简称为“整步系数”),Ts为采样周期.根据MATLAB帮助文档的解释,余量θ将按Pad é逼近近似处理后直接被对象传递函数中的非纯滞后部分吸收,这意味着只要τ<Ts,则必有整步系数Ng=0,但实验证明并非如此.笔者就MATLAB帮助文档中提供的一个实例进行了极限测试,该例所予连续模型的不含纯滞后部分的传递函数表为:

为方便测试,采样周期Ts取1 s,若离散化结果记作Hd,则c2d函数将以参数Hd.inputdelay存储整步系数Ng,编写测试程序代码如下:
clc;close all;clear all;Ts=1;m=0;
Hd=c2d(tf([1-1],[1 4 5],'inputdelay',0.3),Ts,'zoh')
while(Hd.inputdelay==0)
m=m+1;tol=1-10^(-m);
H=tf([1-1],[1 4 5],'inputdelay',tol);
Hd=c2d(H,Ts,'zoh')
end
m,tol=vpa(tol),Hd.inputdelay
e=(1-vpa(tol,12))/1
运行这段程序,结果表明在采用ZOH方法进行离散化时,尽管Hd.inputdelay在连续对象的纯滞后时间常数τ(即程序中的tol)达到10-11截断误差容限之前一直保持为0而未被近似为1,但只要0<τ<Ts,则屏幕返回结果总有整步系数Ng=1.这意味着,只要纯滞后时间常数与采样周期不完全整步,c2d函数ZOH方法的屏幕返回结果就会一律将整步系数Ng=τ/Ts沿正无穷方向取整,这显然与帮助文档的叙述不符;而用类似程序测试FOH方法,则结果与帮助文档的描述基本一致.故这种情况下c2d函数的离散化结果也未足置信.
c2d函数还存在零极点匹配法并非全匹配(即未能实现无穷远处零点的匹配),以及纯滞后部分计算意义不明显等问题,也会给工程应用带来困扰[2].鉴于这些问题,本文设计了一种独立于控制系统工具箱c2d函数,适用于SISO连续系统传递函数模型各种常见离散化方法的M-函数.
2 离散化程序设计
以M-函数文件形式、多分支程序结构,运用MATLAB符号运算工具,在适当处理连续模型纯滞后环节的基础上,从定义出发,遍历各种常用的离散化方法,通过总成得到最终的单输入单输出线性时不变连续系统传递函数模型离散化结果.
2.1 程序首段
采用M-函数文件形式编程,以C2D_for_SISO_LTI_Tf_Model为名定义函数,并用MATLAB的保留字varargin限定可变输入变量使其参数数目介于2个到4个之间,否则报错;输出变量为Sys_d.该函数的调用格式与c2d函数基本一致,默认转换方法也是ZOH.不同之处在于:(1)频率预修正双线性变换法的转折频率ωc既不出现在输入变量列表中,也不是通过其他函数来定义,而是在程序执行过程中从键盘输入.(2)纯滞后环节的近似处理方式不同,第4个输入变量appx用于选择纯滞后环节的近似处理方法.
2.2 纯滞后环节预处理程序段
设连续系统传递函数模型为G(s).程序开始时,先将G(s)分解成不含纯滞后部分Gp(s)和纯滞后环节e-τs两部分,再将纯滞后环节时间常数τ分解为整步部分NgTs和余量θ,即:
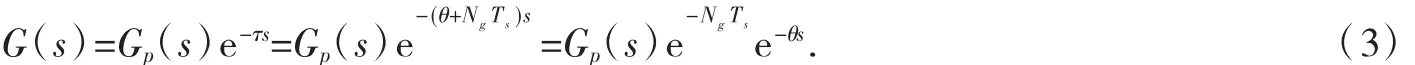
进而可得纯滞后环节时间常数的整步系数Ng=floor(τ/Ts)和余量θ=τ-NgTs,其中floor(●)表示沿负无穷方向取整,借助MATLAB函数floor实现.在程序总成段,整步部分z-Ng将作为因子直接代入最终的离散化结果中;而剩余部分e-θs则根据实际情况,采用Pad é逼近(缺省时,利用MATLAB函数pade实现)、1阶Taylor逼近(当θ<<Ts时)或全极点逼近(当θ接近Ts时)进行近似处理得Gd(s)[3-5],然后与不含纯滞后部分Gp(s)相乘将其吸收,得:

离散化方法为零极点匹配法时采用1阶Pad é逼近,否则缺省情况下一概采用3阶Padé逼近,如表2所示.该段程序核心代码如下:
tol=sys_c.inputdelay;
[num_gps,den_gps]=tfdata(sys_c,'v');
syms s z t k;
Ng=floor(tol/Ts);%整步系数
theta=tol-Ng*Ts;%非整步部分时间余量
if theta~=0
switch appx
case{'taylor','taylo','tayl','tay','ta','t'}
gds=vpa(simplify(1-theta*s));%1阶Taylor逼近
case{'allp','all','al','a'}
gds=expand(simplify(1/(1+theta*s+0.5*theta^2*s^2)));%全极点逼近
otherwise
switch method
case{'matched','matche','match','matc','mat','ma','m'}
[num_gd,den_gd]=pade(theta,1);%1阶Pade逼近
otherwise
[num_gd,den_gd]=pade(theta,3);%3阶Pade逼近
end
gds=expand(simplify(poly2sym(num_gd,'s')/poly2sym(den_gd,'s')));
end
else
gds=1;
end
g0s=simplify((poly2sym(num_gps,'s')/poly2sym(den_gps,'s'))*gds);
2.3 公式法直接转换程序段
对于前向差分法、后向差分法、中心差分法[1,6]、双线性变换法和频率预修正的改进双线性变换法,可直接套用表3中连续域算子s到离散域算子z的转换公式,利用符号计算工具箱复合函数compose直接代入G0(s)进行符号运算即可得到G0(z).该程序段核心代码如下:
switch method

表2 纯滞后环节时间常数的非整步余量θ近似处理方法
case{'bwd','bw','bd','b'}
s=((1-z^(-1))/Ts);%后向差分法
case{'fwd','fw','fd'}
s=(1-z^(-1))/Ts/(z^(-1));%前向差分法
case{'ctd','ct','cd','c'}
s=(1-z^(-2))/Ts/2/z^(-1);%中心差分法
case{'tustin','t','tu','tus','tust','tusti','tst','tt'}
s=2*(1-z^(-1))/Ts/(1+z^(-1));%双线性变换法
case{'prewarp','pre','prew','prewa','prewar','pp','pw','pwp','prwp','p'}
wc=input('Please input the critical frequency Wc(in rad/sec) wc=');
s=wc*(1-z^(-1))/(1+z^(-1))/tan(Ts*wc/2);%改进的双线性变换法
end
gpz=compose(g0s,s);%用符号函数复合工具compose代入
2.4 零极点匹配法程序段
根据定义,零极点匹配法不但要分别进行零点和极点全匹配,还要进行稳态增益匹配.因此,实际编程时还包括用多项式求根函数roots解得连续系统传递函数的零点和极点、通过公式实现从s域到z域的映射并用for循环实现分子因式和分母因式连乘,以及匹配稳态增益等3个步骤,实际设计程序时,零点和极点全匹配应使用:


表3 公式法直接转换的部分常用离散化方法
其中zi(i=1,2,...,m)表示零点,pj(j=1,2,...,n)表示极点;而稳态增益匹配用:

实验表明,MATLAB控制系统工具箱c2d函数的'matched'方法不是全匹配,未能实现无穷远处零点的匹配,离散化结果中并不包含(z+1)n-m因子,进而稳态增益匹配结果也将有所不同.该程序段核心代码如下:
[num,den]=numden(g0s);
g0s_num=sym2poly(num);
g0s_den=sym2poly(den);
zero=roots(g0s_num);%求连续传函的零点
pole=roots(g0s_den);%求连续传函的极点
%符号计算进行零极点匹配
gps0=compose(g0s,0);
m=length(zero);
n=length(pole);
gpz_num=1;gpz_den=1;
if m>=1
for i=1∶m
gpz_num=gpz_num*(z-exp(zero(i)*Ts));
end
end
if n>=1
for j=1∶n
gpz_den=gpz_den*(z-exp(pole(j)*Ts));
end
end
gpz=vpa((z+1)^(n-m)*gpz_num/gpz_den);%包含无穷远处零点的完全匹配
gpz0=compose(gpz,1);
kz=gps0/gpz0;%匹配稳态增益gpz=kz*gpz;
2.5 常用加保持器离散化方法程序段
对于脉冲响应不变法、加零阶保持器法、加一阶保持器法以及加三角形保持器法[7-8],需根据变换方法的不同做一些特殊处理:因为e-sTs=z-1,故先可将各种保持器模型中有关e-sTs部分分离出来得Gm(z),然后将其余部分直接与G0(s)合并为Gp(s)再做处理,方法见表4.具体编程步骤可归纳为:(1)通过拉普拉斯反变换函数ilaplace将表4中的Gp(s)转换为连续时域信号gp(t).(2)用符号工具箱复合函数compose将gp(t)离散化为脉冲序列gp(k).(3)用Z变换函数ztrans将gp(k)变换为gp(z),进而得Gp(z)=gp(z)Gm(z).
MATLAB控制系统工具箱函数c2d并不包含严格意义上的“加一阶保持器法”,其FOH方法实际上对应于表4中的“加三角形保持器法”[9].该程序段核心代码略.
2.6 离散化结果总成程序段
在求得Gp(z)的基础上,可得离散化结果的符号表达式为:

再经MATLAB函数sym2poly将符号表达式转换为最终的离散模型脉冲传递函数.

表4 各种加保持器离散化方法的特殊处理
3 算例
设某带时间延迟一阶模型(First-Order Lag Plus Delay,FOLPD)的传递函数为G(s)=e-1.5s/(4s+1)[10],采样周期分别选取Ts=0.5 s和Ts=1 s,依次采用MATLAB固有控制系统工具箱函数c2d和按本文方法设计的离散化M-函数C2D_for_SISO_LTI_Tf_Model遍历各种离散化方法进行转换.为便于比较,后者关于纯滞后环节的余量近似处理方法均为缺省,即全部按Padé逼近方法处理.算例检验结果如表5所示.

表5 屏幕输出算例离散化结果
当采样周期选取Ts=0.5 s时,除零极点匹配法之外,MATLAB软件固有函数c2d和本文M-函数C2D_for_SISO_LTI_Tf_Model对应离散化方法的执行结果并无不同,表明二者在整步采样的情况下是等效的;但当采样周期选取Ts=1秒时,结果则出现明显差异.由于本文所采用的离散化转换方法都是从严格的定义出发的,结果更可信.另外,前向差分法、后向差分法、中心差分法和加一阶保持器法亦已在C2D_for_SISO_LTI_Tf_Model中全部呈现,而这些方法无法通过c2d函数实现.
4 结语
面向控制系统工程设计和仿真分析中常见的连续模型转换为离散模型问题,本文设计了一种独立于MATLAB控制系统工具箱c2d函数的M-函数离散化程序.该函数在采用适当方法近似处理单输入单输出连续定常系统传递函数模型纯滞后环节时间常数的基础上,借助MATLAB软件的符号计算工具,从定义出发以多分支程序结构涵盖多种常用离散化转换方法,然后通过总成从计算机屏幕返回最终离散化结果.典型算例表明,使用该M-函数可以有效解决c2d函数所固有的方法不足以及算法歧义等问题,能够提高离散化结果的准确性和置信度,具有实用意义.
[1]张东峰,惠晶,许胜.基于中心差分法的光伏阵列最大功率点跟踪[J].电力电子技术,2012,46(9):10-12.
[2]尹湛华.Dahlin数字控制器的两种MATLAB辅助解法[J].南方金属,2013,(4):53-55,60.
[3]薛定宇.控制系统计算机辅助设计——MATLAB语言与应用[M].2版.北京:清华大学出版社,2006.
[4]尹先斌,周有训.基于Taylor和Padé逼近的滞后系统IMC-PID研究[J].昆明理工大学学报(理工版),2006,31(2):76-81.
[5]靳其兵,刘明鑫,冯春蕾.大滞后特性处理的研究和比较[J].北京化工大学学报(自然科学版),2008,35(6):98-101.
[6]王倩颖,吴斌,欧进萍.考虑作动器时滞及其补偿的实时子结构实验稳定性分析[J].工程力学,2007,24(2):9-14,8.
[7]喻娅娅,王印松,许鹏春.数字控制中的保持器与系统稳定性的关系[J].自动化技术与应用,2004,23(11):17-19.
[8]卢志强.连续时间系统课程的离散化方法综述[J].中国科教创新导刊,2010(34):85-86.
[9]张绍宁,戴红缨.MATLAB在数字控制系统设计中的两则应用问题[J].计算机仿真,2003(Z1):203-205.
[10]陈雪梅,王萍.达林算法在z域和δ域的仿真[J].天津工业大学学报,2004,23(1):73-75.
The Design of A M-function Applying to Transfer Function Model Discretization
YIN Zhan-hua
(Department of Electrical Engineering,Guangdong Songshan Polytechnic College,Shaoguan 512126,Guangdong,China)
For the discretization of transfer function model of SISO-LTI continuous systems,the design method is proposed about a M-function which is independent of the C2D function of MATLAB control system Toolbox. According to the definition and mathematical formulas of a variety of common discretization methods,the practical discretization program of the M-function with multi-branch master control structure is coded mostly by the symbolic Toolbox functions of MATLAB software and properly based on preconditioning the time delay part of the transfer function model.Finally,the correctness and validity of the M-function is verified by a typical example which thereby can improve the accuracy and confidence relating to the designing results.
transfer function model;discretization methods;MATLAB;program designing
N945.12
A
1007-5348(2017)06-0004-07
(责任编辑:邵晓军)
2017-02-19
尹湛华(1969-),男,内蒙古赤峰人,广东松山职业技术学院电气工程系副教授,硕士;研究方向:计算机测控技术.
