高压下L10-FePd晶态合金的物性研究

禹国梁， 成泰民， 张 辉， 徐 策

(沈阳化工大学 材料科学与工程学院， 辽宁 沈阳 110142)

高压下L10-FePd晶态合金的物性研究

禹国梁， 成泰民， 张 辉， 徐 策

(沈阳化工大学 材料科学与工程学院， 辽宁 沈阳 110142)

采用基于密度泛函理论(DFT)的第一性原理平面波的方法，结合广义梯度(GGA)近似计算了高压下四方相L10-FePd晶态合金的结构稳定性、晶格常数、焓差、磁性及电子态密度.计算得出压力小于170 GPa时，考虑磁性的体系比不考虑磁性的体系更稳定，呈铁磁态合金,L10-FePd晶态合金的磁矩随着压力的增大不断减小；当压力大于170 GPa时，考虑磁性的体系与不考虑磁性的体系的焓基本相同，且体系的铁磁性消失，电子极化态密度趋于对称.因此，L10-FePd铁磁性合金的铁磁性坍塌临界压力处于170 GPa附近.

高压； L10-FePd晶态合金； 铁磁性坍塌临界压力； 电子态密度

Fe-Pd合金体系存在不同的磁性相，其中铁磁性形状记忆合金广泛应用于多功能材料，具有广阔的应用前景，例如由于大的磁场诱导应变可用于磁传感器、磁热弹性元件[1].具有很高单轴磁晶各向异性和很大矫顽力的四方有序相L10-FePd铁磁性合金(在300 K下，单轴磁晶各向异性能KU=1.7×106J/m3)作为超高密度磁记录介质材料在电子信息产业有着非常广泛的应用前景[2].从实用角度而言，磁记录材料还需要有较低的有序-无序相变温度和较弱的晶间交换耦合作用，这有利于在制备和生产过程中对材料晶粒粒径大小的控制和提高记录信息读取的准确性.Kelly P E 等[3]利用超导量子干涉仪(SQUID)对 [Fe(10Å)/Pd(12Å)]10合金的磁性进行了测量，呈现无序-有序中间态的面心立方相，且其矫顽力较小，表现为软磁相.由于Pd的Stoner因子很大(S=10)，称为“近铁磁性金属”.Pd与铁磁性金属形成合金时有许多异常现象[4]，Fe1-xPdx合金的磁性强烈地依赖于其结构以及Pd的相对含量，文献[5]利用第一性原理计算了不同配比下的Pd含量对基态磁性及电子结构的变化规律.但是，在高压下对四方有序相L10-FePd铁磁性合金的磁性及电子结构的计算鲜有报道，为此，我们对具有超高密度磁记录性能的L10-FePd铁磁性合金的物性随压力的变化规律进行了系统的研究，这为实验工作者提供了理论依据.

1 计算方法与模型

计算采用了基于密度泛函理论平面波赝势方法的VASP[6-8]程序.电子间的交换关联作用选择基于广义梯度近似(GGA) 的perdew-burke-ernzerhof (PBE)[9]形式，离子实和价电子之间的相互作用采用投影缀加平面波[10](PAW)方法计算，Fe 原子的3p63d74s1和Pd原子的4p65s14d9作为价电子处理.布里渊区积分采用monkhorst-pack方法对布里渊区进行采样，积分网格为12×12×12，平面波基函数的截断能量取为500 eV.对原子的弛豫采用一阶的methfessel-paxton smearing方法，smearing展宽为0.2 eV，总能的计算采用了BLÖCHL[11]修正的线性四面体方法以获得更高的精度.电子和离子弛豫的自洽收敛标准分别为能量小于1.0×10-6eV和1.0×10-4eV.

L10-FePd晶胞结构如图1所示.

图1 L10-FePd晶胞结构

2 结果与讨论

2.1 结构优化

表1列出了L10-FePd晶态合金的结构优化后的晶格参数和原子磁矩.本文采用PBE近似下结构优化得到的理论晶格参数均与实验文献[13]和理论文献[14]符合的较好，说明我们所采用的计算方法和结果非常可靠.

表1 结构优化后L10-FePd的晶格参数与文献报道的实验值及计算值的比较

2.2 压力对FePd晶格常数的影响

图2给出了L10-FePd晶态合金的晶格常数与晶胞相对体积随压力的变化关系.

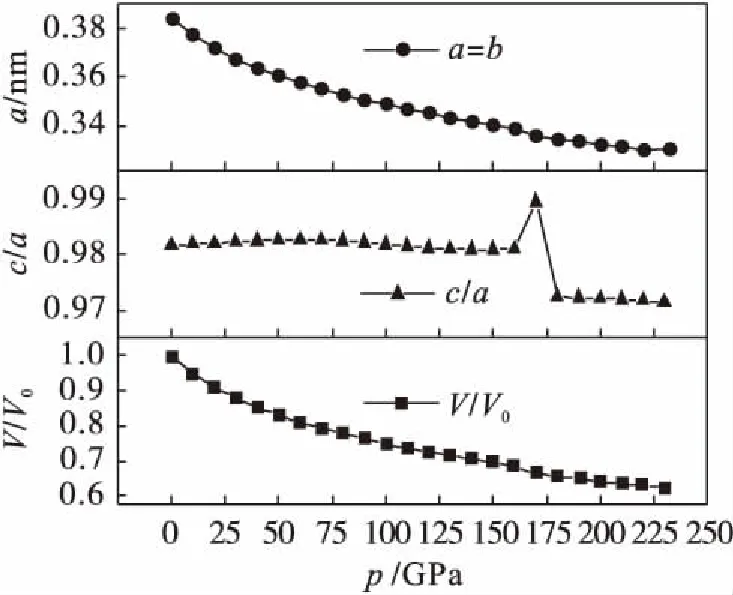
图2 L10-FePd合金在不同压力下的晶格常数和相对晶胞体积

图2中V0是零压下 L10-FePd 晶态合金的晶胞体积.从图2中可以看出:随着压力的增大，晶格常数a逐渐变小，c/a变化幅度比较小，说明晶格常数c随着压力的增大也随之逐渐变小，因而总体上体积V随着压力的增大不断的减小，从相对体积V/V0曲线也可以看出体系的体积不断减小.这是因为L10-FePd合金在外界压力的作用下，改变了原子间的相互作用力，被压缩的晶体原子间的键长变短.从图2中c/a曲线可以看出c/a≈0.98，这说明该合金体系近似为立方结构.在外界某种条件下可能会激发出新的滑移系，对材料的延展性有较大的提高，曾有报道有序四方相L10-FePd合金转变为无序立方相合金[12，15].此外，从相对体积V/V0曲线可以看出随着压力的增大，该曲线为“上凸形”，说明相对体积的变化率逐渐变小，从而说明随着压力的增大，体系对压力的敏感度变低，即不容易被压缩.但是压力在160～170 GPa区间晶胞的c/a变化明显，导致了晶胞体积急剧减小，这与体系的磁矩在此区间急剧减小、原子间的自旋极化作用急剧消失相对应，说明在此区间Heisenberg交换关联急剧减小.L10-FePd铁磁性合金的铁磁性坍塌临界压力正好处在此压力区间(160～170 GPa).

2.3 高压下FePd合金的焓及磁矩

L10-FePd的焓差和磁矩随压力的变化如图3所示.

(a) 考虑电子自旋极化体系相对于没有考虑电子自旋极化体系的焓差； (b) 不等价原子对体系的磁矩贡献和总磁矩； (c) 不同轨道电子对体系的磁矩贡献和总磁矩

图3 L10-FePd的焓差和磁矩随压力的变化

Fig.3 The enthalpy difference and magnetic moments of L10-FePd changing with pressure

根据焓差曲线[图3(a)]可知：从零压开始对该体系施加压力到170 GPa附近时，考虑电子自旋极化(考虑磁性)的L10-FePd比不考虑电子自旋极化(不考虑磁性)的体系基态结构更稳定，因此，L10-FePd晶态合金是铁磁性合金，这与Yuasa[16]等所报道一致.在施加压力的过程中，这两种体系的焓差逐渐变小，当压力大于170 GPa之后，考虑电子自旋极化的L10-FePd与没有考虑电子自旋极化的体系焓基本相同.从图3(b)和(c)可知：L10-FePd晶态合金的铁磁性坍塌临界压力点在170 GPa附近，体系的总磁矩主要由Fe原子贡献的[见图3(b)]，Pd原子的磁矩在压力小于160 GPa以下几乎不变，而铁原子顶角处的Fe1原子和底心处的Fe2原子线性缓慢减小；但是在160 GPa至170 GPa区间，Pd原子的磁矩明显减小，同时Fe原子的磁矩急剧减小，进而导致体系的磁矩急剧减小.从图3(c)可知：体系的磁矩主要由Fe原子的3d轨道电子和Pd原子的4d轨道电子贡献的，而Fe原子和Pd原子的s(4s和5s)轨道电子与p(3p和4p)轨道电子的贡献是抗磁性的，其贡献明显比Fe原子和Pd原子的d(3d和4d)轨道电子小很多，因此体系显示出铁磁性；当压力大于170 GPa时，体系的磁矩几乎为零，转变为顺磁态，发生了铁磁态到顺磁态的磁性相变.

2.4 高压下FePd合金的电子态密度

由图4(a)可知：常压下P4/mmm结构的有序晶态合金L10-FePd铁磁性主要由顶角处的Fe(Fe1)原子与底心处的Fe(Fe2)原子的3d电子的自旋极化贡献的.低能区体系的电子态密度是Pd原子的4d电子贡献的.对于体系中Pd原子而言，常压下其顺磁性的宏观表现是由Pd原子的4d电子引起的，5s电子与4p电子的贡献是与4d电子的贡献相反，即起抗磁性作用，因为4d电子的贡献大于5s电子与4p电子贡献的总和，体系中的Pd原子表现为顺磁性.从顶角处的Fe1与底心处的Fe2在体系中的电子态密度的贡献可知，其对体系磁矩的贡献几乎等效，这再一次说明L10-FePd铁磁性晶态合金接近于面心立方结构的四方结构，且在费米能级处自旋朝上的电子态密度大于自旋朝下的电子态密度，因此Fe1原子和Fe2原子宏观上表现为铁磁性.在费米能级处电子态密度的贡献主要由Fe原子承担，且费米能级处Pd原子电子态密度较小但不为0，这是良导体的微观表现.随着压力的增大，体系的电子极化越来越小，微观表现为自旋朝上的电子态密度与自旋朝下的电子态密度趋于对称.

由图3和图5可知：压力小于160 GPa时，有序的晶态合金L10-FePd的磁矩随着压力的变化线性缓慢地减小，这是因为在此压力区间Fe1原子与Fe2原子的磁矩变化较小之故，在此压力区间Fe1原子与Fe2原子的自旋朝上与自旋朝下的电子态密度变化较缓慢，但是其峰值向费米能级处移动，所以对体系的磁矩而言变化较缓慢；压力大于170 GPa时，体系的磁矩急剧减小，微观表现为体系中Fe1原子与Fe2原子的电子态密度急剧趋于对称，从而电子自旋极化急剧减小，导致了体系的铁磁性坍塌，这说明P4/mmm结构的L10-FePd晶态合金的铁磁性坍塌临界压力处在170 GPa附近.

图4 0～100 GPa压力下L10-FePd的电子态密度

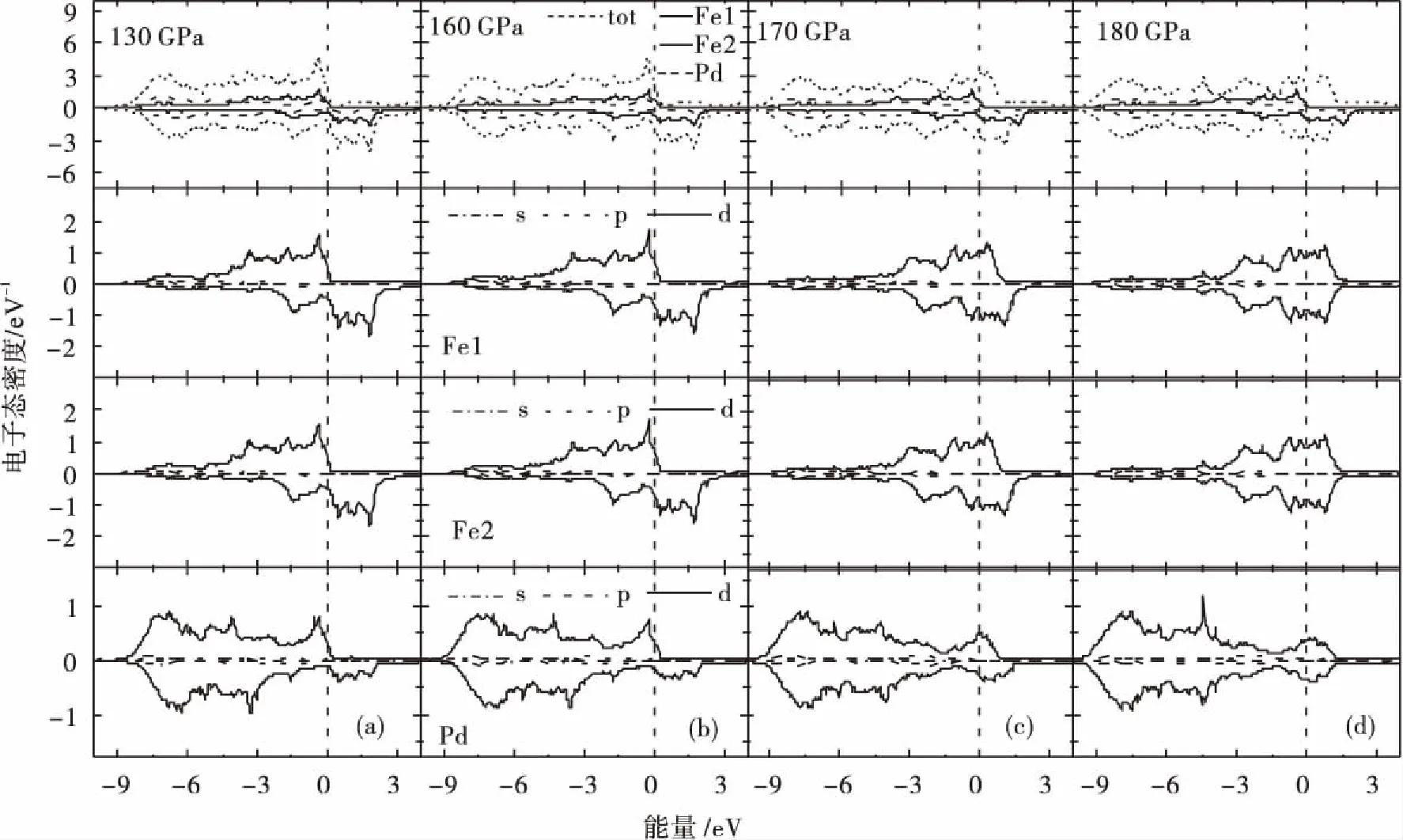
图5 130～180 GPa压力下L10-FePd的电子态密度

3 结 论

利用密度泛函理论研究了L10-FePd晶态合金在压力为0～230 GPa区间的晶体结构、焓差、磁性以及电子结构，得出如下结果：

(1) 在0～170 GPa压力区间内，考虑自旋极化的L10-FePd晶态合金比不考虑自旋极化的体系更稳定，即考虑磁性的体系更稳定，体系为铁磁态晶态合金.

(2) 随着压力的增大，铁磁态L10-FePd晶态合金的磁矩不断减小，当压力大于170 GPa时，考虑磁性的体系与不考虑磁性体系的焓基本相同，电子态密度趋于完全对称，磁矩完全消失，即铁磁性坍塌临界压力为170 GPa，从上述三方面可以看出发生了铁磁态到顺磁态的磁性相变.

我们的计算为实验工作提供了理论参考，未来我们将继续研究L10-FePd晶态合金的弹性性质、晶格动力学等物理特性.

[1] KAKESHITA T,ULLAKKO K.Giant Magnetostriction in Ferromagnetic Shape-memory Alloys[J].MRS Bulletin,2002,27(2):105-109.

[2] SHIMA H,OIKAWA K,FUJITA A,et al.Lattice Axial Ratio and Large Uniaxial Magnetocrystalline Anisotropy in L10-type FePd Single Crystals Prepared Under Compressive Stress[J].Physical Review B,2004,70(22):224408-224415.

[3] KELLY P E,O′GRADY K,MAYO P I,et al.Switching Mechanisms in Cobalt-phosphorus Thin Films[J].IEEE Transactions on Magnetics,1989,25(5):3881-3883.

[4] 李民,梅良模.Fe/Pd金属超晶格的磁性和内转换电子Mössbauer谱研究[J].物理学报,1992,41(8):1361-1367.

[5] 施一生.Fe1-xPdx合金电子结构和磁性的理论研究[J].物理学报,2003,52(4):993-998.

[6] KRESSE G,FURTHMÜLLER J.Efficient Iterative Schemes for Ab Initio Total-energy Calculations Using A Plane-wave Basis Set[J].Physical Review B Condens Matter,1996,54(16):11169-11186.

[7] KRESSE G,FURTHMÜLLER J.Efficiency of Ab-initio Total Energy Calculations for Metals and Semiconductors Using A Plane-wave Basis Set[J].Computational Materials Science,1996,6(1):15-50.

[8] KRESSE G,JOUBERT D.From Ultrasoft Pseudopotentials to the Projector Augmented-wave Method[J].Physical Review B,1999,59(3):1758-1775.

[9] PERDEW J P,BURKE K,ERNZERHOF M.Generalized Gradient Approximation Made Simple[J].Physical Review Letters,1996,77(18):3865-3868.

[10]KRESSE G,HAFNER J.Ab Initio Molecular Dynamics for Liquid Metals[J].Physical Review B Condens Matter,1993,47(1):558-561.

[11]BLÖCHL P E.Projector Augmented-wave Method[J].Physical Review B Condens Matter,1994,50(24):17953-17979.

[12]HULTGREN R,ZAPFFE C A.The Crystal Structures of the Iron-palladium Superlattices[J].Zeitschrift Für Kristallographie-crystalline Materials,1938,99(1/6):509-512.

[13]MESCHEL S V,PAVLU J,NASH P.The Thermochemical Behavior of Some Binary Shape Memory Alloys By High Temperature Direct Synthesis Calorimetry[J].Journal of Alloys and Compounds,2011,509(17):5256-5262.

[14]CHEPULSKII R V,BARABASH S V,ZUNGER A.Ab Initio Theory of Phase Stability and Structural Selectivity in Fe-Pd Alloys[J].Physical Review B,2012,85(14):144201-144223.

[15]VLASOVA N I,POPOV A G,SHCHEGOLEVA N N,et al.Discovery of Metastable Tetragonal Disordered Phase upon Phase Transitions in the Equiatomic Nanostructured FePd Alloy[J].Acta Materialia,2013,61(7):2560-2570.

[16]YUASA S,MIYAJIMA H,OTANI Y,et al.Magnetism of Body-centered Tetragonal FeRh1-xPdxAlloys (I) Magnetic Properties[J].Journal of the Physical Society of Japan,1995,64(12):4906-4913.

声 明

为适应我国信息化建设的需要，实现科技期刊编辑、出版发行工作的电子化，推进科技信息交流的网络化进程，我刊现已入编“万方数据——数字化期刊群”、《中国学术期刊(光盘版)》、《中国期刊网》、《中文科技期刊数据库》.其作者著作权使用费与本刊稿酬一次性给付.如作者不同意将文章编入上述数据库，请在来稿时声明，本刊将作适当处理.

《沈阳化工大学学报》编辑部

Study of the Properties in the L10-FePd Crystalline Alloy at High Pressure

YU Guo-liang， CHENG Tai-min， ZHANG Hui， XU Ce

(Shenyang University of Chemical Technology， Shenyang 110142， China)

The structural stability,lattice constants,enthalpy difference,magnetic properties and electronical density of states of the L10-FePd crystalline alloy at high pressure were investigated by using first-principles calculation based on the density functional theory (DFT) within the framework of generalized gradient approximation (GGA).The results of calculation show that the system of considering the magnetic is more stable than without considering magnetic at the pressure below 170 GPa.The L10-FePd crystal alloy is ferromagnetic and the magnetic moment decrease with the pressure increase.When the pressure is above 170 GPa,the enthalpy of the system considering the magnetic is same with the without system the ferromagnetism disappear,and the electronic polarizationdensity of states becomes symmetrical.As the facts the ferromagnetic collapse critical pressure of tetragonal phase L10-FePd ferromagnetism alloy is near 170 GPa.

high pressure； L10-FePd crystalline alloy； ferromagnetic collapse critical pressure； electronical density of states

2016-11-09

国家自然科学基金面上项目(11374215)

禹国梁(1992-)，男，辽宁盖州人，硕士研究生在读，主要从事磁性物理及材料物性的研究.

成泰民(1970-)，男，辽宁沈阳人，教授，博士，主要从事磁学及磁性材料物性的研究.

2095-2198(2017)01-0091-06

10.3969/j.issn.2095-2198.2017.01.016

O521+.2

A