基于格子Boltzmann方法预测多孔介质的渗透率

战洪仁， 侯新春 ， 曹 颖， 李雅侠， 张先珍

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

基于格子Boltzmann方法预测多孔介质的渗透率

战洪仁， 侯新春 ， 曹 颖， 李雅侠， 张先珍

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

多孔介质内的流动涉及许多工程应用.文章采用不可压缩的格子Boltzmann模型对多孔介质中的流场进行数值模拟，从微细尺度上得到多孔介质的结构特性及分布情况;同时，获得了多孔介质的渗透率与孔隙率近似成指数的变化关系.根据达西定律和格子Boltzmann方法进行数值模拟，成功获得多孔介质的渗透率，为有效研究孔隙尺度下的渗流问题提供了方法，同时为多孔介质的工程应用及理论研究提供了依据.

多孔介质； 格子Boltzmann方法； 孔隙率； 渗透率

目前许多工程问题都涉及到了流体在多孔介质内的流动，比如在油气藏开发、地下水污染、地质学等等[1]中都可以通过模拟来预测流体的平均、总体的流动特性.渗透率是多孔介质流体流动特性中的重要参数之一.本文从流动状态出发，利用格子Boltzmann方法(LBM)对这一问题进行分析.

近年来，LBM作为一种新颖的介观数值模拟方法已经成功地应用在许多多孔介质流的研究中.在描述连续介质时,LBM与传统的宏观方程描述有本质的不同，该方法遵循从微观层次描述内部流动，并连续取离散的新途径，它将连续介质看作大量位于网络节点上的离散流体质点粒子,粒子按碰撞和迁移规则在网格上运动，通过对各网格流体质点及运动特征的统计，获得流体宏观运动规律[2]，其最常用的数学模型为LBGK模型.本文采用LBM模拟得到多孔介质内的流动特性以及不同孔隙率下渗透率的变化特点，为成功获得多孔介质的渗透率提供了有效方法.

1 格子Boltzmann法

采用LBGK模型，其对应的方程如下[3]：

(1)

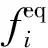
以二维正方形格子D2Q9模型(DdQq命名规则，d代表维数，q代表离散的速度方向个数)为例，其离散速度模型如图1所示.

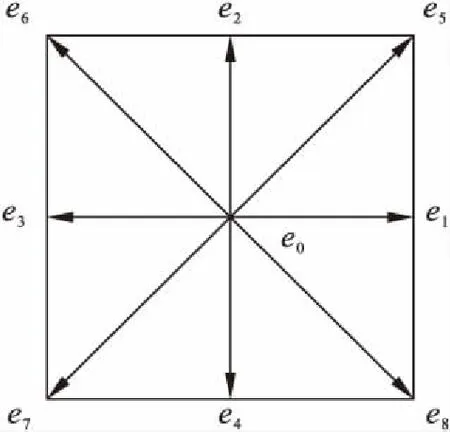
图1 D2Q9模型

粒子的离散速度：

(2)

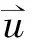
(3)

(4)

LBM的演化过程主要是由“流动”和“碰撞”组成，这两步交替循环进行，直到流速收敛为止.

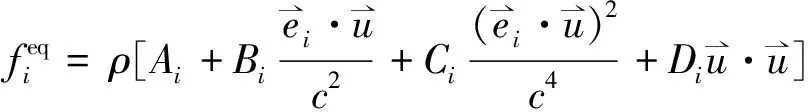
(5)

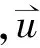
(6)

由此得到格子上粒子的局部平衡分布函数为：

(7)

式中：ωi为第i速度方向的权重系数.

将式(7)与宏观上描述流体流动的二维N-S方程进行类比可得到如下关系：

(8)

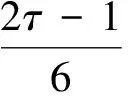
(9)

(10)

采用的参数均为无量纲.此外，边界条件的处理在格子方法中起着重要的作用，对LBM模型数值模拟的精度、稳定性以及计算效率产生很大的影响.LBM的边界处理方法简单易行，且灵活多变[7].

2 模拟结果与讨论

2.1 计算模拟

采用的多孔介质计算区域如图2所示，由Nx×Ny=303×101的格子所划分，高度H=101 mm，长度L=3H，多孔介质骨架为方柱型，边长为D，通过输入不同数值D来确定多孔介质的孔隙率.边界条件:上下边界取周期边界条件，流体与固体骨架表面采用半步长反弹格式的无滑移边界[8]，出口为自由边界.

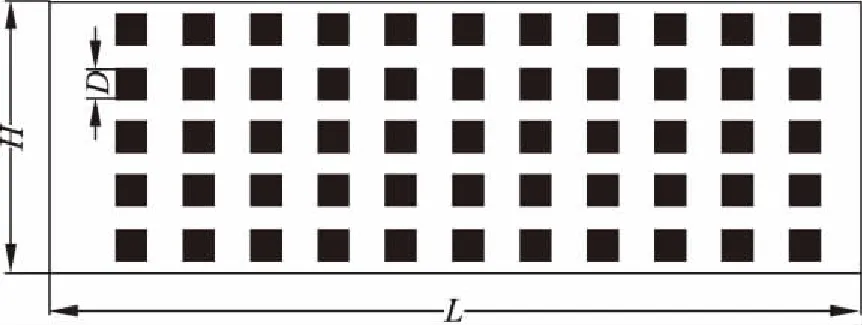
图2 方柱多孔介质区域

2.2 达西定律的应用

经典的达西定律被广泛用来描述多孔介质内流体的流动问题，并用来计算多孔介质渗透率.达西定律公式为[9]：

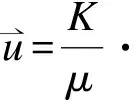
(11)

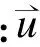
图3是方柱直径取D=10、多孔介质的孔隙率ε=82.02 %时，应用LBM模拟得到的多孔介质区域中的一部分速度场，流体是从左边界流进的，如图3所示.从图3中可以看出：X轴方向孔道中的流速明显大于Y轴方向孔道中的流速，这是因为该边界条件下，压力梯度主要存在于X方向.从图3中可以获得多孔介质本身的特性，如介质的拓扑结构、孔隙和裂缝的分布情况，且可根据模拟结果，获得如图4所示的不同雷诺数和压差的关系.从图4中可以看出：模拟结果和Ergun、Burke and Plummer、Marcom等人公式所得出的数据趋势基本符合.其中，当Re/(1-ε)在小于10时，近似呈线性关系，而当Re/(1-ε)大于10时，随着Re的增大，压降越来越小，减小趋势变缓.

图3 多孔介质内的速度矢量场

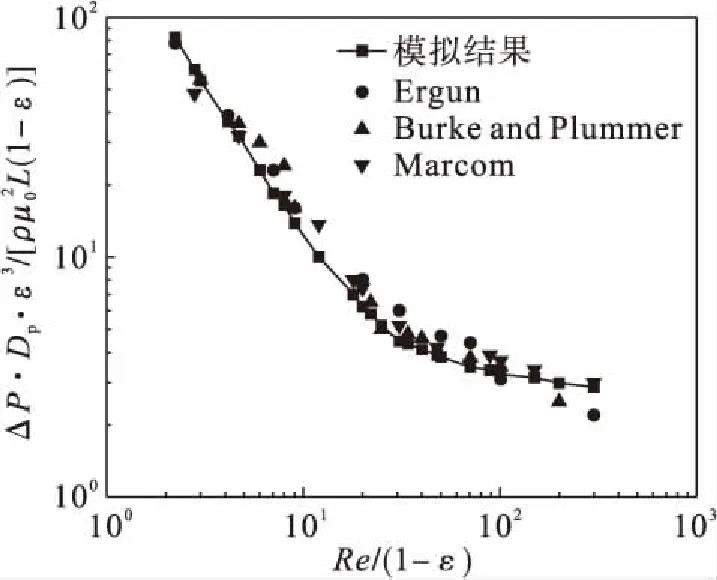
图4 压力梯度与雷诺数的关系

2.3 渗透率的确定

由上述模拟可以得到多孔介质的渗透率.渗透率表征多孔介质对流体的渗透能力，是多孔介质的一个重要特性参数，是渗流力学计算中最重要的输入参数之一，通过试验方法很难准确得到多孔介质的渗透率.

对于简单几何构造的结构，可以用LBM数值模拟计算其渗透率.许多研究者都曾使用二维周期性结构进行数值试验，其中包括Eidsath Coulaud Sahraoui、Kaviany Flower、Bejan以及Nakayama等.1995年，Nakayama等人对立方体晶格中的重复发展流体进行了三维数值计算，并证明了Carman-kozeny提出的水力半径理论完全能够胜任立方体的渗透率估算[10]，立方体的渗透率估算如下：

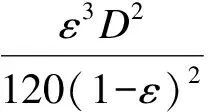
(12)

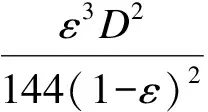
(13)

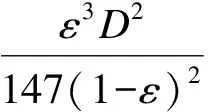
(14)

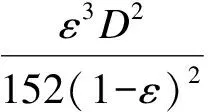
(15)

以上公式都接近于Carman-kozeny的经验表达式：

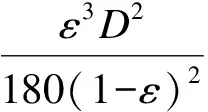
(16)

在上述方程中K为渗透率，ε为孔隙率，D即表示方块和立方体的大小，同时也表示横流中球体和圆柱体的直径.

图5为由模拟结果根据式(16)绘制得到的孔隙率与渗透率的关系图，并与已发表的结果作了对比.图5可以反映出本文的数值结果，其孔隙率与渗透率近似成指数关系变化:K=AεB，与前人研究的结果相吻合.

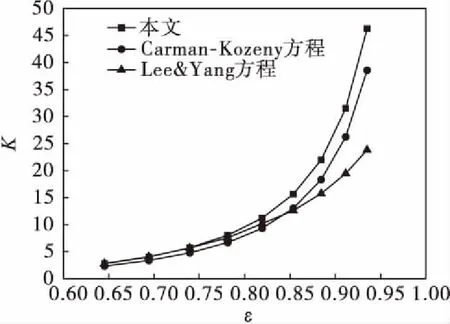
图5 渗透率与孔隙率之间的关系

用最小二乘法拟合数值模拟结果，得A=89.873 1，B=10.652 8，所以变化公式为K=89.873 1ε10.652 8.从图5中可以看出：当孔隙率大于0.78时，本文结果与Lee和Yang[11]所提出的公式发生偏离，随着孔隙率的增大，偏离越来越大.这可能是由两个原因造成的：一方面文献中所采用的多孔介质模型是圆柱，本文采用的是方柱；另一方面，本文的排列为规则排列，而文献中是交错排列的.由上述结论可知，应用LBM，通过上述计算得到的压降可以简单地获得多孔介质的渗透率.

3 结 论

应用格子Boltzmann方法的LBGK模型成功模拟了多孔介质中流动特性，并进行了数值模拟，多孔介质内流体的流动状态受到模型的影响.通过对此问题的详细研究，得到如下结论：

(1) 通过计算得到多孔介质内压降与雷诺数的关系，当Re/(1-ε)小于10时，压降随雷诺数的增大而减小，近似呈线性关系；当Re/(1-ε)大于10时，减小趋势减缓.

(2) 经过数值模拟结果和相关分析：在本文的研究条件下，渗透率与孔隙率近似成指数关系变化，K=89.873 1ε10.652 8；根据LBM数值模拟和达西定律可以成功预测多孔介质的渗透率，并与经验公式值作对比，趋势基本符合.

(3) 通过模拟获得了一些多孔介质本身特性，如介质的拓扑结构、孔隙和裂缝的分布情况.

[1] SCHEIDEGGER A E.The Physics of Flow Through Porous Media[J].Soil Science,1958,86(6):355.

[2] 袁竹林,蔡桂英.圆柱绕流现象的格子玻耳兹曼数值模拟[J].中国电机工程学报,2004,24(8):162-165.

[3] CHEN S,DOOLEN G D.Lattice Boltzmann Method for Fluid Flows[J].Annual Reviews of Fluid Mechanics,1998,30(1):329-364.

[4] GUO Z L,SHI B C,ZHENG C G.A Couple Lattice BGK Model for the Boussinesq Equations[J].Internation Journal for Numerical Methods in Fluids,2002,39(4):325-342.

[5] 刘慕仁,陈若航,李华兵，等.二维对流扩散方程的格子Boltzmann方法[J].物理学报,1999,48(10):1800-1803.

[6] CHEN H D,CHEN S Y,MATTHAEUS W H.Recovery of the Navier-stokes Equations Using a Lattice-gas Boltzmann Method [J].Physical Revew A,1992,45(8):R5339-R5342.

[7] 何雅玲,王勇,李庆.格子Boltzmann方法的理论及应用[M].北京:科学出版社，2009:7-8.

[8] ZIEGLER D P.Boundary Conditions for Lattice Boltzmann Simulations[J].Journal of Statistical Physics,1993,71(5):1171-1177.

[9] 孔祥言.高等渗流力学[M].合肥:中国科学技术大学出版社,1999:31-39.

[10]刘仁兴.不同粒径分布多孔介质渗流的微观数值模拟研究[D].武汉:武汉工业学院,2012:6-8.

[11]LEE S L,YANG J H.Modeling of Darcy-forchheimer Drag for Fluid Flow Across a Bank of Circular Cylinders[J].International Journal of Heat and Mass Transfer,1997,40(13):3149-3155.

Prediction of Permeability in Porous Media Based on Lattice Boltzmann Method

ZHAN Hong-ren, HOU Xin-chun, CAO Ying, LI Ya-xia, ZHANG Xian-zhen

(Shenyang University of Chemical Technology, Shenyang 10142, China)

The fluid flow in porous media is involved in various engineering applications,e.g.permeability has significant research value in oil and gas exploration field.In this paper,the flow field in porous media is simulated using incompressible lattice Boltzmann model,by which structure characteristics and distributions of porous medium were obtained with micro scale.Meanwhile,the permeability of porous media varied exponentially with the porosity of porous media.The permeability of porous medium can be successfully and directly predicted basing on numerical simulation of lattice Boltzmann method and Darcy law.The simulation provide an effective method to study the interstitial flow in micro scale,and also a foundation for the theoretical research and engineering application of porous media.

porous media; lattice Boltzmann method; porosity; permeability

2014-12-08

辽宁省博士科研启动基金项目(20141085)

战洪仁(1964-)，女，山东蓬莱人，副教授，博士，主要从事强化传热与节能技术的研究与应用.

2095-2198(2017)01-0063-04

10.3969/j.issn.2095-2198.2017.01.011

O357.3

A