基于材料强度既有统计参数的梁桥地震易损性简化分析方法

张 云， 谭 平， 黄佳栋，， 黎力韬

(1.广西交通科学研究院有限公司，南宁 530007；2.广州大学 土木工程学院，广州 510405；3.广西翔路建设有限责任公司, 南宁 530029)

基于材料强度既有统计参数的梁桥地震易损性简化分析方法

张 云1，3， 谭 平2， 黄佳栋1，2， 黎力韬1

(1.广西交通科学研究院有限公司，南宁 530007；2.广州大学 土木工程学院，广州 510405；3.广西翔路建设有限责任公司, 南宁 530029)

为了研究简化的地震易损性方法在桥梁中的应用，通过寻求材料不确定性的统计规律，达到简化易损性分析的目的，提出了两种易损性简化分析方法。针对我国实际工程中应用最为广泛的某梁式桥梁，采用拉丁超立方抽样来进行结构材料不确定性组合，对桥梁的三维有限元模型，选用了10条天然地震动，利用结构主要材料既有的统计规律，对比研究了两种易损性简化分析与常规基于位移的地震易损性分析方法的计算结果。研究结果表明：采用简化分析方法一得到的桥梁结构地震需求超过其性能水平的超越概率要小于常规基于位移的地震易损性分析方法的计算结果，其结果偏于不安全，而且有一定的误差；采用简化方法二绘制的易损性曲线比简化方法一绘制的易损性曲线更接近常规方法的，其误差更小，其分析结果偏于安全；采用简化分析方法之二，将大幅减少分析样本数量，在实际工程中可以用来对桥梁结构地震破坏状态概率进行近似估计。

材料强度；统计参数；易损性简化分析；拉丁超立方；位移

displacement

美国太平洋地震工程研究中心(PEER)于20051年提出了新一代基于性能的地震工程研究框架，其中地震易损性分析为该框架重要环节和热点之一[1]。

桥梁的抗震性能取决于自身的几何性质、材料性质、地震动强度及场地条件等不确定性因素。结构遭受地震作用后，通常需定义桥梁的不同损坏状态，从而以易损性曲线的形式评估桥梁的抗震性能，并在建立易损性曲线的基础上，预估桥梁系统震后损失和修复成本[2]。对于建立理论易损性曲线量化结构损坏状态的研究，前人主要基于理论计算或试验分析来定义桥梁构件的损坏水准。Alam等[3]对比了分析了不同的损伤状态中的桥梁系统与部件的易损性曲线。郑山锁等[4]基于材料性能退化模型进行了单层单跨钢排架结构的地震易损性分析，并得到了钢排架结构抗震性能随龄期变化的一般性规律。Dutta等[5]针对抗震和非抗震设计的桥墩柱，通过试验分别进行荷载循环测试，制定了不同损伤水准下的转动漂移阈值。Ramanathan等[6]对加利福尼亚混凝土箱梁桥的地震易损性曲线的时间演化进行了研究。Ghosh等[7]考虑桥梁性能随时间变化时，基于改进的退化模型对高速路旧梁的易损性进行了评价，并指出时间依存的预测函数可以为桥梁抗震可靠性评价提供合理精度的逻辑回归系数。

从地震易损性分析的原理上看，易损性分析实质上是结构损伤概率分析，为得到分析结果，必须对大量的结构样本分析后得到统计参数，从而绘制易损性曲线。但是，大样本计算分析的工作量非常大，对单一桥梁的计算尚可接受，但对于分布于公路网上大量的中、小跨径桥梁进行全面的易损性分析来指导公路网地震应急预案的制定，其工作量将大到难以接受的地步。本文针对基于位移的地震易损性曲线，提出了两种易损性的简化分析方法，并将这两种简化方法与常规方法进行了对比分析，期待在桥梁地震易损性分析的简化方法上做一些探索。

1 基于位移易损性曲线

1.1 基于位移的地震易损性分析方法

桥梁结构的地震易损性是指在不同地震强度作用下，桥梁结构发生各种破坏状态的概率，通常用地震易损性曲线来描述。基于计算分析的地震易损性分析方法主要有基于倒塌机制分析法，基于能力谱分析法与基于位移分析法。基于倒塌机制分析的地震易损性分析方法仅能考虑倒塌极限状态这一种极限状态。基于能力谱分析的地震易损性分析方法根据美国的数据库得到的，这使得其他地区在运用该方法时要重新计算，且该方法用Pushover曲线来表示结构的非线性特性需要了解大量的结构信息(如配筋等)，这对于大范围进行的易损性分析方法来说无疑要消耗大量的人力、财力和工时。基于位移的地震易损性分析采用位移作为破坏的判别因子以及地震需求的代表值，这种方法满足易损性分析方法要求：地震需求和结构破坏相关、易于界定破坏状态、概念明确、计算简单以及可考虑结构参数的概率分布。对于地震动强度的描述，谱加速度Sa的离散性普遍认为小于PGA的离散性[8]。可以用下式来求解结构超越既定位移限值Xi的超越概率Pf。

(2)

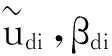
采用基于位移的地震易损性分析方法进行震害预测时，若按照上述式(1)全概率分析方法，对单座桥梁都需要同时考虑地震动的随机性和结构自身的不确定性，通过弹塑性结构动力反应来计算结构反应，其计算工作量非常大，需要耗费相当多的计算工时，而且后期的数据归纳和统计工作量也是巨大的。在实际应用时，对于一个区域(如若干个城市和大片农村)的桥梁往往有多座，难以对每座桥梁进行精确计算，只能粗略预测，而且在国内经济快速发展形势下，各种新型复杂桥梁层出不穷，无法做长时间的细致的研究，因而，寻找更简单易行适合的易损性评估计算方法是十分必要的。

由于影响桥梁地震震害的因素分为两大类，一类是地震动的不确定性，一类是结构本身的不确定性。结构本身的不确定因素很多，各个因素所占的权重差异比较大。在震害预测时，难以考虑所有因素的影响，只能考虑对桥梁损伤起主要作用的因素。桥梁本身的不确定性主要与建筑材料的不确定性有关，也就是与混凝土和钢筋的变异性有关。

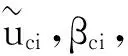
地震动的不确定性是结构易损性分析的基础，没有地震动的不确定性，结构地震易损性分析也就失去了意义，而且地震动是自然界最复杂的自然现象之一，没有统计规律可循[11]。因此，本文把易损性分析的简化集中在参数n，即寻求材料不确定性的统计规律，减小参数n的数值，从而减小分析样本的数量，达到简化分析的目的。基于上述思路，本文提出两种简化分析方法。

1.2 简化分析方法之一

相对于地震动的随机性来说，材料强度的随机性是可控的，是有规律的分布在一定的范围之内，《混凝土结构设计规范》当中材料强度的标准值就是具有95%保证率的材料强度的平均值。在进行结构地震易损性分析过程中，如果以规范规定的材料强度标准值作为时程分析模型中材料的性能指标，不考虑材料强度的随机性，就可以大幅度的减少结构计算的工作量和后期数据归纳和统计的工作量，极大的提高结构易损性分析的效能。

(3)

结构样本数量从n × l × m个减少为l × m个，结构分析工作量承数量级减少。这种简化方法的实质是采用根据规范中材料强度的标准值，不考虑桥梁同类材料强度的差异，给出的是一种基于半概率的易损性曲线。这种方法虽然在一定程度上不能准确描述地震需求的变异性，但是总体上可以满足结构地震易损性分析的要求，且减小的计算工作量，简化了分析步骤，便于桥梁易损性计算大范围的推广应用。

1.3 简化分析方法之二

简化分析方法一利用材料强度的平均值进行结构地震易损性分析，虽然可以大幅度的减少结构计算的工作量，但是没有考虑材料固有的随机性问题，必然带来一系列的误差。

我国的科研人员从20世纪80年代开始持续的对国内主要的几种钢筋型号的强度变异系数和大部分混凝土标号的强度变异系数进行统计，并将其统计结果应用于自1989年开始的《混凝土结构设计规范》中。2008—2010年研究人员再次对全国的钢筋强度与商品混凝土参数进行了统计分析，结果表明，与20世纪80年代的统计结果相比，目前的材料强度变异系数略有减小。考虑材料的变异系数δs作为结构性能的变异系数，按照统计学原理，服从对数正态分布的函数其对数均值βci ln与变异系数的关系式如下所示：

(4)

表1 计算效率的对比

2 算 例

2.1 桥梁描述及数值模拟

分析模型选用了我国公路网中最常用的30 m先简支后连续预应力混凝土T型梁桥作为代表性桥梁结构，桥梁宽度12 m。桥梁主梁由6片T型梁组成，单梁宽与高为2 m× 2 m，单梁质量85 t。墩柱为圆形柱式，由上至下依次为1.5 m和1.8 m两种直径，1号、6号墩柱高14 m，2号、3号墩柱高22 m，4号、5号墩柱高18 m。桥墩墩柱采用C30混凝土，1.5 m墩柱配置38根25 mm HRB335钢筋，配筋率为1.06%，1.8 m墩柱配置38根28 mm HRB335钢筋，配筋率为0.92%；箍筋采用10 mm HPB235钢筋，螺旋配置，间距为200 mm，在墩柱顶、底塑性铰区域加密为100 mm间距。

上部结构在地震作用下基本保持弹性，因而采用线弹性梁柱单元模拟，桥台处滑板支座采用滞回系统模拟，桥墩处普通板式橡胶支座及抗震销采用弹性连接单元及间隙单元综合模拟[12]，墩柱由于要承受巨大的地震力，允许桥墩在强震作用下形成塑性铰，故墩柱采用弹塑性纤维梁柱单元来模拟。为简化起见，本例中不考虑桩土共同作用，假定墩底固结，结构有限元计算模型,如图1所示。

图1 典型梁桥结构有限元分析模型Fig.1 Finite element model of typical beam bridge structure

2.2 地震动输入的不确定性

算例在美国太平洋地震研究中心(PEER)数据库中选择10条震级为6～8级实际地震动记录作为地震动输入，其断层距离为9.06～36.30 km，峰值加速度为0.084～0.417 m/s2。以谱加速度Sa作为调整基准，为方便计算，按照设计谱的特征周期和天然地震动均值谱的最大值，在特征周期0.4 s处将天然地震动的谱加速度按调整为1.0g，然后以0.15g为间隔值，按比例将天然地震动按比例调整为0.15g～1.50g，形成10组共100条不同强度的地震动，即l×m=10× 10。图2为所选择的天然震波反应谱和均值反应谱。

图2 天然地震动反应谱谱值图Fig.2 Spectrum value of natural ground motions

2.3 材料的不确定性

桥梁结构材料主要为混凝土与钢筋两种，而为标准化施工绝大多数构件的混凝土标号与钢筋等级基本一致。根据《混凝土结构设计规范》(GB 50010—2010)对2008—2010年统计结果，钢筋与混凝土均符合正态分布规律，其中C30混凝土强度变异系数为17.2%，HPB235及HRB335钢筋强度变异系数分别为8.95%及7.43%。

根据拉丁超立方抽样原理，将C30混凝土分布函数等分为16份，每一份对应于其概率密度函数，将其分为16块，每一块面积重心所对应的混凝土强度值则为样本取值。对于R235钢筋和HRB335钢筋，其强度也服从正态分布，样本取值方法与C30混凝土相同。材料强度样本如表2所示。再采用随机抽样方法，对16组样本进行随机排列，作为桥梁结构易损性分析中的材料不确定性分析的基础。

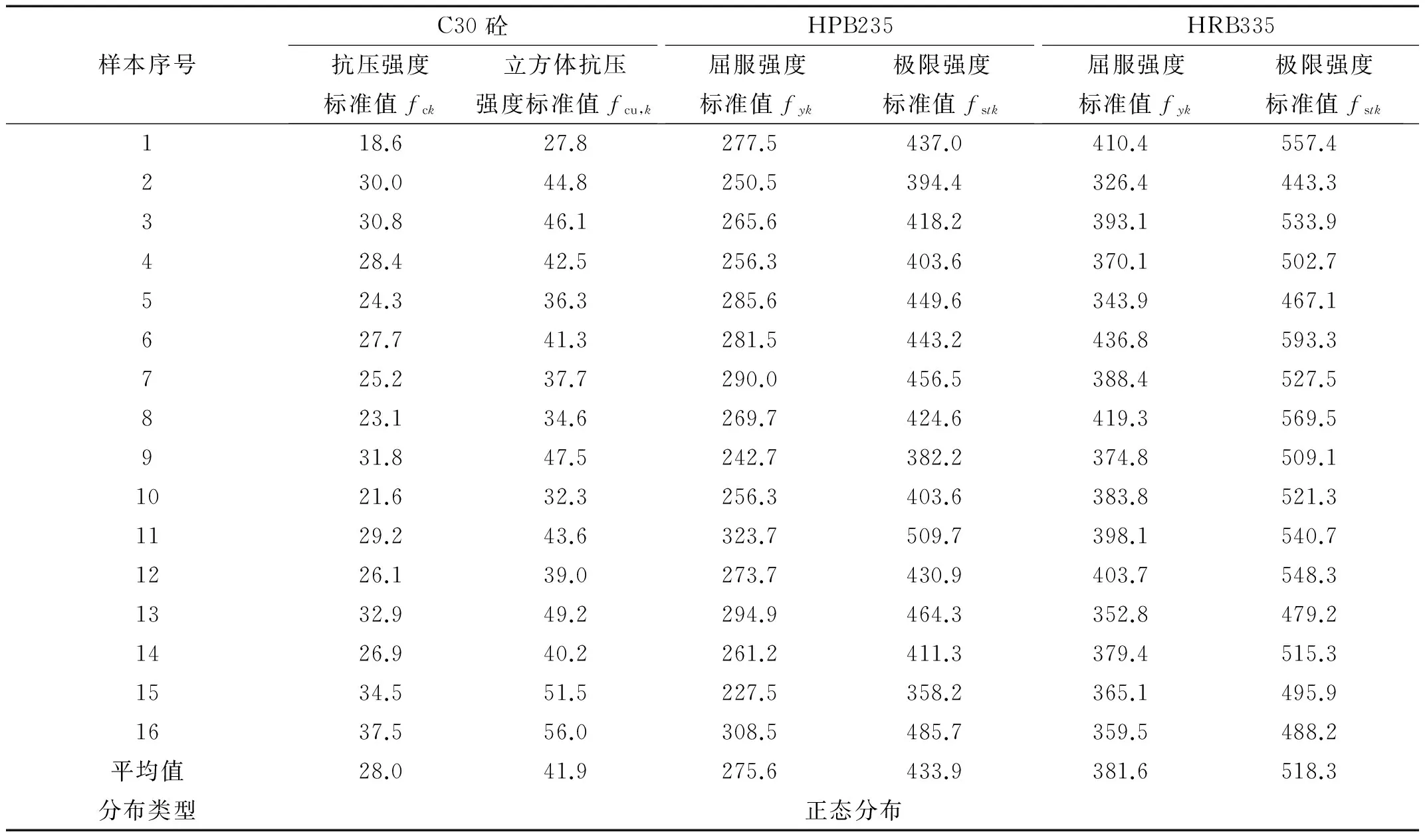
表2 主要材料强度样本表

2.4 桥梁位移限值统计分析

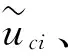
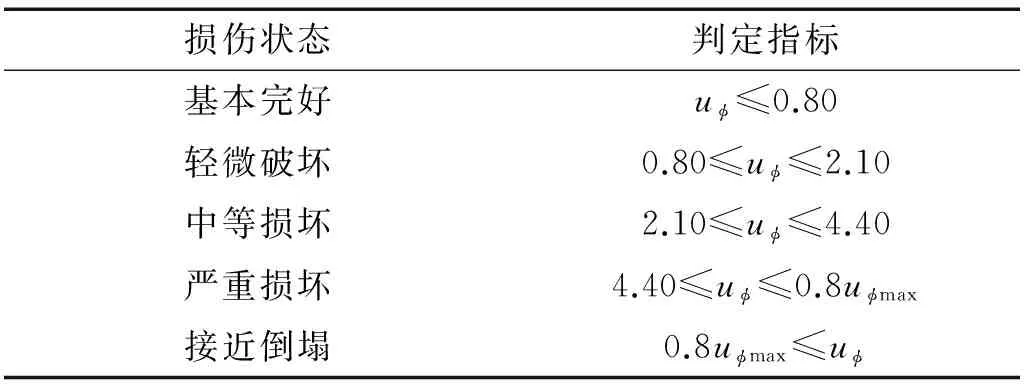
表3 曲率延性比定义的墩柱破坏状态表

2.5 桥梁位移反应统计分析

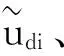
按反应谱0.3g、0.6g、0.9g、1.2g分别对应于规范规定的7度(0.1g)、8度(0.2g)、8度(0.3g)、9度(0.4g)设计谱，将桥梁结构反应与设计地震动强度联合分析，绘制得到桥梁的地震易损性曲线，如图3所示。

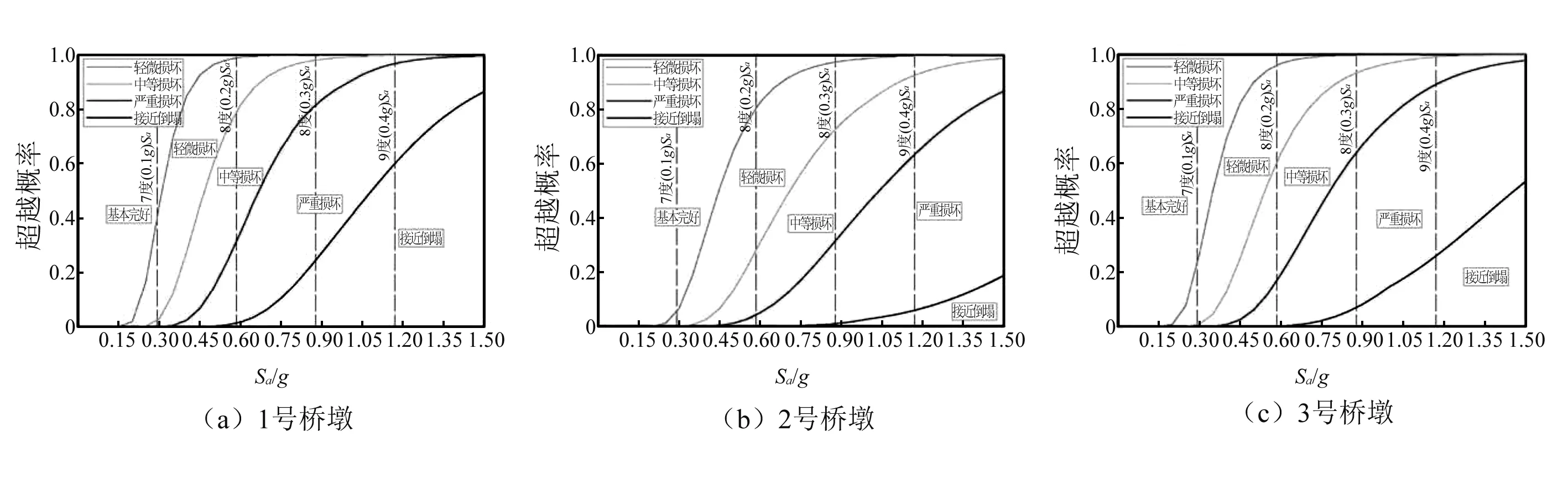
图3 基于设防水准的桥梁地震易损性曲线Fig.3 Pier seismic fragility curves based on seismic fortification level

表4 1号桥墩样本位移限值统计表

Tab.4 Statistics of limit displacement of sample No. 1 pier m

2.6 三种方法桥梁易损性分析对比

图4中，灰色虚线为采用简化分析方法之一绘制的易损性曲线，浅灰色实线为采用全概率方法绘制的易损性曲线。采用简化分析方法之一绘制的易损性曲线与基于全概率方法计算得到的易损性曲线，总体上比较接近，因此可以说明简化方法的合理性。简化分析方法之一曲线全部居于全概率曲线下方，说明采用简化分析方法之一算法得到的桥梁结构地震需求超过其性能水平的超越概率要小于全概率方法的计算结果，其结果偏于不安全，而且有一定的误差，产生误差的主要原因是简化分析方法之一没有考虑桥梁材料的不确定性。

图4中，黑色实线为采用简化分析方法之二绘制的易损性曲线，从图4可知，采用简化分析方法之二绘制的易损性曲线相对于简化分析方法之一绘制的曲线更接近全概率方法绘制的曲线，其误差更小，为保证整个曲线处于全概率曲线的上方，计算出偏于安全的结果，在不同材料变异系数的取值时，一般选取最小值作为最终计算参数。

表5 桥墩位移限值统计表

Tab.5 Statistics of pier limit displacement

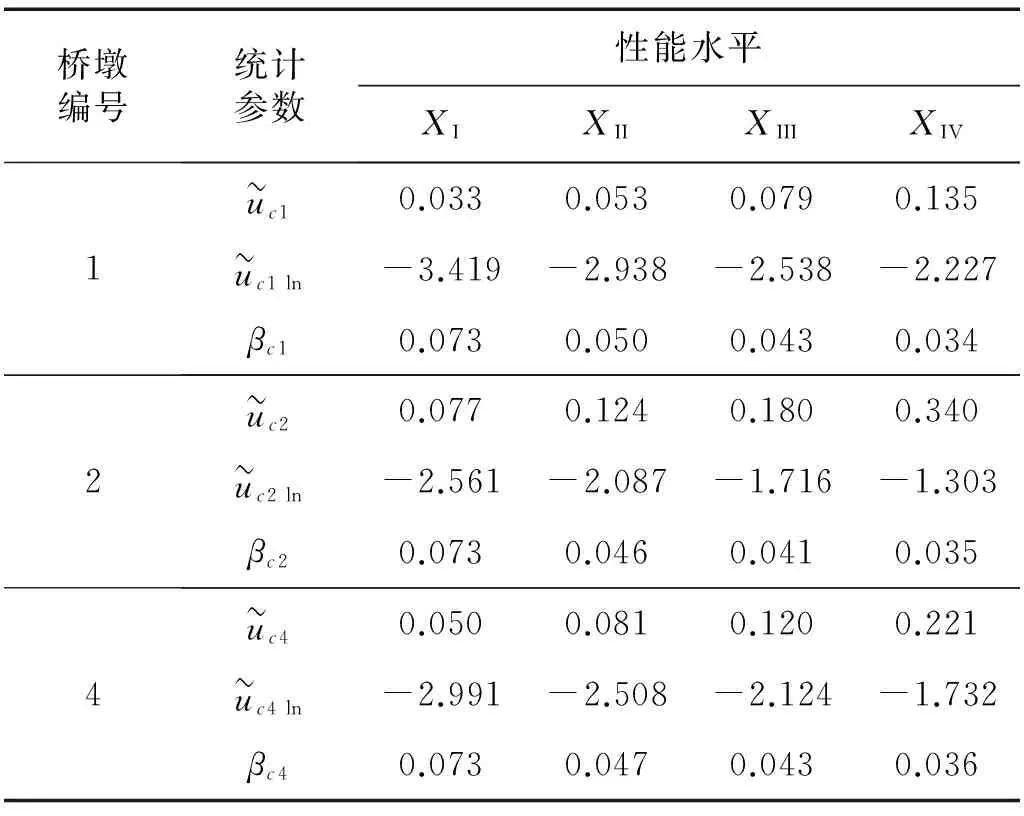
m

表6 桥墩位移反应统计表

Tab.6 Statistics of pier reaction displacement m

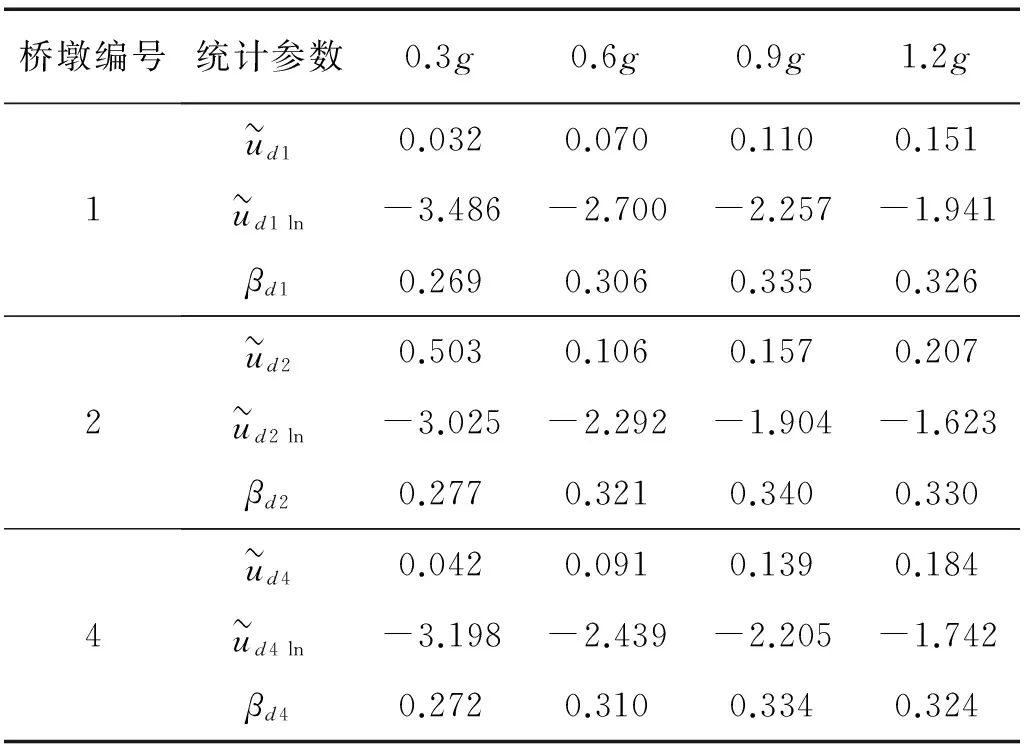
图4 三种方法绘制的4号桥墩地震易损性曲线Fig.4 Seismic fragility curves of No. 4 Pier

3 结 论

本文利用桥梁结构主要材料既有的统计参数，在基于全概率易损性分析方法的基础上，提出了两种简化分析方法，并对这两种简化方法绘制的易损性曲线进行了误差分析。

第一种简化方法的实质是采用根据规范中材料强度的标准值，不考虑桥梁同类材料强度的差异，给出的是一种基于半概率的易损性曲线。第二种简化方法的实质是根据规范里面给出的材料变异系数来考虑了钢筋与混凝土材料的强度偏差，而求得的一种易损性曲线。

第一种简化方法绘制的易损性曲线处于基于全概率方法绘制的易损性曲线的下方，结果偏于不安全，而且地震动越大，结果偏差越大。简化方法之二位于全概率方法绘制的易损性曲线的上方，结果偏于安全，相对于简化方法之一绘制的易损性曲线更接近基于全概率方法绘制的，其误差更小。

在对大批量普通中、小跨径梁式桥进行地震易损性分析时，可以利用结构材料自身的统计参数，对易损性分析方法进行简化，采用本文的简化分析方法之二，将大幅减少分析样本数量，得到结构地震易损性分析曲线，其结果偏于安全且误差较小，在实际工程中可以用来对桥梁结构地震破坏状态概率进行近似估计。

[1] 钟剑, 庞于涛, 曹飒飒, 等. 基于构件的RC连续梁桥地震体系易损性分析[J]. 同济大学学报(自然科学版), 2015, 43(2): 193-198. ZHONG Jian, PANG Yutao, CAO Sasa, et al. Seismic fragility methodology for RC continuous bridges based on components correlation[J]. Journal of Tongji University (Natural Science),2015, 43(2): 193-198.

[2] 吴子燕,贾兆平,刘骁骁. 基于桥梁经验数据的理论易损性曲线校准[J]. 应用数学和力学, 2014, 35(7): 723-736. WU Ziyan, JIA Zhaoping, LIU Xiaoxiao. Calibration of analytical fragility curves based on empirical data of bridges.applied[J]. Mathematics and Mechanics,2014, 35(7): 723-736.

[3] ALAM M S, BHUIYAN M A R, BILLAH A H M M. Seismic fragility assessment of SMA-bar restrained multi-span continuous highway bridge isolated by different laminated rubber bearings in medium to strong seismic risk zones[J]. Bulletin of Earthquake Engineering, 2012, 10(6): 1885-1909.

[4] 郑山锁,代旷宇,韩超伟, 等 基于材料性能退化模型的钢排架结构易损性分析[J]. 振动与冲击,2015,34(17):18-24. ZHENG Shansuo, DAI kuangyu, HAN Chaowei, et al. Steel bent frame structure vulnerability ananlysis based on steel performance degration model[J]. Journal of Vibration and Shock, 2015,34(17):18-24.

[5] DUTTA A, MANDER J B. Seismic fragility analysis of highway bridges[C]∥ Proceedings of the INCEDEMCEER Center-to-Center Workshop on Earthquake Engineering Frontiers in Transportation Systems, 1998．

[6] RAMANATHAN K, PADGETT J E, DESROCHES R. Temporal evolution of seismic fragility curves for concrete box-girder bridges in California[J]. Engineering Structures, 2015, 97(15): 29-46.

[7] GHOSH J, SOOD P. Consideration of time-evolving capacity distributions and improved degradation models for seismic fragility assessment of aging highway bridges[J]. Reliability Engineering & System Safety, 2016,154(10): 197-218.

[8] 张菊辉. 基于数值模拟的规则梁桥墩柱的地震易损性分析[D].上海：同济大学,2006.

[9] 张令心，江近仁. Latin超立方采样技术及其在结构可靠性分析中的应用[J]. 世界地震工程, 1997, 13(4):1-6. ZHANG Lingxin, JIANG Jinren. Latin hypercube sampling and its application to structural reliability analysis[J]. World Information on Earthquake Engineering, 1997, 13(4):1-6.

[10] WYSS G D, JORGENSEN K H. A user’s guide to LHS: sandia’s Latin hypercube sampling software[R]. Albuquerque, NM: SAND98-0210, Sandia National Laboratories, 1998.

[12] 张云, 谭平, 郑建勋, 等. 基于性能的中小跨径装配式梁桥地震易损性分析[J]. 振动工程学报, 2014, 27(5): 676-684. ZHANG Yun, TAN Ping, ZHENG Jianxun, et al. Fragility analysis for performance-based seismic design of prefabricated bridge with middle-small span [J]. Journal of Vibration Engineering, 2014, 27(5): 676-684.

[13] 张云, 谭平, 郑建勋, 等. 柱式柔性墩隔震梁桥结构地震易损性分析[J]. 振动与冲击, 2015, 34(16): 48-54. ZHANG Yun, TAN Ping, ZHENG Jianxun, et al. Seismic fragility analysis on isolated bridges with flexible column piers[J]. Journal of Vibration and Shock, 2015, 34(16): 48-54

[14] WANG H H，刘晶波. 地震作用下钢筋混凝土桥梁结构易损性分析[J]. 土木工程学报，2004, 37(6):47-51. WANG H H，LIU Jingbo. Seismic fragility analysis of reinforced concrete bridges[J]. China Civil Engineering Journal, 2004, 37(6):47-51.

Simplified seismic vulnerability analysis method for beam bridges based on the existing statistical parameters of material strength

ZHANG Yun1，3, TAN Ping2, HUANG Jiadong1,2, LI Litao1

(1.Guangxi Transportation Research & Consulting, Co.,Ltd., Nanning 530007, China; 2.School of Civil Engineering， Guangzhou University, Guangzhou 510405, China; 3.Guangxi Construction Co., Ltd., Nanning 530029, China)

For the purpose of analysing the seismic vulnerability of bridges, through seeking the statistical property of material uncertainty to simplify the analysis, two kinds of simplified seismic vulnerability analysis methods were proposed. Aiming at a certain kind of beam bridges, which is the most widely used in practical projects in China, the Latin hypercube sampling was adopted for the uncertainty composite of bridge structure materials. Ten natural ground motions were chosen to analyse a three dimensional finite element model of the bridge. The results of the two kinds of simplified seismic vulnerability analysis methods and the conventional method were compared by using the existing statistical regularity of the structure main material. The results show that the exceeding probability of the bridge seismic structure demands over the bridge performance level calculated by the first simplified seismic vulnerability analysis method, is less than that by the traditional method，which may tend to be unsafe compared to the traditional method. The seismic fragility curves calculated by the second simplified method are closer to those by the traditional method, which means to be much safer compared with the first simplified method. The number of analysis samples will be reduced significantly when the second simplified method is taken , which could be used to estimate the seismic damage state probability of bridge structures.

material strength；statistical parameters；simplified vulnerability analysis；Latin hypercube sampling；

973计划(2011CB013606)；广西科技攻关项目(桂科攻13550008-2)

2016-07-22 修改稿收到日期：2016-11-04

张云 男，博士，教授级高工，1977年生

谭平 男，博士，研究员，1973年生

U448.21

A

10.13465/j.cnki.jvs.2017.14.036