橡胶弹性元件低温刚度预测

丁智平， 穆龙海， 卜继玲， 黄友剑， 曾家兴

(1. 湖南工业大学 机械工程学院，湖南 株洲 412007； 2. 株洲时代新材料科技股份有限公司，湖南 株洲 412007)

橡胶弹性元件低温刚度预测

丁智平1， 穆龙海1， 卜继玲2， 黄友剑2， 曾家兴1

(1. 湖南工业大学 机械工程学院，湖南 株洲 412007； 2. 株洲时代新材料科技股份有限公司，湖南 株洲 412007)

进行温度为20 ℃, 0 ℃, -10 ℃, -20 ℃, -30 ℃，-40 ℃的橡胶试样单轴拉伸试验，研究不同应变水平下橡胶材料本构曲线的割线模量随温度变化的规律。定义橡胶试样在低温下本构曲线的割线模量与常温下的割线模量之比为橡胶材料的温度因子，将其表示为多项式函数的形式，并利用橡胶试样拉伸实验数据拟合得到不同应变水平下的温度因子。对锥形橡胶弹簧进行常温下的刚度仿真，通过温度因子对锥形簧常温下的刚度进行修正，预测其在低温下的刚度，并进行锥形簧产品在常温和低温下的刚度台架试验，结果表明环境温度高于-20 ℃时，预测刚度误差小于8%，满足工程使用要求，但是当环境温度低于-30 ℃时预测刚度误差较大。

橡胶弹性元件；单轴拉伸；低温刚度；温度因子；预测

橡胶弹性元件广泛应用于轨道交通领域，其工作的环境温度变化较大，在冬季橡胶弹性元件的工作温度可低至-40 ℃。为保证橡胶弹性元件的工作可靠性，必须保证橡胶弹性元件在低温环境下的刚度满足设计要求。由于试验条件限制，工程上很少对橡胶产品进行低温静刚度试验，因此提出一种可靠的低温刚度预测方法显得颇为重要。

在常温下橡胶材料的静态力学性能研究已经趋于成熟[1-4]，然而少有学者进行低温环境下橡胶材料的静态力学性能研究。橡胶材料的静态力学性能通常用超弹本构模型表示，为获得较为精确的材料参数，许多学者进行了大量的研究。袁东野等[5]进行了不同温度下的剪切实验，深入研究了温度的降低对橡胶材料压缩弹性模量、剪切弹性模量的影响；余惠琴等[6]等比较了天然橡胶与低温改性橡胶剪切性能;王付胜等[7]进行橡胶材料的低温试验，测试玻璃化温度并分析影响橡胶胶料低温性能的配方因素；由世岐等[8]对叠层橡胶支座进行低温垂向和横向的静刚度实验，研究环境温度对横向和垂向刚度的影响；王涛[9]进行常温和196 ℃下的基础力学实验，拟合两种工况下的超弹本构关系,并对两种环境温度下的橡胶金属复合密封机构进行了有限元分析。

环境温度改变对橡胶材料的力学特性影响较大。本文将对橡胶材料进行低温下的单轴拉伸实验，研究低温环境变化对其力学性能的影响，并提出橡胶弹性元件低温刚度预测的方法，为工程设计提供技术支撑。

1 橡胶材料的低温温度效应

橡胶类材料具有材料非线性和几何非线性的特点，属于非线性弹性材料，弹性模量随应变水平的不同而不同。为了描述橡胶材料在某一应变水平下的力学性能，本文定义材料本构曲线上对应点的割线斜率，即应力与应变之比为材料在此应变水平下的割线模量，如图1所示。

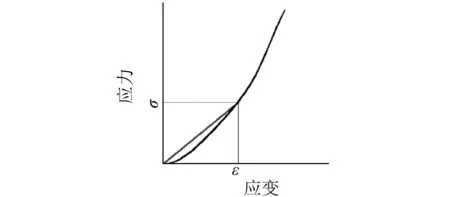
图1 橡胶材料割线模量Fig. 1 Rubber secant modulus

割线模量表达式为

(1)

式中：E为割线模量；σ为某应变水平ε下的应力。

1.1 橡胶材料的分子热运动

环境温度对橡胶材料的力学性能影响，如图2所示。对于单轴拉伸式样而言在同等载荷水平下，随温度升高橡胶材料的割线模量不断减小，橡胶分子的流动性增加，在微观上呈现出不同的分子运动形式，在宏观上表现为玻璃态、橡胶态和黏流态，玻璃态和橡胶态之间称为玻璃化转变区。

图2 割线模量-温度曲线Fig. 2 Secant modulus-temperature curve

1.2 低温拉伸试验

为研究低温对橡胶材料力学性能的影响，本文在温度分别在20 ℃、0 ℃、-10 ℃、-20 ℃、-30 ℃、-40 ℃环境下进行了橡胶材料的单轴拉伸试验。

试验材料为炭黑填充橡胶，胶料编号为FS035A，由中国中车时代新材股份有限公司生产。单轴拉伸试样形状，如图3所示[10]。试样在200T电磁平板硫化机上制备，硫化温度为150 ℃，硫化压力为21 MPa，硫化时间为15 min。试验前试样在环境温度为(23±1)℃的室内调节6 h，室内湿度为50%，试样标距长度为25 mm。

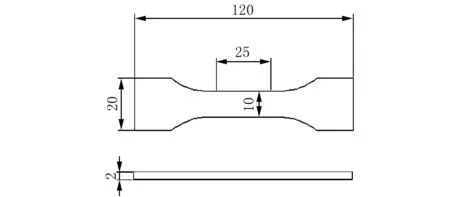
图3 单轴拉伸试样Fig. 3 Specimen for uniaxial tensile experiments

试验在CMT 4204 电子万能试验机上进行，试验温度依次为20 ℃, 0 ℃, -10 ℃, -20 ℃, -30 ℃, -40 ℃，采用液氮进行降温，待温度降至指定温度后保温5～10 min，拉伸速率为6 mm/min，为消除偶然因素的影响，每个温度进行三次实验。

1.3 试验结果分析

试验得出不同温度下的应力应变关系曲线，如图4所示。从图4可以看出，橡胶材料的应力应变关系具有较强的非线性，且随温度的降低，橡胶材料的拉伸弹性模量呈增大趋势。

图4 不同温度下的应力-应变曲线Fig. 4 Stress-strain curves at different temperature

图5所示为橡胶试样在拉伸水平分别为80%、100%、120%、130%、140%、150%时的割线模量-温度曲线。从图中可以看出在各拉伸水平下橡胶材料的

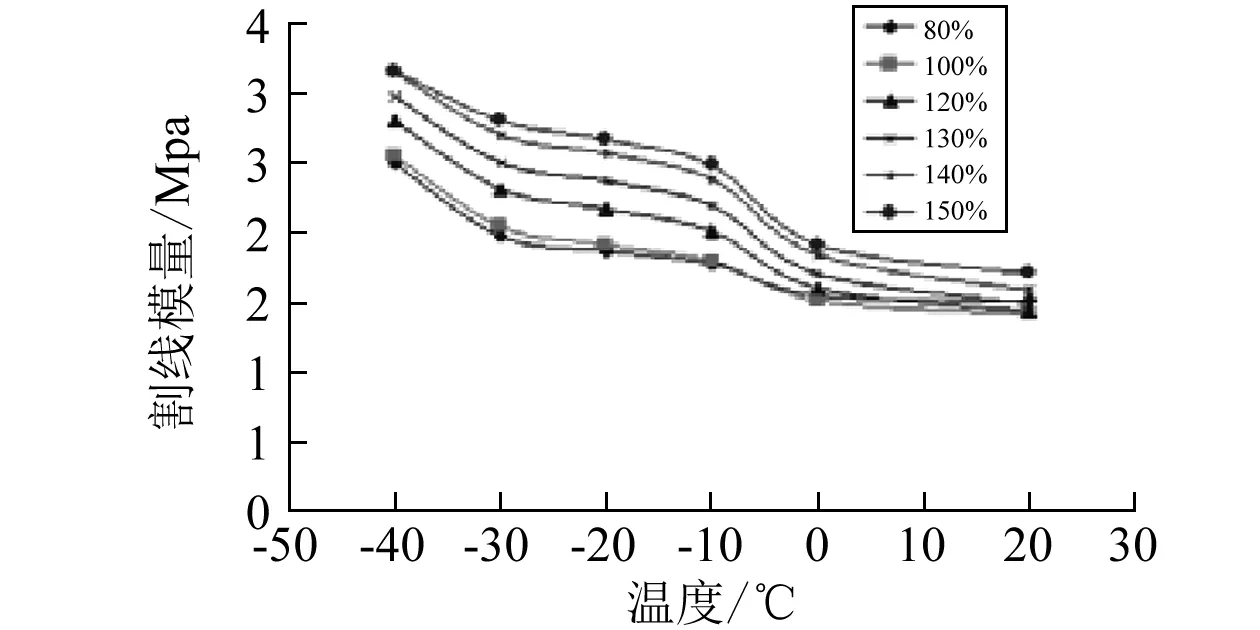
图5 割线模量-温度曲线Fig. 5 Secant modulus-temperature curves

割线模量随着温度的降低总体上呈增大趋势；0 ℃～-10 ℃、-30 ℃～-40℃区间橡胶材料的割线模量变化较大；温度对不同应变水平下的橡胶材料割线模量影响不一致。

2 温度因子

环境温度是影响橡胶弹性元件刚度的一个重要因素。已有的研究表明，在缺乏橡胶材料低温本构模型的情况下，用常温本构参数替代低温本构参数进行弹性元件刚度数值模拟，所预测的刚度与试验相比误差很大，尤其是环境温度低于0 ℃的情况下，因此有必要对预测刚度进行修正。

假设橡胶弹性元件的刚度与环境温度呈一定的函数关系。在相同的工况下，将橡胶材料低温下的本构曲线的割线模量与常温下的割线模量之比定义为温度因子φ，其表达式为

(2)

ΔT=T0-T

(3)

式中：E0为橡胶材料常温T0(20 ℃)下的割线模量，E为橡胶材料在温度为T下的割线模量。

上式中当环境温度为常温时，ΔT=0,φ=1。本文采用多项式函数来描述温度因子，其表达式为

(4)

式中：N为多项式阶数，ai为第i次项系数。

当环境温度T=-40 ℃时， ΔT=60 ℃，显然其幂函数肯定很大，会导致多项式系数非常小，故令

(5)

则温度因子可表示为

(6)

3 橡胶弹性元件低温刚度预测

3.1 锥形簧常温刚度数值模拟

图6所示的锥形橡胶弹簧广泛应用于轨道车辆减振系统，其额定载荷为垂向60 kN，其中芯轴、隔板、外套为45号钢材料，其弹性模量E=210 GPa，泊松比μ=0.3，橡胶材料在常温(20 ℃)时Ogden 3 阶模型参数如表1所示。

表1 Ogden(N=3)模型参数

表中N为Ogden模型阶数；μ、α为Ogden模型参数。

建立如图7所示的某有限元模型，在外套支撑端面施加固定约束，在芯轴中心处建立参考点，将参考点与芯轴孔耦合， 沿Y轴负方向施加大小为60 kN的集中力。利用Hypermsh软件划分网格，然后导入ABAQUS中进行求解分析，导出参考点载荷位移数据，求得在承受60 kN垂向载荷下，锥形簧的刚度为5.68 kN/mm。

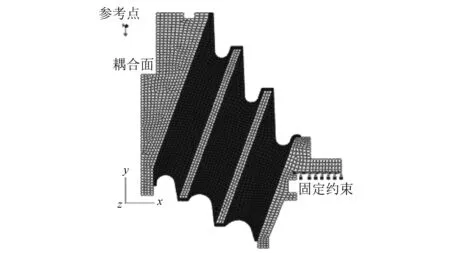
图 7 锥形簧有限元模型Fig. 7 FEA model of cone-shape spring

图8所示为锥形簧橡胶区域的最大主应变等值线图，从图中可以看出主要承受载荷的区域 A 的应变为1.2～1.4。

图8 锥形橡胶弹簧橡胶应变等值线图Fig. 8 Rubber strain contours of cone-shape spring

3.2 温度因子拟合

由于锥形簧主要受载区域的应变为1.2～1.4，那么用于拟合温度因子的材料试验的数据应该处于相同应变水平。提取橡胶试样在拉伸长度分别为120%、130%、140%时的割线模量如表2所示。

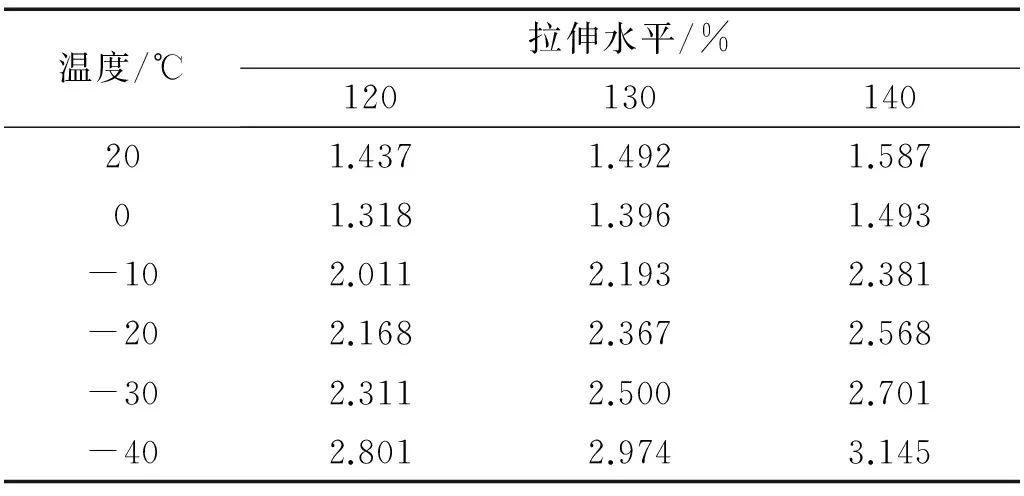
表2 不同温度下的割线模量

通过式(2)、(3)计算试样不同温度下的温度因子，结果如表3所示。

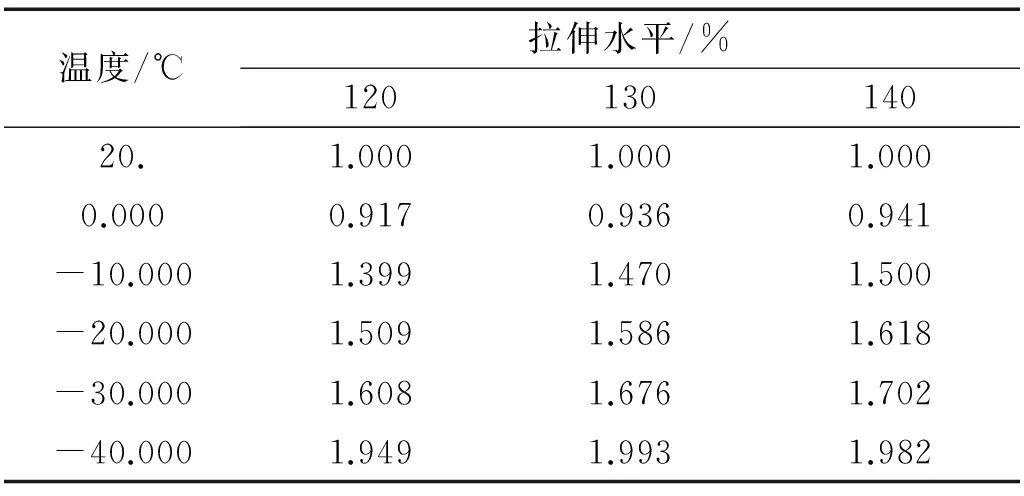
表3 不同温度下的温度因子

同时选择表2中三种应变水平下的实验数据，根据式(6)，分别选择2阶、3阶、4阶多项式进行拟合，拟合结果如表4所示。

表4 温度因子拟合结果

由表4可知，4阶多项式残差最小，拟合效果最好，故温度因子表达式为

φ(x)=0.999 1+1.205 6x+0.086 9x2+
0.020 5x3+0.011 5x4

(7)

3.3 锥形簧低温刚度预测

代入式(7)计算锥形簧低温刚度如表5所示。

表5 刚度预测结果

4 锥形簧低温刚度实验与验证

4.1 低温刚度实验

考虑到残余变形的影响及橡胶材料恢复能力，静刚度试验应先进行高温下的刚度试验再进行低温下的刚度试验，即依次进行0 ℃、-10 ℃、-20 ℃、-30 ℃、-40 ℃下的刚度试验，两次试验之间间隔为1 h。为了消除加工时产生的内应力，锥形簧产品须在(23±2)℃环境温度下停放至少24 h后进行试验，实验前将产品放入低温箱进行降温，待温度降低至各个温度点后保温2 h，施加大小为60 kN的垂向载荷，为去除Mullins效应的影响，循环加载5次，取第4次加载曲线为实验刚度曲线，试验结果如图9和表5所示。

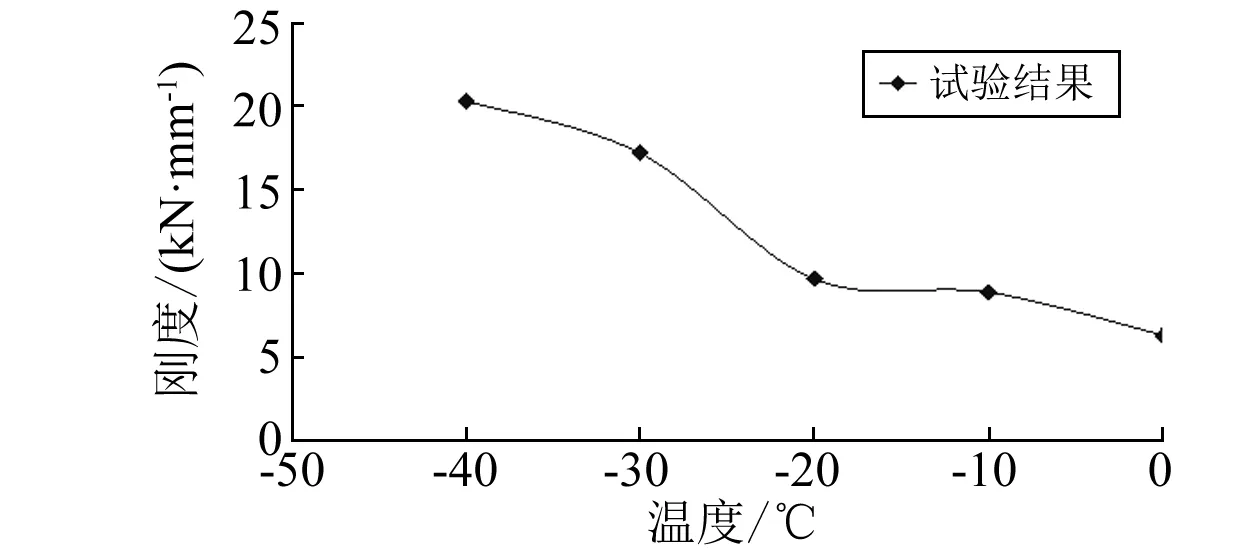
图9 锥形簧低温刚度试验结果Fig. 9 Experiment results of cone-shape spring stiffness at low temperature

从图中可以看出垂向60 kN载荷工况下，随着温度的降低锥形簧产品的刚度呈增大趋势，在-10 ℃～-20 ℃区间产品刚度变化很小，而在-20 ℃～-30 ℃区间产品刚度变化较大。结合图5可以看出产品的刚度-温度曲线与材料试样的割线模量-温度曲线形状不一致。

4.2 误差分析

从表6可以看出当环境温度高于-20 ℃时，本文预测的刚度误差满足工程使用要求，当环境温度≤-30 ℃时误差很大。分析误差产生的原因主要有以下几点：①锥簧产品中含有钢构件，产品的刚度与金属件的结构有关系；②与金属接触硫化到一起的橡胶材料的变形与纯橡胶材料的变形特点不一致；③锥形簧产品在实际工作中主要承受剪切变形，环境温度对橡胶材料的拉伸性能与剪切性能影响是否一致尚不明确，还有待进一步研究。

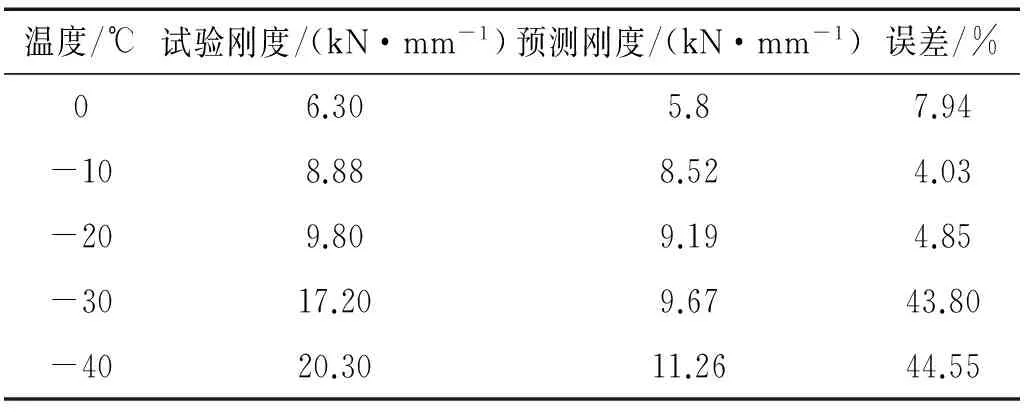
表6 刚度预测误差

5 结 论

(1) 在环境温度分别为20 ℃, 0 ℃, -10 ℃, -20 ℃, -30 ℃，-40 ℃，应变范围为0～150%下对橡胶材料进行单轴拉伸试验，研究应变分别为80%、100%、120%、130%、140%、150%时橡胶本构曲线的割线模量随温度变化的规律，结果表明在各应变水平下橡胶试样的割线模量随着温度的降低呈增大趋势，特别是在0 ℃～-10 ℃、-30 ℃～-40 ℃温度区间，这种趋势更为明显。

(2) 将橡胶试样在低温下本构曲线的割线模量与常温下的割线模量之比定义为橡胶材料的温度因子，构造了温度因子的多项式函数表达形式，并利用橡胶试样拉伸实验数据拟合得到不同应变水平下的温度因子。

(3) 对锥形簧进行常温下的刚度仿真，通过橡胶材料温度因子对锥形簧常温下刚度进行修正，预测其在0 ℃, -10 ℃, -20 ℃, -30 ℃和-40 ℃低温下的刚度，并进行锥形簧产品在常温和低温下的刚度台架试验验证，结果表明环境温度高于-20 ℃时，利用温度因子预测锥形簧刚度误差小于8%，满足工程使用要求，但是当环境温度低于-30 ℃时预测刚度误差较大。

[1] 丁智平，陈吉平，宋传江. 橡胶弹性减振元件疲劳裂纹扩展寿命分析[J]. 机械工程学报，2010，46(22)：58-64. DING Zhiping，CHEN Jiping，SONG Chuanjiang. Analysis of fatigue crack growth life for rubber vibration damper[J]. Journal of Mechanical Engineering，2010，46(22)：58-64.

[2] MARS W V，FATEMI A. A literature survey on fatigue analysis approaches for rubber[J]. International Journal of Fatigue，2002，24(9)：949-961.

[3] SAINTIER N，CAILLETAUD G，PIQUES R. Multiaxial fatigue life prediction for a natural rubber[J]. International Journal of Fatigue，2006，28(5)：530-539.

[4] 上官文斌，吕振华. 汽车动力总成橡胶隔振器弹性特性的有限元分析[J]. 内燃机工程，2003，24(6)：50-55. SHANGGUAN Wenbin，LÜ Zhenhua. Finite element analysis of elastic characteristics of rubber isolator for automotive powertrain systems[J]. Chinese Internal Combustion Engine Engineering，2003，24(6)：50-55.

[5] 袁东野. 寒区桥梁板式橡胶支座低温性能研究[D]. 哈尔滨：东北林业大学，2013.

[6] 余惠琴，刘晓红. 低温改性天然橡胶剪切性能研究[J]. 固体火箭技术，2006，29(3)：222-224. YU Huiqin，LIU Xiaohong. Study on shear properties of low-temperature modified nature rubber[J]. Journal of Solid Rocket Technology，2006，29(3)：222-224.

[7] 王付胜，高新文，曹江勇，等. 轨道车辆用耐低温橡胶减振元件的研究[J]. 铁道车辆，2012，50(11)：22-25. WANG Fusheng，GAO Xinwen，CAO Jiangyong，et al. Research on low temperature resistant rubber damping elements for rail vehicles[J]. Rolling Stock， 2012，50(11)：22-25.

[8] 由世岐，刘斌，楼永林. 低温环境对叠层橡胶支座变形特性影响的试验研究[J]. 东北大学学报(自然科学版)，2005，26(3)：297-299. YOU Shiqi，LIU Bin，LOU Yonglin. Low-temperature effect on deformation behavior of laminated rubber isolators[J]. Journal of Northeastern University(Natural Science)，2005，26(3)：297-299.

[9] 王涛. 常温和超低温橡胶金属复合密封机构的有限元分析与优化[D]. 哈尔滨：哈尔滨工业大学，2007.

[10] 卜继玲，黄友剑. 轨道车辆橡胶弹性元件设计计算方法[M]. 北京：中国铁道出版社，2010：41-63.

Stiffness prediction of rubber springs at lower temperature

DING Zhiping1， MU Longhai1， BU Jiling2， HUANG Youjian2， ZENG Jiaxing1

(1. School of Mechanical Engineering，Hunan University of Technology，Zhuzhou 412007，China；2. Zhuzhou Time New Material Technology Co., Ltd.，Zhuzhou 412007，China)

Uniaxial tensile tests were conducted on rubber specimens at 20 ℃, 0 ℃, -10 ℃, -20 ℃, -30 ℃ and -40 ℃ and the change of secant modulus of the rubber material’s constitutive curve with the variation of temperature was studied under different strain levels. The temperature factor was defined as the ratio of the secant modulus of rubber specimen’s stress-strain curve at low temperature to that at room temperature and was expressed as a polynomial function. The temperature factors under different strain levels were obtained by fitting the rubber specimen tensile test data. The stiffness of a conical spring at room temperature was simulated and then modified by the temperature factors to predict the stiffness of cone-shape springs at low temperature. The stiffness bench tests of spring products at room temperature and low temperature were carried out, and the results show that the error of predicted stiffness is within 8% which can meet the project requirements when the ambient temperature is higher than-20 ℃, but when the ambient temperature is lower than-30 ℃ the error will be increased.

rubber spring；uniaxial tensile；stiffness at low temperature；temperature factor；prediction

中央财政创新团队专项资金项目(0420036017)

2016-03-03 修改稿收到日期： 2016-05-17

丁智平 男，博士，教授，1956年生

TQ332；TQ328.3

A

10.13465/j.cnki.jvs.2017.14.010