一种高聚类幂律可调网络异质配置模式下的公共品博弈研究

苗 萍，杨洪勇

(鲁东大学信息与电气工程学院，山东 烟台 264025)

一种高聚类幂律可调网络异质配置模式下的公共品博弈研究

苗 萍，杨洪勇

(鲁东大学信息与电气工程学院，山东 烟台 264025)

为了研究网络结构与演化博弈之间的关系，提出了一种基于网络内部“三角结构”与“内部演化”演化机制的高聚类幂律可调的网络模型。该网络模型具有无标度网络幂律分布的特性，且具有更高的聚类系数。在该网络模型的基础上，研究了异质配置模式的公共品博弈，即根据网络中的节点与其一层邻居和二层邻居中合作者数目的多少来决定公共品博弈中合作者的投入差异，并通过一个调节因子来调节投入差异的异质性程度。最后仿真证明，该异质配置模式演化博弈模型在高聚类幂律可调网络模型上可以快速达到纳什均衡，且存在一个调节因子的最佳范围能够促进合作的涌现。

高聚类系数；幂律可调；异质配置；演化博弈

0 引言

理解网络结构和动态演化特性之间的关系是复杂网络的研究方向之一。“WS小世界网络”具有较高的聚类系数[1]，“BA无标度网络”节点的度服从幂律分布的特性[2]，现在许多文献对这两个经典网络模型进行了深入的研究。但是现实世界中的网络一般同时具备高聚类无标度的特性，因此Holme与Kim提出了同时具备高聚类和无标度特性的HK网络模型[3]。然而在HK网络模型的构造过程中，网络中新加入的节点只与网络中已存在节点之间建立连接。本文从实际出发联合考虑到网络的“内部演化”与“三角结构”，提出了一种幂律可调的网络模型，该网络模型在服从幂律分布且幂律可调的情况下，相对于HK网络具有更高的聚类系数。

1 网络模型的构建

1.1 网络模型内部演化机制

假设在已知网络中加入一个新节点，网络中已经存在的节点i被选中连接的概率服从：

(1)

其中,ki为i节点的度，∑kj为网络中所有节点的度之和，本文所提出的高聚类幂律可调网络内部演化模型构建过程如下：

1) 初始状态: 初始网络中含有m0个完全相连接的节点。

3) 终止条件: 网络的规模N达到预先设定的值。

1.2 演化网络度分布分析

(2)

(3)

解微分方程(3)得：

(4)

则

(5)

因此：

(6)

则该网络模型的幂律指数γ为

(7)

由于概率p∈[0,1]，通过式(7)可得当p=0时，该网络模型的幂律指数γ=3则网络回归到BA无标度网络。当p=1时γ=5-4/(m+1)因此该网络为幂律指数大小介于γ=3和γ=5-4/(m+1)之间的幂律可调网络模型。且p是新加入的节点的边选中以式(1)连接的某点的邻居的概率，p的值影响了网络中形成三角结构的数量即该网络中三角回路的数量。由于内部演化机制的存在，使得网络中的三角回路的数量呈倍数增长，这种网络结构对论文后半部分研究的异质配置模式公共品演化博弈有重要影响。

1.3 仿真分析

复杂网络中某点i的聚类系数可表示为

(8)

其中,n为节点i的所有相邻节点之间相互连接的边的个数，k为节点i的所有相邻的节点的个数，即节点i的邻居。本文提出的高聚类幂律可调网络模型，由于内部演化机制的存在，网络新边的产生不只存在于新旧节点之间，也存在于被当作某中心节点的邻居而选中的旧节点与该中心节点的其他邻居之间，根据式(8)可知，该网络模型的聚类系数将大大提升。

图1的实验结果显示了本文提出的高聚类幂律可调网络模型的聚类系数与HK网络模型聚类系数的比较，初始条件中网络中原有节点数m0为8, 每次引入新节点时与新节点连接的边数m为6，最终生成网络的规模N=1 000，由仿真结果可以看出，随着调节概率p的增加，网络的聚类系数单调地增加，在相同的调节概率下，由于旧节点之间同时产生新边的内部演化机理，高聚类幂律可调网络的聚类系数远远高于HK网络的聚类系数。

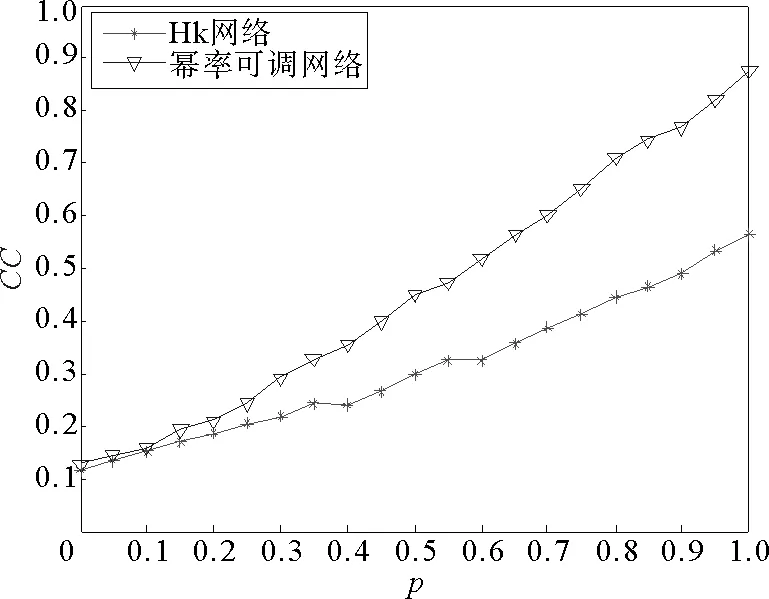
图1 聚类系数比较Fig.1 Comparison of clustering coefficients

2 异质配置模式公共品博弈

2.1 复杂网络上的公共品博弈

假设在一个公共品博弈中，参与者总数为N,每个参与者独立地决定是否以代价c在公共品博弈中进行投资，且总体回报能够增值r(r>1)倍，博弈完成之后的总体回报会全部平均分给所有参与者[9]。则合作者的收益PC与背叛者的收益PD可表示为：

(9)

从整体来看，由于背叛者的收益总是高于合作者的收益，如果博弈持续下去，所有的参与者将都不会进行投资，因而所有参与者将都不会有收益，从而导致公共悲剧。但如果所有的参与者都进行投资那么所有的参与者都能获得最高报酬。为了防止这种公共悲剧的发生，更好地促进每个参与者参与合作，达到纳什均衡时参与者都有较大的收益，本文提出了以下异质配置模式的公共品博弈模型。

2.2 异质配置模式公共品博弈模型

假设公共品博弈中每个个体i参与由自己和ki个邻居组成的ki+1次公共物品博弈，并以资金量Q进行投资。则i从邻居j中获得的收益可表示为

(10)

则i点所参与的由自己和ki个邻居组成的ki+1次公共物品博弈获得的总收益的表达式为

(11)

当β=0时，合作者的投入量不受调节因子的影响均为C，该演化博弈模型为投入均质模型。当β≠0时合作者依靠调节因子β来调节投入异质性的强弱。得到收益和之后，所有个体随机选取一个邻居按照Fimi演化规则决定是否采取该邻居的策略[10]。如每轮博弈完成之后，总收益为Pi的i个体是否采取随机选取的总收益为Pj的i点的邻居j的策略的概率服从：

(12)

其中,k刻画了参与者的非理性程度，当k→0时表示参与者为完全理性，该参与者只会学习自身的博弈策略。本论文中的所有仿真程序k的值均为0.1，初始时，背叛者与合作者的比例均占50%。

2.3 仿真分析

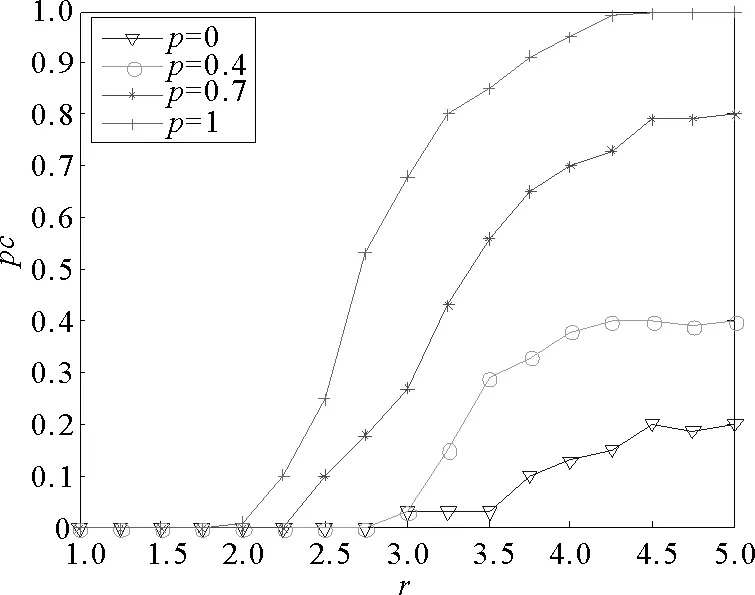
图2 合作概率的变化Fig.2 Change of cooperation probability

2.3.1高聚类幂律可调网上均质公共品博弈

由式(10)可得当调节因子β=0时，个体的投入资金量为固定值C，即可得到投入均质模型，在该高聚类幂律可调网络上通过改变网络构造过程中的可调概率p，观察网络结构的变化对投入均质模型的影响，其仿真结果如图2所示。

仿真实验是在N=1 000的网络上博弈200次取最后50次平均得到的，仿真结果显示在增益因子r比较小的情况下，演化博弈的合作概率pc结果为0，随着增益因子的增加，合作比率呈线性增长最后趋于稳定。由于在该网络构造过程中，当概率p=0时，网络回归到BA网络，由仿真结果看出博弈达到稳定后合作概率较低，且达到稳定状态需要较大的r值。随着p的逐渐增加，网络的聚类系数随之增大，且网路中三角形回路的数量不断增加，从而形成结构上的反馈机制。文献[11]证明HK网络中的三角形回路能够促进网络演化博弈个体的合作。所以在增益因子r相同的情况下，p越大对应的合作概率就越高。

2.3.2高聚类幂律可调网络上异质公共品博弈

当式(10)中调节因子β≠0时，每个合作者投入资金量C受调节因子β的影响不再是固定值，而是根据某节点与邻居节点，邻居节点与二层邻居节点中合作者占参与者的比重来决定。因为资金配置过于异质或者过于均匀都会抑制合作，为了保证参与者在这种外在强制调节的干预下，资源配置在量上对每轮公共品博弈的收益达到最优，经过反复试验发现，调节因子β应合理地限制在(0,1]中。

图3表示调节因子与合作概率的关系，当β控制在(0,1]时，随着r的增长，pc与r之间呈现出一种平缓的正相关关系，r值越大越能够维持合作者的生存，合作概率不断提高，且能快速达到稳定状态。当β超出(0,1]的范围时，r的差异对该演化博弈的影响逐渐变小，随着β的不断增加，最终不同的r值具有相似的合作水平。

由图4的结果可以看到，在网络状况相同情况下，随着增益因子的增加，异质配置模式公共品博弈可以较同质配置模式公共品博弈更快速到达纳什均衡稳定状态，且出现合作涌现。基于以上结果分析，当β≠0时，若要增加收益，网络中个体基于目前一层邻居与二层邻居中合作者数目的比例来进行投资。由于β控制在(0,1]之内，若合作者与参与者之比≥0.5说明社团中有较多的合作者，β取(0,1]，这种强制干预调节使得合作者占参与者的比重在原始基础上增加，从而参与者的每轮博弈获得比不加强制调节之前更高的收益，网络中的个体更趋向于选择合作，进而提高了合作概率。若合作者与参与者之比<0.5说明相应节点范围内有较少的合作者，β取其相反数，同样通过这种强制调节，使得合作者占参与者的比重>1，参与者的每轮博弈同样获得比不加强制调节之前更高的收益，进而这种调节作用使得合作者投资量不断增加，其邻居获得的收益量随之增加。由于个体收

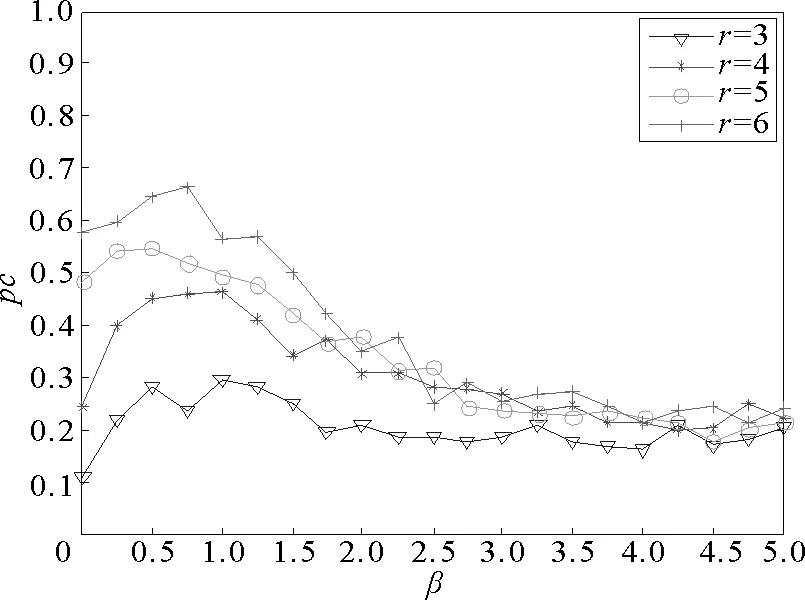
图3 合作概率的变化Fig.3 Development of cooperation probability

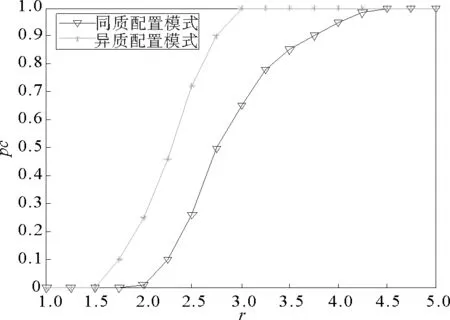
图4 博弈结果结果比较Fig.4 Comparison of game results

益同时受一层邻居和二层邻居的影响，该高聚类幂律可调网络中存在大量三角形回路，如果三角形两个顶点上的参与者均为合作者那么他们可以通过另一个顶点作为共同的邻居具有式(11)的收益关系，从而获得额外的收益，因此该网络的高聚类特性使得中心节点与一层邻居和二层邻居之间产生结构上的正反馈互惠机制，降低了合作策略扩散的阈值，使得演化博弈继续进行的过程中有更多的个体趋向于合作。

图5显示了该演化博弈策略的空间动态斑图，其中浅色代表合作个体，深色代表背叛个体。从图中可以看出，随着演化博弈的进行，合作者的合作簇不断扩散，背叛者的簇逐渐消减，直至合作者几乎占据整个博弈空间(见图5d)。由于度较大的的节点每轮博弈后的累计收益一般会比小度节点高，所以如果中心节点采用合作策略，又由于资金投入调节机制的存在，其收益会随着邻居中的合作者数目增加而提高，从而促使更多邻居采用中心节点的策略而转变为合作者，同时邻居中合作者数目的提高又会使得中心节点的收益提高，进而形成了采用合作策略的中心节点的收益与其邻居策略选择间的正反馈机制。

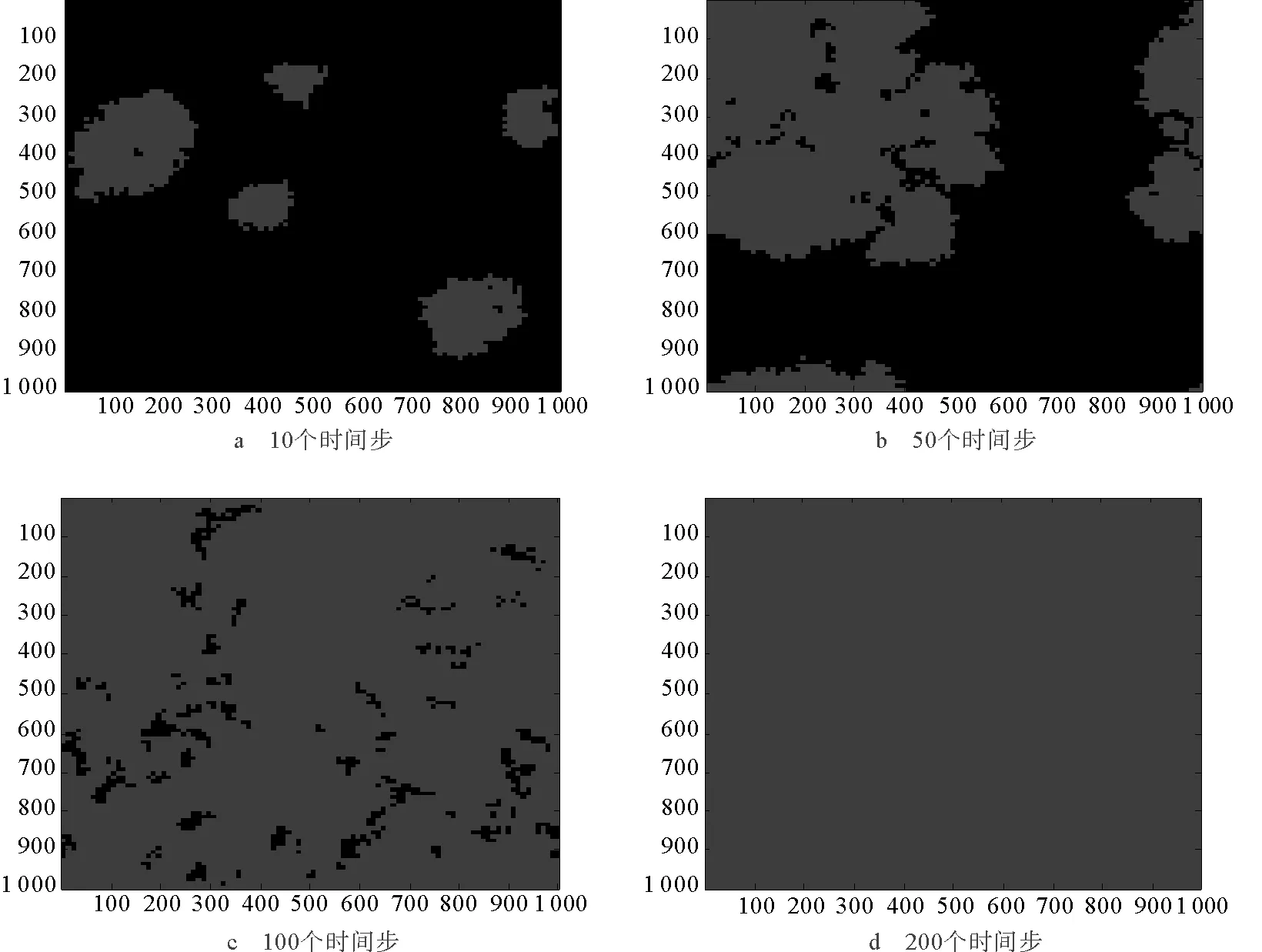
图5 空间斑图Fig.5 Space pattern

3 结论

本文基于“三角结构”与“内部演化”机制，提出了一种高聚类幂律可调的网络结构模型，该模型的高聚类特性会使得中心节点与邻居节点之间产生结构上的正反馈互惠，降低了合作策略扩散的阈值；并在此基础上提出了一种通过调节因子来调节公共品博弈中合作者比例来控制投入差异的异质配置模式公共品博弈，实验证明在该高聚类幂律可调网络上进行异质配置模式公共品博弈，存在调节因子∈[0,1)使得博弈快速达到纳什均衡，促进合作的涌现。

[1] Watts D J,Strogatz S H. Collective dynamics of small-world networks[J]. Nature, 1998, 393(3): 440-442.

[2]Barabási A L, Albert R,Jeong H. Mean-field theory for scale-free random networks[J]. Physica A Statistical Mechanics & Its Applications, 1999, 272(1/2): 173-187.

[3]Holme P, Kim B J. Growing scale-free networks with tunable clustering[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2001, 65(2): 95-129.

[4]Huang Z G,Wu Z X,Wu A C,et al. Role of collective influence in promoting cooperation[J]. Europhysics Letters, 2008, 84(5): 786-798.

[5]Yang H X,Wu Z X,Du W B. Evolutionary games on scale-free networks with tunable degree distribution[J]. Europhysics Letters, 2012, 99(99): 288-290.

[6]Yang H X,Wang W X,Wu Z X, et al. Diversity-optimized cooperation on complex networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2009, 79(2): 711-715.

[7]Li Z,Deng C,Suh I H. Network topology control strategy based on spatial evolutionary public goods game[J]. Physica A Statistical Mechanics & Its Applications, 2015, 432: 16-23.

[8]Chen M H,Wang L,Sun S W,et al. Evolution of cooperation in the spatial public goods game with adaptive reputation assortment[J]. Physics Letters A, 2015, 380(1): 40-47.

[9]Colman A M. Game theory and its applications in the social and biological sciences[J]. Journal of Behavioral Decision Making, 1998, 11(3): 228-229.

[10] Gyö, Szabó R, Toke A C. Evolutionary prisoner's dilemma game on a square lattice[J]. Physical Review E, 1998, 58(1): 69-73.

[11] Rong Z,Yang H X,Wang W X. Feedback reciprocity mechanism promotes the cooperation of highly clustered scale-free networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2010, 82(2): 1922-1928.

(责任编辑 李进)

Donation-Diversity Public Goods Game on High Clustering Coefficient and Adjustable Power-Law Networks

MIAO Ping, YANG Hongyong

(School of Information and Electrical Engineering, Ludong University, Yantai 264025, China)

In order to study the relationship between network structure and evolutionary game,a high clustering coefficient and adjustable power-law network model is put forward on the basis of the “triangular structure” and “internal evolution” evolution mechanism in the network. This model possesses the same characteristics as the standard scale-free networks such as the power-law degree distribution, but with the high clustering at the same time. And on the basis of the network model, according to the numbers of cooperators that is in a node with it’s immediate neighbors and neighbors’ neighbors to determine the difference of cooperators’ inputs in public goods game, in the same time use a regulatory factor to adjust the degree of heterogeneity. The simulation proves that the heterogeneous configuration model can quickly reach the Nash equilibrium, and the adjustment factors exist an optimal range can promote the boom of cooperation on the new network model.

high clustering coefficient; adjustable power-law; heterogeneous configuration; evolutionary game

1672-3813(2017)02-0052-07；

10.13306/j.1672-3813.2017.02.008

2016-07-09；

2016-12-02

国家自然科学基金(61273152,61673200)；山东省科技发展计划(2012YD03110)

苗萍(1990-)，女，山东泰安人，硕士研究生，主要研究方向为复杂网络、博弈论。

杨洪勇(1967-)，男，山东德州人，博士，教授，主要研究方向为复杂网络、多智能体编队控制等。

N94; F224

A