基于GWR的大兴安岭森林立地质量遥感分析*

2017-07-18李明泽郭鸿郡范文义

林业科学 2017年6期

关键词：局域植被指数全局

李明泽郭鸿郡范文义甄贞

(东北林业大学林学院哈尔滨 150040)

基于GWR的大兴安岭森林立地质量遥感分析*

李明泽郭鸿郡范文义甄贞

(东北林业大学林学院哈尔滨 150040)

立地质量；多光谱遥感；地理加权回归模型；多元线性回归模型

立地，在生态学上又称“生境”，是指森林或者其他类型植被生存的空间及与之相关的自然因子的综合(马建路等，1993)。森林的生长状况和生产力与森林的立地环境及其质量密切相关，为了更好地掌握森林状况并进行经营管理维护，需要对森林立地质量进行评价，以反映出森林立地的宜林性或潜在的生产力，从而量化立地的生产潜力(Skovsgaardetal.， 2008)，为合理进行森林经营管理提供客观依据。

在林业实际生产中，通常采用树高来评价立地质量(骆期邦等，1989)，而根据采用的树高不同又可以分为立地指数法和地位级指数法。在立地指数法中，基准年龄下的林分优势木平均高即立地指数(site index,SI)(相聪伟，2010)，而在地位级指数法中，基准年龄下的林分平均高即地位级指数(site class index,SCI)(王鹤智，2012)。在立地指数研究方面，Carmean(1978)采用多元统计构建数学模型，提取立地因子来拟合立地指数，对立地质量进行间接评估，这种方法具有完备的理论体系，并且能够有效解决传统方法中有林地和无林地以及多树种统一评价的问题，因而被广泛使用；但是在利用传统回归模型(全局模型)时，都是以忽略数据的空间变异为前提的，也就是说传统的回归模型实际上在分析之前就假定变量间具有同质性，从而掩盖了变量间关系的局部特性，所以结果也只是研究区域内的某种“平均”(刘畅，2014)。在地位级指数研究方面，多采用传统样地调查法或者利用传统的统计模型进行拟合来预估森林的立地状态，然而这2种方法都无法解决空间上的不连续和自相关问题。

为了探究数据的空间关系，Brundon等(1998)基于局域光滑理论提出了地理加权回归(geographically weighted regression，GWR)模型。GWR模型在回归参数中加入了空间信息，在每个观测点上根据一个权函数来进行参数回归，每个观测点都有一个与之相对应的模型，能够直观显示数据的空间非平稳性，即每个样地点上参数随着空间的变化而变化(Curtetal.， 2001；Louwetal.， 2002)，因此该方法广泛应用于诸多领域，在林学方面也得到了较好应用，如Zhen等(2009)利用GWR模型结合凉水实验林场风倒木数据建立了风倒木发生概率、数量以及倒木蓄积预估模型，刘畅(2014)基于GWR模型和最小二乘回归相互参照的方法建立了黑龙江省碳储量预估模型。

现代遥感技术和地理信息科学的迅猛发展，使得人们能够获得更为精准的立地信息，同时也能够对林地质量和立地因子之间的相互作用有更深入的了解，提高了立地质量评价的客观性，能够实现立地质量评价的自动化。马明东等(2006)利用多元线性回归方法结合Landsat TM影像对四川省镇关江流域森林立地情况进行了分析；巩垠熙等(2013)采用人工神经网络结合多光谱遥感数据完成了内蒙古旺业甸林场森林立地质量评价；李龙等(2016)基于研究区的实地采样数据，结合遥感等技术，采用GWR模型对土壤有机碳密度及其影响因子进行拟合，探究了不同环境因子对土壤有机碳密度影响的空间变异特性。

大兴安岭是我国目前连片面积最大的国有林区，经营面积达8.35万km2,是我国东北的“粮仓”和华北平原的天然屏障，拥有丰富的林木资源，急需一种有效、可行的方法对该区域的地位级指数分布状态进行评价。鉴于此，本研究以地位级指数值作为立地质量优劣的评价指标，利用大兴安岭地区森林资源一类清查数据计算SCI，并结合遥感因子和林地调查因子，建立以传统最小二乘回归和GWR 2种方法构建的地位级指数模型，在对比2种方法预估地位级指数有效性的基础上，选取效果较好的方法绘制SCI空间分布图，从而定量估测、评价大兴安岭地区的森林地位级指数，以期为该区域的森林经营管理和营林造林提供一定的数据支持与理论依据。

1 研究区概况与数据预处理

1.1 研究区概况

大兴安岭地区位于黑龙江省、内蒙古自治区东北部，地理坐标为121°12′—127°00′E，50°10′—53°33 N′。全区地形总势呈东北—西南走向，属浅山丘陵地带，平均海拔573 m。冬寒夏暖，昼夜温差较大，年均气温-2.8 ℃，最低温度-52.3 ℃，无霜期90～110天，年均降水量746 mm，属寒温带大陆性季风气候。大兴安岭为多年冻土带，森林土壤类型主要有棕色针叶林土、暗棕壤、灰黑土、草甸土、沼泽土，主要树种有兴安落叶松(Larixgmelinii)、樟子松(Pinussylvestrisvar.mongolica)、红皮云杉(Piceakoraiensis)、白桦(Betulaplatyphylla)、蒙古栎(Quercusmongolica)、山杨(Populusdavidiana)等。

1.2 森林样地数据收集与地位级指数计算

数据来源于2010年国家森林资源一类清查数据，共计526块样地，随机选取108块样地，不参与建模，用于模型精度检验。样地调查内容包括树种组成、林分类型、优势树种、平均年龄、平均胸径、平均树高、株数、断面积、郁闭度等。地形因子由采用1∶50 000地形图矢量化得到的10 m分辨率数字高程模型数据提取，包括海拔、坡度、坡向等。其中林分平均高是在树高曲线上与林分平均直径相对应的树高，在外业测定时通过选取3～5株与林分平均直径接近的树高值加权得到。本研究采用2010年黑龙江省(市、县)林区主要林分类型收获表标准来计算森林地位级指数(引自黑龙江省地方标准，由黑龙江省质量技术监督局于2010年发布)。地位级指数为该林分基准年龄下林分平均高，公式(王鹤智，2012)如下：

(1)

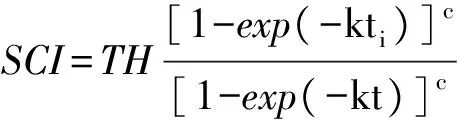
(2)

式中：TH(tree hight)为林分平均高(m);ti为基准年龄(a);k、c为模型参数。

1.3 遥感数据收集及光谱信息和纹理信息提取

选取2010年生长季期间(6—9月)覆盖大兴安岭全部的Lansat-7 TM遥感影像共计12景，影像质量良好，排除大量云层与阴影，对图像进行大气校正后镶嵌、裁剪，最终得到覆盖整个研究区的遥感图像。

根据文军等(1997)研究结果，得到4种植被指数：归一化植被指数(normalized differential vegetation index,NDVI)、土壤修正植被指数(modified soil vegetation index,MSVI)、差值植被指数(difference vegetation index,DVI)和比值植被指数(ratio vegetation index,RVI)；计算得到TM影像6个波段灰度值；计算TM影像灰度共生矩阵(3×3窗口，步长为1)得到6个波段在对角线方向的纹理信息共计48个波段。其中4种植被指数计算公式如下。

归一化植被指数：

NDVI=(band4-band3)/(band4+band3)。

(3)

土壤修正植被指数：

(4)

式中：L取值为0.5。

差值植被指数:

DVI=band4-band3。

(5)

比值植被指数：

RVI=band4/band3。

(6)

式中：band 3为Landsat-7 TM影像第3波段；band 4 为Landsat-7 TM影像第4波段。

2 研究方法

2.1 模型变量的选择与拟合

在显著性水平α=0.05下通过逐步回归筛选出最优自变量因子，最终通过检验的因子有MSVI、DVI、林分平均胸径(average diameter at breast height,ADBH)、林分郁闭度(forest canopy closure,FCC)。已有研究表明，NDVI对于立地质量的空间分布具有较强相关性，且修正土壤干扰的MSVI更能反映立地质量(马明东等，2006)，而DVI能够将植被和其他地类区分开来。肖兴威(2004)证明了林木胸径在林分结构中发挥着重要作用，康冰等(2009)研究表明林分密度对于林分平均高具有较强相关性，所以MSVI、DVI、ADBH和FCC可以作为影响地位级指数分布的变量进行研究。因变量与自变量的描述性统计如表1所示。

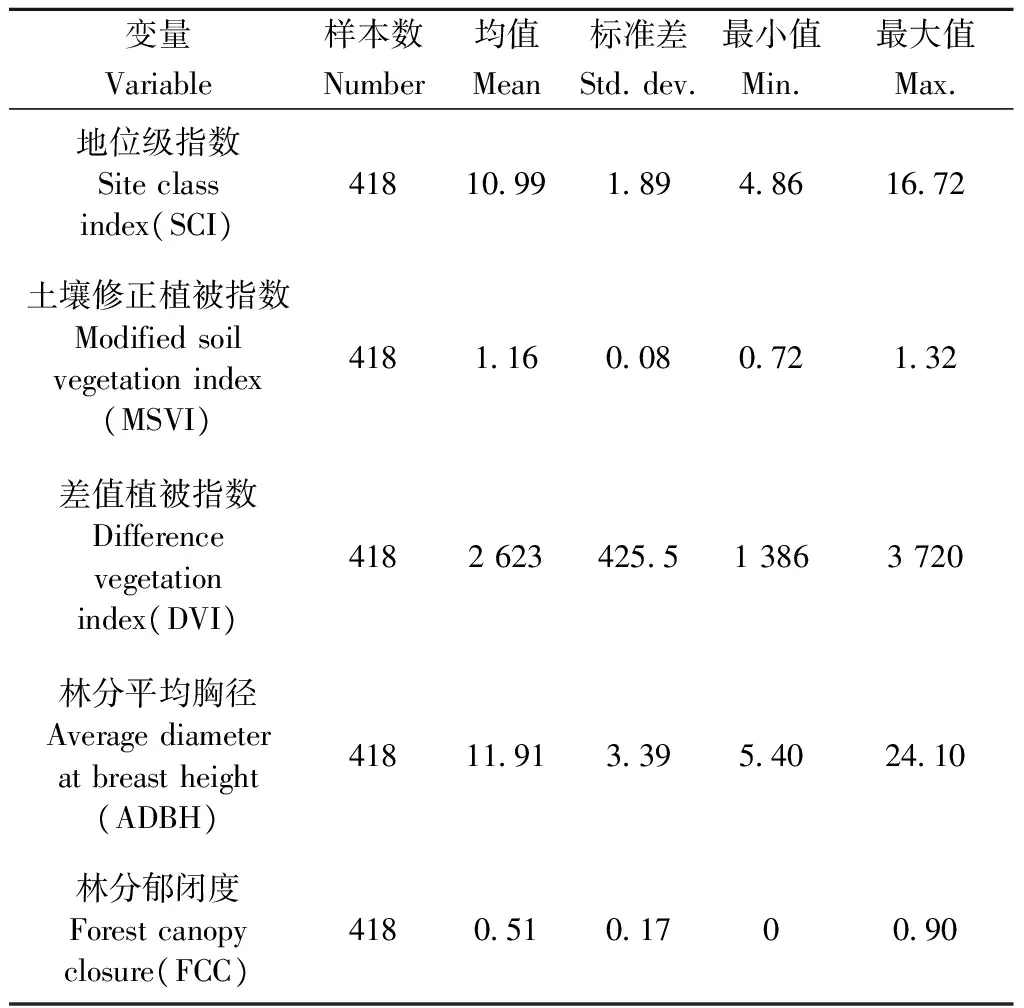
表1 用于本研究拟合变量的描述性统计Tab.1 Descriptive statistics of fitted variables used in this study

郁闭度和林分平均胸径模型采用SPSS19.0软件径逐步回归方法建立。研究区内418块样地参与建模，108块样地用于精度检验。选取59个遥感变量因子用于模型回归，对参与建模的全部自变量因子在显著性水平α=0.05下进行逐步回归并拟合模型，建模结果如式(7)、(8)所示：

FCC=0.97+0.026x1+0.103x2+0.204x3-

1.983x4-0.054x5-0.042x6-0.031x7；

(7)

ADBH=7.666+1.237z1-0.169z2-0.013z3-

0.601z4+1.581z5-0.176z6-0.032z7-

0.01z8+1.968z9。

(8)

模型的拟合统计量见表2，郁闭度模型回归系数见表3，林分平均胸径模型回归系数见表4。经检验，FCC模型的拟合精度为85%，ADBH模型的拟合精度为83%。

表2 模型拟合统计量Tab.2 Fitting statistics of the models

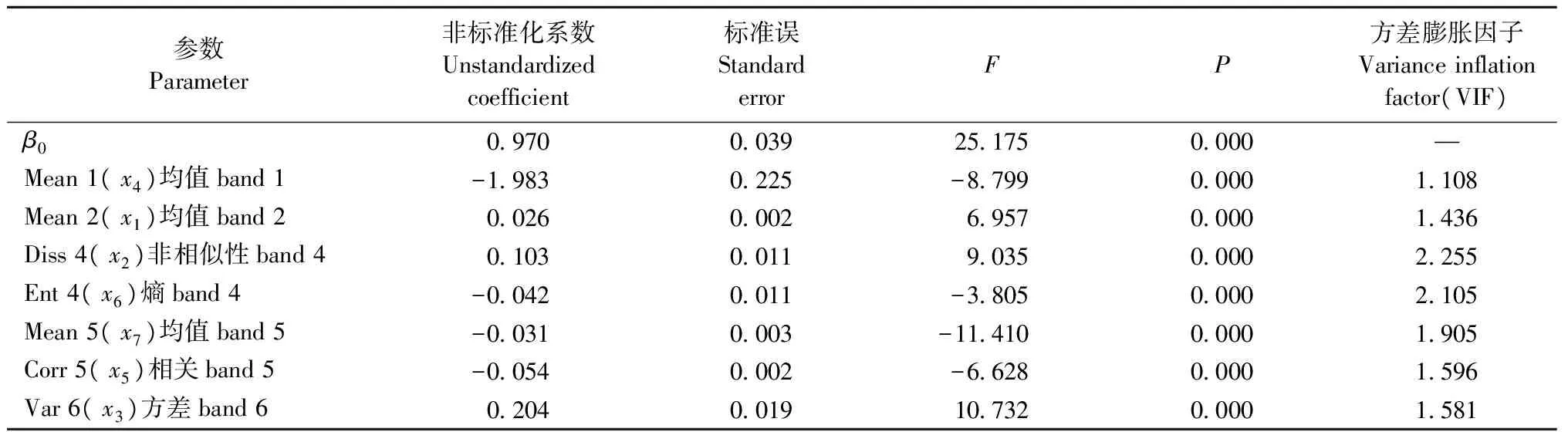
表3 郁闭度模型回归系数Tab.3 Model coefficient estimates of the FCC model

表4 林分平均胸径模型回归系数Tab.4 Model coefficient estimates of the ADBH model

2.2 地位级指数模型构建

2.2.1 多元线性回归统计模型本研究中，因变量是地位级指数，自变量是遥感因子和林分因子。因变量为随机变量，用符号Y表示，自变量通常有多个，用符号X表示。那么因变量Y与自变量X之间的关系用线性回归模型可表示为：

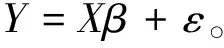
(9)

式中：β为利用最小二乘原理估计出的模型系数向量；ε为模型残差向量，服从正态分布N(0，σ2)。

2.2.2 GWR模型 GWR模型是传统回归方法的扩展，能够进行局部参数估计，其本质是为数据集中的各要素建立独立方程。对于研究区内每个因变量的参数估计，都由1个或者多个自变量结合样本信息的空间关系构成的空间权重综合影响得到。根据地学第一定律，越接近的观测点数据贡献越多的影响，GWR模型以一个距离的衰减函数来进行加权，函数的回归系数即是观测点地理位置的位置函数。GWR模型的结构表达式如下：

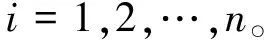
(10)

式中：Yi为因变量地位级指数；(ui,vi)为第i个采样点的坐标(如经纬度)；βk(ui,vi)为第i个采样点上第k个回归参数，是地理位置的函数；ε为误差项。

2.3 全局模型与局域模型的比较

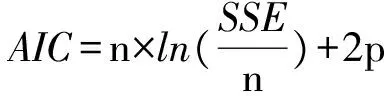
(11)

式中： SSE为残差平方和；n为观测值个数；p为模型参数个数。

模型残差即观测值与估计值之差。传统统计模型的假设条件要求模型残差之间相互独立，本文对于残差空间自相关性的研究采用空间相关性指数莫兰指数(Moran I)，其表达式如下：

(12)

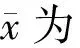
全局Moran I能够揭示研究区内整体的空间自相关性，但如果需要检验每块样地上的空间自相关性是否显著，就需要将全局Moran I局域化，即局域Moran I，其表达式如下：

(13)

wij通常被称为空间权重，其实质是一个随着空间距离增加而逐渐衰减的单调递减函数(覃文忠，2007)。目前最常用的有高斯函数法(Gaussian)和截尾型函数法(bi-square)2种，具体表达式如下。

Gaussian函数法：

(14)

bi-square函数法：

(15)

式中：b为描述权重与距离之间函数关系的非负递减函数，称为带宽(band width)，模型参数估计和模型预测准确度在很大程度上取决于带宽的选择；dij为样地点与其相邻点之间的距离，常被定义为欧式距离：

(16)

本研究采用标准正态检验(standard normal test)来判定模型残差的空间分布是否随机。对于全局模型和局域模型分别计算全局Moran I，并设定Moran I为零时残差分布完全空间随机。如果正态检验得到结果-1.96≤Z≤1.96，则P>0.05(α=0.05)，表示接受零假设，即模型残差的空间分布模式很可能是随机空间产生的结果；若Z>1.96或者Z<-1.96，则P<0.05，则拒绝零假设，即模型残差的空间分布模式不是随机过程产生的。

2.4 模型精度评价

为保证数据的相对独立性，随机抽取森林地位级指数测定结果108个样地点，对模型模拟结果与实际测定结果进行精度对比分析，定性判断模型模拟的总体效果。

2.5 方法实现

采用SPSS19.0软件建立全局地位级指数预估模型，并对模型拟合精度进行评价。使用GWR4.0软件进行模型拟合，使用adaptive bi-square核函数并采用golden section search作为最佳带宽的选择方法，评价标准选择AICc。通过Excel宏文件ROOKCASC来计算全局Moran I和局域Moran I。

3 结果与分析

3.1 预测变量的空间分布

利用ArcGIS软件对模型所选变量进行空间可视化分析，图1为4个预测变量(MSVI、DVI、ADBH、FCC)的空间分布情况。研究区MSVI、DVI分布状况见图1a、b，其中MSVI能够很好地去除土壤背景对光谱辐射响应的影响(文军等，1997)。DVI为红波段和近红外波段之差，对于土壤背景变化敏感(郭铌，2003)，能够较好地识别植被和水体。通过综合分析2类植被指数的分布状况，能够有效去除土壤、水体等非植被因素的影响。研究区内ADBH和FCC分布状态见图1c、d，其中平均胸径较大的林分主要分布在研究区的中南部，而平均胸径较小的林分则主要分布在研究区的中部及中北部。吴建强等(2015)研究表明，林木胸径分布(林木个体大小数量按径级的分布)能够反映林分生长状况、林木之间的竞争关系和林分密度状况。郁闭度较高的林分主要分布在研究区的中北部，西南部郁闭度较低，主要是因为人为活动的干扰频繁，导致森林受到较大影响。

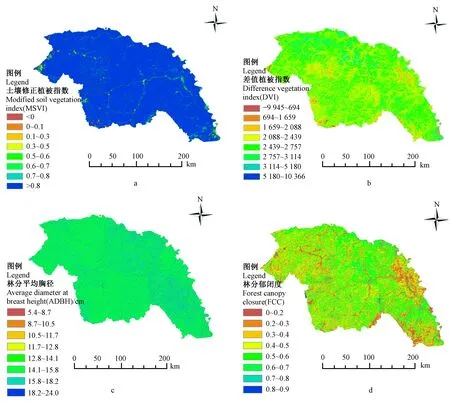
图1 预测变量空间分布Fig.1 Distributions of predictive variables

3.2 模型拟合及系数

地理加权回归模型与全局线性回归模型的因变量地位级指数都由MSVI、DVI、ADBH、FCC 4个指数来拟合，模型的拟合统计量见表5。

表5 模型的拟合统计量Tab.5 Fitting statistics of the models

3.2.1 全局模型系数分析表6所示为全局模型的回归系数。模型系数在显著性水平α=0.05下，所选4个变量均表现出较强的统计显著性，4个变量VIF值都远小于10，表明所选变量之间不存在多重共线性。

模型形式如下：

Y=-3.582+4.467x1+2.886x2+

0.272x3+0.002x4。

(19)

式中：Y为地位级指数；x1为MSVI；x2为ADBH；x3为FCC；x4为DVI。

表6 全局模型回归系数Tab.6 Model coefficient estimates of the global model

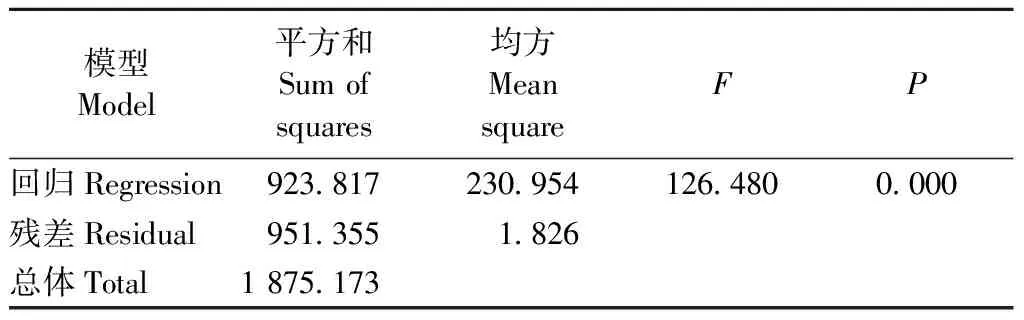
表7 全局模型方差分析Tab.7 Variance analysis of the global model

从模型系数来看，MSVI、DVI、ADBH和FCC的估计值均为正，说明这些变量与地位级指数呈正相关，其中MSVI的估计值最大且为正值，表明森林立地质量与遥感因子之间存在显著关系。其原因为MSVI是由近红外波段和红外波段运算得到的，其中波段3主要是叶绿素吸收波段，而波段4对绿色植被差异最为敏感。植被叶绿素含量与森林的生长和植被的光谱特征密切相关(杜华强等， 2009)，遥感植被指数与立地指数有着显著的相关关系，且MSVI的相关性略高于NDVI(马明东等， 2006)。

以上讨论均是针对于全局模型系数而言的，但全局模型建立在整个研究区之上，忽略了研究区内不同的森林条件和地形地貌，从而掩盖了变量间关系的局部特性，因此无法探究数据的空间关系。

3.2.2 GWR模型系数的空间分布 GWR模型能够在每一地理坐标处给出一个模型，即每个样地点都有一套模型参数。表8给出了GWR模型系数的几种统计量。

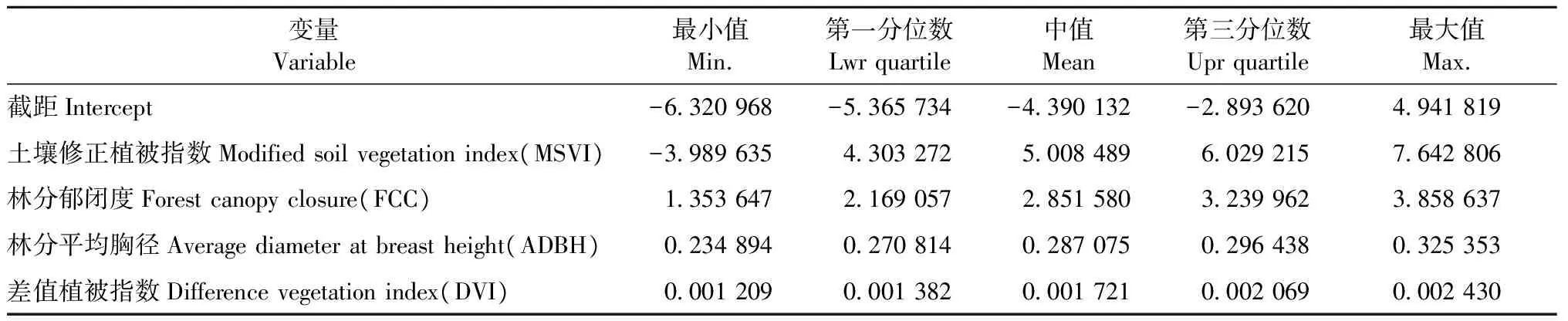
表8 地理加权回归模型系数估计值Tab.8 Model coefficient estimates of the GWR model

不难发现，多元线性回归模型系数与地理加权回归模型系数的中值最为接近，所选4个变量在全局模型和局域模型中对森林地位级指数均为正影响，如MSVI估计值除最小值外，其他数值在局域模型中均为正，表明虽然局域模型系数会随地理位置变化而变动，但是其对森林地位级指数的影响趋势与全局模型基本相同。地理加权回归模型能够对每一变量在所有样点上给出参数估计值，利用反距离法(inverse distance weighted，IDW)对模型中各变量对应参数分别插值得到GWR模型各个变量对应参数的空间分布结果。图2为GWR模型在预测森林地位级指数时各变量对应参数的空间分布。从图2a可以看出，除东部区域一部分外，其余大部回归系数均为正值，且回归系数呈现由中部向双侧递减的趋势，表明土壤修正植被指数在研究区中部对地位级指数具有最强影响力。综合整个研究区来看，土壤修正植被指数对地位级指数的影响均为正，说明保持其他条件不变时，较高MSVI处具有较高的地位级指数。在图2b中，中部区域回归系数较低，向两侧系数逐渐增加，表明两侧区域地位级指数对于差值植被指数的敏感度高于中部区域。从全图来看，差值植被指数对地位级指数的影响也是正向的。在图2c中，ADBH系数总体呈现东南部和西部较高，向中部逐渐减小，说明ADBH在中部对森林立地地位级指数的影响要低于其他地区。ADBH回归系数均为正值，说明林分平均胸径对地位级指数具有正向作用，在保持其他条件不变时，林分平均胸径的增加会导致地位级指数变大，且在研究区东南部和西部具有最强影响。图2d给出了林分郁闭度回归系数的空间分布，回归系数由研究区域两侧向中心地区逐渐递减，最小值出现在研究区中部且均为正值，说明林分郁闭度和森林立地地位级指数之间呈正相关关系，对地位级指数具有正影响，表明郁闭度较高的林分具有较高的地位级指数。

图2 GWR模型各变量对应参数的空间分布Fig.2 Distributions of variable parameters in GWR models

3.3 模型残差的空间自相关性分析

本研究通过计算全局模型和局域模型的全局Moran I并进行了基于随机假设的标准正态检验来评价2类模型残差的空间自相关性。国家森林资源一类清查样地的布设间隔为8 km，因此以8 km带宽计算了2类模型的全局Moran I以及基于基本假设的标准正态检验结果(Z值)，见表9。由表9可知，对于全局模型，标准正态检验Z值为7.54，远大于1.96，即拒绝随机假设，模型残差在空间中的分布并非完全随机；而GWR模型的Z值为-0.16，大于-1.96且小于1.96，说明GWR模型能够有效地消除模型的空间自相关性。

表9 全局模型和GWR模型残差全局Moran I及检验结果Tab.9 Global Moran I and test of the model residuals of the global model and GWR model

为了更好地比较全局模型和局域模型残差的空间关系，以8 km为间隔绘制了2类模型的残差空间相关图(图3)。由图3可知，GWR模型的空间自相关性在每一尺度上均小于全局模型。全局模型的空间自相关性随着距离的增加而减小，在一定距离(60 km)后，Moran I值稳定在0.03附近，意味着空间自相关性在这一步长范围内变小。GWR模型在整个研究区内Moran I均小于全局模型并且稳定在0附近，说明地理加权回归模型残差的空间自相关性很低乃至消失。地理加权回归模型因为考虑到了明确的空间位置关系和局域变量间的关系，成功降低了模型的空间自相关性。

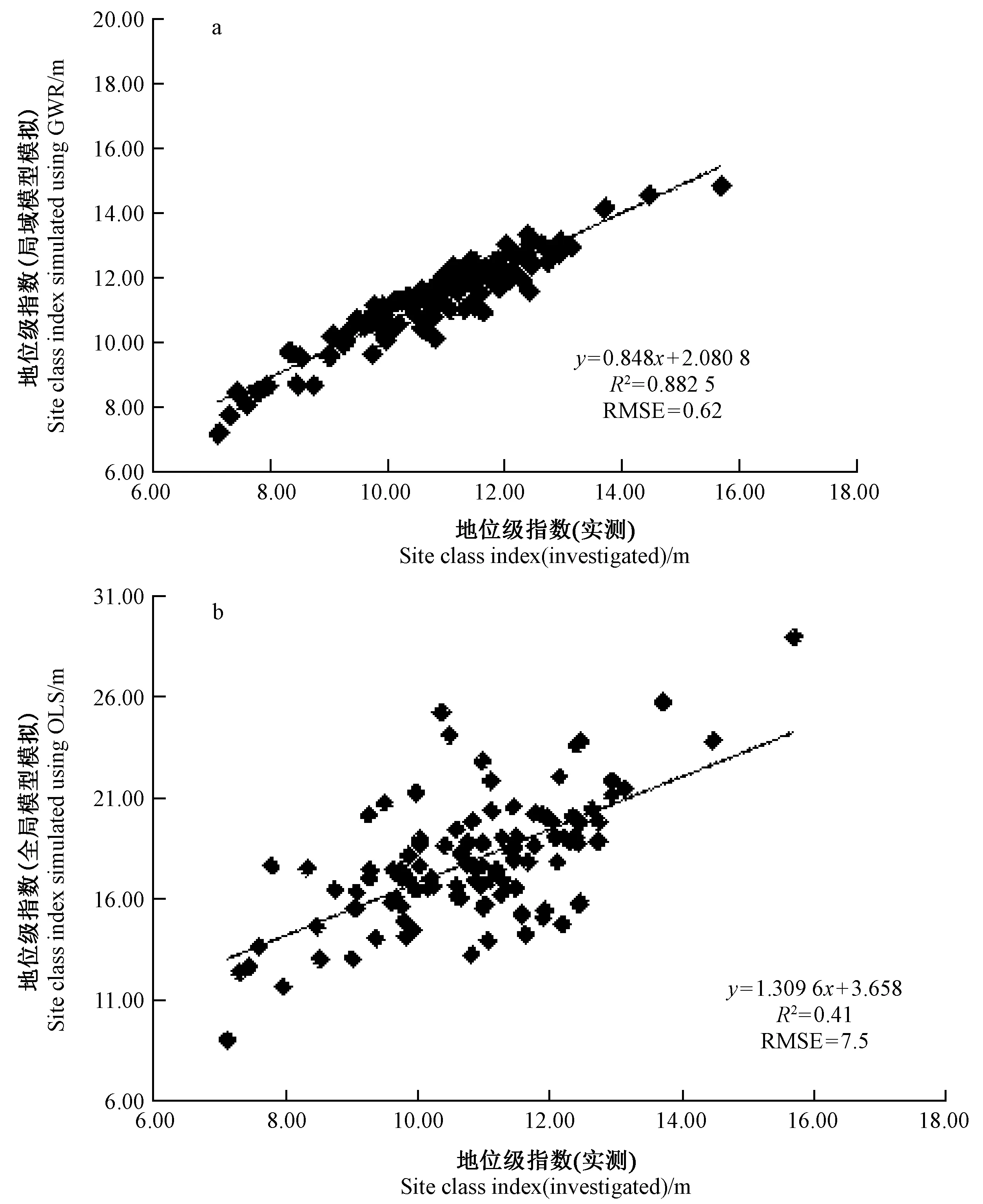
图4 局域模型和全局模型拟合结果精度分析Fig.4 GWR and OLS fitting result accuracy analysis

图3 地理加权回归模型和全局模型的残差空间相关Fig.3 Correlogram of Moran I of the model residuals of the global and GWR models

3.4 模型精度验证结果

局域模型和全局模型SCI模拟结果和实测结果的相关关系分别如图4a、b所示，局域模型的观测值与预测值R2和RMSE分别为0.88和0.62，而全局模型的实测值与拟合值的R2和RMSE分别为0.41和7.5，因此，GWR模型在SCI估计上具有更高的精度。3.5 森林地位级指数拟合结果

与全局模型相比，因GWR模型具有拟合精度更高、验证精度更高、误差更小、产生残差更理想等优点，因此选择GWR模型对研究区森林地位级指数进行定量分析，并绘制研究区森林地位级指数的空间分布图，如图5所示。

图5 研究区林地地位级指数分布Fig.5 Site class index distribution of study area

由图5可知，大兴安岭地区森林地位级指数的变化范围为0～28 m，分布在8～17 m范围内最多，与现地调查结果相符。研究区北部地位级指数高于南部，呈北高南低的分布趋势，北部和西北部较高地位级指数有明显聚集现象，其中最大值出现在研究区最北端。南部地位级指数主要分布在3～10 m范围，地位级指数较低。主要原因为南部人类活动较为频繁，对自然环境破坏较为严重，而北部人类活动则相对较少。综合分析研究区数字高程模型图和地位级指数分布图(图6)可知，研究区东部和北部海拔较低，地形起伏变化较小(0～600 m)，具有较高地位级指数，而中部、南部海拔较高，地形起伏变化较大(600～1 500 m)，地位级指数较小。这是因为随着海拔增加，土壤厚度降低，水土更易流失且地表温度下降，影响了植被的生长和发育，也就是立地质量较低的原因(保娅等， 2014)。

图6 研究区域高程分布Fig.6 Elevation distribution of study area

4 讨论

本研究通过建立全局多元线性回归模型和局域地理加权回归模型研究黑龙江省大兴安岭地区森林地位级指数，取得了较好的估算效果。通过比较发现，局域模型的拟合效果和精度明显高于全局模型。通过分析2类模型残差的空间自相关性发现，地理加权回归模型在很大程度上能够有效消除残差的空间自相关性。这是因为地理加权回归模型在模型拟合时加入了样地的位置信息，并且通过距离衰减函数来进行加权，在每个样地都有一套独立的预测模型，残差的空间自相关性更不明显，也更加符合传统统计模型中关于残差间相互独立的基本假设，使得建模过程更加科学合理，这与前人的研究相符合。

同时需要指出的是，对地位级指数估算模型影响较大的是地面数据和遥感数据的质量，如林分平均高和林分平均年龄的准确估计。在林业资源调查中，林分平均高与林分平均年龄的测量主要依靠人工主动获取，难免产生误差对估算精度造成影响。其次，研究所采用的非同一时相遥感图像也会对模型产生影响，鉴于研究区较大，同一时相遥感图像获取困难，因此本研究采用的是植被生长季(6—9月)期间遥感图像，认为在大区域尺度下植被生长季期间遥感光谱信息变化可以忽略。另外，在研究中可以考虑加入其他遥感数据对各个变量进行拟合。

5 结论

大兴安岭地区地位级指数分布范围为0～28 m，且在8～17 m范围内分布最为广泛，呈东高西低、北高南低的分布趋势。

成功建立了遥感因子和森林地位级指数之间的关系。就模型而言，在影响森林立地质量的4个变量中，土壤修正植被指数影响最为显著，在很大程度上可以反映立地质量。

本研究通过遥感因子与林分因子的结合完成了黑龙江省大兴安岭地区森林立地质量的评价，能够大面积快速有效地估测森林立地条件，这是研究森林生态系统的结构与功能、了解森林生态系统生产力、确定合理的经营管理方案的重要基础。

保娅，达哇卓玛. 2014. 不同海拔高度温、湿度对土壤养分的影响. 青海草业，23(4)：16-18.

(Bao Y，Daw Z.2014. Effects of temperature and humidity on soil nutrients at different altitudes. Qinghai Prataculture，23(4)：16-18.[in Chinese])

杜华强，葛宏立，范文义，等. 2009. 马尾松针叶光谱特征与其叶绿素含量间关系研究. 光谱学与光谱分析，29(11)：3033-3037.

(Du H Q，Ge H L，Fan W Y，etal.2009.Study on relationships between total chlorophyll with hyperspectral features for leaves ofPinusmassonianaforest. Spectorscopy and Spectral Analysis，29(11)：3033-3037. [in Chinese])

巩垠熙，何诚，闫飞，等. 2013. 人工神经网络结合多光谱遥感数据用于立地质量评价.光谱学与光谱分析， 33(10)：2815-2822.

(Gong Y X，He C，Yan F，etal.2013. Study on artificial neural network combined with multispectral remote sensing imagery for forest site evaluation. Spectorscopy and Spectral Analysis，33(10)：2815-2822. [in Chinese])

郭铌. 2003. 植被指数及其研究进展. 干旱气象，(4)：71-75.

(Guo N.2003. Vegetation index and its research progress. Arid Meteorology，(4)：71-75. [in Chinese])

康冰，刘世荣，蔡道雄，等. 2009. 马尾松人工林林分密度对林下植被及土壤性质的影响. 应用生态学报，20(10)：2323-2331.

(Kang B，Liu S R，Cai D X，etal. 2009. Effects ofPinusmassonianaplantation stand density on understory vegetation and soil properties. Chinese Journal of Applied Ecology，20(10):2323-2331. [in Chinese])

李龙，姚云峰，秦富仓，等. 2016. 基于地理加权回归模型的土壤有机碳密度影响因子分析. 科技导报，34(2):247-254.

(Li L，Yao Y F，Qin F C，etal. 2016. Analysis on influence factors of soil organic carbon density using a geographically weighted regression model. Science & Technology Review，34(2): 247-254. [in Chinese])

刘畅. 2014. 黑龙江省森林碳储量空间分布研究. 哈尔滨：东北林业大学博士学位论文.

(Liu C.2014.Spatial distribution of forestry carbon storage in Heilongjiang Province. Harbin：PhD thesis of Northeast Forestry University. [in Chinese])

刘畅，李凤日，甄贞. 2014. 空间误差模型在黑龙江省森林碳储量空间分布的应用. 应用生态学报，25(10)：2779-2786.

(Liu C，Li F R，Zhen Z. 2014. Prediction of spatial distribution of forest carbon storage in Heilongjiang Province using spatial error model. Chinese Journal of Applied Ecology， 25(10): 2779-2786. [in Chinese])

刘正显. 2015. 基于GWR模型的凉水自然保护区森林生物量空间分布研究. 哈尔滨：东北林业大学硕士学位论文.

(Liu Z X.2015.Research on the spatial distribution of Liangshui Nature Reserve biomass based on geographically weighted regression. Harbin：MS thesis of Northeast Forestry University. [in Chinese])

骆期邦，吴志德，肖永林. 1989. 立地质量的树种代换评价研究. 林业科学，25(5):410-419.

(Luo Q B，Wu Z D，Xiao Y L.1989. Study on the species substitution site quality assessment. Scientia Silvae Sicinae，25(5):410-419. [in Chinese])

马建路. 1993. 天然红松林立地类型划分与立地质量评价的研究. 哈尔滨：东北林业大学硕士学位论文.

(Ma J L.1993. Study on classification and evaluation of site quality with natural Korean pine. Harbin：MS thesis of Northeast Forestry University. [in Chinese])

马明东，江洪，刘世荣，等. 2006. 森林生态系统立地指数的遥感分析. 生态学报，26(9):2810-2816.

(Ma M D，Jiang H，Liu S R，etal.2006.The preliminary analysis of forest ecosystem site index using remote sensed data. Acta Ecologica Sinica，26(9):2810-2816. [in Chinese])

覃文忠. 2007. 地理加权回归基本理论与应用研究. 上海：同济大学博士学位论文.

(Qin W Z.2007.The basic theoretics and application research on geographically weighted regression. Shanghai：PhD thesis of Tongji University.[in Chinese])

宋喜芳，李建平，胡希远. 2009. 模型选择信息量准则AIC及其在方差分析中的应用. 西北农林科技大学学报:自然科学版，37(2): 88-92.

(Song X F，Li J P，Hu X Y.2009.Model selection criterion AIC and its application in ANOVA. Journal of Northwest A&F University:Natural Sciences Edition, 37(2): 88-92. [in Chinese])

王鹤智. 2012. 东北林区林分生长动态模拟系统的研究.哈尔滨：东北林业大学博士学位论文.

(Wang H Z. 2012.Dynamic simulating system for stand growth of forests in north China. Harbin：PhD thesis of Northeast Forestry University. [in Chinese])

文军，王介民. 1997. 一种由卫星遥感资料获得的修正的土壤调整植被指数. 气候与环境研究，2(3):105-112.

(Wen J，Wang J M.1997. A modified soil adjusted vegetation index obtained from satellite remote sensing data. Research on Climate and Environment，2 (3):105-112. [in Chinese])

吴建强，王懿祥，杨一，等. 2015. 干扰树间伐对杉木人工林林分生长和林分结构的影响. 应用生态学报， 26(2)：340-348.

(Wu J Q，Wang Y X，Yang Y，etal. 2015. Effects of crop tree release on stand growth and stand structure ofCunninghamialanceolataplantation. Chinese Journal of Applied Ecology，26(2):340-348. [in Chinese])

相聪伟. 2010. 杉木人工林立地指数方程的研究. 北京：中国林业科学研究院硕士学位论文.

(Xiang C W.2010.Study on site index equation ofCunninghamialanceolataplantations. Beijing：MS thesis of Chinese Academy of Forestry. [in Chinese])

肖兴威. 2004. 影响亚热带东部森林结构的因子分析.东北林业大学学报，32(5):19-20.

(Xiao X W. 2004. Analysis on factors influencing the structure of forests in the east subtropical zone. Journal of Northeast Forestry University，32(5):19-20. [in Chinese])

Brunsdon C，Charlton M. 1998. Geographically weighted regression-modelling spatial non-stationarity. Journal of the Royal Statistical Society，47(2):431-443.

Carmean W H. 1978. Site index curves for northern hardwoods in northern Wisconsin and Upper Michigan. USDA Forest Service Research Paper NC (USA)，160.

Curt T，Bouchaud M，Agrech G. 2001. Predicting site index of Douglas-Fir plantations from ecological variables in the Massif Central area of France. Forest Ecology & Management，149(1/3):61-74.

Louw J H，Scholes M.2002. Forest site classification and evaluation: a South African perspective. Forest Ecology & Management，171(1/2):153-168.

Skovsgaard J P，Vanclay J K. 2008. Forest site productivity: a review of the evolution of dendrometric concepts for even-aged stands.Forestry，81(1):13-31.

Zhang L，Shi H. 2004. Local modeling of tree growth by geographically weighted regression.Forest Science，50(2):225-244.

Zhen Z，Li F，Liu Z，etal. 2013. Geographically local modeling of occurrence，count，and volume of downwood in northeast China. Applied Geography， 37(4):114-126.

(责任编辑石红青)

Remote Sensing Analysis of Forest Site Quality in Daxing’an Mountain Based on GWR

Li Mingze Guo Hongjun Fan Wenyi Zhen Zhen

(CollegeofForestry,NortheastForestryUniversityHarbin150040)