基于多变量分析的环肋圆柱壳结构特性研究

梁来雨，汪志强

（武汉第二船舶设计研究所，湖北 武汉 430205）

基于多变量分析的环肋圆柱壳结构特性研究

梁来雨，汪志强

（武汉第二船舶设计研究所，湖北 武汉 430205）

为了从整个可行解空间研究圆柱壳结构特性，采用全因子试验设计获得变量范围内的可行解空间，通过相关理论推导计算得到不同结构形式圆柱壳的强度、稳定性以及振动频率等指标。采用相关性分析、主成分分析以及变量聚类分析方法根据可行解空间的数据对环肋圆柱壳强度、稳定性、振动频率之间以及这些属性与设计变量之间的关系进行研究。采用相关系数矩阵图、主成分分布图以及谱系聚类图将多变量分析的结果可视化。对可视化结果进行分析发现了圆柱壳结构属性之间的矛盾性，变量、属性之间的相似性和关系的复杂性。通过多变量分析得到的相关结论能够作为实际工程设计的参考。

环肋圆柱壳；结构特性；多变量分析；相关分析

加筋圆柱壳以其良好的承压性能被广泛应用于水下结构，潜艇主体采用环肋圆柱壳结构。设计规范[1]采用的是校核的方法，结构相关应力和临界载荷的值满足校核条件，即认为设计满足要求。在实际设计中为了使强度、稳定性指标之间更均衡，需要对设计变量与属性之间的关系进行分析，通过各变量与属性之间的关系，来调整结构形式让结构更合理。

目前更多的是对圆柱壳结构变量对属性的影响进行分析，采用“控制变量”方法，通过改变某个变量来分析结果的变化。如：黄振熙等[2]采用参数化方法研究潜艇耐压液舱的优化设计，分析了纵骨间距、肋距变化对液舱重量的影响。在纵骨间距不变的情况下研究了板厚、型材等变量对肋骨间的影响。M.Bagheri等[3]在圆柱壳的优化中，研究了加肋对结构重量的影响以及肋骨分布情况对结构频率和临界载荷的影响。

实际上，圆柱壳结构变量之间存在复杂的耦合关系，一个变量变化可能引起其它变量的改变。“控制变量”难以考虑变量之间的耦合情况。为更深入地认识圆柱壳设计变量之间、属性之间以及设计变量与属性之间的内在关系。本文从多变量分析的角度出发，研究圆柱壳设计变量、属性之间的相互关系。采用多变量分析方法从可行解空间对圆柱壳结构特性进行分析，采用全因子试验设计[4]得到可行解空间。用相关性分析[5]、主成分分析[6]以及变量聚类[7]等方法根据试验数据对圆柱壳结构变量、属性之间的相互关系进行分析，并将多变量分析的结果可视化。对变量、属性进行相关性分析，发现了属性之间的矛盾性以及变量与属性之间关系的复杂性，主成分分析和变量聚类的结果显示了变量、属性之间存在的相似性。

1 理论分析

1.1 强度、稳定性和振动分析

潜艇典型舱段及其受力如图1所示。L为舱段长度；l为肋骨间距；h为壳板厚度；R为圆柱壳中面半径；e为肋骨对壳中面偏心距，圆柱壳的两端刚性支撑，外加均匀外压力p。

图1 典型舱段以及受力示意图

需做强度校核的应力有[1]：支座处壳横剖面的内表面应力σ'1，跨中壳纵剖面的中面应力σ02以及肋骨的应力σl，计算式为[8]：

式中：p为计算深度处的静水压力，系数K1，K02，Kl以及其它辅助函数详见文献[5]。

静水压力下，当圆柱壳肋骨的刚度超过其临界刚度时，首先是肋骨之间的壳板失稳。壳板局部失稳的理论临界载荷计算式为[8]：

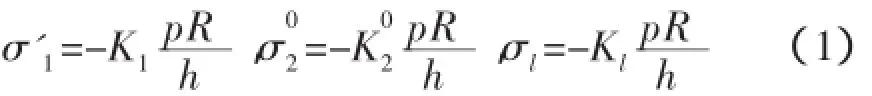
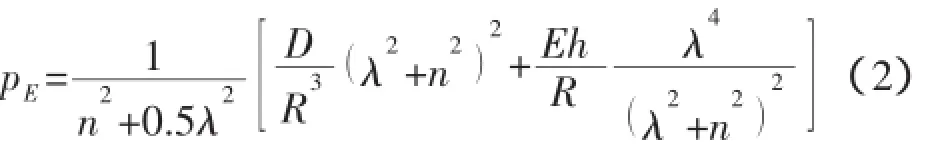
式中：λ=πR/l，D=Eh3/2/(1-μ2)，n为失稳时圆周上的整波数。

整体失稳的理论临界载荷计算式为：

式中：m为失稳时轴线方向的半波数，I为计及带板的肋骨惯性矩，λ'=πR/L。

对上述计算的理论临界值进行修正。

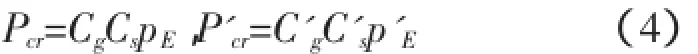
式中：Cg，C'g分别为圆柱壳局部板壳失稳和整体失稳时的几何非线性修正系数，Cs，C's分别为圆柱壳局部板壳失稳和整体失稳时材料物理非线性修正系数。计算过程中需要使用设计图谱，采用一维3次样条插值法进行求解。

圆柱壳重量为：

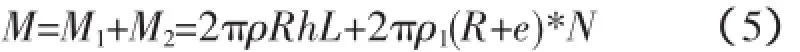
式中：M1为圆柱壳重量；M2为肋骨的重量；ρ为壳板材料密度；ρ1为肋骨单位长度的重量；N为肋骨数量，肋骨为外肋布置；R+e为肋骨的中性轴半径。

环肋圆柱壳在静水压力下自由振动频率的求解问题，最终可转化为关于频率的3次代数方程[9]。

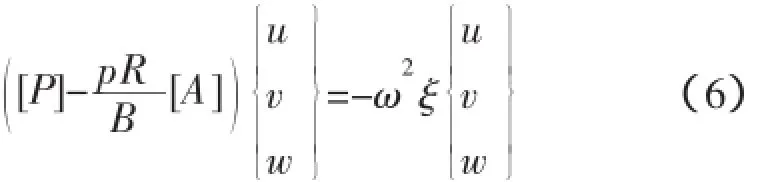
式中：ξ=ρhR2/B，B=Eh/(1-μ2)，这里采用“均摊法”将肋骨的作用均摊到壳板厚度上，为板壳的相当厚度。ω为圆频率，f=ω/2/π。u，v，w分别为壳体在轴向、轴向和径向的位移。矩阵[A]、[P]的元素详见文献[9]。方程（6）有三个特征值，在这里只需求其中最小的特征值对应的圆柱壳的自由振动频率f，就能够满足工程上的需要。

1.2 多变量分析

圆柱壳结构含有强度、稳定性重量等多个属性以及舱段长度、半径、板厚等多个变量，要了解多个变量之间的关系，可以用多变量分析方法。

为了更全面地了解圆柱壳结构的特性，本文对给定的设计变量进行全因子试验设计。全因子试验设计指全部因子的所有水平的所有组合都至少进行一次试验[4]。圆柱壳结构设计为离散变量问题，给定了变量的范围及水平用全因子试验设计能得到所有可行解。本文圆柱壳结构各变量为：壳板厚度h按标准[10]选取，肋距l按0.05 m的倍数递增，肋骨型号cn按标准[11]选取。实际建造中，圆柱壳半径R和舱段长度L都采用整型规格。

相关系数是衡量两个变量之间不确定相关性常用的方法。最常用的相关系数是英国的统计学家Karl Pearson提出的简单相关系数，两个变量X，Y之间的相关系数定义为[5]：

式中：Cov(X,Y)为两个变量的协方差，Var(X)、Var(Y)分别为两个变量的方差。

对于多个变量，通过计算各变量之间的相关系数可得到相关系数矩阵。Taiyun Wei[12]提出了一系列将相关系数矩阵可视化的方法，其中有一种是定量与定性相结合的方法，将表示相关系数的圆放在矩阵的下三角部分，通过圆的大小表示相关性的大小，用圆的颜色表示相关性的正负，将相关系数放在上三角部分，称之为相关系数图。

主成分分析是一种多变量分析方法，利用降维的思想将原来的多个变量转化为少数的几个主成分，通过原变量与主成分之间的关系得到原变量在主成分空间的分布情况，根据各变量在主成分空间的相对位置来分析各变量之间的关系[5]。

主成分分析的一般步骤：（1）构造初始矩阵，并对数据标准化处理；（2）计算相关系数矩阵及其特征值；（3）根据特征值计算主成分的方差贡献率；（4）计算主成分与原变量之间的因子负荷量。根据主成分与原变量之间的因子负荷量就能够得到原变量在主成分空间的分布[6]。

聚类分析是研究对指标或者样本进行分类的一种多元统计方法。对变量聚类称为R型聚类，变量聚类按照变量之间的相似性对变量进行分类，使同类中变量之间的相似性较大，不同类变量间的差异性较大。通常用相似系数或者是相关系数来衡量变量之间的相似性[7]。层次聚类的结果常用谱系聚类图表示[6]，通过谱系图能直观地看出各变量之间的聚类关系。

2 算例及讨论

以某典型舱段为例。材料参数：E=1.96×105MPa，泊松比μ=0.3，屈服极限σs=590 MPa。设计变量的取值范围如表1所示。

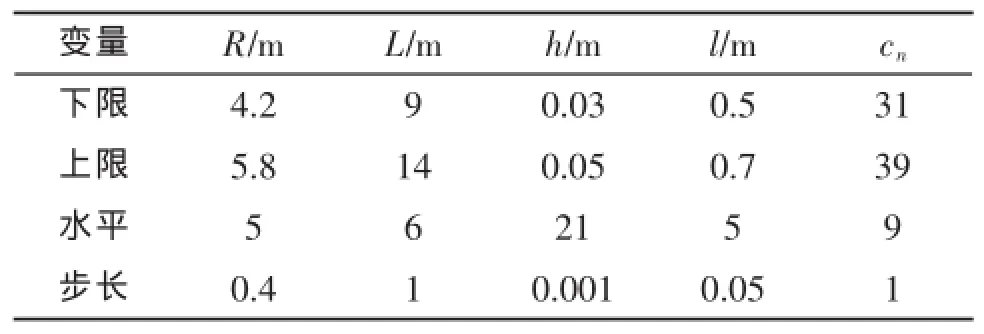
表1 典型舱段圆柱壳设计变量取值范围

按照规范的校核条件，3个应力和2个临界载荷的约束范围：

此外，为了解圆柱壳结构的振动特性与强度、稳定性特性之间的关系，对圆柱壳结构的自由振动频率进行考虑，也对其进行约束：

根据表1以及约束条件式（8）～式（9），利用全因子试验设计得到2 081个试验样本。每个样本都有5个设计变量和7个不同的属性，构成2 081×12的数据矩阵。

利用式（7）根据试验数据计算变量、属性之间的相关系数，相关系数图如图2所示。

图2 属性、变量之间的相关系数图

从图2可看出，3个应力之间具有较大的正相关性（0.59，0.85，0.9）。2个临界载荷之间正相关但相关不大（0.3）。3个应力与2个临界载荷之间都是负相关（-0.22～-0.92），说明强度与稳定性之间的矛盾性。重量与肋距之间负相关（-0.27）与其它变量之间都是正相关，增加肋距有助于减轻结构重量。频率与重量和舱段长度之间有显著的负相关性（-0.69，-0.91），说明频率越低对应结构的重量越重、舱段长度越长。与其它变量与属性之间的相关性相比，板厚与3个应力及局部临界载荷之间都有显著的相关性（-0.54～-0.89,0.8）之间，说明板厚是一个比较重要的变量，设计中应重点关注。肋骨应力与肋骨型号的相关性并不大（-0.1），与半径、肋距以及板厚有一定的相关性（-0.4，-0.54）。

图2设计变量之间相关性能够显示圆柱壳结构形式的特性。如：肋距与板厚之间正相关（0.45）、与半径负相关（-0.41），半径与肋骨型号正相关（0.49），肋距大则板厚越厚、半径越小，半径越小则肋骨型号越小，说明变量之间是相互关联性较大。这些变量与各属性之间的相关性又不相同，如：肋距越大、肋骨型号小、半径小则结构重量越小，而壳板越厚则重量可能越重；肋距大、壳板厚，局部稳定性好；肋骨型号小，则整体稳定性不好。说明变量、属性之间关系的复杂性和矛盾性。体现了圆柱壳结构设计中多属性、多变量之间协调、均衡的复杂程度高，设计难度大。

为了进一步了解圆柱壳的结构特性，对试验数据进行主成分分析。特征值以及对应的方差贡献率如表2所示。

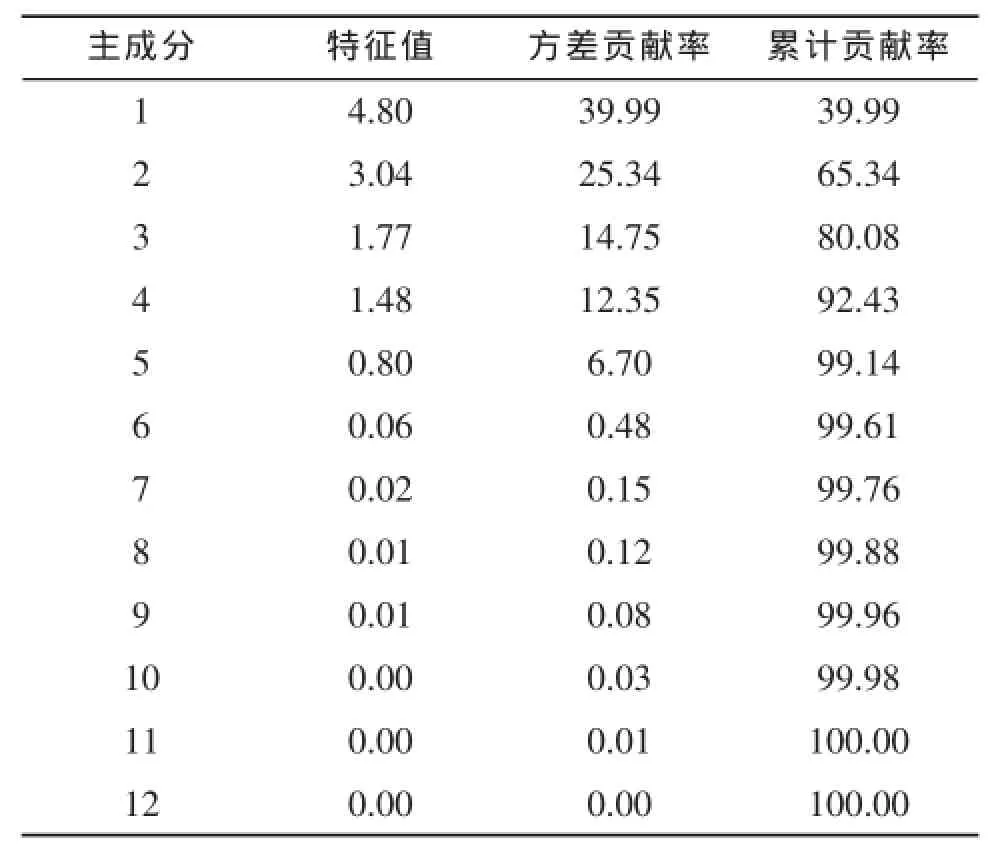
表2 特征值和方差贡献率

根据表2，前4个主成分的累计贡献率达到92.43%，取4个主成分就足够表达原变量的大部分信息。主成分与原变量之间的载荷矩阵如表3所示。

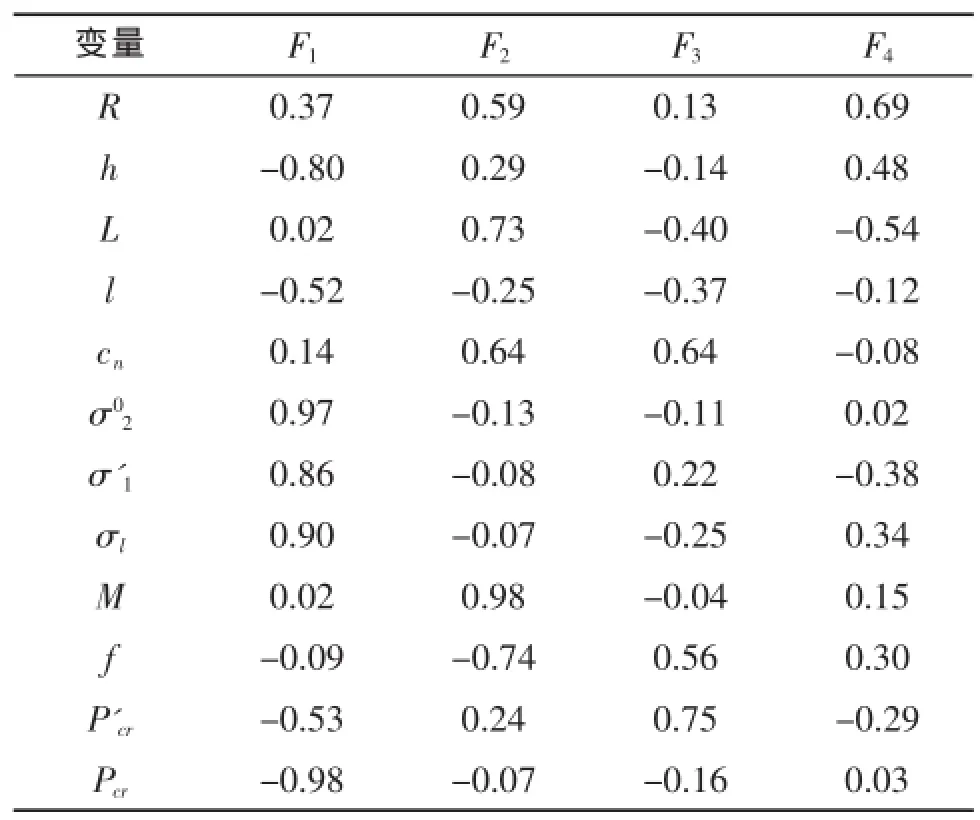
表3 主成分矩阵

表3中F1～F4代表的是前4个主成分。根据主成分矩阵，可得到原变量在主成分空间的分布。为了便于观察这里分别取前3个和前2个主成分，得到原变量随前3个和前2个主成分的分布如图3（a）、（b）所示。

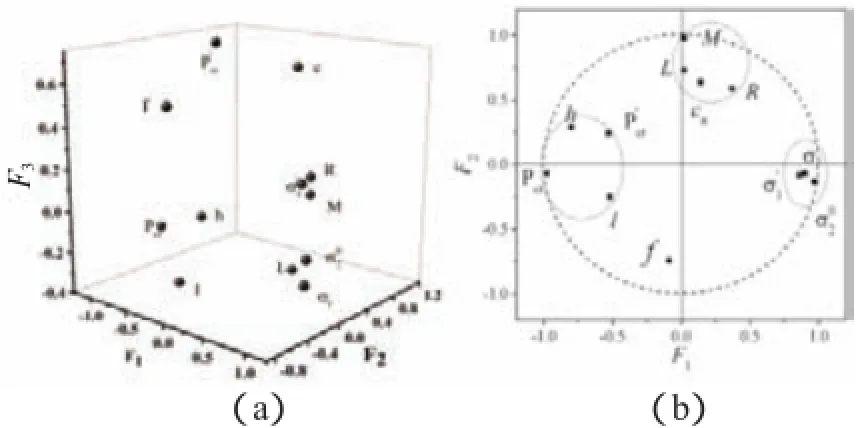
图3 主成分分布图

根据图3（a），在3个主成分空间内：M与R，L之间距离较近。P'cr和cn之间相距较近。3个应力之间距离较近。Pcr与h，l之间较近。f单独在一边与其它变量都相距较远。

图3（b）在第1和第2主成分平面内：3个应力之间相距很近，M与L，cn和R之间相距较近，两个临界载荷与h，l分布在同一个区域，频率单独在一边。

变量随不同数目主成分的分布并不完全一致。分析表3，cn和P'cr都与第3个主成分有较大的相关性，说明两个主成分并不足以反映原变量之间的原始关系。根据表2，两个主成分只包含了原变量的65.34%的信息，3个主成分包含了原变量的80.08%的信息。相对于两个主成分，3个主成分包含原变量的信息更多，原变量随3个主成分的分布与它们实际的关系更接近，但还是有部分信息损失。

对比图3和图2可看出，在主成分空间内，正相关且相关系数越大的变量之间的距离越近，如：3个应力之间，重量与R，L之间。负相关且相关系数绝对值越大的变量之间的距离越远，如：3个应力与局部临界载荷之间。可见主成分分布图通过原变量在主成分空间的相对位置反映了变量之间的聚类特性。

对变量聚类更常用的方法是层次聚类。采用变量之间的相关系数（如图2）表示变量之间的相似性，将变量聚类的结果用树状谱系图表示，如图4所示。

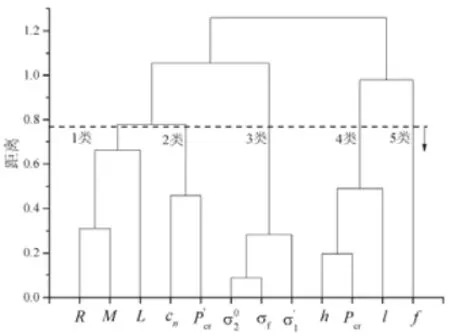
图4 变量聚类谱系图

按照给定的距离（图4中虚线所示）可将变量分为5类，从左到右5类分别为:M与R，L为第1类，P'cr和cn为第2类，3个应力为第3类，Pcr与h，l为第4类，频率单独为第5类。

根据图5：频率是一个很特别的属性，与其他属性和变量之间都没有太大的相似性；整体临界载荷与局部临界载荷之间的相似性不大，这与它们之间的相关系数不大相对应；结构重量与半径R、舱段长度L之间相似性最大，以最小重量为设计目标时，可以重点考虑这两个变量。P'cr与肋骨型号的关系密切，设计中适当选择较大型号的肋骨有助于提高结构的整体稳定性。

对比图4和图3，变量聚类结果与变量在3个主成分空间的分布情况是一致的。说明主成分分析中至少需要3个主成分才能将原变量之间原本关系表达清楚。可见由主成分分布图得到变量之间聚类特性的准确性与主成分包含原变量信息的多少有直接的关系，当所需主成分较多时，变量在主成分空间的分布情况较难获取。

变量聚类反映的是变量之间原本的关系，没有损失变量的信息，由变量聚类法得到的各变量之间的分类结果更可信。

3 结论

本文采用相关性分析、主成分分析以及变量聚类分析3种多变量分析方法利用可行解空间的数据对圆柱壳进行了结构特性分析，并将分析的结果可视化来直观地获取有用的信息。得到如下的结论：

（1）根据变量和属性之间的相关系数：圆柱壳的强度、稳定性以及重量属性之间是相互矛盾的；圆柱壳壳板厚度是一个较重要的变量，对各属性的影响都较大，在设计中应重点关注；频率与舱段长度以及重量都有较大的相关性，频率越低对应的舱段长度可能越长、结构重量也可能越重。

（2）3个主成分空间内：重量、半径、舱段长度之间距离较近。整体临界载荷和肋骨型号相距较近。3个应力相距较近。局部临界载荷与板厚、肋距之间较近。频率与其它变量之间都相距较远。

（3）在主成分空间内，正相关且相关系数越大的变量之间的距离越近，负相关的变量且相关系数绝对值越大的变量之间的距离越远，主成分分布图通过原变量在主成分空间的相对位置反映了变量之间的聚类特性。

（4）变量层次聚类的结果与3个主成分分布中变量的分布是相同的。相对于主成分分析的结果来说，变量聚类反映的是变量之间原本的关系，没有损失变量之间的原本信息，得到的变量分类结果更可信。

[1]中国船舶工业总公司.GJB/Z21A-2001潜艇结构设计计算方法[S].2001.

[2]黄振熙,王祖华.潜艇耐压液舱设计[J].舰船科学技术,2012,34(4):30-35.

[3]M Bagheri,A A Jafari,M Sadeghifar.Multi-objective optimization of ring stiffened cylindrical shells using a genetic algorithm[J]. Journal ofSound and Vibration,2011,330(3):374-384.

[4]闵亚能.实验设计（DOE）应用指南[M].北京:机械工业出版社,2011:80-90.

[5]WolfgangHärdle,Léopold Simar.Applied Multivariate Statistical Analysis[M].NewYork:Springer,2007:84-89.

[6]何晓群.多元统计分析[M].北京:中国人民大学出版社,2008:152-157.

[7]高惠璇.应用多元统计分析[M].北京:北京大学出版社,2004:259-261.

[8]许辑平,等.潜艇强度[M].北京:国防工业出版社,1980:5-30.

[9]中国科学院力学所.加筋圆柱曲板和圆柱壳[M].北京:科学出版社,1983:157-178.

[10]中国船舶工业总公司.GB/T3432-92.船用钢板尺寸和重量[S].1992.

[11]中国船舶工业总公司.CB/T3433-92.船用对称型钢尺寸、外形、重量及允许偏差[S].1993.

[12]TaiyunWei,ViliamSimko.VisualizationofaCorrelationMatrix[EB/OL].[2016-04-21].https://cran.r-project.org/web/packages/corrplot/.

Study on the Structural Characteristics of Ring-Stiffened Cylindrical Shell Using Multivariate Analysis

LIANG Lai-yu,WANG Zhi-qiang
Wuhan 2nd Ship Design&Research Institute,Wuhan 430205,Hubei Province,China

To analyze the structural characteristics of cylindrical shell in the feasible solution space,the full factorial experiment design method is applied to obtain the feasible solution space.Multivariate analysis approaches,such as correlation analysis,principal components analysis and cluster analysis,are used to study the structural characteristics of ring-stiffened cylindrical shell.The correlation coefficient matrix,principal component map and dendrogram of variable cluster are utilized to show the results of multivariate analysis.By analyzing the visual results,the incompatibility of attributes and the similarity and complicated relations among attributes and variables of cylindrical shell are found.The useful conclusions obtained from the multivariate analysis approaches can be used as reference in practical engineering design.

ring-stiffened cylindrical shell;structural characteristics;multivariate analysis;correlation analysis

U663

A

1003-2029（2017）03-0097-06

10.3969/j.issn.1003-2029.2017.03.018

2017-01-02

梁来雨（1986-），男，工程师，主要研究方向为船舶结构及救生。E-mail：465633580@qq.com