VMD和ICA联合降噪方法在轴承故障诊断中的应用

马增强， 柳晓云， 张俊甲， 王建东

(石家庄铁道大学 电气与电子工程学院，石家庄 050043)

VMD和ICA联合降噪方法在轴承故障诊断中的应用

马增强， 柳晓云， 张俊甲， 王建东

(石家庄铁道大学 电气与电子工程学院，石家庄 050043)

针对振动信号易受噪声干扰的影响、故障特征提取困难的问题，提出一种基于变分模态分解(Variational Mode Decomposition, VMD)和独立分量分析(Independent Component Analysis, ICA)相结合的去噪方法。该方法首先利用VMD算法将振动信号分解成若干不同频率的本征模态分量(Intrinsic Mode Function, IMF)，有效的抑制了LMD分解中存在的模态混叠现象和端点效应等问题，然后依据峭度准则选取相应分量进行重构，引入虚拟噪声通道；最后利用FastICA将重构后信号再次进行去噪处理，分离出有效的故障特征分量，从而识别故障类型。将该方法应用到滚动轴承故障数据中，并与LMD-ICA方法作对比，结果表明，提出方法不仅能够有效的解决去噪过程中丢失故障信息以及由于模态混叠导致噪声不能完全去除的问题，还能更清晰、准确地提取出故障特征频率。

变分模态分解；独立分量分析；降噪；滚动轴承；故障诊断

滚动轴承是旋转机械中不可或缺的部件之一，据统计，在旋转机械中，约有30% 的机械故障由滚动轴承引起，滚动轴承质量的好坏对机械设备工作状况有很大影响。因此，对滚动轴承的故障诊断具有重要的意义。

机械系统中，由于受复杂背景噪声以及其它干扰源影响，导致故障特征难以精确地提取出来。一些学者在振动信号降噪方面做了大量研究。Wu等[1]提出了经验模态分解(Empirical Mode Decomposition，EMD)算法，这是目前广泛使用的一种自适应信号处理方法，把非平稳信号分解成不同频段的模态分量进而转化成平稳信号进行分析。苏文胜等[2]将EMD应用到滚动轴承早期故障诊断中，实现了轴承故障诊断。吴小涛等[3]针对 EMD 的模态混叠，用集成经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)清晰地提取到故障特征信息，该方法可自适应地实现非平稳振动信号降噪。

Lin[4]提出了局部均值分解(Local Mean Decomposition，LMD)。陈亚农等[5]将LMD算法应用到滚动轴承故障诊断中，并提取出故障特征频率。鞠萍华等[6]通过LMD得到若干个PR(Production Functions)分量，并对每一个分量进行能量算子解调，从而进行故障诊断，并指出了该方法优于EEMD诊断方法。

EEMD或者LMD被广泛地应用在故障特征提取方面，然而两者都属于递归“筛选”模态，存在端点效应和模态混叠现象，且受采样频率影响，分解误差较大。文献[7]提出一种自适应信号处理新方法-变分模态分解(Variational Mode Decomposition，VMD)，该方法通过迭代搜寻变分模型最优解从而确定每个分解分量的频率中心和带宽，可以自适应地实现信号的频域剖分和各分量的有效分离。相比EEMD和LMD的递归“筛选”模态，VMD将信号分解转化为非递归、变分模态分解模态，表现出更好的噪声鲁棒性。

独立分量分析(Independent Component Analysis, ICA)是一种基于样本高阶统计信息的新的信号处理方法[8-10]，目前已广泛应用在通信信号处理、语音信号降噪等各个领域。为了进一步提高降噪效果，在以上研究的基础上，本文提出一种基于VMD与ICA联合降噪的方法，并将该方法应用在滚动轴承的故障诊断中。通过对实测数据分析结果表明，本文提出方法能够有效地实现特征信号提取，相比其他方法降噪效果更好。

1 VMD-ICA联合降噪方法基本原理

1.1 变分模态分解原理

VMD是一种新的信号分解估计方法，是基于经典维纳滤波、希尔伯特变换和混频的变分问题求解过程，该方法通过迭代搜寻变分模型最优解从而确定每个分解分量的频率中心和带宽，可以自适应地将信号分解成具有稀疏特性的分量[11-13]。

假设每个模态是具有中心频率的有限带宽，中心频率和带宽在分解过程中不断更新，VMD分解是寻求K个估计带宽之和最小的模态函数uk(t)，k∈{1,2,…,K}，各模态之和为输入信号f。通过以下步骤确定每个模态函数的带宽：

(1) 为了获得模态函数的解析信号，对每个模态函数uk(t)进行希尔伯特变换，即

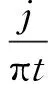
(1)

式中：t为时间，是大于0的正数；δ(t)为冲击函数；{uk(t)}={u1(t),u2(t),…,uK(t)}为分解得到的K个IMF分量。

(2) 对各模态解析信号预估中心频率e-jωkt进行混合，将每个模态的频谱调制到相应的基频带，即

(2)

式中，{ωk}={ω1,…,ωK}为各IMF分量uk(t)的中心频率。

(3) 计算以上解调信号的梯度的平方L2范数，估计出各模态分量的带宽。对应的约束变分模型表达式为

(3)

为了求取上述约束变分问题，引入二次惩罚因子α与Lagrange乘法算子λ(t)，其中α为足够大的正数，可在高斯噪声存在的情况下保证信号的重构精度，Lagrange算子使得约束条件保持严格性，扩展的Lagrange表达式为

L({uk(t)},{ωk},λ(t))=

(4)

(5)

式中，i∈{1,2,…,K}且i≠k。利用傅里叶等距变换，将式(5)转变到频域后用ω-ωk代替ω，并将得到的结果转换为负频率区间积分的形式，则优化问题的解为

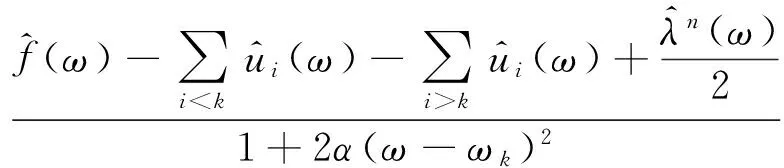
k∈{1,2,…,K}

(6)

根据同样的过程，求得中心频率更新方式

(7)

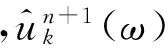
(2) 执行循环n=n+1；

(8)

式中，τ为时间常数，常取为0。

(5) 给定判别精度ε>0，重复上述步骤，直到满足迭代停止条件

(9)

1.2 峭度准则

峭度是反映随机变量分布特性的数值统计量，是归一化的4阶中心矩。

(10)

式中：μ、σ分别为信号的均值和标准差；E(x)为变量x的期望值。峭度系数对轴承早期故障比较敏感，当轴承没有任何故障时振动信号近似服从正态分布，而正态分布的峭度系数约等于3；当轴承逐步发生故障，工作表面出现损伤引起机械冲击时，其振动信号概率密度偏离正态分布，峭度系数值增加较快。所以可以推断出，峭度值越大说明这些IMF分量中包含有更多的冲击成分，对这些分量进行重构，则合成的信号峭度值会明显提高，包含的故障特征信息越多、故障特征越明显。

1.3 ICA算法基本原理

独立分量分析是一种盲信源分离技术。该方法是指在先验信息很少的情况下，仅通过观测信号来估计有用源信号的一种新型信号处理方法。模型为

假设x(t)=(x1(t),x2(t),…,xm(t))T为m个观测信号，s(t)=(s1(t),s2(t),…,sn(t))T为n个未知的相互独立的源信号，x(t)中各分量可由s(t)各独立信源线性表示，用矩阵可表示为

x(t)=As(t)

(11)

式中：x(t)为观测矩阵；s(t)为信号源矩阵；A为一个未知的满秩的m×n的混合系数矩阵(m≥n)。ICA的目的是要在信号源矩阵s(t)和系数矩阵A均未知的情况下，利用统计学途径获得分离矩阵W，使得分离矩阵满足

y(t)=Wx(t)=WAs(t)

(12)

式中，y(t)为源信号s(t)的估计。独立分量分析是最新提出的算法，其目的是使非高斯数据可以被线性表示。从线性变换角度来看，源信号即为相互独立的非高斯信号，也可称之为线性空间的基信号，而观测信号则是源信号的线性表示。ICA就是在源信号和系数矩阵A均未知的情况下，从混合信号中估计出有用的输入信号。该算法在统计独立的意义下对混合信号进行分离，从而提取出混合信号中的有用信号，相比传统的自适应滤波方法效果更好。

2 VMD-ICA联合降噪方法研究

由于轴承故障信号具有能量小、频带分布宽、易受其它震源干扰等问题，单独使用VMD算法对信号进行处理可能导致故障特征信息不能被完全提取出来。而独立分量分析目前的研究大都是基于多观测通道(即要求振动传感器的个数大于等于振动源信号。本文首先将故障信号进行VMD分解得到若干IMFs分量，然后依据峭度准则将IMF分量重构，引入虚拟噪声通道，由于引入信号包含原始信号先验信息，所以避免了盲目引入噪声信号导致处理结果不佳的影响。接下来对重构信号进行FastICA解混，最后对降噪后的信号进行能量算子解调，并将理论值与解调后的频率进行对比，识别故障类型。算法流程如图1所示，主要步骤为：

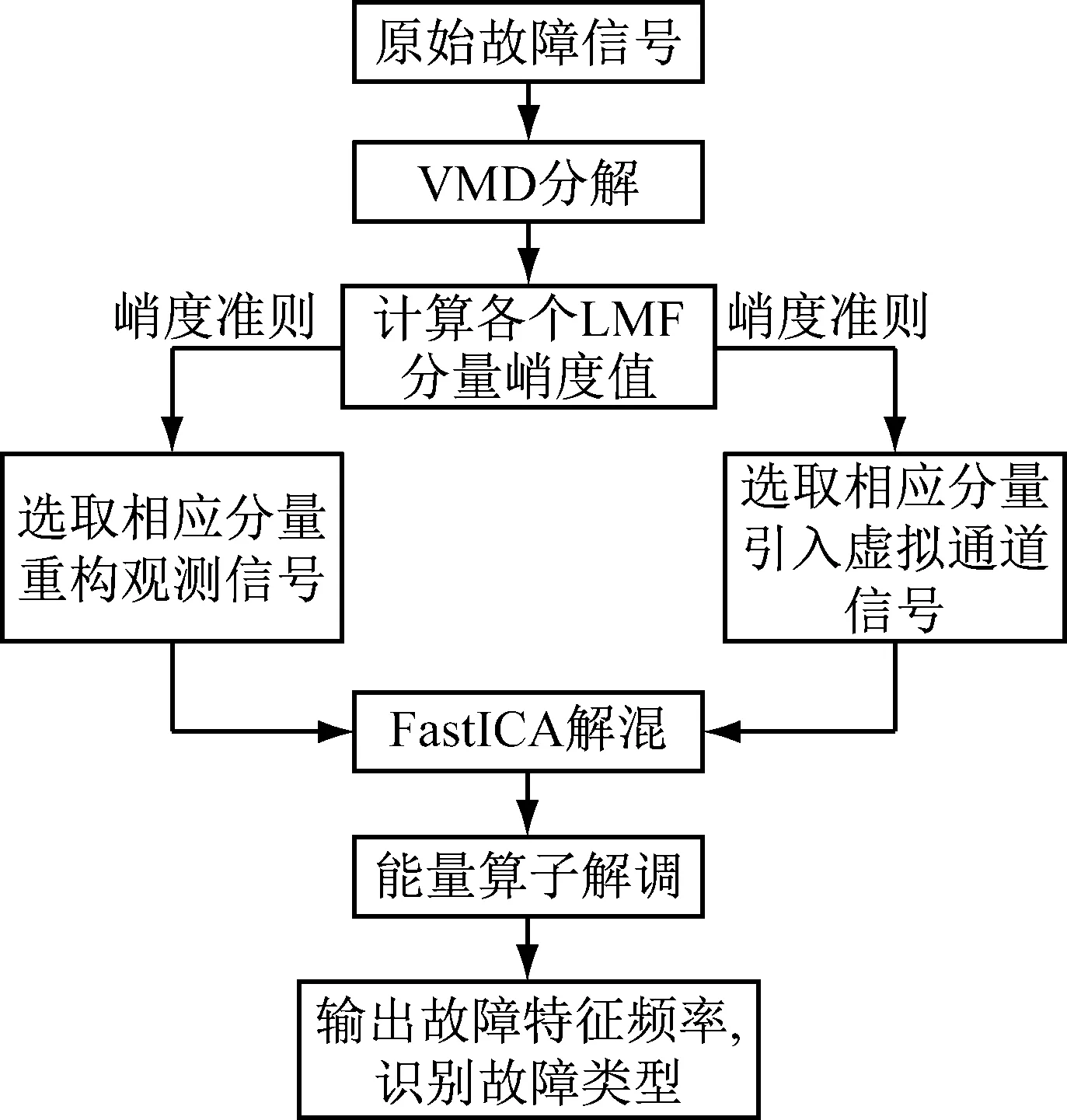
图1 VMD-ICA联合降噪算法流程图

步骤1 获取振动信号，初始化模态数K=2，惩罚因子α和带宽τ使用默认值，α=2 000，τ=0。

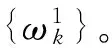
步骤3 判断中心频率是否相近，如果相近，则确定模态数为K=K-1，否则以模态数K=K+1继续进行步骤2。

步骤4 计算各个IMF分量的峭度值，依据峭度准则将IMF分量进行分组重构，得到观测信号s1(t)，并构造虚拟通道信号s2(t)。

步骤5 利用FastICA算法对步骤4得到的观测信号s1(t)和虚拟通道信号s2(t)进行解混，得到联合降噪后信号y1(t)。

步骤6 对步骤5得到的信号进行能量算子解调，提取故障特征频率，并与轴承特征频率的理论值进行对比，从而识别故障类型。

3 实验分析

为了验证本文提出方法在滚动轴承故障特征提取中的有效性，采用实际轴承内圈故障信号进行验证，实验平台如图2所示的QPZZ-Ⅱ旋转机械故障试验台。本实验测试参数及轴承技术参数如表1所示，由轴承特征频率理论计算公式可得到内圈故障频率f=37.5 Hz。滚动轴承内圈故障振动信号时域及频域波形如图3所示。

表1 轴承测试参数与技术参数

图2 QPZZ-Ⅱ旋转机械故障试验台

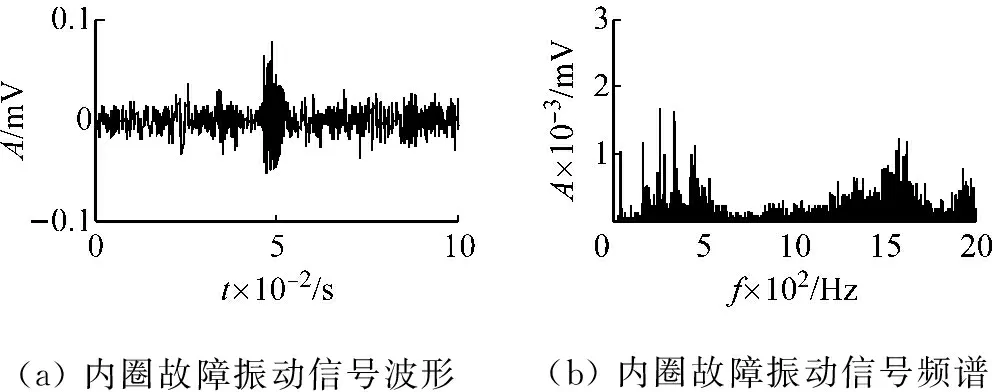
(a)内圈故障振动信号波形(b)内圈故障振动信号频谱

图3 内圈故障信号时域波形及频谱

Fig.3 Waveform and spectrum of the bearing inner fault

本文将从故障信号分解效果方面、信号去噪方面以及故障信号频率检测精度方面进行分析，并通过和LMD-ICA方法进行对比说明本文方法的有效性和优越性。

3.1 故障信号分解效果对比

为了防止出现欠分解和过分解现象，根据不同的K值对应的各个模态中心频率来确定分解次数。由表2可知当K=5时中心频率相差较大，出现了欠分解现象；而K=7时出现了中心频率相近的模态分量，发生了过分解现象。因此最终选取模态数K=6，分解结果如图4(a)所示。为了进行比较，将同一故障信号进行了LMD处理，结果如图4(b)所示。

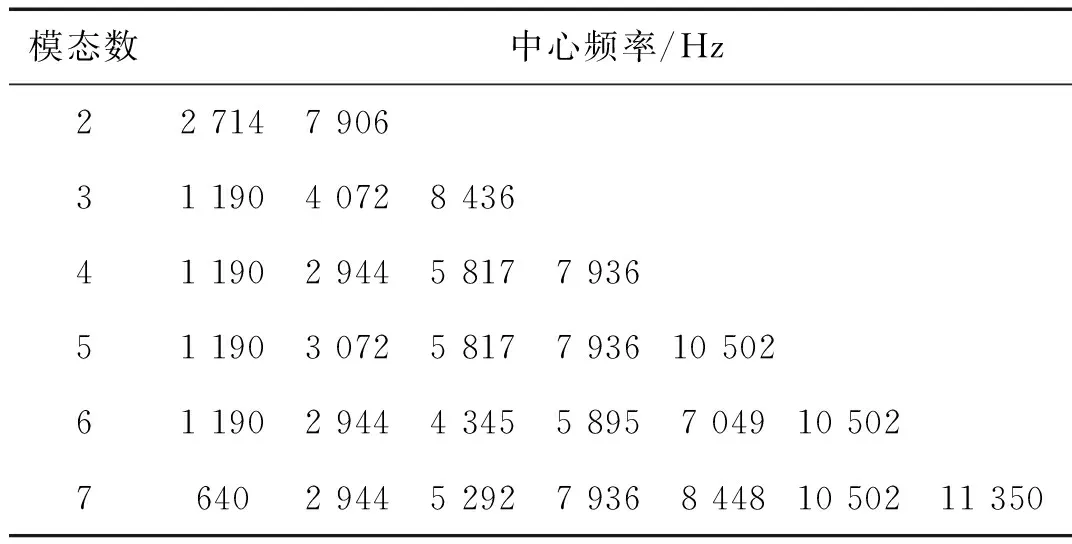
表2 不同K值各个模态分量的中心频率

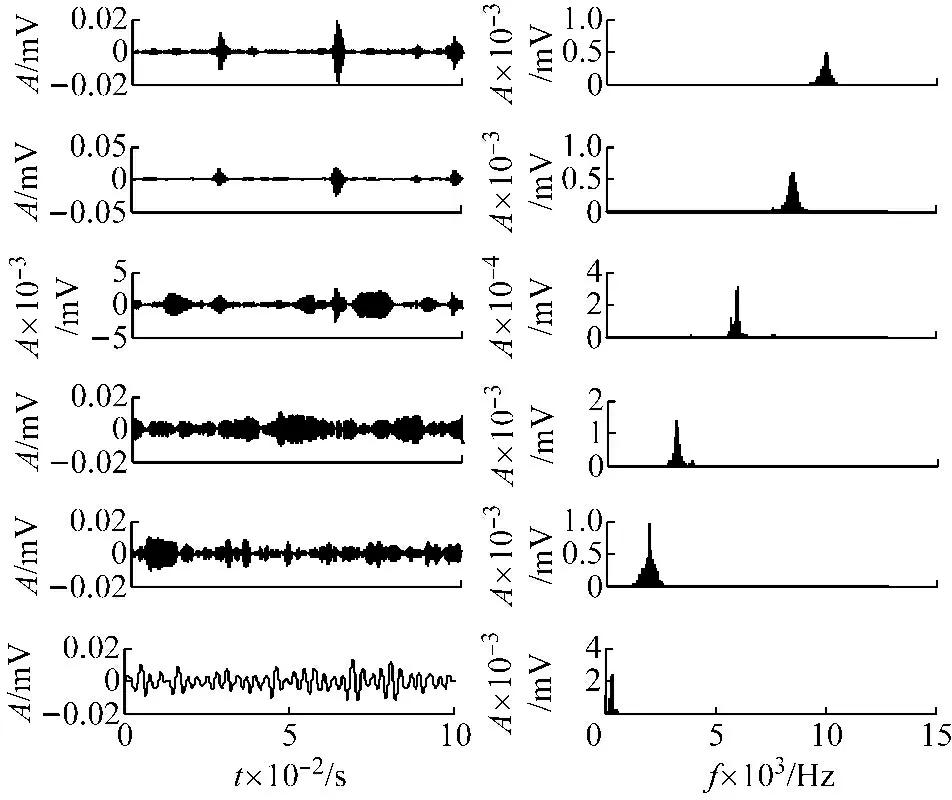
(a) VMD模态分量波形及频谱

(b) LMD模态分量波形及频谱

图4 轴承故障信号分解结果

Fig.4 Decomposition results of the original signal

从分解时域图中可以看出，VMD分解在一定程度上克服了LMD中存在的模态混叠和端点效应问题。而且从频谱图中可以看出，LMD的频段分离不是很分明，尤其是第一频谱分量，在整个频率范围内几乎都有分量，而VMD的各个频段的分离效果则较好。

3.2 重构信号去噪效果对比

3.2.1 实测信号分析

计算VMD分解后各个IMF分量的峭度值，如表3所示。由表3可知，IMF1、IMF2峭度值较大，说明其保留了原始信号中最多的冲击特征，故提取这两个IMF分量进行原始信号重构，剩余分量重构作为虚拟噪声通道，由于噪声通道的构成包含了原始信号本身部分的先验信息，避免了盲目选择噪声信号引起处理效果不佳的影响。重构信号如图5(a)、图5(b)所示，将重构信号利用FastICA方法进行分离，分离结果如图5(c)、图5(d)所示。将同一故障信号进行LMD分解后，计算各个分量的峭度值如表4所示，选取前三个分量进行重构，并利用FastICA方法进行分离，图6(a)～图6(d)为用LMD-ICA方法对信号进行处理得到的结果。

表3 IMFs分量峭度值

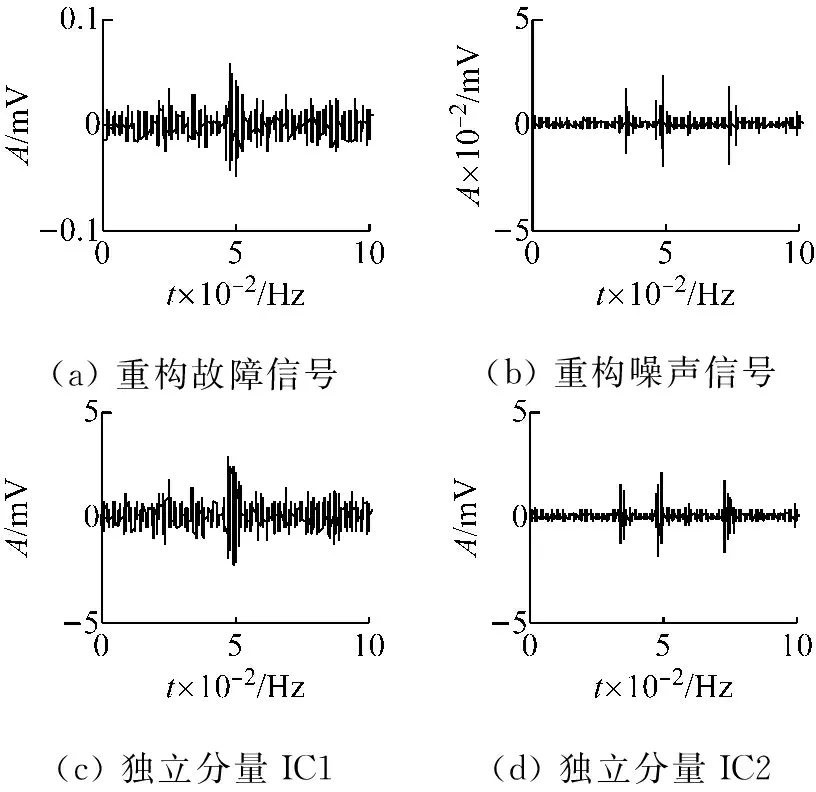
(a)重构故障信号(b)重构噪声信号(c)独立分量IC1(d)独立分量IC2

图5 本文所提方法分析结果

Fig.5 Analysis results with the proposed method

表4 IMFs分量峭度值

图5、图6定性地反映了以上两种方法的去噪效果，从图中可以看出，FastICA算法可有效地从混合信号中提取出有用信号，将噪声信号和有用信号分离开，由于ICA没有任何关于原始信号的先验知识，具有不确定性，所以解混后信号幅值可能不同，但是并不影响对信号的分析。

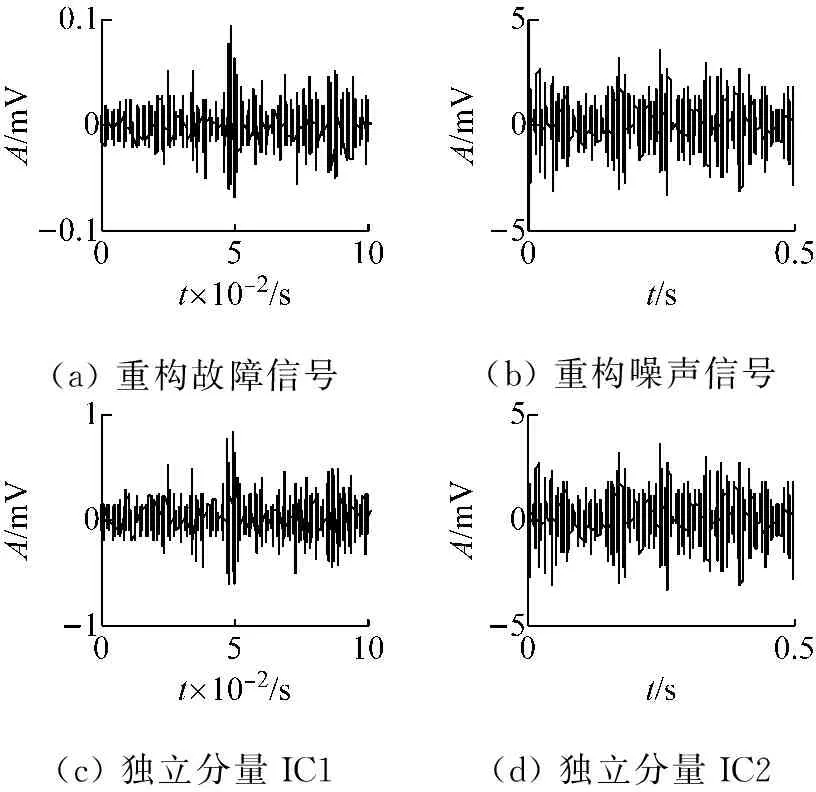
(a)重构故障信号(b)重构噪声信号(c)独立分量IC1(d)独立分量IC2

图6 LMD-ICA算法分析结果

Fig.6 Analysis results with LMD-ICA

为了定量地分析重构故障信号在以上两种方法降噪后的去噪效果，选取峭度值(K)、峰值信噪比(PSNR)作为降噪后效果的评价指标。峭度值说明了重构信号中包含的故障特征信息，峭度值越大则说明信号中故障信息越多；峰值信噪比则反映了信号的去噪能力，峰值信噪比越大则说明去噪效果越好。

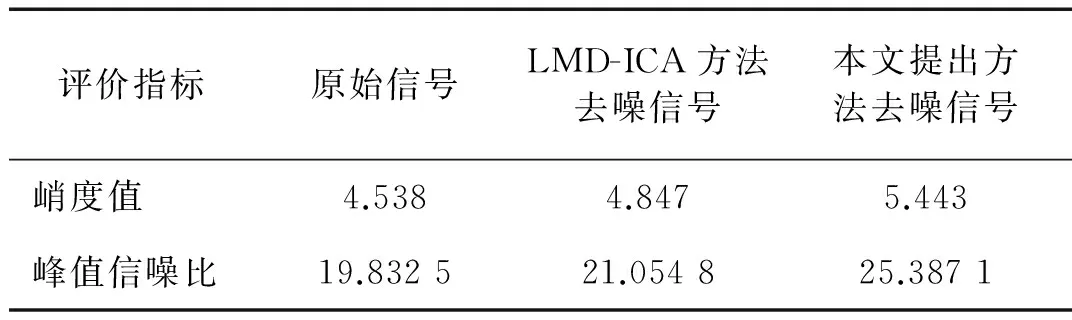
表5 降噪结果对比

3.2.2 仿真信号分析

在以上研究的基础上，构造如下仿真信号。其中，幅值A=1；衰减系数K=800；系统共振频率ωr=2×pi×1 000；u(t)为单位阶跃函数；设定信号的故障特征频率fr=128；滚珠和滚道之间微小滑动对故障特征频率的影响因子τi为0.01/fr-0.02/fr之间的随机数，采样频率为25 600 Hz，n(t)为白噪声。故障仿真信号的波形及频谱如图 7(a)、图7(b)所示。

(13)

相关系数反映了去噪后信号与原始信号之间整体波形的相似程度，在仿真信号中加入不同的信噪比，用相似度指标进一步比较以上两种方法的去噪性能，曲线图如图8所示。从图中可以看出，在不同信噪比情况下本文提出方法得到的去噪信号与原始信号相似度更高。尤其是在信噪比较低的情况下，本文提出方法仍能有效地降低噪声的干扰能力，在去噪方面效果更好。

(a)故障仿真信号波形(b)故障仿真信号频谱

图7 仿真信号波形及频谱

Fig.7 Waveform and spectrum of simulated signals

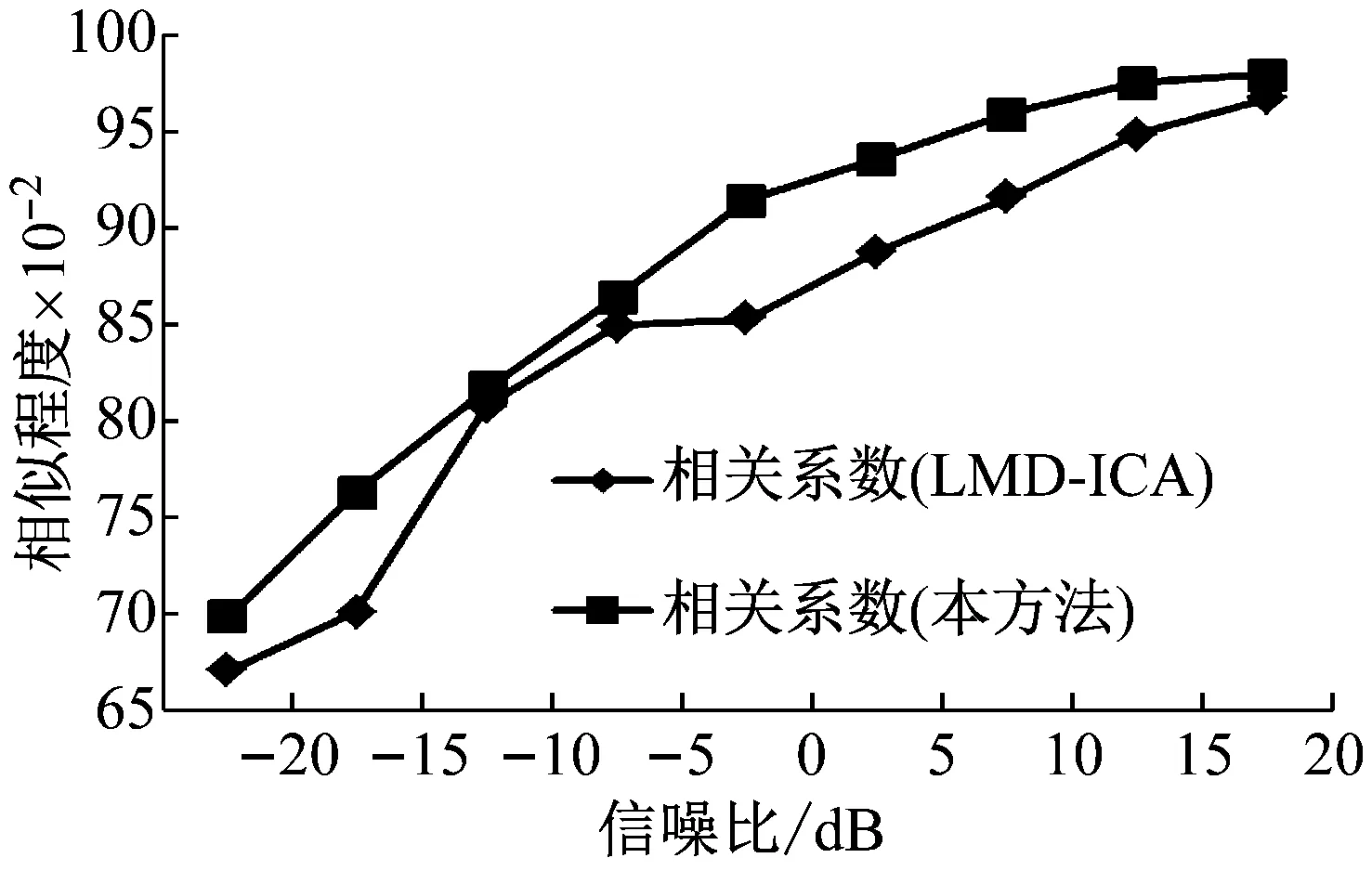
图8 信噪比-相似度曲线图

3.3 故障信号频率检测精度对比

将降噪后的信号分别进行能量算子解调得到相应能量谱，如图9(a)、图9(b)所示。图10(a)、图10(b)为用LMD-ICA方法得到的能量谱。依据文献[14]，本文定义故障频率检测精度为

(a)独立分量IC1能量谱(b)独立分量IC2能量谱

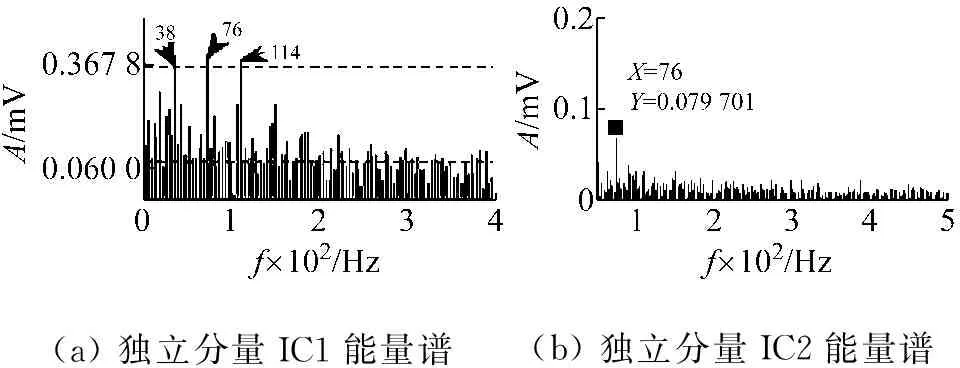
图9 本文所提方法分析结果

图10 LMD-ICA分析结果

Fig.10 The analysis results of LMD-ICA

4 结 论

振动信号中常受到噪声的影响，这些干扰导致故障特征提取困难，基于此本文提出了基于VMD和FastICA联合降噪的方法，并应用于轴承故障特征提取中，通过实测数据验证了提出方法的实用性和有效性，结论如下：

(1) 通过VMD将信号进行分解，引入了虚拟噪声通道，既解决了盲目引入噪声导致处理结果不佳的影响，又解决了ICA算法不能对单通道信号进行处理的问题。

(2) 通过峭度值选择相应分量重构，避免了盲目选择分量，造成故障特征信息丢失的弊端，同时对比了将重构信号进行ICA解混后的降噪效果，验证了本文提出方法在降噪方面的优越性。

(3) 相较于LMD-ICA方法，本文提出方法解决了去噪过程中丢失故障信息以及由于模态混叠导致噪声不能完全去除的问题。

[1] WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[2] 苏文胜，王奉涛，张志新，等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击，2010，29(3)：18-21.

SU Wensheng, WANG Fengtao, ZHANG Zhixin, et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings[J]. Journal of Vibration and Shock, 2010, 29(3): 18-21+201.

[3] 吴小涛，杨锰，袁晓辉，等. 基于峭度准则EEMD及改进形态滤波方法的轴承故障诊断[J]. 振动与冲击，2015，34(2)：38-44.

WU Xiaotao, YANG Meng, YUAN Xiaohui, et al. Bearing fault diagnosis using EEMD and improved morphological filtering method based on kurtosis criterion[J]. Journal of Vibration and Shock, 2015，34(2)：38-44.

[4] LIN Jinshan. Fault diagnosis of gearboxes based on the local mean decomposition method[J]. Intelligent Information Technology Application Association, 2011，141：559-563.

[5] 陈亚农，郜普刚，何田，等．局部均值分解在滚动轴承故障综合诊断中的应用[J]．振动与冲击，2012，31(3)：73-78．

CHEN Yanong, GAO Pugang, HE Tian, et al. Roller bearing comprehensive fault diagnosis based on LMD[J]. Journal of Vibration and Shock, 2012, 31(3): 73-78.

[6] 鞠萍华，秦树人，赵玲．基于LMD的能量算子解调方法及其在故障特征信号提取中的应用[J]．振动与冲击，2011,30(2)：1-4．

JU Pinghua, QIN Shuren, ZHAO Ling. Energy operator demodulating approach based on LMD and its application in extracting characteristics of a fault signal[J]. Journal of Vibration and Shock, 2011, 30(2): 1-4.

[7] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2013, 62(3): 531-544.

[8] HYVARINEN A, KARHUNEN J, OJA E. Independent component analysis[M]. New York: John Wiley, 2001.

[9] 张俊红，李林洁，马文朋，等. EMD-ICA联合降噪在滚动轴承故障诊断中的应用[J]. 中国机械工程，2013，24(11)：1468-1472.

ZHANG Junhong, LI Linjie, MA Wenpeng, et al. Application of EMD-ICA to fault diagnosis of rolling bearings[J]. China Mechanical Engineering，2013，24(11)：1468-1472.

[10] 姚家驰,向阳,李胜杨,等. 基于VMD-ICA-CWT的内燃机噪声源识别方法[J]. 华中科技大学学报(自然科学版)，2016，44(7)：20-24.

YAO Jiachi, XIANG Yang, LI Shengyang, et al. Noise sources identification method of internal combustion engine based on VMD-ICA-CWT[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition)，2016，44(7)：20-24.

[11] 武英杰，甄成刚，刘长良．变分模态分解在风电机组故障诊断中的应用[J]．机械传动，2015，39(10)：129-132．

WU Yingjie, ZHEN Chenggang, LIU Changliang. Application of variational mode decomposition in wind power fault diagnosis[J].Journal of Mechanical, 2015, 39(10): 129-132.

[12] 赵洪山，郭双伟，高夺.基于奇异值分解和变分模态分解的轴承故障特征提取[J].振动与冲击，2016，35(22)：183-188.

ZHAO Hongshan, GUO Shuangwei, GAO Duo. Fault feature extraction of bearing faults based on singlular value decomposition and variational modal decomposition[J].Journal of Vibration and Shock,2016,35(22):183-188.

[13] 唐贵基，王晓龙．参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]．西安交通大学学报，2015，49(5)：73-81．

TANG Guiji, WANG Xiaolong. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J]. Journal of Xi’an Jiaotong University, 2015, 49(5): 73-81.

[14] 熊伟,吕英华. 视频红信号频谱识别中波峰搜索算法研究[J]. 软件，2012，11：190-193．

XIONG Wei, LÜ Yinghua. Peak finding in the identify of video red signal spectrum[J]. Software,2012, 11: 190-193.

Application of VMD-ICA combined method in fault diagnosis of rolling bearings

MA Zengqiang, LIU Xiaoyun, ZHANG Junjia, WANG Jiandong

(Electrical and Electronics Engineering, Shijiazhuang Railway University, Shijiazhuang 050043, China)

In order to solve the problem of fault features of rolling bearings being difficult to extract, the signal analysis method of variational mode decomposition(VMD) combined with independent component analysis(ICA) was proposed here. At first, VMD was used to decompose a multi-component vibration signal into a number of quasi-orthogonal intrinsic mode functions (IMFs) to effectively suppress problems, such as, mode mixing, end effect and so on existing in LMD algorithm. Then the kurtosis criterion was used to choose the corresponding IMFs to be reconstructed, and to induce a virtual noise channel. Finally, the reconstructed signal was denoised again with the fastICA, the effective fault feature components were extracted and the fault types were identified. In order to verify the effectiveness of the proposed method, this method was applied in fault diagnosis of rolling bearings, its effect was compared with that of LMD-ICA algorithm. The results demonstrated that the proposed method can not only solve problems of losing fault information and not enough eliminating noise due to mode mixing in denoising process, but also extract fault feature frequencies more clearly and correctly.

rolling bearing; variational mode decomposition (VMD); noise reduction; independent component analysis (ICA); fault diagnosis

国家自然科学基金(11227201；11372199；11572206)；河北省自然科学基金(A2014210142)

2016-07-18 修改稿收到日期：2016-10-17

马增强 男，博士，教授，1975年生

柳晓云 女，硕士生，1991年生

TH165+.3

A

10.13465/j.cnki.jvs.2017.13.032