基于线调频小波路径追踪的滚动轴承故障特征提取

程卫东， 刘东东， 赵德尊

(北京交通大学 机械与电子控制工程学院，北京 100044)

基于线调频小波路径追踪的滚动轴承故障特征提取

程卫东， 刘东东， 赵德尊

(北京交通大学 机械与电子控制工程学院，北京 100044)

针对齿轮噪源以及变转速的工作条件双重干扰下的滚动轴承的故障诊断，提出了一种基于线调频小波路径追踪的滚动轴承故障特征提取方法。对混合信号进行Hilbert变换得到包络信号，并在满足采样定理的条件下对包络信号进行降采样；对降采样包络信号应用线调频小波路径追踪算法提取轴承的瞬时故障特征频率趋势线，再对轴承的瞬时故障特征频率趋势线和转速曲线进行等时间重采样，并求各时间点的计算瞬时故障特征系数；根据计算瞬时故障特征系数与轴承的外圈、内圈和滚动体的故障特征系数进行比较，完成故障诊断。通过处理仿真信号和实测信号证明了该方法在不对混合信号进行滤波和使用阶比分析的情况下，不仅能检测滚动轴承是否出现故障，而且能确定故障的发生位置。

齿轮噪源；变转速；轴承故障诊断；线调频小波；计算瞬时故障特征系数

齿轮噪源干扰和变转速的工作模式一直是困扰滚动轴承故障诊断的两大难题[1]。齿轮较大幅值的振动往往会掩盖轴承的故障冲击特征，齿轮啮合振动的基频、谐频谱线成分也影响轴承故障引起的共振频带的获取[2]。自适应噪声消除技术、周期与随机量分离技术、时域同步平均技术以及适应性噪声消除技术均曾被用来去除齿轮噪源的干扰[3-4]。文献[5]在不同的位置安装两个传感器，分别采集噪声背景下的轴承信号和背景噪声，将这两个信号分别作为自适应去噪系统的主输入和参考输入使用自适应消噪技术去噪，但是，这种去噪方法需要安装两个传感器，受到安装成本以及安装条件的限制。文献[6]指出周期与随机量分离算法要求保证轴承的转速不存在波动。张西宁等[7]运用同步平均的方法对信号进行处理，当轴承转速发生变化时，同步平均不能完全去除齿轮啮合、不对中产生的周期性噪声成分[8]。通过以上分析发现，现有的对于齿轮噪源影响的轴承故障的诊断基本都是先使用滤波技术去掉齿轮噪源的影响，再对剩余信号进行分析。滤波算法不仅复杂，效率较低，而且还可能需要安装额外的辅助设备，使设备检测成本提高。

目前，对于变转速工况下的滚动轴承的故障诊断常采用阶比跟踪技术[9-11]，将时域信号转化为角域信号，再进行处理。常用的阶比分析技术有硬件阶比跟踪和计算阶比跟踪两种。与硬件阶比跟踪技术相比计算阶比跟踪不需要采样率合成器、抗混叠跟踪滤波器、转速计等硬件设备[12]，因而引起了学者的广泛研究。然而，计算阶比分析也存在诸多弊端。例如，Saavedra等[13]证明计算阶比跟踪算法中插值算法存在不可避免的误差。等角度重采样时从时域到角域转变会涉及到大量高次方程，计算效率低，甚至出现无解情况，同样会存在误差。另外，阶比跟踪技术还存在包络畸变、幅值误差等问题。

近年,Candès等[14]提出了线调频小波路径追踪算法，该算法与常用提取故障特征频率的峰值搜索算法相比，不仅能更精确的提取信号各频率成分变化趋势线，而且还能根据需要选择提取不同频率范围内的频率成分变化趋势线。本文利用这一特性并结合分析信号在时频域的特点提出了不使用滤波技术和阶比跟踪技术的基于线调频小波路径追踪的滚动轴承故障特征提取方法。

具体方法：首先，对原始振动信号进行Hilbert变换得到包络信号，并在满足采样定理的条件下对包络信号进行降采样；然后，对降采样包络信号应用线调频小波路径追踪算法提取故障轴承的瞬时故障特征频率(Instantaneous Fault Characteristic Frequency，IFCF)趋势线，再对轴承的IFCF趋势线和转速曲线进行等时间重采样，并求各时间点的计算瞬时故障特征系数；最后，根据计算瞬时故障特征系数与轴承的外圈、内圈和滚动体的故障特征系数进行比较，完成故障诊断。通过处理仿真信号和实验信号来证明该方法在不对原始信号进行滤波和使用阶比分析的情况下，不仅能检测滚动轴承是否出现故障，而且能确定故障发生位置。

1 滚动轴承的故障特征频率及特征系数

当滚动轴承的外圈、内圈或者滚动体出现凹坑或裂纹时，故障点与其接触点会产生冲击，由于系统的衰减特性，形成高幅值而快速衰减的冲击响应。根据轴承结构，尺寸参数以及转频可以计算轴承的各部分的故障特征频率FCF(Fault Characteristic Frequency)[15-16]

外圈故障特征频率fo

(1)

内圈故障特征频率fi

(2)

滚动体故障特征频率fb

(3)

式中：N为滚动体个数；fr为轴承内圈转频；d为滚动体直径；D为节圆直径；φ为接触角。

根据各部分的故障特征频率便可以得到故障特征系数(Fault Characteristic Coefficient, FCC)

(4)

(5)

(6)

由式(4)、式(5)和式(6)可以看出FCC的大小只与滚动轴承的参数有关，不会随着转速以及其他因素的变化而变化，根据这个特性，在滚动轴承的故障诊断的过程中我们只需要求出FCC并与使用轴承各部分的FCC比较，不仅能判断出轴承是否发生故障还能确定故障位置。由于FCF以及转速曲线的获取都涉及插值估计等函数，因此，求出的每个时间点的FCC不可能为定值，应该与实际FCC有一定误差。本文将使用线调频小波路径追踪获取的瞬时故障特征频率与对应点转速的比值称为计算瞬时故障特征系数(Calculating Instantaneous Fault Characteristic Coefficient, CIFCC)，进而通过分析求得的CIFCC来判断轴承故障的情况。

2 线调频小波路径追踪算法

线调频小波路径追踪原理是将信号时间长度以二进制划分为动态的时间支撑区，从定义的chirplet原子库中寻找各动态支撑区相关性最大的原子并采用最佳路径连接的算法逐一连接，自适应的寻找信号中相关性最大的信号分量的瞬时频率变化趋势线。具体算法如下：

建立chirplet原子库

(7)

式中:I为动态支撑区间，I=[kN2-j,(k+1)N2-j]×Δt；k为动态区间的序号，k=0,1,…,2j-1；N为待分析信号的采样点数；j动态支撑区间的尺度系数，j=0,1,…,log2N-5；1I(t)为矩形窗函数，即t∈I时，1I(t)=1,t∉I时，1I(t)=0；aμ为调频率系数；bμ为频率偏置系数；根据采样定理，aμt+bμ为动态支撑区间内瞬时频率，应小于fs/2。

定义分析信号为信号与原子库中所有原子的内积，即

(8)

式中:Δt为采样时间间隔；n为t时刻采样点数。

在建立的原子库中寻找一组原子连接，使其既能覆盖整个分析信号的长度，又能使分析信号在时间支撑区域上有最大的投影系数，支撑区间内最大投影系数为

(9)

定义最大投影系数kI在时间支撑区I内代表的信号分量为dI(t)，得

(10)

连接最大投影系数kI使得信号分量dI(t)信号具有最大的总能量，即

(11)

式中，Π应覆盖整个时间长度且不重叠。

由此获得最佳路径连接算法：

(1) 初始化 取e(i)=0，pred(i)=0，其中，e(i)为选取i-1个动态时间支撑区的最大投影系数对应的总能量和，pred(i)为连接到第i个动态时间支撑区的前置支撑区的序号。

e(i)+d(i)>e(k)

(12)

则令

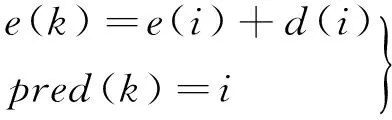
(13)

该连接方法能确保基原函数的组合与待分析信号的相似度最高，而动态支撑区Π内的瞬时频率为aμt+bμ，线性连接各个动态支撑区的瞬时频率就获得了待分析信号分解信号的瞬时频率。

3 基于线调频小波路径追踪的滚动轴承故障特征提取方法

从第2节的线调频小波路径追踪的算法可以看出，线调频小波路径追踪算法与峰值搜索算法不同，应用线调频小波路径追踪算法可以提取选定频率范围内的复杂信号中的频率成分的变化趋势线。齿轮的啮合频率为齿轮所在轴的整齿数倍，为了防止齿轮加工的过程中出现“根切现象”，齿轮的齿数一般大于等于17。而如式(4)～式(6)所示，轴承的故障特征频率与转频的比值为故障特征系数，故障特征系数一般很小，所以，齿轮啮合频率及其倍频不会影响故障特征频率的提取。正常齿轮的振动无调幅调频现象，不会出现啮合频率被转频及其高倍频调制的现象，对齿轮振动信号进行Hilbert变换产生的包络信号不会在低频部分产生转频及其倍频[17]。因此，齿轮的啮合频率与倍频及其包络信号均不会对轴承低频的包络信号中的故障特征频率的提取产生干扰。鉴于此，提出了基于线调频小波路径追踪的滚动轴承的故障特征提取方法。

图1给出了具体算法如下：

(1) 对原始振动信号进行Hilbert变换得到包络信号，并在满足采样定理的条件下对包络信号进行降采样；

(2) 根据实验轴承的各部分的FCC和转速曲线计算FCF的变化范围，并应用线调频小波路径追踪算法对降采样包络信号提取故障轴承的IFCF趋势线；

(3) 为了使IFCF趋势线的点与转速曲线点在时间上一一对应，对IFCF趋势线和转速曲线进行等时间重采样(这里的重采样区别于阶比分析需要的等角度重采样，不涉及信号的时域到角域的转换，只是用到简单的一次朗格朗日插值函数，而且一般重采样100个点就能满足需要，避免了引言所说的等角度重采样需要解大量高次方程等缺陷)；

(4) 根据重采样的IFCF趋势线和转速曲线求各时间点的计算瞬时故障特征系数；

(5) 根据计算瞬时故障特征系数的分布范围与轴承的外圈、内圈和滚动体的FCC进行比较，判断轴承是否发生故障。

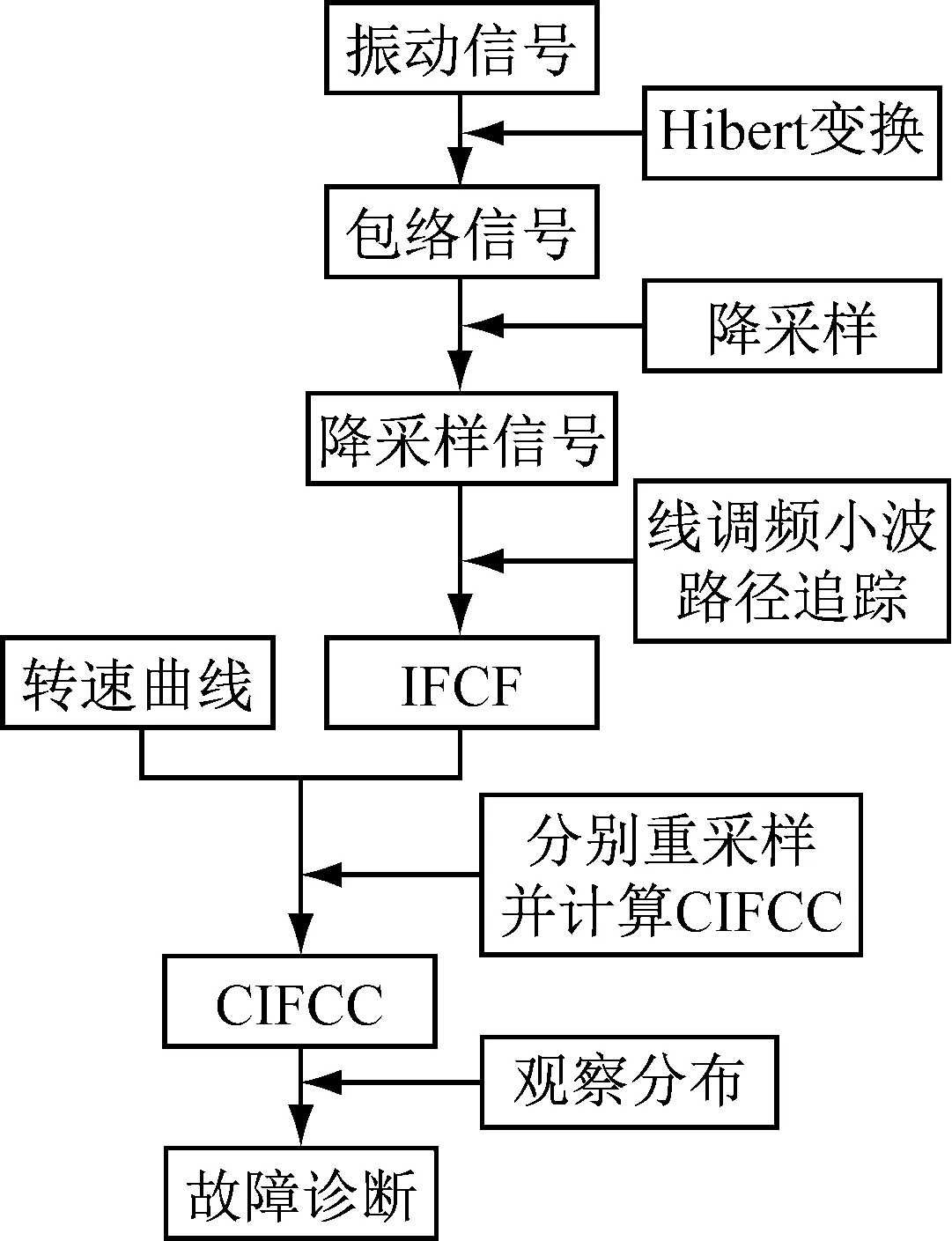
图1 基于线调频小波路径追踪的滚动轴承故障诊断方法流程图

Fig.1 Flowchart of rolling bearing fault diagnosis based on chirplet path pursuit

4 仿真信号分析

为了验证提出诊断方法的有效性，对滚动轴承的仿真信号进行分析。模拟滚动轴承的外圈出现故障，故障特征系数C0=3，滚动轴承内圈的转速如图5(实线)所示随时间成线性变化为v(t)=10t+5(rps)，轴承转过角度与时间之间的关系

(14)

式中,θi=i/C0(i=1,2,…,k)，由θi=i/C0和式(14)可以求得每个冲击对应的时标Ti。

该混合信号主要由故障轴承的冲击成分xbearing、齿轮啮合振动产生信号成分xgear和白噪声成分n(t)三部分构成，如式(15)所示。

x(t)=xbearing+xgear+n(t)

(15)

本文改进了匀转速工况下滚动轴承的振动信号的仿真模型[18]，构造变转速工况下故障滚动轴承振动信号的仿真模型

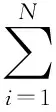
φω)×u(t-iT-τi)

(16)

齿轮振动信号的仿真模型

φm)

(17)

式中:Ai与Am分别为轴承和齿轮信号第i和m个冲击时的最大幅值，简化该幅值与时间成线性关系；fr为共振频率；fz(t)为齿轮转频随时间变化规律；参考轴承转速的时间浮动，定义滑移常数λ；轴承和齿轮信号的初相角φω、φm均设定为0；齿轮箱主动轮和外圈故障轴承同轴，齿数为Z，单级传动，其参数设定如下表所示。

根据以上仿真模型和参数得到如图2所示的时域波形图。对仿真信号做短时傅里叶变换(Short-time Fourier Transform,STFT)得到如图3所示的时频图，从时频图可以看到齿轮啮合频率及其倍频与轴承共振频率产生交叉，不能通过带通滤波直接获得共振频率。图4给出了谱峭度图，从谱峭度图中看出最大峭度值出现在尺度为7，中心频率为119 Hz处，而不是在中心频率为2 000 Hz(共振频率)处，这也直观反应了利用谱峭度滤波的限制。分析得知，通过滤波处理以获得共振频率有一定难度。因此，这里试图避开使用滤波处理仿真信号。

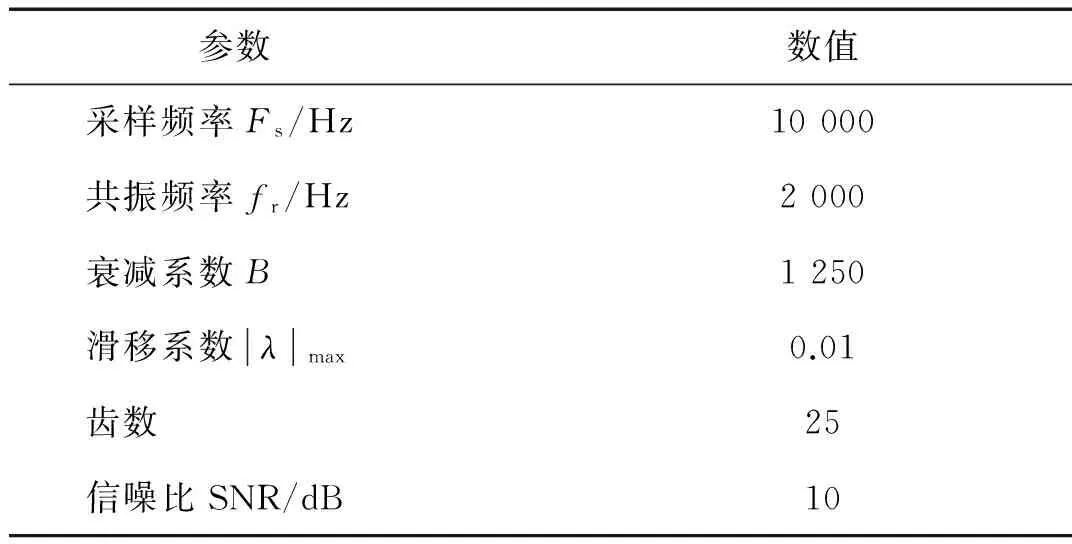
表1 振动信号仿真模型参数

根据轴承转速变化范围5～25 Hz(如图5所示)和C0=3，求得故障特征频率的变化范围为15～75 Hz，为了提高线调频小波路径追踪算法处理的效率，对经过Hilbert变换得到的包络信号进行降采样，降采样后的采样频率为1 024 Hz，通过计算，降采样后的采样频率仍满足采样定理。设置频率提取范围为10～80 Hz，应用线调频小波追踪算法得到如图5所示的IFCF趋势线。对IFCF趋势线与转速曲线进行重采样处理(取100个点)并求各时间点的CIFCC，做如图6所示的CIFCC分布范围的柱状图，81%的点数落在了3±0.015范围内并且100%的点落在了3±0.045范围内，恰好对应设置的外圈的FCC(C0=3)。因为同一轴承的外圈、内圈以及滚动体的FCC不同，所以可以判断滚动轴承是否发生故障以及故障发生的位置。对仿真信号的分析验证了本文提出方法的有效性。

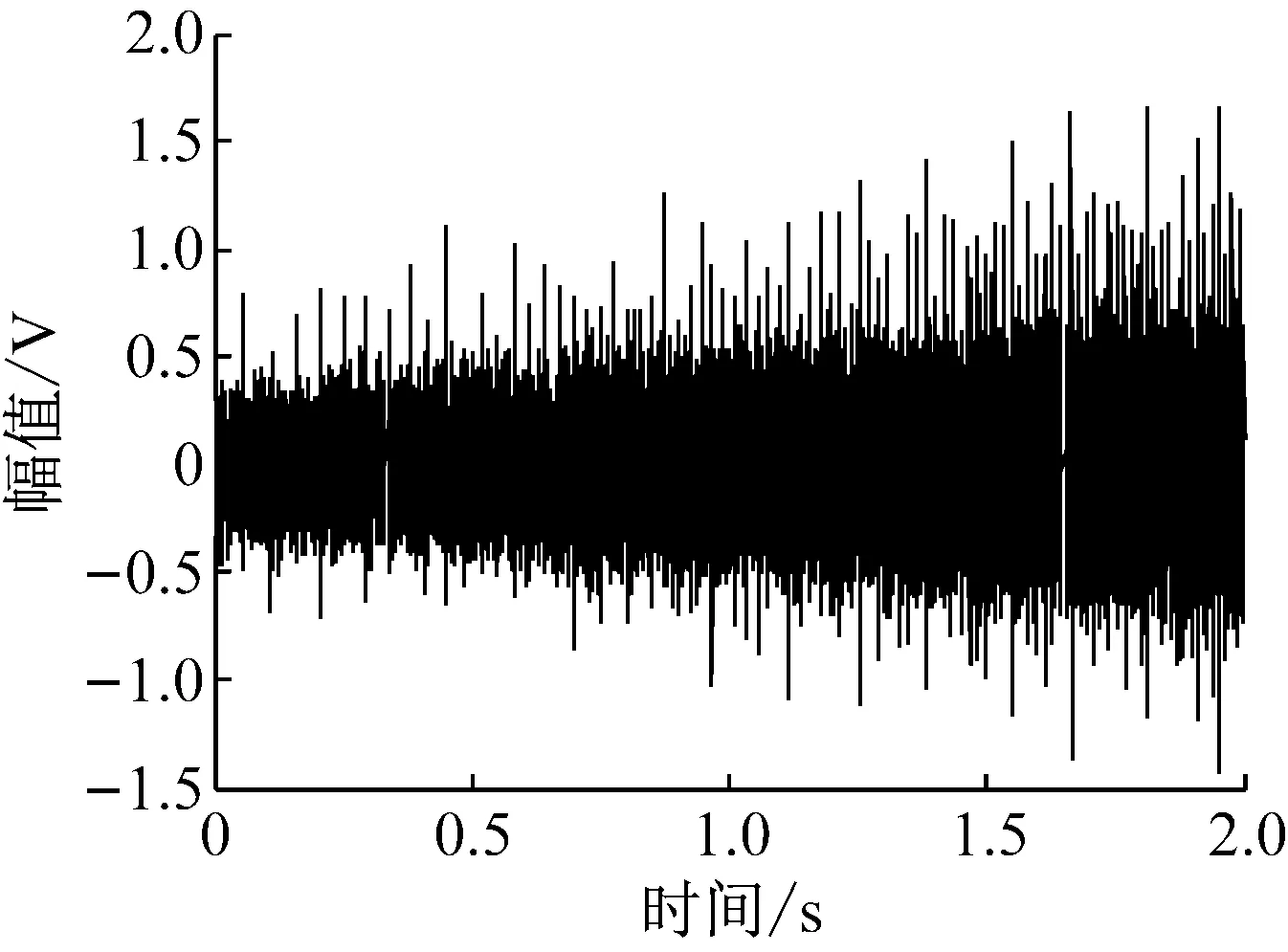
图2 仿真信号时域波形图

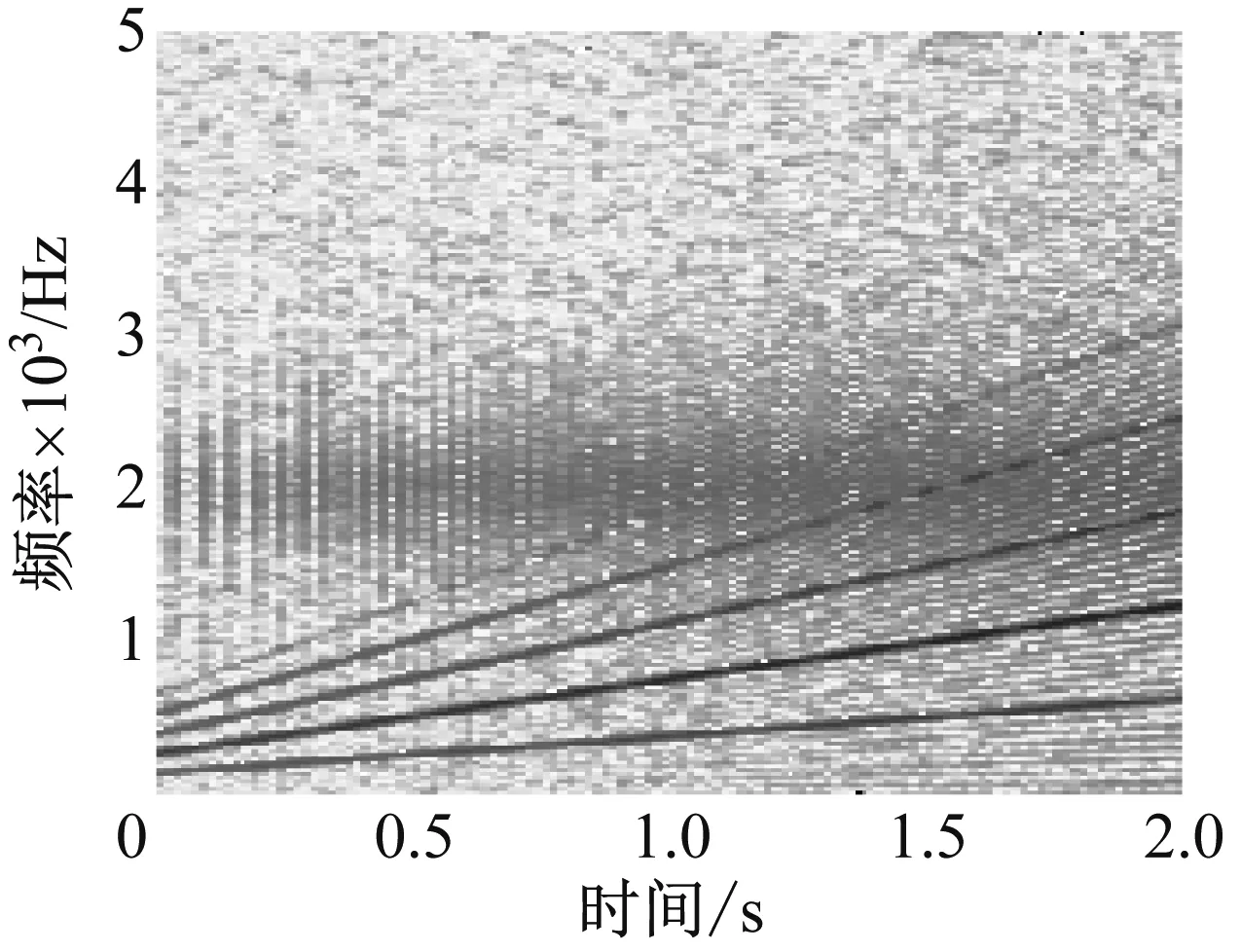
图3 仿真信号时频谱

Fig.3 The time-frequency representation of simulated signal

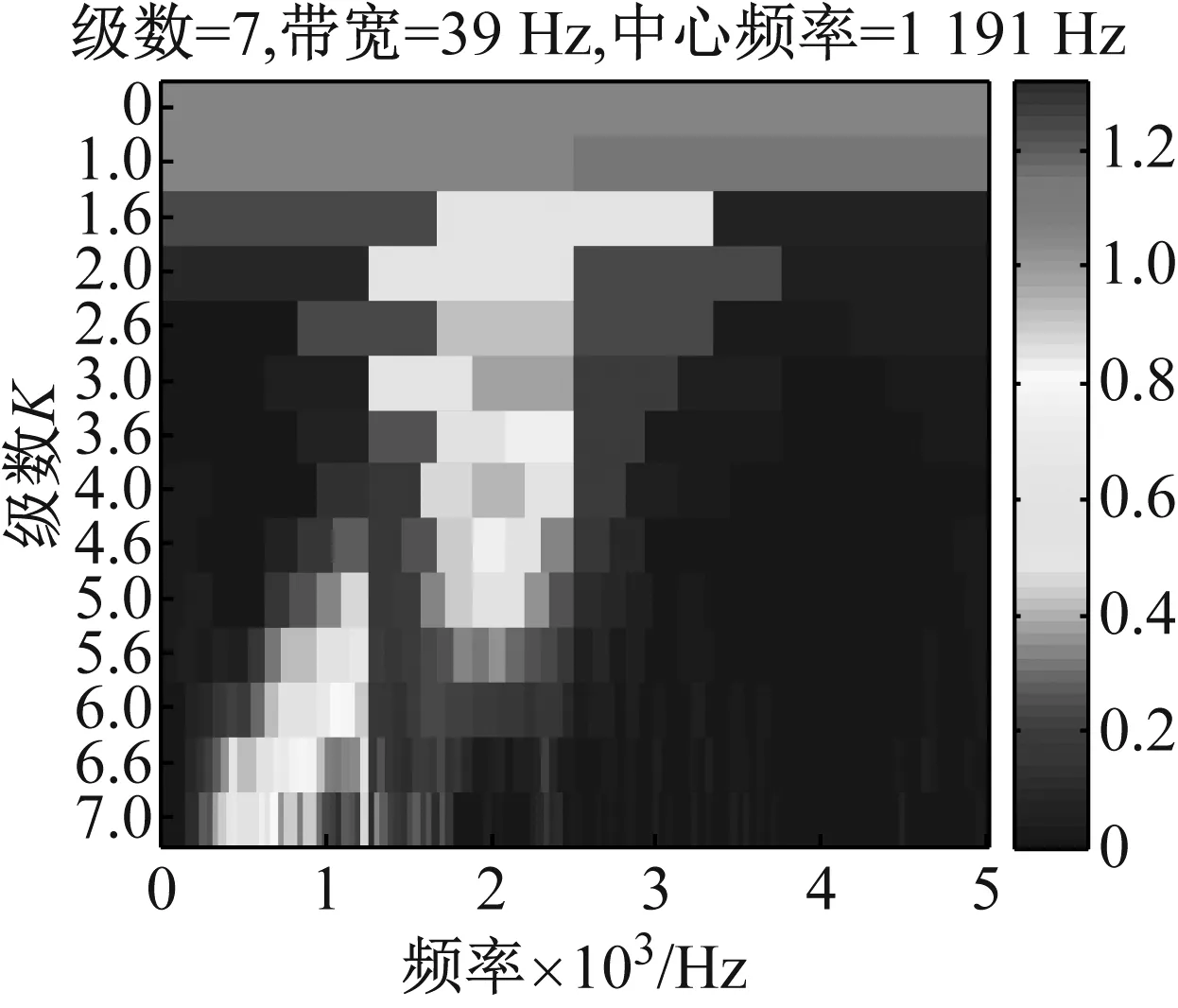
图4 仿真信号谱峭度图

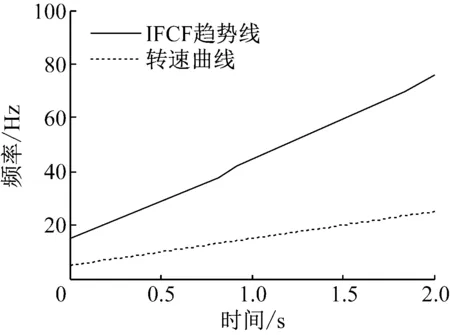
图5 仿真信号转频与IFCF趋势线

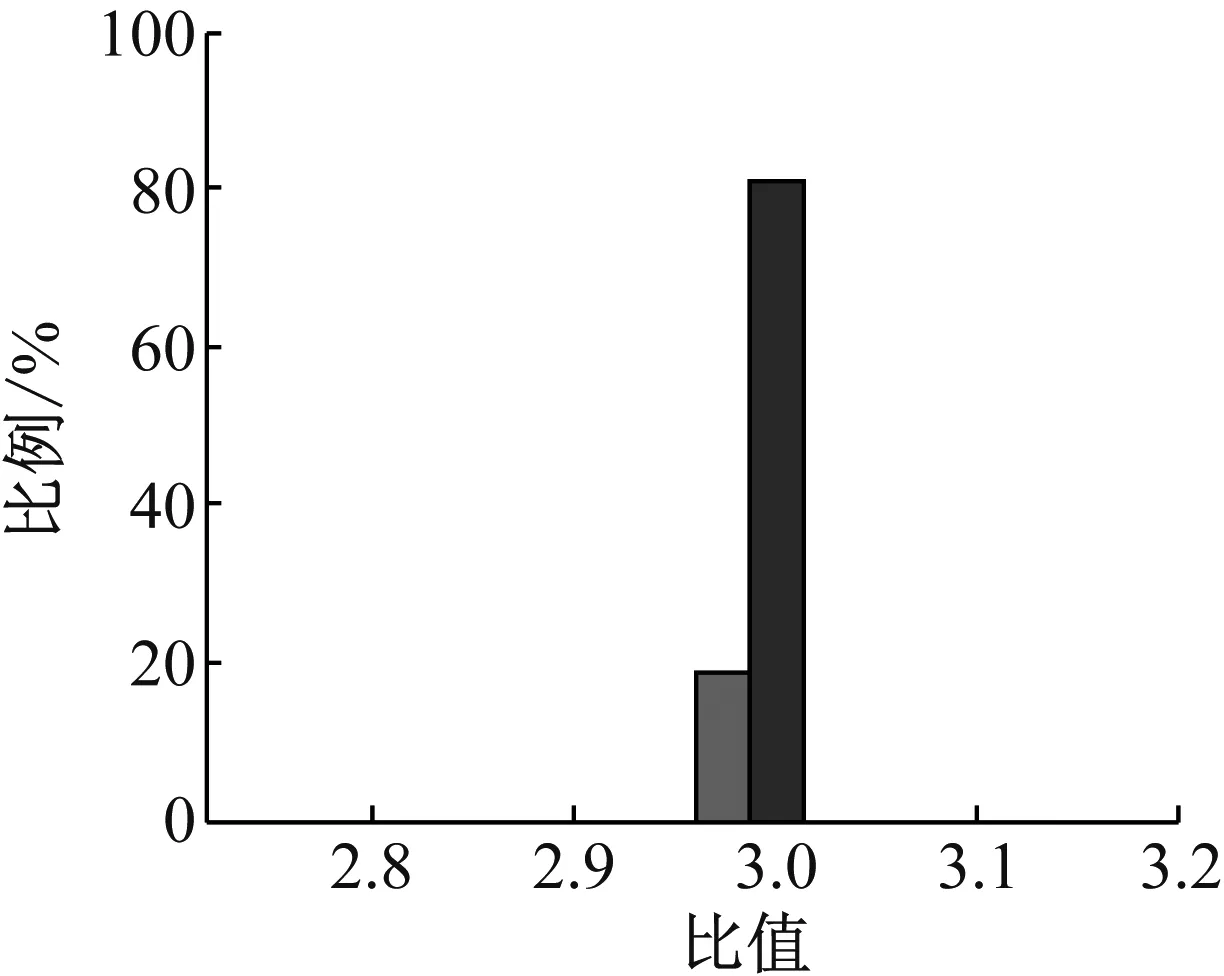
图6 仿真信号的计算瞬时故障特征系数分布图

5 实测信号验证

利用滚动轴承实验台测取的外圈故障滚动轴承和内圈故障滚动轴承的振动信号对本算法进一步验证。其中，与轴承同轴的齿轮齿数为15，实验轴承的参数如表2所示。

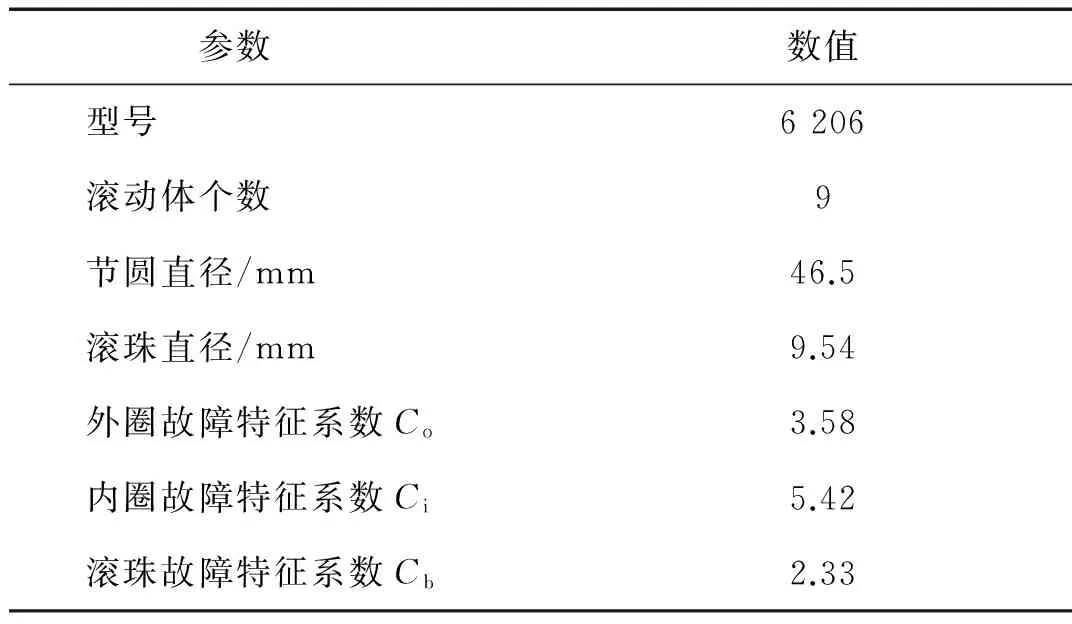
表2 滚动轴承结构参数

采集系统的采样率为24 000 Hz，截取时间段为2 s的数据，转速如图10所示,变化范围41～94 r/min。图7和图8给出了实验信号的时域波形图和时频图，从时频图可以明显的看到齿轮啮合频率及其倍频与轴承共振频率交叉，不能直接通过带通滤波直接提取共振频率。图9给出了仿真信号的谱峭度图，从谱峭度图中看出最大峭度值出现在尺度7，中心频率为2 390 Hz处，而不是在中心频率为6 000 Hz(共振频率)处，这也直观反应了利用谱峭度滤波的限制。

对经Hilbert变换得到包络信号进行降采样，降采样后的采样频率为2 048 Hz。设置频率提取范围为220～510 Hz，应用线调频小波追踪算法得到如图10所示的IFCF趋势线。对IFCF趋势线与转速曲线进行重采样处理(取100个点)并求各时间点的CIFCC，做如图11所示的CIFCC分布范围的柱状图，81%的点数落在了3.58±0.02范围内并且100%的点落在了3.58±0.06范围内，恰好对应轴承的外圈的故障特征系数C0=3.58，由此可以判断轴承的外圈出现故障。

通过处理内圈故障滚动轴承振动信号进一步验证本文算法的有效性，图12为内圈故障轴承振动信号的时域波形图，利用本文算法对该振动信号进行处理，得到如图13所示的CIFCC分布柱状图，观察发现，100%的点落在了5.42±0.04范围内，恰好对应轴承的内圈的故障特征系数C0=5.42，由此可以判断轴承的内圈出现故障。

图7 外圈故障滚动轴承信号时域波形图

图8 外圈故障滚动轴承信号时频谱

Fig.8 The time-frequency representation of outer faulty bearing signal

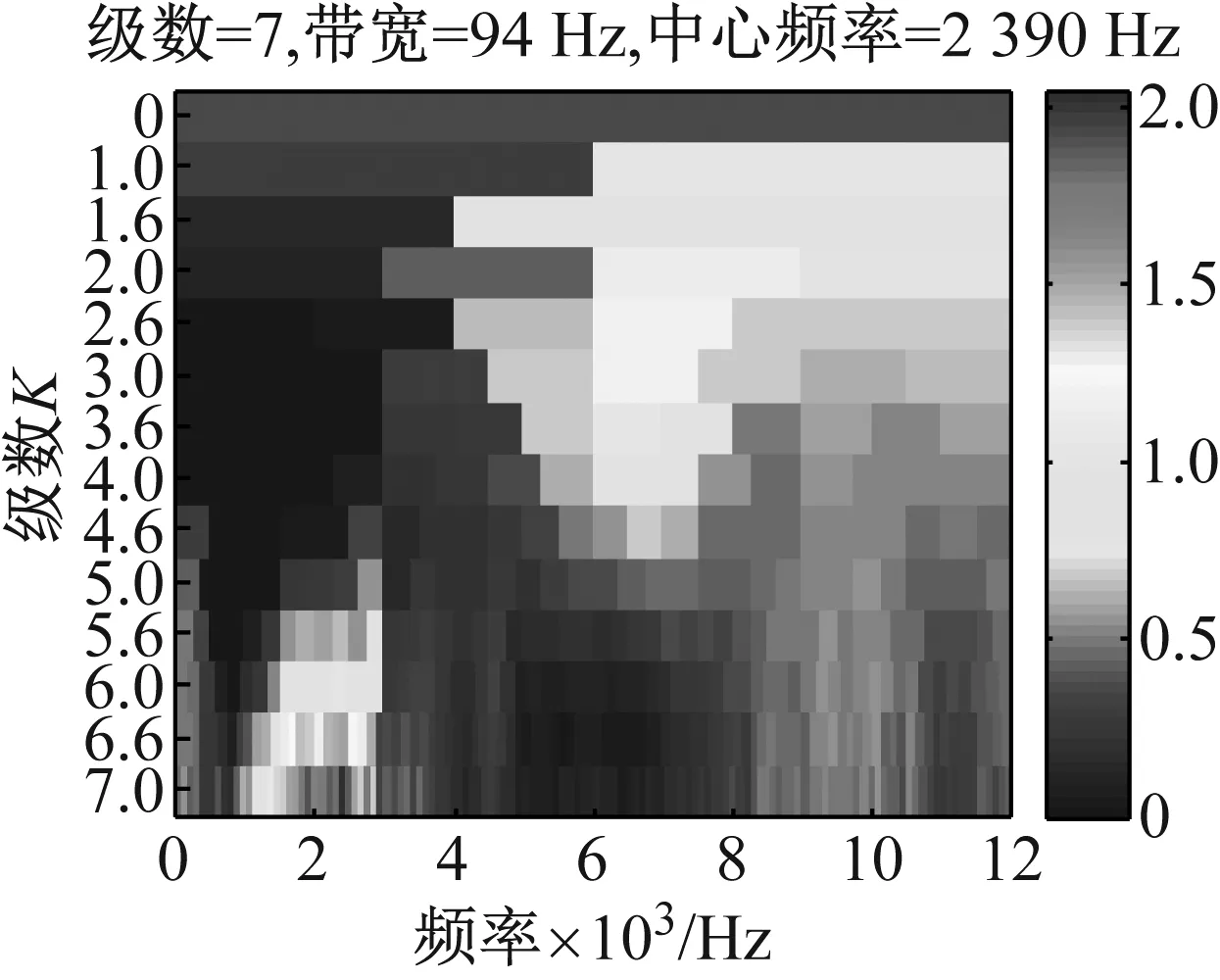
图9 外圈故障滚动轴承信号谱峭度图

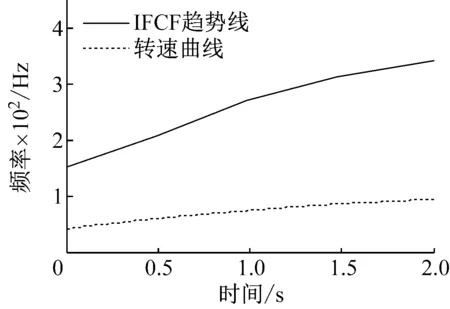
图10 外圈故障轴承信号转频与IFCF趋势线

Fig.10 The curve of outer faulty bearing signal rotating frequency and FCF

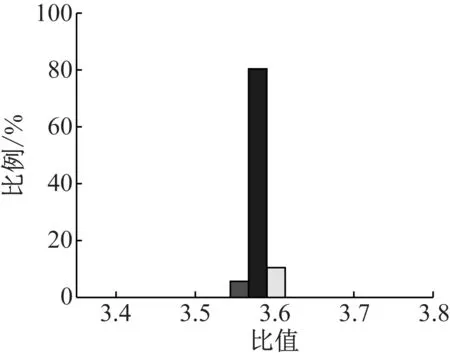
图11 外圈故障轴承信号的计算瞬时故障特征系数分布图

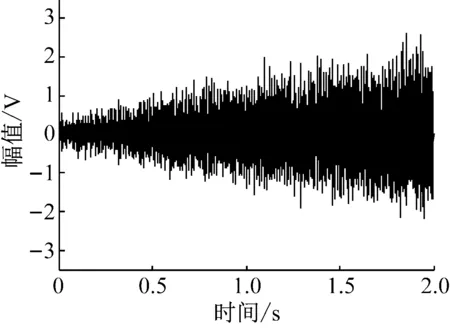
图12 内圈故障滚动轴承信号时域波形图

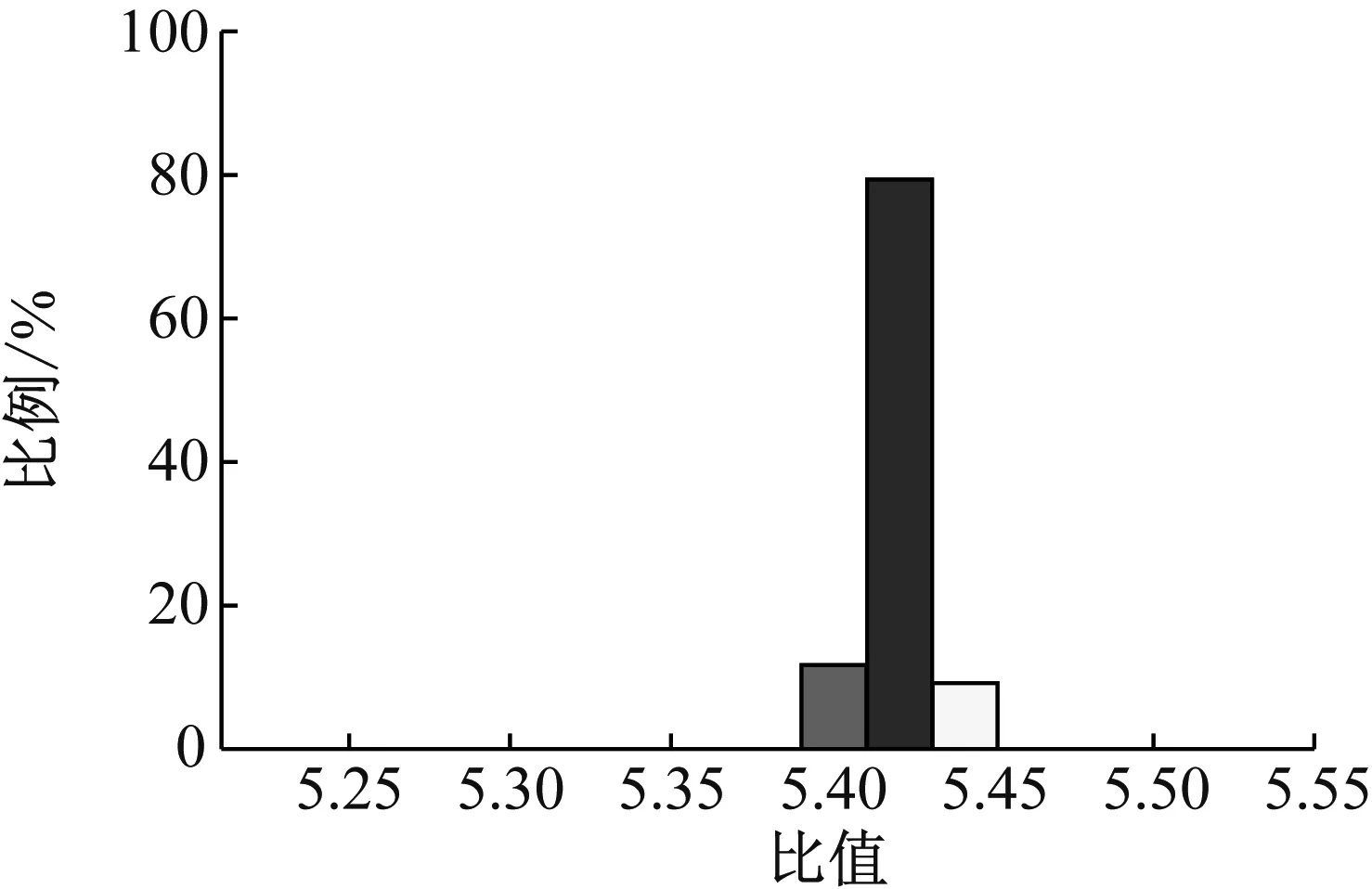
图13 内圈故障轴承信号的计算瞬时故障特征系数分布图

6 结 论

对混合信号经过Hilbert变换和降采样处理后得到降采样包络信号，然后利用线调频小波路径追踪算法可以从降采样包络信号中提取轴承的IFCF趋势线。根据IFCF趋势线与转速曲线可以得到CIFCC，通过分析CIFCC的大小分布能够判断轴承发生故障的位置。整个处理过程没有使用滤波算法和阶比跟踪技术，避免了滤波算法使用的局限性和因安装辅助设备产生的成本的提高以及阶比跟踪技术的不足，为齿轮噪源影响下的变转速工况下滚动轴承的故障诊断提供了一种新思路。

[1] ZHAO Dezun, LI Jianyong, CHENG Weidong. Feature extraction of faulty rolling element bearing under variable rotational speed and gear interferences conditions[J]. Shock and Vibration, 2015(3): 1-9.

[2] 王天杨，李建勇，程卫东. 基于改进的自适应噪声消除和故障特征阶比谱的齿轮噪源干扰下变转速滚动轴承故障诊断[J]. 振动与冲击, 2014, 33(18): 7-13.

WANG Tianyang,LI Jianyong,CHENG Weidong. Fault diagnosis of rolling bearing under a variable rotational speed and gear vibration noise based on revised ANC algorithm and FCO spectrum[J]. Journal of Vibration and Shock, 2014, 33(18): 7-13.

[3] ANTONI J, RANDALL R B. Unsupervised noise cancellation for vibration signals:part II-a novel frequency-domain algorithm[J]. Mechanical Systems and Signal Processing, 2004, 18(1): 103-117.

[4] ANTONI J, RANDALL R B. Unsupervised noise cancellation for vibration signals:Part I-evaluation of adaptive algorithms[J]. Mechanical Systems and Signal Processing, 2004, 18(1): 89-101.

[5] CHATURVEDI G K, THOMAS D W. Bearing fault detection using adaptive noise canceling[J]. Journal of Mechanical Design, 1982, 104(2): 280-289.

[6] RANDALL R B, SAWALHI N. A comparison of methods for separation of deterministic and random signals[J].Condition Monitoring, 2011,1(1):11-43.

[7] 张西宁，吴婷婷，徐进杰. 变转速齿轮箱振动信号监测的无键相时域同步平均方法[J].西安交通大学学报, 2012, 46(6): 111-116.

ZHANG Xining, WU Tingting, XU Jinjie,et al. Time-domain synchronous average method without key-phase signal for vibration monitoring of variable speed gearbox[J]. Journal of Xi’an Jiaotong University, 2012, 46(6): 111-116.

[8] BORGHESANI P, RANDALL R B. Application of cepstrum pre-whitening for the diagnosis of bearing faults under variable speed conditions[J]. Mechanical Systems and Signal Processing, 2013, 36(2): 370-384.

[9] BONNARDOT F, BADAOUI M E, RANDALL R B, et al. Use of the acceleration signal of a gearbox in order to perform angular resampling(with limited speed fluctuation)[J]. Mechanical Systems and Signal Processing, 2005, 19(4): 766-785.

[10] 郭瑜，秦树人. 无转速计旋转机械升降速振动信号零相位阶比跟踪滤波[J]. 机械工程学报，2004, 40(3): 50-54.

GUO Yu, QIN Shuren. Tacholess order tracking filtering for run-up or coast down vibration signal of rotating machinery based on zero-phase distortion digital filtering[J]. Chinese Journal of Mechanical Engineering, 2004, 40(3): 50-54.

[11] 郭瑜，秦树人. 旋转机械非稳定信号的伪转速跟踪阶比分析[J].振动与冲击，2004, 23(1): 61-69.

GUO Yu, QIN Shuren. Pseudo-speed tracking order analysis for non-stationary[J]. Journal of Vibration and Shock, 2004, 23(1): 61-69.

[12] CHENG Weidong, GAO R X, WANG Jinjiang. Envelope deformation in computed order tracking and error in order analysis[J]. Mechanical Systems and Signal Processing, 2014, 48(1/2): 92-102.

[13] SAAVEDRA P N,RODRIGUEZ C G. Accurate assessment of computed order tracking[J]. Shock and Vibration, 2006, 13(1): 13-21.

[15] RANDALL R B, ANTONI J. Rolling element bearing diagnostics-a tutorial[J]. Mechanical Systems and Signal Processing, 2011, 25(2): 485-520.

[16] ANTONI J, RANDALL R B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rolling machines[J]. Mechanical Systems and Signal Processing, 2006, 20(2): 308-331.

[17] 彭富强，于德介，武春燕. 基于多尺度线调频基稀疏信号分解的包络解调方法及其在齿轮故障诊断中的应用[J]. 机械工程学报, 2010, 46(12): 1-12.

PENG Fuqiang, YU Dejie, WU Chunyan. AM-FM signal extraction method by the sparse signal decomposition based on multi-scale chirplet and its application to gear fault diagnosis[J]. Journal of Mechanical Engneering, 2010, 46(12): 1-12.

[18] LIANG M, BOZCHALOOI I S. An energy operator approach to joint application of amplitude and frequencydemodulations for bearing fault detection[J]. Mechanical Systems and Signal Processing, 2010, 24(5): 1473-1494.

Fault feature extraction method for rolling bearings based on chirplet path tracing

CHENG Weidong, LIU Dongdong, ZHAO Dezun

(School of Mechanical Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044, China)

Aiming at fault diagnosis of rolling element bearings under disturbances of variable rotating speed and gear vibration noise, a fault feature extraction method for rolling bearings was proposed based on the chirplet path tracing method here. Firstly, the original vibration signals were transformed with Hilbert transformation to get envelope signals, the envelope ones were down sampled under the condition of satisfying the sampling theorem. Then, the down sampled envelope signals were used to extract the instantaneous fault characteristic frequency (IFCF) trend curve of the faulty bearing with the chirplet path tracing method. The instantaneous fault characteristic frequency (IFCF) trend curve and the rotating speed curve of the bearing were resampled with equal time intervals and the calculating instantaneous fault characteristic coefficient (CIFCC) at each time point was gained. Finally, the fault diagnosis was completed by comparing CIFCCs with the fault characteristic coefficients (FCCs) of the outer ring, inner ring and rolling element. Through processing simulated signals and test ones without filtering and order analysis, it was shown that the method can not only detect if there is any fault in rolling bearings, but also determine the fault’s location.

gear vibration noise; variable rotating speed; fault diagnosis; chirplet; calculating instantaneous fault characteristic coefficient(CIFCC)

国家自然科学基金资助项目(51275030)

2016-03-21 修改稿收到日期：2016-05-23

程卫东 男,博士，副教授，1967年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.13.024