基于直接微分法的水下结构声学快速敏感度分析

陈磊磊， 赵文畅， 陈海波， 肖琪聃

(1.信阳师范学院 土木工程学院，河南 信阳 464000； 2.中国科学技术大学 近代力学系，合肥 230026)

基于直接微分法的水下结构声学快速敏感度分析

陈磊磊1， 赵文畅2， 陈海波2， 肖琪聃1

(1.信阳师范学院 土木工程学院，河南 信阳 464000； 2.中国科学技术大学 近代力学系，合肥 230026)

在降低结构振动噪声方面，结构声学优化方法展现了很高的应用潜力，并越来越受到研究者们的重视。通过结构声学敏感度分析建立辐射声场与结构材料属性和结构形状参数的关系，结合优化算法可设计出低辐射噪声和高声隐身性能的水下航行结构。发展耦合有限元法与快速多极高阶非连续边界元法进行流固耦合问题的敏感度分析，克服传统耦合算法的计算精度低，内存占有量高，难以进行大规模实际问题的计算等问题。设计变量可选为流体密度、结构密度、泊松比、杨氏模量、壳厚度和形状参数等。针对不同设计变量，采用直接微分法分别推导出结构声学系统和辐射声功率敏感度表达式。通过带有解析解的水下点激励球壳算例验证算法的正确性与有效性，并通过简化潜艇算例展示该算法在大规模实际问题上的应用潜力。

辐射声功率；敏感度分析；耦合有限元与边界元；非连续边界元

水中航行结构振动辐射噪声不仅影响结构内部人员的身心健康，也对海底生物造成干扰。降低振动噪声和提高水下结构的声隐身性能是一项非常重要的研究课题。进行水中结构(尤其是薄壳结构)的振动响应分析，流体附加作用不可忽略，同时也增加了数值计算的难度。考虑到有限元在结构振动响应分析和边界元在无限域外声场分析时的各自优点，国内外许多学者采用耦合有限元与边界元方法(FE/BE)进行流固耦合分析[1-4]。然而现有研究大多采用传统边界元进行声场分析，计算量大，内存占有量高，难以进行大规模实际问题的数值计算。文献[5-6]使用快速多极算法(Fast Multipole Method,FMM)加速流体边界元计算，提高了流固耦合问题的计算效率，降低了内存占有量。然而这些研究大多采用常量边界元进行声场计算，为了提高计算精度，加大结构离散，导致新的计算困难产生。相对于已经被广泛使用的连续线性和二次边界元，高阶非连续边界元不仅计算精度高而且避免处理角点问题，尤其在耦合系数矩阵、湿表面面积阵及其逆矩阵的计算上，更加简单和有效[7]。本文结合高阶非连续边界元与快速多极算法形成快速多极高阶非连续边界元进行结构声学计算，提高传统耦合算法的计算精度和计算效率。另外使用单Helmholtz边界积分方程进行外声场计算时，会产生解的非唯一性问题，本文使用Burton-Miller方法克服这一问题[8]。

通过敏感度分析研究水中振动结构辐射声场与结构本身的材料属性和形状参数的关系，可指导结构材料的选取和形状设计，以降低辐射噪声和提高水下结构的声隐身性能。文献[9-10]使用快速多极边界元法进行声学敏感度分析，没有考虑声振耦合，文献[11]采用耦合FEM/BEM(Boundary Element Method)方法进行声振耦合计算，然而在进行敏感度分析时忽略了耦合作用。实际上对声振耦合方程进行敏感度分析是非常困难的，既要进行结构有限元敏感度计算，又要进行声学边界元敏感度计算，同时还需考虑耦合矩阵的敏感度结果，因此现有研究很少进行考虑声振耦合的敏感度分析。本文克服这些困难，对此进行深入研究，推导出结构声学耦合敏感度表达式，设计变量可选取为流体密度、结构密度、泊松比、杨氏模量和形状尺寸参数等。针对不同设计变量分别推导出结构振动辐射声功率敏感度表达式，进而找到目标函数与设计变量的对应关系，为基于敏感度分析的结构声学优化设计奠定基础。最后使用带有解析解的简单算法验证本文算法的正确性和有效性，使用简化潜艇模型展现本文算法在大规模实际问题中的应用潜力。

1 结构声学耦合系统

1.1 水下结构声学系统

组合水下结构振动有限元方程与流体边界元方程得到表达式

(1)

对于实际工程问题，直接求解式(1)，可得到位移响应u和声压响应p，然而计算量和内存占有量非常大，难以收敛，并且计算精度不高。为了提高耦合算法的计算效率，将式(1)中的结构振动有限元方程代入到流体边界元方程中，形成耦合边界元表达式[7]

Hp-GWCsfp=pi+GWfs

(2)

其中，

W=ω2ρfS-1CfsD-1

D=K-ω2M+iωC

(3)

观察式(2)发现存在D-1项，实际上直接求解结构矩阵的逆是非常耗时的，本文在计算式(2)右边D-1fs时，先通过求解线性系统方程Dx=fs，得到x向量即为D-1fs的结果。另外，本文使用GMRES迭代方法求解式(2)，假设第k次迭代步对应的节点声压向量为pk,在计算式(2)左边D-1Csfpk时，先计算Csfpk=b，然后通过求解线性系统方程Dx=b获得x向量以得到D-1Csfpk的结果。在每次迭代过程中该系统方程都需要被重新求解，由于D矩阵是稀疏带状的，使用稀疏直接求解器(Sparse Direct Solver)能十分有效且精确地求解这一系统方程。实际上在每次迭代计算中最耗时的是式(2)的求解，如果使用传统边界元算法进行该方程的求解，对于N自由度问题(流体边界元自由度为N)，计算复杂度为O(N2)，内存占有量也为O(N2)，这无疑是非常耗时和耗内存的，限制了该方法在大规模实际问题中的应用。本文采用宽频快速多极算法加速传统边界元算法中的矩阵向量相乘，同时避免计算流体边界元系数矩阵G与H，对于N自由度问题，计算复杂度为O(N)，内存占有量也为O(N)，降低了计算量和内存占有量，推进了耦合有限元与边界元法在大规模实际问题中的应用。

1.2 水下结构声学系统敏感度分析

在进行敏感度分析时，首先需要确定设计变量，本文针对不同设计变量，例如流体密度、结构密度、泊松比、杨氏模量、结构形状尺寸等，分别给出相应的敏感度计算表达式。在下面的计算过程中，v代表设计变量。

(1) 当选取流体密度ρf为设计变量，直接将式(2)对设计变量ρf进行微分，可得到如下敏感度表达式

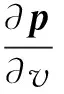
(4)

(3) 当选取结构形状参数为设计变量，直接将式(2)对设计变量进行微分，可得

(5)

a=WCsfp+Wfs

(6)

使用式(2)得到节点声压向量值p，然后利用式(4)或式(5)可以得到节点声压向量敏感度值。观察式(6)可发现存在D矩阵求逆后再求导的计算，实际上直接计算D-1已经是十分耗时的，再求导更是非常困难和耗时。为了避免直接计算D-1的导数，本文推导出如下表达式来代替D-1的导数

(7)

本文采用有限差分法来计算式(7)中的D的导数项，设定的有限差分步长为10-4。如果使用传统边界元方法进行数值计算，会形成系数矩阵G与H，采用有限差分法可以得到其敏感度结果，然而正如前文所说，该方法计算效率低，实际上对于G或H的敏感度矩阵与向量的相乘，类似于G或H与向量的相乘，可以使用快速多极算法进行加速计算，无需直接计算G、H及其敏感度矩阵，提高了计算效率，降低了内存占有量，为大规模实际耦合问题的敏感度计算及其优化分析提供了有效的数值方法。

使用边界元法可得到流体域内任一点处的声压p

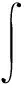
(8)

式中：G(x,y)=iρfωeikr/(4πr);F(x,y)为G(x,y)在点x处的法向导数值;y为域内计算点;S为流固耦合面;r为点x与y的距离。使用式(8)可以得到流体域内任意点处的声压值，将式(8)对设计变量进行微分，可得到流体域内任意点处的声压敏感度值。

1.3 水下结构振动辐射声功率的敏感度计算

在流体中，围绕振动结构的任意面上的辐射声功率表达式为

(9)

(10)

式中，v为流固耦合面上流体法向速度向量，与结构节点位移向量u具有如下转换关系

v=-iωS-1Cfsu

(11)

使用式(2)得到节点声压向量p，然后利用式(1)中的第一式(结构有限元方程)，得到结构节点位移响应u，最后将式(11)代入到式(10)中，即可得到流固耦合面上的结构振动辐射声功率。

将式(10)对设计变量进行微分得到如下表达式

(12)

(13)

式中:()H为向量取共轭后再转置;w1与w2表达式为

w1=iωCfsu*

(14)

耦合系数矩阵Cfs由结构形状参数决定，与流体密度、结构材料属性等参数没有关系。因此，当结构形状参数被选为设计变量时，Cfs的导数值存在，否则为0。利用式(4)或式(5)可以得到节点声压向量敏感度值，为了得到辐射声功率的敏感度值，还需计算得到节点位移的敏感度值，下面针对不同设计变量，分别推导出u的敏感度表达式。

(1) 当选取流体密度ρf为设计变量，直接将式(1)中的第一式对设计变量ρf进行微分，可得到如下敏感度表达式

(15)

(2) 当选取结构密度ρs、泊松比v、杨氏模量E、壳厚度等参数为设计变量时，得到

(16)

(3) 当选取结构形状参数为设计变量时(例如球壳半径)，得到

(17)

使用式(15)～式(17)可以得到节点位移敏感度值，然后利用式(12)即可得到辐射声功率敏感度值。

2 数值算例

2.1 数值计算离散单元

在数值计算中，先使用有限元软件ANSYS建立和离散结构模型，导出每个单元的刚度、质量矩阵，然后使用一维变带宽存储方法进行所有单元矩阵的整合，最后形成整体刚度和质量矩阵，由于结构矩阵的稀疏与对称性，只需存储整体矩阵的上三角非零元素，使用3个一维数组可有效存储整体矩阵，第一个数组存储整体矩阵上三角每行非零元素的数量，第二个数组存储上三角每行非零元素的列编号，第三个数组存储上三角每行非零元素的值。同时，采用相同网格进行结构有限元与流体边界元的计算。使用Shell281壳单元进行水下薄壳结构有限元计算，在每个节点处有3个位移自由度和3个旋转自由度；为了克服传统连续边界单元的计算精度低，角点处处理困难等问题，本文使用带有二次几何形状近似的非连续线性边界单元BE94进行流体边界元的计算，BE94单元表示使用9节点进行几何插值计算，使用内部4节点进行物理插值计算，详细的单元描述和插值过程请参考文献[7]。

2.2 水下点激励球壳算例

本节进行水下薄球壳在单点激励时的振动响应分析，球壳半径为r，坐标原点在球心处，单位幅值的点激励作用在点(r,0,0)上，详细模型图见文献[7]，流体与结构参数如表1所示。文献[7]给出了该模型振动位移响应与辐射声压的解析表达式。由于该模型沿X轴轴对称分布，流固耦合面上的振动辐射声功率可表达成

(18)

式中:θm=mπ/n;v*f(θm)=iωu*(θm)，足够大的n能产生高精度的计算结果。将上式对设计变量进行微分可得到辐射声功率敏感度的解析表达。

表1 水下球壳的材料与几何参数

在图1中，“FE88/FMBE94”表示使用Shell281单元(8节点)进行结构有限元分析，使用带有二次几何形状近似的非连续线性单元BE94进行流体边界元计算，同时使用FMM算法进行耦合边界元方程的快速求解。“FE44/FMBE41”表示使用Shell63单元(4节点)进行结构有限元分析，使用带有线性几何形状近似的非连续常量单元BE41进行流体边界元计算，同时使用FMM算法进行耦合边界元方程的快速求解。设计变量分别为流体密度和结构密度，计算频率为50 Hz,计算点分布在距离球心R=2r的圆环上，离散单元数为384。观察这两个图发现，高阶耦合单元的计算结果与解析解符合的比较好，然而低阶单元的误差比较大，验证了本文算法的高精度特点。

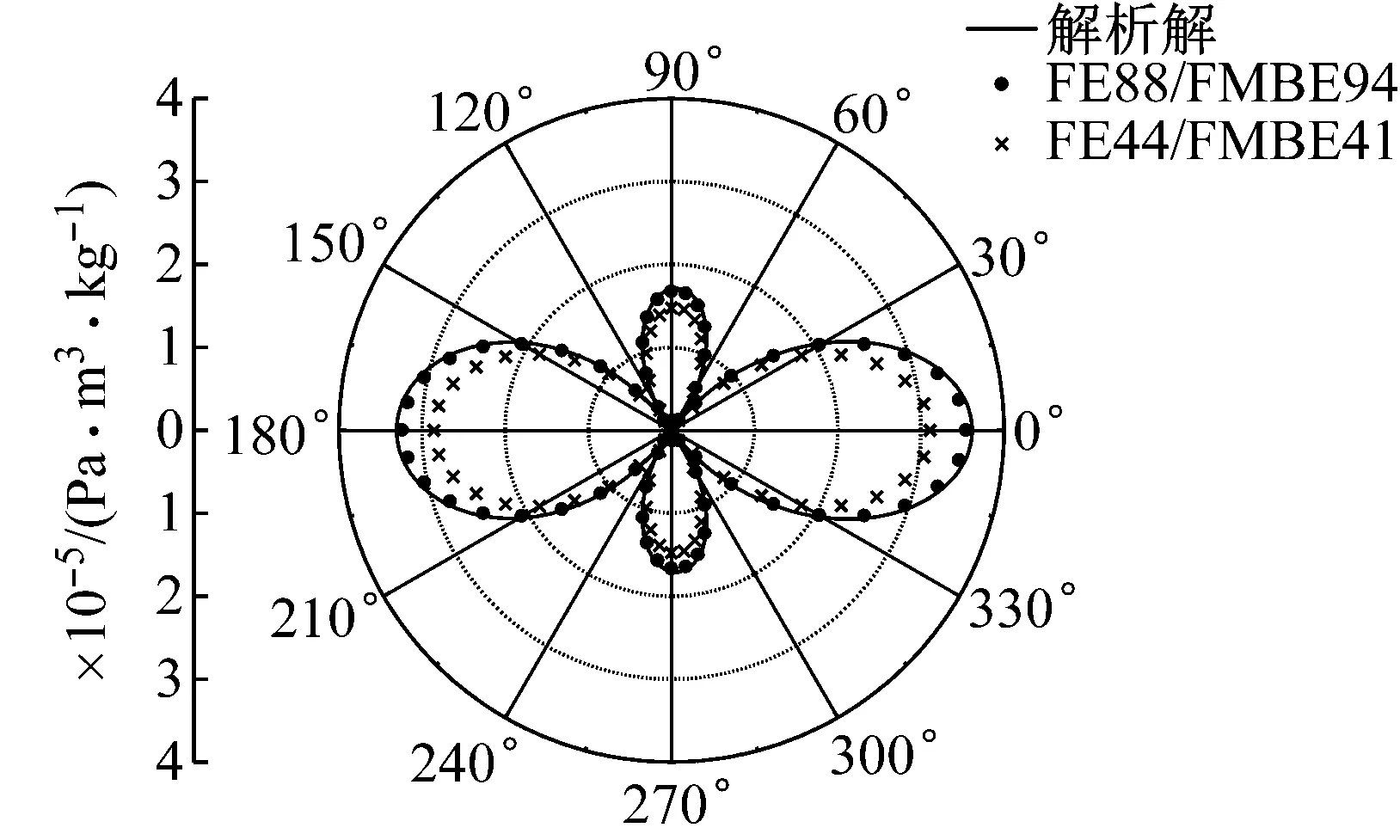
(a) 流体密度

(b) 结构密度

Fig.1 Radiated sound pressure sensitivity at distanceR=2rat 50 Hz

在图2中，后缀“BM”表示使用Burton-Miller方法进行流体边界元计算，“CBIE”表示使用传统单Helmholtz边界积分方程进行流体声场计算。解析解曲线的计算频率步长为0.01 Hz，数值解步长为2 Hz，离散单元数为864。观察该图可以发现在100 Hz以内的水下结构本征频率依次为55.9 Hz、70.5 Hz、80.6 Hz、88.4 Hz和94.8 Hz。另外，使用“CBIE”方法在148 Hz左右得到的数值结果偏离解析解，实际上是由于传统单Helmholtz边界积分方程在计算外声场问题时会产生非唯一解的问题，然而使用Burton-Miller法可以有效的解决这个问题。

图2 在点(2r,0,0)处的声压随计算频率变化图

图3呈现了流固耦合面上的辐射声功率敏感度幅值随计算频率变化关系，设计变量依次选取为流体密度、结构密度、泊松比、杨氏模量、球壳厚度和半径。观察这些图可以发现在低频处敏感度幅值比较小，在结构本征频率处迅速变化，在一些频率处急速降低(表现为近似向下垂直线)是由于敏感度值在该频率附近迅速变化并且发生算法符号的改变，例如由正变负，或由负变正。另外，在这些图中，数值解与解析解都符合的比较好，验证了本文算法的正确性和有效性。

(a) 流体密度

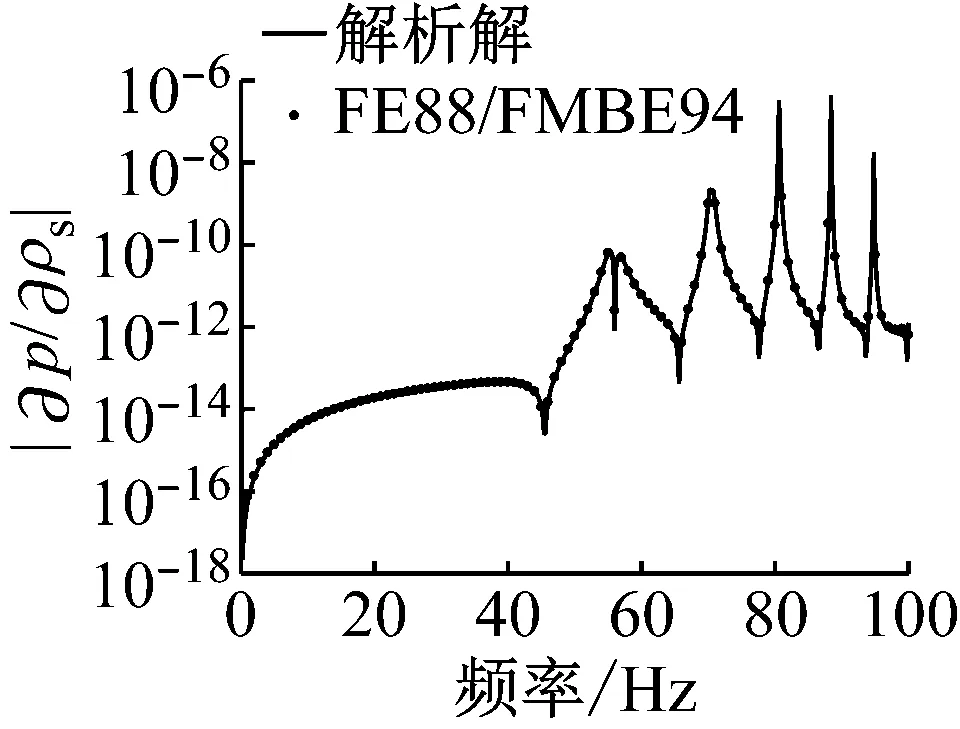
(b) 结构密度

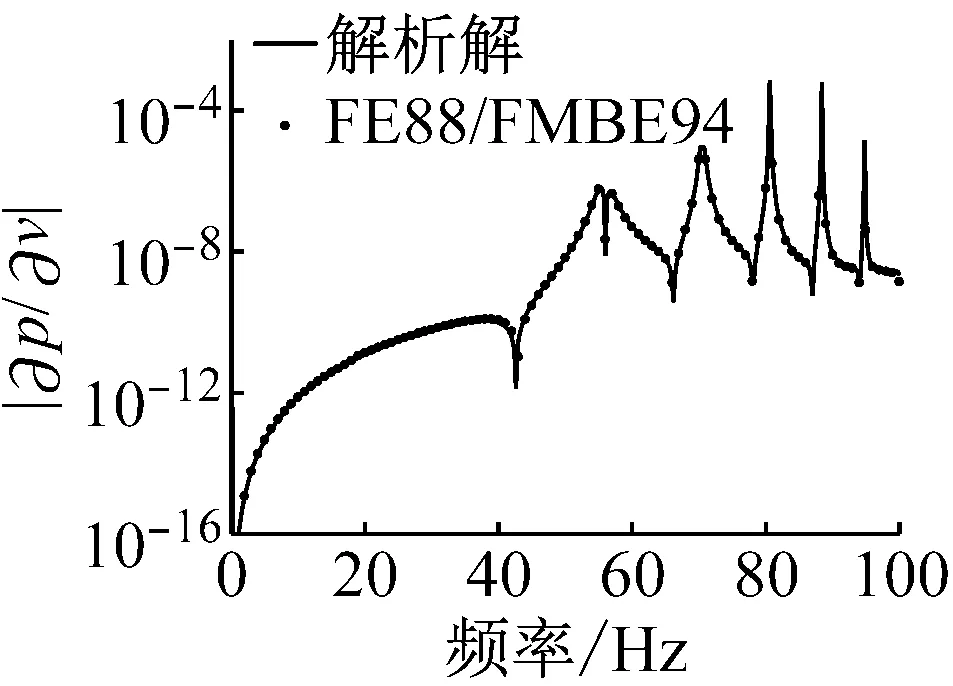
(c) 泊松比

(d) 杨氏模量

(e) 壳厚度

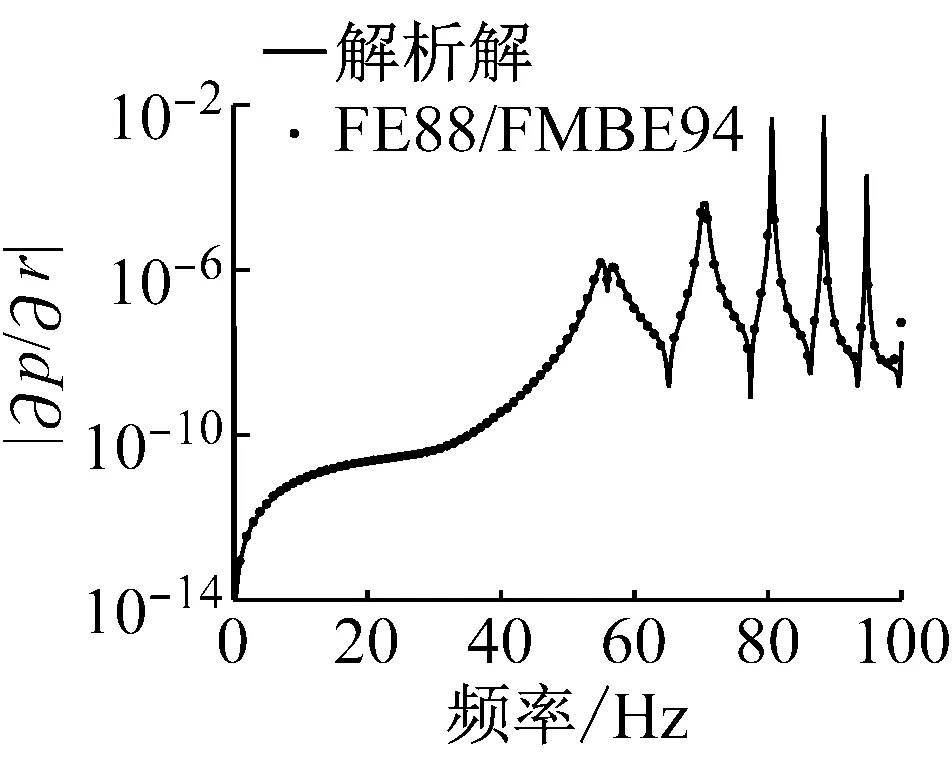
(f) 球半径

Fig.3 Amplitude of radiated sound power sensitivity on the fluid-structure interaction surface in terms of frequency

图4给出了在计算频率为50 Hz时使用传统算法与快速算法在计算流固耦合面上的辐射声功率值时所耗费时间的对比。其中“刚性解”和“加速刚性解”分别表示使用传统边界元和宽频快速多极算法加速计算刚性球模型时所需的时间(不考虑流固耦合)；“弹性解”和“加速弹性解”分别表示使用传统耦合有限元与边界元法和耦合有限元与宽频快速多极边界元算法计算弹性球模型时所需的时间。由图4可发现，网格数越多，宽频快速多极算法的加速效果越明显。另外，耦合分析比非耦合分析耗费更多时间，这是因为在耦合分析的迭代计算中，每一步都需要求解方程Dx=b，并且弹性耦合的迭代收敛次数远大于刚性分析次数。

图4 计算时间随单元数变化关系

表2给出了采用三种不同类型耦合单元在相近流体边界节点自由度下(约1 536)计算辐射声功率时的精度对比，表中的误差数据表示百分误差，选取5个频率进行数值计算。表中“FE44/FMCBE44”表示采用线性有限壳单元(Shell63)进行结构分析，线性连续边界单元进行声场分析；“FE88/FMCBE88”表示采用二次有限壳单元(Shell281)进行结构分析，二次连续边界单元进行声场分析。观察表2可以发现FE44/FMCBE44单元表现最差，FE88/FMBE94单元表现最好。另外在80 Hz本征频率处计算误差非常大，在200 Hz以外计算误差随频率迅速增加，总之耦合非连续单元表现最好。

表2 三种不同离散耦合单元计算精度对比

Tab.2 Comparison of calculation accuracy for three different types of coupled elements %

2.3 简化潜艇结构声学响应分析

简化潜艇的形状与尺寸如图5所示，分别进行在平面波作用下(沿着正X轴方向传播，幅值为1 Pa)和在模型两端的A点与B点处施加集中力F作用下(幅值为1 N)的结构声学响应分析，流体密度，结构材料属性参数和壳厚度见表1。

图5 两端分别用锥形壳和半球壳封闭的圆柱壳模型

Fig.5 An elastic cylindrical shell with a half-spherical shell and a conical shell

首先进行平面波入射时的声散射分析。图6给出了在计算点(-50,0,0)处的声压随计算频率的变化关系，“刚性解”表明不考虑流固耦合作用，仅采用FMBE94流体单元进行声学计算，得到流体域内计算点处的声压；“弹性解”是采用FE88/FMBE94耦合单元进行流固耦合计算。观察该图可以发现，刚性解与数值解的偏差随着频率增加而增大，表明进行水下薄壳结果的振动响应分析时必须考虑流体的附加作用。

图6 在计算点(-50,0,0)处的声压随频率变化图

Fig.6 Sound pressure at a computing point (-50,0,0) in terms of frequency

图7呈现了在计算点处声压敏感度幅值随频率变化关系，壳厚度选为设计变量。使用快速算法得到的计算结果与传统算法得到的计算结果吻合一致，表明快速算法的使用没有降低计算精度，保持了传统边界元方法的高计算精度优点。另外，在进行平面波作用下的结构散射声场敏感度计算时，若不考虑流固耦合，只须求解声学敏感度边界积分方程，若考虑流固耦合须求解耦合边界元敏感度方程，增加的计算困难就是耦合矩阵与结构矩阵敏感度的高效求解，尤其当高阶耦合单元被使用，更是增加了这一困难。本文使用ANSYS软件进行结构矩阵的计算，并采用有限差分法计算结构矩阵的敏感度结果。

图7 在计算点处对壳厚度的声压敏感度幅值随频率变化

Fig.7 Sound pressure sensitivity with respect to the thickness of the shell at the computing point

然后考察在集中力作用下，该模型的振动响应。图8和图9分别给出了流固耦合面上的辐射声功率和其敏感度幅值随频率变化关系，设计变量为壳厚度。同样的，刚性解与弹性解差别很大，实际上结构越薄，耦合影响就越大。

图8 流固耦合面上辐射声功率随频率变化

Fig.8 Radiated sound power on the fluid-structure interaction surface in terms of frequency

图9 流固耦合面上辐射声功率敏感度幅值随频率变化

Fig.9 Amplitude of radiated sound power sensitivity on the fluid-structure interaction surface

3 结 论

本文首先推导出用于进行流固耦合分析的耦合边界元方程和结构振动辐射声功率表达式，然后针对不同设计变量分别推导出相应的结构声学敏感度和结构振动辐射声功率敏感度表达式，通过带有解析解的点激励球壳算例验证本文算法的有效性和正确性，通过简化潜艇算例验证本文算法的应用潜力，下一步对整个算法过程与程序编写进行优化，然后对大规模实际问题进行快速敏感度分析和结构声学优化算法研究。

[1] 俞孟萨, 史小军, 陈克勤. 采用有限元和边界元方法分析弹性加肋圆柱壳的声学相似性[J]. 中国造船, 1999(3): 65-71.

YU Mengsa, SHI Xiaojun, CHEN Keqin. Study on acoustic similitude of elastic stiffened cylindrical shells by FEM and BEM[J]. Shipbuilding of China, 1999(3): 65-71.

[2] 黎胜, 赵德有.用耦合有限元/边界元方法研究加筋板的声传输[J].振动工程学报, 2001, 14(3)：364-367.

LI Sheng, ZHAO Deyou. Coupled FEM/BEM approach for analysis of sound transmission through stiffened plates[J].Journal of Vibration Engineering, 2001, 14(3)：364-367.

[3] 沈顺根, 李琪华, 王大云, 等. 加肋旋转壳结构噪声声辐射水弹性研究[J].中国造船, 1992(2): 53-62.

SHEN Shungen, LI Qihua, WANG Dayun, et al. Hydroelastic analysis of sound radiation from a stiffened shell of revolution[J]. Shipbuilding of China, 1992(2): 53-62.

[4] ZHENG H, LIU G R, TAO J S. FEM/BEM analysis of diesel piston-slap induced ship hull vibration and underwater noise[J]. Applied Acoustics, 2001, 62(4): 341-58.

[5] 陈磊磊, 陈海波,郑昌军,等.基于有限元与宽频快速多极边界元的二维流固耦合声场分析[J].工程力学, 2014, 31(8): 63-69.

CHEN Leilei, CHEN Haibo, ZHENG Changjun, et al. FEM/wideband FMBEM coupling analysis for two dimensional acoustic fluid-strucutre interaction problems[J]. Engineering Mechanics, 2014, 31(8)：63-69.

[6] JUNGE M, BRUNNER D, GAUL L. Solution of FE-BE coupled eigenvalue problems for the prediction of the vibro-acoustic behavior of shipe-like strucutres[J]. International Journal for Numerical Methods in Engineering, 2011, 87: 664-676.

[7] PETERS H, MARBURG S, KESSISSOGLOU N. Structural-acoustic coupling on non-conforming meshes with quadratic shape functions[J]. International Journal for Numerical Methods in Engineering, 2012, 91(1): 27-38.

[8] BURTON A J, MILLER G F. The application of integral equation methods to the numerical solution of some exterior boundary-value problems[J]. Proceedings of the Royal Society of London, 1971, 323: 201-210.

[9] CHEN L L, ZHENG C J, CHEN H B. A wideband FMBEM for 2D acoustic design sensitivity analysis based on direct differentiation method[J]. Computational Mechanics, 2013, 52(3): 631-648.

[10] ZHENG C J, MATSUMOTO T, TAKAHASHI T, et al. A wideband fast multipole boundary element method for three dimensional acoustic shape sensitivity analysis based on direct differentiation method[J]. Engineering Analysis with Boundary Elements, 2012, 36(3): 361-371.

[11] FRITZE D, MARBURG S, HARDTKE H J. FEM-BEM-coupling and structural-acoustic sensitivity analysis for shell geometries[J]. Computers and Structures, 2005, 82(2): 143-154.

Fast analysis for underwater structures’ acoustic sensitivity based on direct differentiation method

CHEN Leilei1, ZHAO Wenchang2, CHEN Haibo2, XIAO Qidan1

(1. School of Civil Engineering, Xinyang Normal University, Xinyang 464000, China；2. Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China)

The structural-acoustic optimization method receives more attention of designers due to its high potential in reducing structures’ vibration and noise. The structural acoustic sensitivity analysis can be used to establish relations among radiated acoustic field, structural material properties and structural shape parameters, then unwater navigating structures with lower radiated noise and higher sound-stealth performance can be designed with the optimization method. Here, the coupled algorithm was developed by combining FE and fast multi-pole higher order discontinuous BE to perform the sensitivity analysis for fluid-structure interaction problems. The developed algorithm improved the calculation accuracy and decreased the memory storage. Fluid density, structural density, Poisson’s ratio, Yong’s modulus, structural shape size and so on were taken as design variables. The sensitivity formulas for structural-acoustic system and radiated sound power with respect to different design variables were derived based on the direct differentiation method, respectively. A numerical example for an underwater spherical shell under a point excitation with an analytical solution was used to verify the validity and correctness of the developed algorithm, and an example for a simplified submarine was used to show the application potential of the developed algorithm in large scale practical problems.

radiated sound power; sensitivity analysis; coupled finite element(FE) and boundary element(BE); discontinuous boundary element(BE)

国家自然科学基金(11172291;U1504505)；河南省科技攻关项目(172102210453)；河南省高等学校重点科研项目(16B560009 ；17A560009)

2016-04-07 修改稿收到日期：2016-05-24

陈磊磊 男，博士，讲师，1986年11月生

O39

A

10.13465/j.cnki.jvs.2017.13.026