地震作用下钢筋混凝土悬臂梁抗弯性能及尺寸效应试验研究

金 浏， 苏 晓， 李 冬， 杜修力

(北京工业大学 城市与工程安全减灾省部共建教育部重点实验室， 北京 100124)

地震作用下钢筋混凝土悬臂梁抗弯性能及尺寸效应试验研究

金 浏， 苏 晓， 李 冬， 杜修力

(北京工业大学 城市与工程安全减灾省部共建教育部重点实验室， 北京 100124)

随着建筑结构尺寸的不断增大，准确的预测地震荷载作用下钢筋混凝土梁抗震性能及抗弯强度随构件尺寸增大的变化趋势对评估结构的安全性具有重要的意义。设计了剪跨比为4的5组几何相似的钢筋混凝土悬臂梁，对其在低周往复荷载作用下的抗弯性能进行试验研究，旨在探讨悬臂梁的破坏模式、延性、耗能能力，刚度退化及抗弯强度等与构件尺寸的关系。研究表明：① 不同尺寸梁的破坏模式基本相同，均在梁的固定端发生累积压缩破坏；② 随着梁尺寸增加，其延性有所增强，但耗能能力及刚度退化性能基本相同；③ 低周往复荷载作用下梁的名义抗弯强度存在明显的尺寸效应；④ Bažant尺寸效应理论能较好的描述钢筋混凝土悬臂梁在低周往复荷载作用下的尺寸效应规律。

钢筋混凝土悬臂梁； 低周往复荷载； 抗震性能； 抗弯强度； 尺寸效应

混凝土材料属于典型的准脆性非均质材料，大量试验及理论工作[1-4]证实了混凝土材料存在尺寸效应行为。钢筋混凝土构件是由混凝土及钢筋组成的复合材料，其力学性能取决于混凝土、钢筋及两者之间的相互作用[5-6]。大量试验工作，包括钢筋混凝土柱[7-8](轴压强度)、钢筋混凝土梁(抗剪强度)[9-11]及钢筋混凝土梁-柱节点等[12]的破坏性试验证实了钢筋混凝土构件层次存在尺寸效应。钢材具有良好的均质性，其表现出塑性破坏特征，因而其不存在尺寸效应。因此，钢筋混凝土构件层次尺寸效应根源于：① 组成钢筋混凝土构件的混凝土材料本身的尺寸效应；② 钢筋/混凝土之间复杂的非线性相互作用。鉴于此，国内外研究者针对钢筋/混凝土相互作用对构件层次尺寸效应的影响进行了大量的试验及理论工作。

在钢筋混凝土柱名义轴压强度尺寸效应研究方面，Bažant等探讨了长细比及箍筋约束作用对钢筋混凝土柱尺寸效应的影响规律；李冬等分析了箍筋约束作用等对柱尺寸效应的影响规律。这些研究发现，随着配箍率增大，长细比减小，钢筋混凝土柱呈现出更为“延性”的破坏特征，从而钢筋混凝土柱的尺寸效应越不明显。在钢筋混凝土梁的抗剪行为研究方面，Bažant等试验工作表明无腹筋钢筋混凝土梁抗剪强度具有明显的尺寸效应行为，而Yu等[13]研究发现有腹筋梁抗剪强度的尺寸效应行为削弱甚至丧失。这是因为无腹筋钢筋混凝土梁抗剪承载力主要由斜截面混凝土提供，其破坏特征具有明显的脆性，而对于含有横向钢筋(如箍筋)的钢筋混凝土梁来说，箍筋的存在将承担较大部分的抗剪承载力，且其显著增强了梁的延性能力，使得梁抗剪强度的尺寸效应行为减弱。以上试验均证明了构件延性越大，尺寸效应现象越不明显。

另外，也有不少学者对钢筋混凝土梁的抗弯性能进行了研究，并对抗弯强度尺寸效应进行了分析，如：Ožbolt等[14]进行了最大截面尺寸为200 mm×400 mm的两组钢筋混凝土简支梁的四点弯曲试验，发现抗弯强度不存在尺寸效应；车轶等[15-16]对横截面高度为200 mm～1 000 mm的高强混凝土简支梁进行弯曲试验，亦发现抗弯强度不存在尺寸效应；Weiss等[17-18]的试验结果均认为钢筋混凝土梁的抗弯强度不存在尺寸效应；不同的是，Rao等[19]对于钢筋混凝土简支梁的四点弯曲试验结果表明，梁的抗弯强度和塑性铰转动能力随构件尺寸增大而减小。总体来说，这些研究工作大多针对单调加载情况，钢筋混凝土梁由于纵筋的存在，在弯拉荷载作用下往往呈现出延性破坏特征，而非脆性破坏，因而其抗弯强度不存在尺寸效应，或其尺寸效应规律并不明显。

不同于单轴加载行为，在地震作用下，钢筋混凝土梁在往复加载作用下，由于低周疲劳而使得梁的破坏可能呈现出脆性破坏特征。这种由于低周疲劳而出现的脆性破坏可能使得钢筋混凝土梁的抗弯强度存在明显的尺寸效应现象。

鉴于此，本文以钢筋混凝土悬臂梁为例，设计了5组几何相似的钢筋混凝土梁构件，并进行低周往复荷载下的抗弯试验，并在试验的基础上旨在探讨：① 地震荷载作用下，钢筋混凝土梁抗震性能随结构尺寸变化的趋势；② 地震荷载作用下梁名义抗弯强度尺寸效应存在的可能性及其规律，从而能够为准确评估地震荷载作用下结构的安全性提供一定的试验支持。

1 试验概况

1.1 构件设计

试验设计按照1∶2∶3∶4∶5的几何相似比设计了5组不同尺寸的钢筋混凝土悬臂梁构件，梁的纵截面尺寸从80 mm×200 mm～400 mm×1 000 mm，梁的总高度从830 mm～4 220 mm，5组构件分别命名为CB-1，CB-2，CB-3，CB-4和CB-5，每组有2个构件，共10个构件，每组构件的详细几何参数见表1。分别对10个构件进行低周往复荷载作用下的试验研究。梁构件按照发生弯曲破坏模式进行设计，试验设计剪跨比为4。需要说明的是，试验主要进行构件层次的尺寸效应研究，不考虑材料非均质性对构件层次尺寸效应的影响。因此试验设计中，相应的材料强度，骨料直径，钢筋直径等不进行比例缩放；另外，不同尺寸构件的剪跨比、配筋形式、配箍率、混凝土强度等级等试验参数均保持不变。

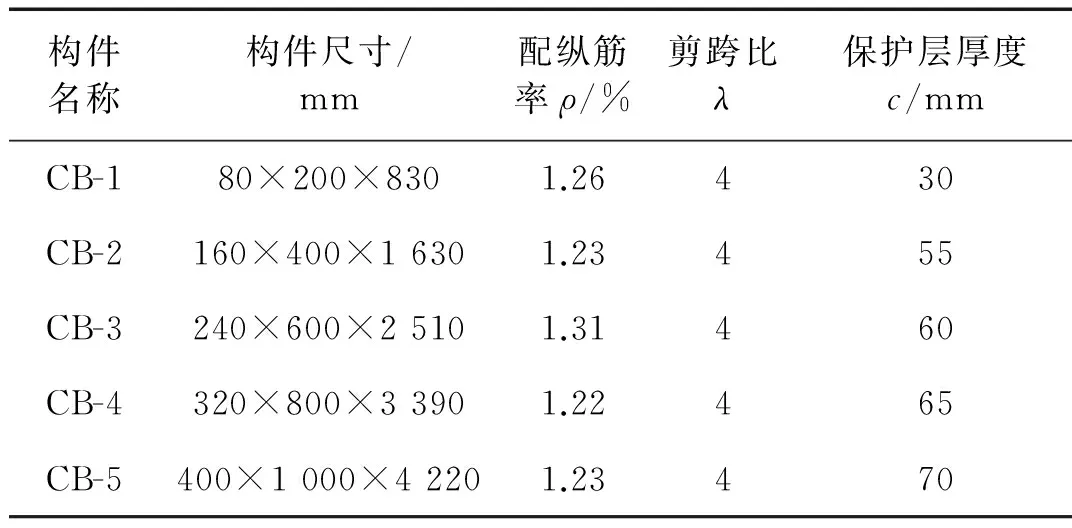
表1 构件几何参数

1.2 材料参数

所有试验构件均采用统一批次混凝土，实测立方体抗压强度平均值为42.8 MPa，劈拉强度平均值为2.3 MPa，弹性模量为27.5 GPa，立方体抗压强度和劈拉强度根据150 mm×150 mm×150 mm的混凝土立方体试块28天强度值测得。纵筋全部采用HRB335级钢筋；箍筋采用HPB235级钢筋，配箍率为0.14%，以保证构件不发生剪切破坏。钢筋参数详见表2，构件配筋图见图1。

表2 钢筋力学参数

1.3 试验加载采集方案

试验采用低周往复加载形式，结合实验室条件，利用电液伺服加载系统配合反力墙对构件进行加载。试验构件有整体浇筑的大体积混凝土底座，相当于梁的固定端，为加载方便，试验过程中将悬臂梁构件竖向锚固在实验室底板上。试验加载采集图如图2所示。

加载制度采用力和位移混合控制的方法。构件屈服前采用力控制的加载制度，每一级荷载循环一次，屈服之后的加载采用位移控制，每一级循环三次。试验需要采集主要内容包括：梁顶的水平位移值、梁顶施加荷载值。

图1 试件尺寸及配筋图

(a)(b)

图2 加载装置及测试方案

Fig.2 Loading apparatus and schematic diagram

2 试验现象和结果分析

2.1 破坏模式

以构件CB-2-ii为例，分析悬臂梁构件的裂缝发展过程和破坏模式。如图3所示，在试验加载初期，在弯矩作用下在梁的边缘产生初始细微裂缝，均匀的分布在固定端两倍梁高范围内。随着荷载增加，裂缝沿水平方继续向梁内部发展，随后由于剪力作用裂缝开始

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

斜向发展，形成若干斜裂缝，两个方向的斜裂缝相互交叉，将梁分割成若干菱形，但混土没有发生脱落，随着荷载继续增大，在循环往复作用下，梁端附近混凝土承受拉伸和压缩的反复作用，裂缝宽度也随之增大，塑性铰形成。当荷载持续增大达到极限弯曲承载力时，被拉裂的混凝土在反复拉压过程中被压碎，钢筋/混凝土之间的黏结作用逐渐减弱到消失，钢筋失去混凝土的支持很快被压屈，导致梁破坏。

低周往复荷载作用下5组悬臂梁的最终破坏形态见图4。从图4中可以看到，5组悬臂梁的破坏形态基本相同，在悬臂梁塑形铰区以上的部分，梁表面被若干裂缝分割成许多菱形，但混凝土基本没有发生脱落，固定端混凝土被压碎脱落，纵筋屈曲，最终是在梁的根部区域出现累积压缩破坏。实际上，由于悬臂梁承受低周疲劳作用而呈现出脆性破坏特征。另外，从破坏模式可以看出，钢筋/混凝土之间的相互作用对梁的抗弯强度有着不可忽略的影响，这也是在后续的数值模拟方法中必须考虑的影响因素。

5组试件的参数：

保护层厚度C=30 mm,55 mm,60 mm,65 mm,70 mm

纵筋配筋率ρ=1.26%,1.23%,1.31%,1.22%,1.23%

剪跨比λ=4

(a)80mm×200mm×830mm(b)160mm×400mm×1630mm(c)240mm×600mm×2510mm(d)320mm×800mm×3390mm(e)400mm×1000mm×4420mm

图4 10个不同尺寸钢筋混凝土悬臂梁的最终破坏模式

Fig.4 Typical failure patterns for the 10 RC cantilever beams with different structure sizes

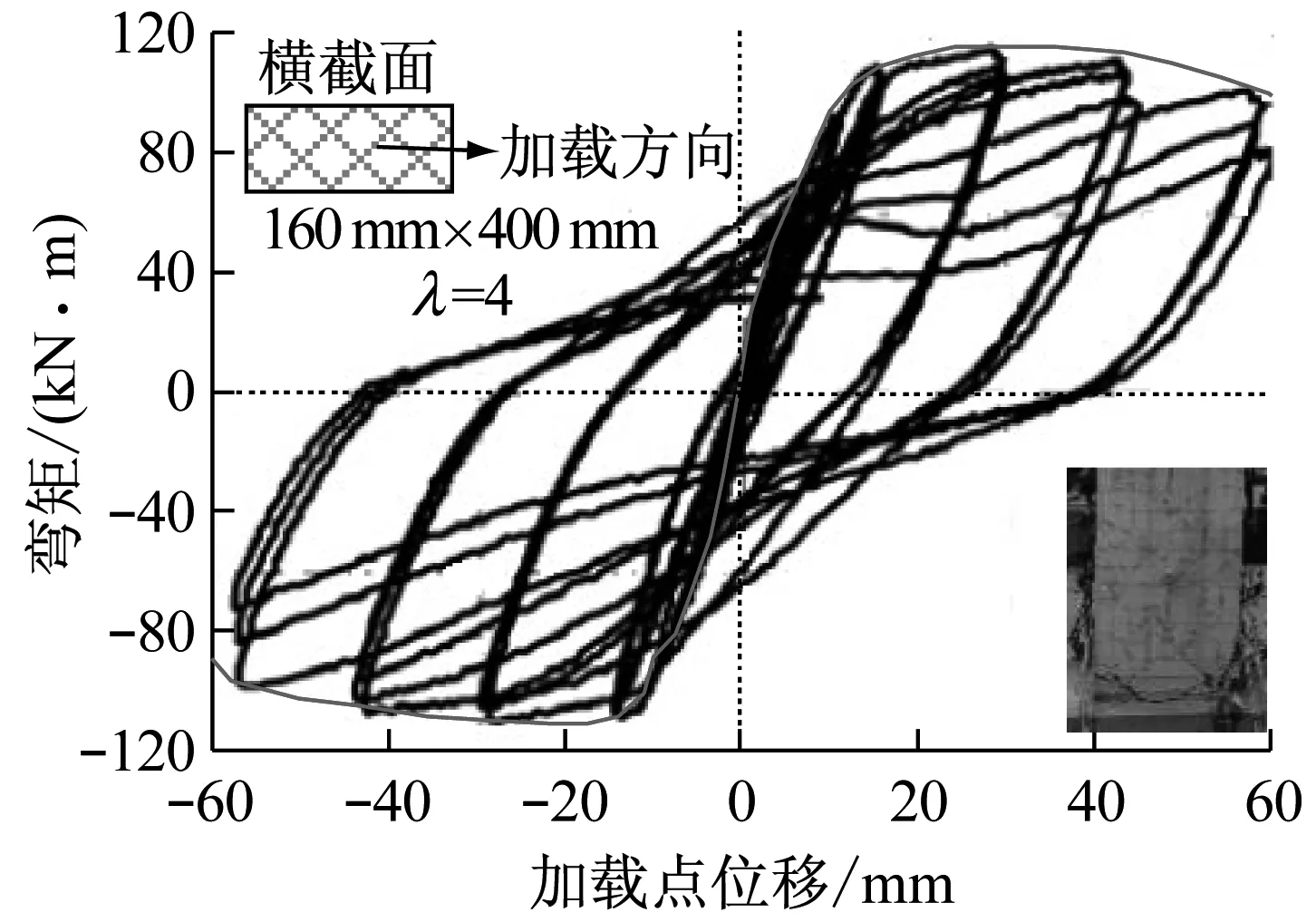
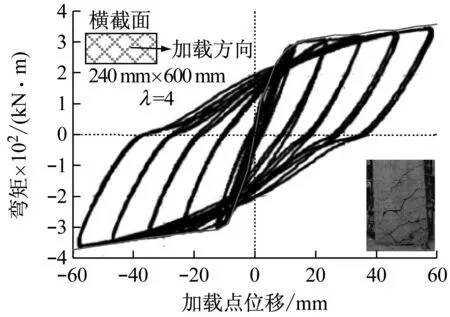
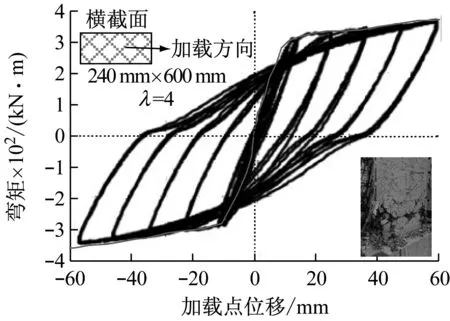
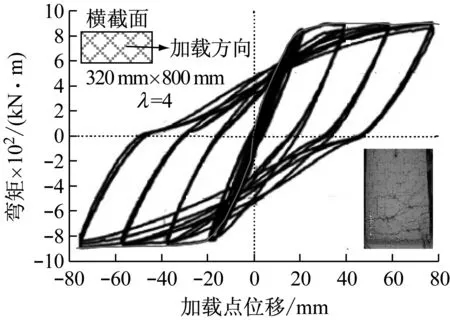
2.2 滞回曲线分析

钢筋混凝土梁在低周往复荷载作用下的滞回曲线是研究梁抗震性能的重要资料。通过滞回曲线可以分析出梁的延性、耗能能力以及刚度退化行为等重要性能。

图5给出的是10个不同尺寸悬臂梁的滞回曲线，从图5中可以看到：① 构件处于弹性阶段时，滞回环面积较小，加载曲线与卸载曲线基本上是重合的，刚度基本保持不变;② 随着荷载增加，构件底部首先出现一些水平裂缝，随后裂缝斜向发展，构件进入弹塑性阶段，滞回环面积增大，加载曲线和卸载曲线不再重合但保持平行，刚度变化不大;③ 钢筋屈服后，构件进入塑性阶段，滞回环面积显著增大，加载曲线和卸载曲线不再平行，滞回环成梭形，刚度下降明显;④ 随着荷载继续增加，悬臂梁底部受压区混凝土超过极限压应变，混凝土压碎，滞回曲线有捏拢现象，滞回曲线呈弓形，当构件超过最大承载力后，由于加载装置限制大构件该阶段的滞回曲线不理想，但从小尺寸构件的滞回曲线可以看出下降段滞回环呈反S形。

从图5可以看到，所有钢筋混凝土悬臂梁的滞回曲线都存在很明显的“捏拢”现象。滞回曲线的捏拢现象是一个很重要的特征。滞回曲线捏拢的程度与以下几个因素有关：混凝土与钢筋的黏结滑移、混凝土裂缝的开展宽度、混凝土受压过程中塑性变形的积累程度以及钢筋的应变情况等。悬臂梁在循环往复荷载作用下，裂缝不断地张开闭合，在根部混凝土出现压碎现象，梁的抗弯承载能力急速下降，抗弯刚度退化也比较严重。这是滞回曲线呈现比较明显的“捏拢”现象的原因。首先对图5进行初步的定性分析，可以看出大尺寸的构件的捏拢现象减弱，而且随着尺寸增加，骨架曲线峰值点后的水平段增长，说明大尺寸构件的延性增强。整体来看随着尺寸增加，构件滞回性能有一定的提升。

3 抗震性能分析

3.1 塑性铰转动能力

塑性铰区塑性铰转动能力是描述钢筋混凝土构件弹塑性变形能力的重要参数，由于试验中直接测量塑性铰转角比较困难，但纵向受拉钢筋屈服后试件的竖向变形主要集中在塑性铰区，塑性铰区以外区域的变形相对较小，因此采用试件挠度试验结果计算塑性铰区的塑性转角

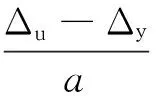
(1)

式中：θu、θy分别为极限荷载和屈服荷载时的塑性铰区两端截面的相对转角；Δu、 Δy分别为达到极限荷载和屈服荷载时所对应的梁端极限位移和屈服位移；a为加载点到固定端的距离。

从图6中可以看出构件的塑形铰转动能力规律性不强，但整体来看小尺寸构件塑性铰转动能力较低，大尺寸构件塑性铰转动能力比小尺寸构件高，这是由于小尺寸构件截面面积小，在反复受压拉过程中整个截面的混凝土很容易被压碎脱落，并很快退出工作，导致钢筋很快发生压屈破坏。而大尺寸构件主要是边缘混凝土被压碎脱落，而核心混凝土还可以提供部分抗压承载力，保护钢筋不会被压曲，从而提高了构件的塑性铰转动能力，既构件的延性随尺寸增加而有一定的增强。

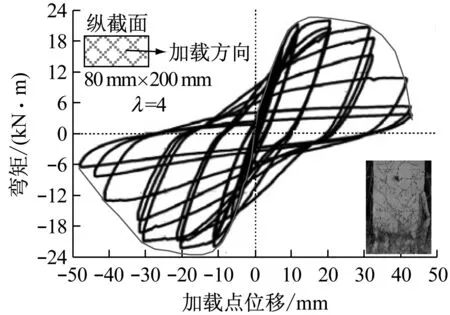
(a) CB-1-i

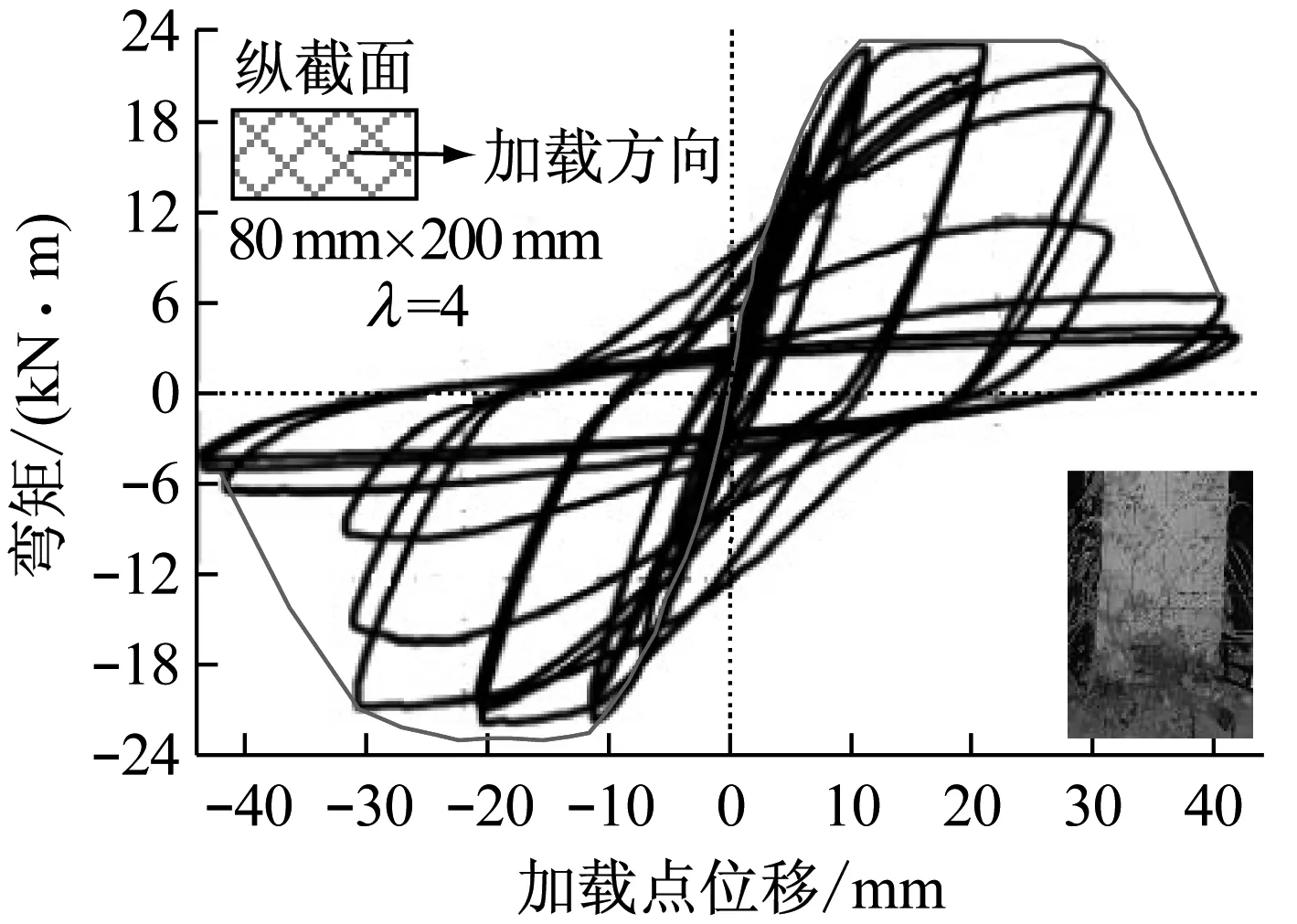
(b) CB-1-ii

(c) CB-2-i

(d) CB-2-ii

(e) CB-3-i

(f) CB-3-ii

(g) CB-4-i

(h) CB-4-ii

(a) CB-5-i

(j) CB-5-ii

图6 塑性铰转动能力随构件尺寸变化趋势

3.2 耗能能力

在低周往复荷载作用下，构件的耗能能力可以用其荷载位移滞回曲线的滞回环所包围的面积来衡量，滞回环所包围面积越大，耗散的能量就越多，构件的耗能性能就越好。图7给出了低周往复荷载作用下钢筋混凝土悬臂梁耗能能力随构件尺寸增大而变化的趋势，等效黏滞阻尼系数定义为

(2)

式中：ζi为第i次循环获得的等效黏滞阻尼；Wpl,i为第i次循环曲线包围的面积，AOAB为第i次循环对应的峰值点三角形的面积。因此，累积耗能和累积的等效黏滞阻尼分别为

(3)

(4)

图7(a)和图7(b)分别给出了累积耗能和累积等效黏滞阻尼系数随循环次数n的变化关系曲线。从图7中可以看出，随构件尺寸的增大，梁破坏时累积的耗能能量亦明显增加。另外从图7(a)可以看出，梁屈服前其耗能较弱，而屈服后的曲线斜率增大，梁的耗能迅速增加。实际上是由于梁内部裂缝迅速发展形成塑性铰而耗散了大量能量。从图7(b)可以看出，不同尺寸构件的累积等效黏滞阻尼系数基本相同，耗能能力与构件尺寸无关。

3.3 刚度退化

钢筋混凝土构件在往复荷载作用下的刚度退化特性可以用各级荷载作用下的环线刚度来描述，环线刚度定义为

(5)

式中:Ki为i级加载下的环线刚度；pi、fi分别为i级加载下加载点的峰值荷载和相应位移；+/-分别为正向加载与反向加载。

(a) 累积耗能随试件尺寸变化

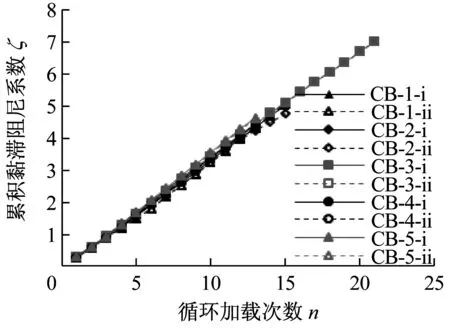
(b) 累积等效黏滞阻尼系数随试件尺寸变化

图 8为各试件归一化的环线刚度退化曲线，从图 8可以看出加载初期刚度退化比较慢，构件屈服后混凝土破坏形成塑性铰，随着混凝土被压碎脱落，截面承载力降低，刚度加速退化，当混凝土退出工作后刚度退化逐渐减缓。另外小尺寸构件的退化曲线初始斜率下降比大尺寸构件快，既刚度退化快，这是由于小尺寸构件截面上混凝土裂缝快速发展到全截面，使刚度退化趋势比大尺寸构件更快，但构件屈服以后不同尺寸构件整体刚度退化趋势基本一致。

图8 刚度退化曲线

4 抗弯强度尺寸效应分析

混凝土材料及钢筋混凝土构件产生脆性破坏时，其宏观名义强度常表现出明显的尺寸效应。一般来说，在单调加载情况下，钢筋混凝土梁的抗弯性能由于纵筋的承载作用常常表现出较强的延性，使得其不具有明显的尺寸效应，如车轶等工作。正如前文所述，在地震荷载作用下，低周往复加载使得钢筋混凝土悬臂梁由于低周疲劳而产生较为明显的脆性破坏特征。这实际上可能使得梁的抗弯强度表现出尺寸效应，下文即是对本文试验获得的抗弯强度进行分析和讨论。

4.1 名义弯曲强度随尺寸变化规律

本文采用名义弯曲强度来考察构件截面高度对受弯承载力的影响，名义强度的计算方法根据 Bažant提出的公式修改得到

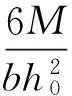
(6)

图9是名义抗弯强度随构件尺寸的变化趋势曲线。从图9中可以看到，钢筋混凝土悬臂梁的名义弯曲强度随构件尺寸(即截面高度)的增大而呈现出明显减少的趋势，展现出明显的尺寸效应规律。

图9 名义弯曲强度随尺寸变化趋势

4.2 尺寸效应分析

Bažant根据断裂力学理论提出了适合混凝土材料和构件的尺寸效应理论公式[20]

(7)

(8)

将式(8)改写为线性方程形式

Y=AX+C

(9)

首先通过对试验数据的进行回归分析后得到图10所示回归曲线，获得相应参数A和C的数值。然后，再根据Bažant尺寸效应规律分析，得到如图11所示的循环往复加载模式下钢筋混凝土悬臂梁名义强度随构件尺寸变化的双对数曲线，从图11中可以看出，本文试验获得的抗弯强度与Bažant理论曲线基本吻合，其相关系数ρXY为0.93，说明试验数据与Bažant理论曲线吻合良好，证实了钢筋混凝土悬臂梁在循环往复加载下抗弯强度存在尺寸效应行为。且Bažant尺寸效应理论能很好的描述低周往复荷载作用下钢筋混凝土梁的尺寸效应规律。

图10 对试验数据线性回归分析

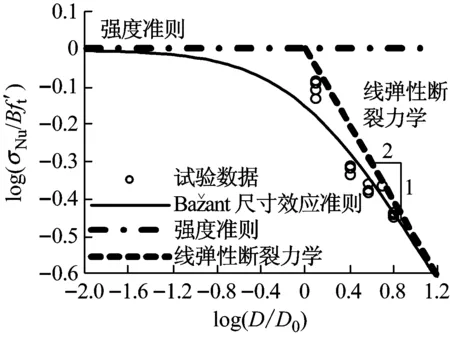
图11 名义强度随构件尺寸变化的双对数曲线

5 结 论

本文设计了5组几何相似的钢筋混凝土悬臂梁进行低周循环往复荷载作用下的抗弯试验，对梁的抗震性能以及抗弯强度随构件尺寸增大的变化趋势进行了试验分析。获得如下结论：

(1) 低周往复荷载作用下，5组构件的破坏模式相似，均是在梁端区域发生累积压缩破坏。

(2) 随着梁尺寸增加，构件的延性增强，但刚度退化和耗能能力基本保持不变。

(3) 低周往复荷载作用下钢筋混凝土梁的破坏呈现脆性破坏特征，其名义抗弯强度随构件尺寸增加而减小，存在明显的尺寸效应。

(4) Bažant提出的尺寸效应规律能较好的描述低周往复荷载作用下钢筋混凝土梁抗弯强度的尺寸效应规律。

[1] BAŽANT Z P, PLANAS J. Fracture and size effect in concrete and other quasi-brittle materials[M]. Florida: CRC Press, 1997: 7-15.

[2] HOOVER C G, BAŽANT Z P. Comprehensive concrete fracture tests: size effects of types 1 & 2, crack length effect and postpeak[J]. Engineering Fracture Mechanics, 2013, 110(2): 281-289.

[3] 王立成, 邢立坤, 宋玉普. 混凝土劈裂抗拉强度和弯曲抗压强度尺寸效应的细观数值分析[J]. 工程力学, 2014, 31(10): 69-76.

WANG Licheng, XING Likun, SONG Yupu. Mesoscale modeling on size effect of splitting tensile strength and flexural compressive strength of concrete[J]. Engineering Mechanics, 2014, 31(10): 69-76.

[4] 苏捷, 方志, 杨钻. 骨料组分和强度等级对混凝土单轴受压性能尺寸效应的影响[J]. 建筑结构学报, 2014, 35(5): 120-127.

SU Jie, FANG Zhi, YANG Zuan. Influence of aggregate mixture and strength grade on dimensional effect of concrete uniaxial compressive behavior[J]. Journal of Building Structures, 2014, 35(5): 120-127.

[5] LI Dong, JIN Liu, DU Xiuli, et al. Size effect tests of normal-strength and high-strength RC columns subjected to axial compressive loading[J]. Engineering Structures, 2016, 109: 43-60.

[6] 李冬, 金浏, 杜修力. 钢筋混凝土柱轴心受压性能及尺寸效应的细观数值研究[J]. 水利学报, 2016, 47(1): 209-218.

LI Dong, JIN Liu, DU Xiuli. Mesoscopic simulation of the mechanical properties and the size effect of reinforced concrete column subjected to axial compressive loading[J]. Journal of Hydraulic Engineering, 2016, 47(1): 209-218.

[7] BAŽANT Z P, KWON Y W. Failure of slender and stocky reinforced concrete columns: tests of size effect[J]. Materials and Structures, 1994, 27(2):79-90.

[8] SENER S, BARR B I G, ABUSIAF H F. Size effect in axially loaded reinforced concrete columns[J]. ASCE Journal of Structural Engineering, 2004, 130(4): 662-670.

[9] BAŽANT Z P, KIM J K. Size effect in shear failure of longitudinally reinforced beams[J]. ACI Journal Proceedings, 1984, 81(5): 456-468.

[10] ZARARIS P D, PAPADAKIS G C. Diagonal shear failure and size effect in RC beams without web reinforcement[J]. Journal of Structural Engineering, 2001, 127(7): 733-742.

[11] SYROKA-KOROL E, TEJCHMAN J. Experimental investigations of size effect in reinforced concrete beams failing by shear[J]. Engineering Structures, 2014, 58(7): 63-78.

[12] BARBHUIYA S, CHOUDHURY A M. A study on the size effect of RC beam-column connections under cyclic loading[J]. Engineering Structures, 2015, 95:1-7.

[13] YU Q, BAŽANT Z P. Can stirrups suppress size effect on shear strength of RC beams?[J]. ASCE Journal Structural Engineering, 2011, 137(5): 607-617.

[14] OŽBOLT J, METROVIC D, LI Y J, et al. Compression failure of beams made of different concrete types and sizes[J]. ASCE Journal of Structural Engineering, 2000, 126(2): 200-209.

[15] 车轶, 郑新丰, 王金金, 等. 单调荷载作用下高强混凝土梁受弯性能尺寸效应研究[J]. 建筑结构学报, 2012, 33(6): 96-102.

CHE Yi, ZHENG Xinfeng, WANG Jinjin, et al. Size effect on flexural behavior of reinforced high-strength concrete beams subjected to monotonic loading[J]. Journal of Building Structures, 2012, 33(6): 96-102.

[16] 车轶, 王金金, 郑新丰,等. 反复荷载作用下高强混凝土梁受弯性能尺寸效应试验研究[J]. 建筑结构学报, 2013, 34(8): 100-106.

CHE Yi, WANG Jinjin, ZHENG Xinfeng, et al. Experimental study on size effect of flexural behavior of reinforced high-strength concrete beams subjected to cyclic loading[J]. Journal of Building Structures, 2013, 34(8): 100-106.

[17] WEISS W J, GULAR K, SHAH S P, Localization and size-dependent response of reinforced concrete beams[J]. ACI Structural Journal, 2001, 98 (5): 686-695.

[18] CARPINTERI A, CORRADO M, PAGGI M, et al. New model for the analysis of size-scale effects on the ductility of reinforced concrete elements in bending[J]. ASCE Journal of Engineering Mechanics, 2009, 135(3): 221-229.

[19] RAO G A, VIJAYANAND I, ELIGEHAUSEN R. Studies on ductility and evaluation of minimum flexural reinforce-ment in RC beams[J]. Materials and Structures, 2008, 41 (4): 759-771.

[20] BAŽANT Z P. Size effect in blunt fracture: concrete, rock, metal[J]. ASCE Journal of Engineering Mechanics, 1984, 110(4): 518-535.

Tests for flexural behavior and size effects of RC cantilever beams subjected to seismic loads

JIN Liu, SU Xiao, LI Dong, DU Xiuli

(Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education Beijing University of Technology, Beijing 100124, China)

With increase in structures’ sizes, correctly predicting the varying trend of aseismic performance and anti-bending strength of reinforced concrete (RC) cantilever beams under seismic loads is of great importance to assess the safety of RC frames. Here, five groups of RC cantilever beams with geometric similarity and a shear span ratio of 4 were designed and tested under low cyclic loading. The relationships between beams’ sizes and their mechanical behaviors including failure pattern, ductility, energy-dissipating capacity, stiffness degradation and bending-bearing capacity were explored. The results indicated that ① the failure patterns of all the tested RC beams with different structural sizes are similar, all the beams damage at the fixed end due to cumulative compressions; ② with increase in beams’ sizes, their ductility increases, but their energy-dissipating capacity and stiffness degradation do not change; ③ there are obvious size effects for the nominal anti-bending strength of these RC beams under low cyclic loading; ④ the size effects of RC cantilever beams under cyclic loading can be described well using Bažant size effect theory.

reinforced concrete (RC) cantilever beam; low cyclic loading; seismic performance; flexural-tensile strength; size effect

国家自然科学基金创新研究群体(51421005)

2016-01-13 修改稿收到日期：2016-04-28

金浏 男, 博士， 教授，1985年生

杜修力 男, 博士，教授, 博士生导师，1962年生

TU528

A

10.13465/j.cnki.jvs.2017.13.003