模态参数自动识别的虚假模态剔除方法综述

宋明亮， 苏 亮， 董石麟， 罗尧治

(浙江大学 建筑工程学院， 杭州 310058)

模态参数自动识别的虚假模态剔除方法综述

宋明亮， 苏 亮， 董石麟， 罗尧治

(浙江大学 建筑工程学院， 杭州 310058)

模态参数自动识别技术的关键在于对真实模态和虚假模态进行自动甄别。对模态参数识别方法中自动剔除虚假模态的方法进行了综述。围绕如何自动剔除虚假模态，将现有模态参数自动识别方法分为三类：基于智能算法的稳定图自动分析方法、基于指标阈值的真假模态自动区分方法、基于改进识别算法获得清晰稳定图的自动分析技术。对以上三类方法的原理进行了详细的介绍，提出了各自的特点、存在的问题以及将来的研究方向。结合实测加速度数据，采用具有代表性的自动识别方法对一钢筋混凝土结构建筑进行虚假模态的自动剔除，并对不同方法的识别结果进行了比较。

模态参数； 自动识别； 指标； 稳定图； 虚假模态； 模糊聚类

结构模态参数自动识别是运营模态分析(Operational Modal Analysis, OMA)的关键步骤，也是结构健康监测的重要内容。模态参数自动识别是指，在某种参数识别方法的基础上，使用可以自动运行的程序，一旦程序运行，不再需要任何人为干扰，即可获得模态参数。在程序运行之前往往需要预先设定相应参数或阈值，剔除虚假模态。自动识别的关键步骤是自动区分真实模态与虚假模态。长期以来，这一过程主要是通过建立稳定图来人为选择真实模态。稳定图[1]的具体做法是假定不同的模型阶次，采用模态识别方法分别识别各不同阶次的模型的模态参数，将所有识别的结果以点的形式绘制在二维坐标图上。其中，横坐标表示固有频率，纵坐标表示模型的阶次。这些点包含了固有频率、模态振型和阻尼比，满足稳定条件的点被称为稳定点，且只有这些点才能被显示在稳定图上。另一方面，如果随着模型阶次的改变，这些频率、模态振型、阻尼比一致的极点若持续存在，认为这些点极有可能代表物理模态。然而，在实际工程中，由于数据量大，噪声干扰等原因，稳定图上的信息常常杂乱无章，这使得从稳定图上选择真实模态变得非常困难。一方面，人为分析复杂的稳定图，耗费的时间之长严重阻碍了对运营结构模态进行实时监测分析。另一方面，近年来，由于结构监测应用日益普遍，更多的非专业人士投入了这项工作中，使得人为主观分析稳定图的结果并不稳定可靠，即使是同样的数据应用同样的方法，获得的模态参数也可能不同。

基于以上原因，模态参数自动识别尤其是虚假模态的自动剔除技术的研究成为模态分析领域的研究热点。在最近二十年，国外学者对自动识别技术的研究较多，而国内关于这方面的研究很少。基于此，本文对结构模态参数自动识别研究领域的主要方法进行了综述。在综述过程中，主要阐述自动剔除虚假模态的过程，而不重点讨论参数识别的方法。根据这一原则，将自动识别方法分成了三类，并具体针对这些方法如何自动剔除虚假模态进行了详细的介绍。并对其特点、存在的问题以及将来的研究方向进行探讨。这三类方法分别是：基于智能算法的稳定图自动分析方法、基于指标阈值的真假模态自动区分方法和基于改进识别算法获得清晰稳定图的自动分析方法。使用混凝土结构建筑的实测数据，应用具有代表性的自动识别方法进行了模态参数的识别。最后对工程结构模态参数自动识别存在的问题以及研究方向进行了讨论。

1 基于智能算法的稳定图自动分析方法

模态参数自动识别的智能算法主要指模糊聚类技术[2]。模糊聚类技术用于对研究对象进行分类，分类依据是这些对象所包含的某些特性。分类的结果应满足同一类对象具有较高的共性，而不同类对象之间具有相异的特性。在分析稳定图时，聚类的作用是将代表同一物理模态的估计极点划分到一个聚类中。最常用的聚类方法分为两类：分层聚类和非分层聚类。分层聚类法类似于构造一个分层的树状结构，如图1所示。起初，每一个对象都被看成是单独的聚类。然后，将其中最近的两个聚类合并到一个新的聚类中。重复进行这样的合并过程，最终即可将所有对象分类到大的聚类中。分层聚类技术的优点是有充分根据地选择最终的聚类数目。而它的缺点是需要确定分层树截断规则。非分层聚类的做法是：先选择一组初始聚类中心，按照预先设定好的距离阈值将所有研究对象分类到这些聚类中心。再使用迭代算法将所有距离总和最小化，得到最终的聚类结果。非分层聚类方法的缺点是需要预先设定聚类数目和初始聚类中心。由此，可将基于模糊聚类的稳定图自动分析方法分为两类：基于分层聚类的稳定图自动分析方法、基于非分层聚类的稳定图自动分析方法。

1.1 基于分层聚类的稳定图自动分析方法

基于分层聚类的自动识别方法，先结合某种距离计算公式，采用直接聚类法，将稳定图上的极点分为N

图1 分层聚类示意图

类，然后根据每个聚类内部包含的极点个数，选择大于设定的阈值的聚类作为真实模态的代表聚类。最后再从中选出最优极点，作为真实模态的估计。该类方法的关键是如何建立分层聚类的距离计算公式与聚类截断准则。分层聚类的自动识别又可分为三类：使用分层聚类的方法、使用真假模态判别指标结合分层聚类的方法、使用其他智能算法结合分层聚类的方法。

在直接使用分层聚类进行自动识别方面，Magalhaes等[3]基于分层聚类技术对协方差驱动随机子空间法(Covariance Driven Stochastic Subspace Identification, Cov-SSI)识别得到的稳定图自动分析。使用了基于固有频率和模态置信准则(Modal Assurance Criteria, MAC)的极点距离计算准则di-j

(1)

当距离di-j足够小时，认为第i和第j个模态频率及振型相近，这两点可能代表同一阶物理模态，可归入同一聚类。但对于不同的测试条件需要人为设定不同的距离阈值。而在聚类树截断准则方面，通过在每个聚类内部，设定任意两点之间的最小距离的上限来终止分层聚类，其建议的值为0.02，如果噪声水平较高的话，还可以更高。孙鑫晖等[4]采用p-LSCF(poly-Least Squares Complex Frequency Domain Method)结合分层聚类法进行自动识别，并基于频率、阻尼比、模态参与因子值提出模糊相似系数rij对极点进行聚类，并通过设定阈值确定聚类的数目，建议其阈值取为0.9。最后统计每个聚类中包含极点数，如果该聚类中包含的极点数大于设定的阈值，则认为该聚类代表真实模态。

(2)

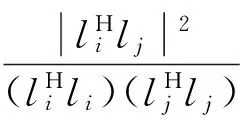
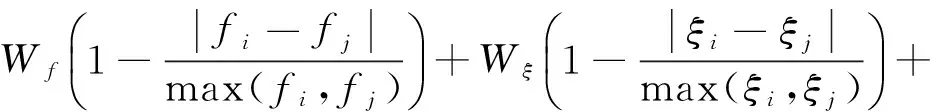
(3)

≤τ

(4)

(5)

在使用结合真假模态判别指标与分层聚类方面，Bakir[7]首先提出先使用真实极点判断指标来剔除虚假模态，然后直接使用分层聚类得到真实模态的代表聚类。其剔除虚假模态的指标是“模态相位共线性”[8](Modal Phase Collinearity, MPC)。建议MPC的阈值可取为70%。在分层聚类中，使用的距离指标为

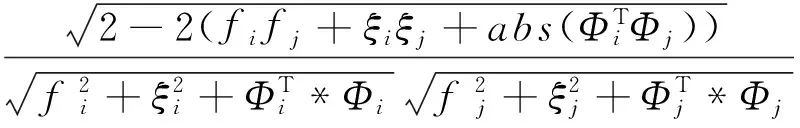
(6)

但是并未给出该指标的阈值0.1是如何确定的，同样具有一定的主观性。之后，汤宝平等[9]提出基于谱系聚类和随机子空间法的自动识别方法。先使用模态相似指数结合模态能量剔除虚假模态，后提出考虑模态能量的距离计算公式进行分层聚类。首先针对用不同方法计算得到的模态计算相似指数rm

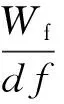
(7)

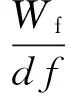
(8)

(9)

然后，对剩余极点分层聚类，聚类距离公式为

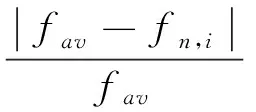
(10)

式中：fav为假定的m个阶数下求得的同一阶频率的平均值；同理，φav为平均模态向量。聚类的距离阈值设定为0.02且代表真实模态的聚类包含的元素个数需大于假定最高阶次的三分之一。

在结合其他智能算法进行分层聚类方面，Goethals等[12]提出基于分层聚类技术自动分析稳定图的方法，并使用最小二乘支持向量机自学习技术自动调整程序所需要设定的阈值和参数。一旦最小二乘支持向量机得到训练，程序可以完全自动运行。其距离计算公式基于频率和阻尼

dist(pi1,j1,pi2,j2)=

(11)

式中，δf、δd是需要人为设定的表征频率和阻尼远近的指标，而聚类截断方法通过使用最小二乘支持向量机进行训练。Rainieri等[13]则提出将分层包含元素个数阈值Nmax,cl设定为分层聚类树状图尺寸大小的函数，因而可以自动被设定，并得到聚类元素个数大于Nmax,cl的聚类，并作为真实模态的候选模态。此外，Ubertini等[14-15]认为，使用聚类算法进行模态参数自动识别可能会出现将弱激励的物理模态识别为虚假模态。因此在Hong等[16]的基础上提出了一种新的方法，该方法融合了SSI(Stochastic Subspace Identification)设定不同的i和n的识别结果。剔除不符合频率、阻尼比、MAC值稳定条件的极点后，对所有的剩余极点进行聚类，其聚类的距离准则为

(12)

最后，求出融合后的聚类中极点参数的均值以及95%的置信区间作为最终结果。

1.2 基于非分层聚类的稳定图自动分析方法

基于非分层聚类的稳定图自动分析方法主要是通过设定初始聚类中心和初始聚类数目，使用FCM聚类或者K-means聚类法通过优化目标函数自动搜索迭代计算出代表真实模态的聚类，从而自动识别出结构的真实模态参数。其大致可以分为三类：① 直接利用FCM(Fuzzy C-means)模糊聚类的方法；② 先使用真假模态判别指标剔除一部分虚假模态再使用模糊聚类的方法；③ 使用一些辅助程序结合模糊聚类的方法。

在直接使用FCM模糊聚类自动识别方法方面，姜金辉等[17]曾提出在正交多项式拟合和多参考点最小二乘复频域识别方法中引入FCM聚类，进行真实极点的自动选取。① 用正交多项式拟合法或者多参考点最小二乘复频域识别方法得到系统极点；② 设定模糊聚类参数，如聚类中心个数c，初始模糊分类矩阵U等，进行迭代，获得c个聚类中心；③ 找出每个聚类中距离聚类中心最近的极点作为该阶模态的最佳极点。该方法的关键是如何选择聚类中心个数c的值，以及模糊分类矩阵的初始化等等，而文中并未给出具体方法。

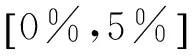
其中,

(13)

(14)

(15)

(16)

(17)

表1 8个软指标

表2 3个硬指标

MPC即如前所述，MPD、MTN(Modal Transfer Norm)计算如下

(18)

(19)

(20)

(21)

式中，MOB(Mobility of Mode)为模态迁移率。最后，用K-means聚类法在稳定图上对满足上述指标的剩余极点进行聚类,并对聚类后的每个聚类，应用式(22)计算极点之间的距离。

φj,φl)

(22)

合并距离最近的聚类，合并之后计算类内元素的平均距离，重复上述过程直到类内平均距离大于某个阈值。

在使用其他辅助程序结合模糊聚类的方法方面，Scionti等[22]提出基于模糊聚类技术和遗传算法的稳定图自动分析方法。其具体过程如下：① 将识别结果表示在“频率-阻尼比”稳定图上；② 使用遗传算法对FCM模糊聚类的初始聚类中心进行初始化；③ 进行FCM聚类；④ 计算各聚类包含的元素到该聚类中心的距离均值； ⑤ 对于每个聚类，以聚类中心为圆心，以距离的均值为半径画圆；⑥ 剔除半径远大于其他聚类的聚类；⑦ 从剩余聚类中选择代表极点，作为该阶模态参数。与此类似，Liu等[23]提出建立一种新的稳定图，以频率为横坐标，MAC值为纵坐标，并使用模糊核聚类法[24]、比较圆法在稳定图中自动识别物理模态。其中，模糊核聚类算法可适合任意形状分布样本的优点，修正了模糊聚类仅适应于球类样本的缺点。具体过程如下：① 假定一个聚类数目c，通过迭代将稳定图上的点分为c个聚类；② 计算每个聚类内包含的点到其聚类中心距离的均值，并以此为半径，聚类中心为圆心，画出比较圆；③ 将半径大的聚类作为虚假模态剔除；④ 找出每个聚类的聚类中心(通过聚类算法本身可以获得)，并找出稳定图上每个聚类内到聚类中心最近的点；⑤ 将找到的这些到聚类中心最近的点作为该阶模态的代表，即最终的识别结果。

2 基于指标阈值的真假模态自动区分方法

早期的基于真假模态判别指标的自动识别方法，主要使用了“极-零相消对”、 以及基于平衡降阶理论[25]的指标等。之后，逐渐有更多学者使用MAC值、一致模态因子[26](Consistent Mode Indicator, CMI)等作为剔除虚假模态的指标。

(1) 模态截断指标ζ1，即要验证某阶模态是否为真实模态，就将该阶模态从模态描述的模型中剔除，然后计算对于整个系统的影响。这个影响用H2和H∞范数表示。

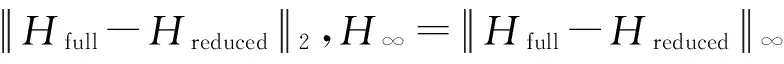
(23)

Hfull(z)-Hreduced(z)=Hi(z)=

(24)

(25)

(26)

式中,可控格拉姆矩阵Pi可以由李雅谱诺夫方程求解。最后将各阶模态计算得到的H2和H∞范数归一化得到ζ1。

(2)重要性系数ζ2，由系统平衡描述和模态描述之间的关系计算。它们之间的关系可用相似转换矩阵描述

Λ=TAbT-1Bm=TBbCm=CbT-1Dm=Db

(27)

(28)

(3) 极零相消对重要性系数ζ3。由于弱激励以及低阻尼情况下，一些真实模态极点常伴随零点存在，因而实际过程中不采用这种方法来区分虚假模态。分别将每个极点移动至与之最靠近的零点，然后计算H2和H∞范数来计算这种移动对于模型整体的影响，归一化得到ζ3。

(4) Cross Correlations重要性指标。即从可获得的观测值中构建l个MISO(Multiple-Input Single-Output)模型，并通过在复数域内计算标准欧氏距离来的方法比较这种方法获得的l个极点和完整MIMO(Multiple-Input Multiple-Output)模型获得的l个极点的差异大小。在验证上述重要性系数时，发现0.5以下不一定代表该阶模态不重要。因为重要性系数的绝对值本身意义很小。在实际应用中，可计算各重要性指标并求和再排序，确定最终真实模态的方法是查看重要性指标排序是否有突变。或者，根据感兴趣的模态阶数，直接取重要性总和排名前几的模态。文中应用实例表明，该法由于无法识别弱激励模态而会遗漏模态，且该方法只适用于子空间识别方法。

与Goethals等相同，Deraemaeker等[29]在稳定图中引入模态传递范数[30]。通过计算剔除某阶模态后所产生的影响大小，间接反映该阶模态是否为真实模态。与前者不同的是，Deraemaeker等只将具有高模态传递范数值的极点保留在传统稳定图中，因而提高了稳定图的清晰程度，促进了运营模态的自动分析。

另一方面，Lanslots等[31-33]对自动识别的可行性进行了论证，提出一些稳定点或真实模态极点应遵循的指标如：① 模态振型复杂性，计算模态具有很高的复杂性[34]；② 施加特定激励，用SIMO (Single-Input Multiple-Output)或者SISO (Single-Input Single-Output)模型识别方法验证待鉴别的极点是否依然会被识别出[35]；③ 一致模态因子CMI；④ 结合频域极大似然估计法剔除虚假极点的验证准则，如极点估计的不确定性、极-零对、极-零相关系数等;⑤ 与子空间法相关的一些指标[36],如模型缩聚后求影响的范数、平衡模态理论的状态能量解释、被动极-零相消等。Lanslots等介绍了LMS公司开发的LMS Cada-X软件自动识别真实模态的方法：用PolyMAX识别模态参数，并使用基于人工选择极点的规则自动进行极点选取，最后用以下指标进行了验证，并与4位专家、4位新手的识别结果进行了对比。将识别得到的真实模态极点合成频响函数，并将之与实测响应得到的频响函数进行对比，并用CMIF(Complex Mode Indicator Function)指标、MPC、MPD进行验证。发现CMIF验证情况较好，而MPC、MPD情况并不好，有很多真实模态的MPC在80%左右，MPD在30%左右。

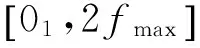
(29)

此外，Liu等[45-47]提出模态参数的优化和盲辨识法剔除虚假模态，实现OMA的自动分析。采用了三种指标来自动剔除虚假模态：① 若两个相近极点的MAC>0.9，那么可以将模态振型能量小的那个极点作为虚假极点剔除；② 剔除阻尼比大于10%的极点；③ 设MIIr为r阶模态的平均振动能量与所有极点中的最大模态能量的比值，剔除MIIr小于阈值0.001的极点极。以下是MIIr的推导

输入i和输出j之间的频响函数

(30)

对于任一阶模态，质量归一化，mr=1,p为输出数目，忽略输入位置的影响，得

(31)

(32)

MIIr=Er/Emax

(33)

式中：Er为r阶模态的平均振动能量；Emax为所有极点中的最大模态能量。

3 基于改进识别算法获得清晰稳定图的自动分析方法

本节突出介绍在自动分析稳定图时提出的一些新的思路，对其使用的方法做简要的介绍。这些方法或者是在原有方法上提出新的自动分析稳定图方法，或者是提出全新的参数识别方法。

在使用新方法方面，Verboven等[55]使用(Frequency-domain Linear Least-squares, LSCF)进行自动识别，该方法可以快速建立稳定图，并将LSCF得到的稳定图表示在s域上，可以明显地发现真实模态和虚假模态的不同，真实模态的聚类十分明显，这表明可用聚类技术进行自动识别，使用了分层聚类技术进一步进行了自动识别。Poncelet等[56]提出基于二阶盲辨识(Second-Order Blind Identification, SOBI)的自动识别方法，通过拟合实测响应的方法求解频率和阻尼比，然后由得到的各阶频率、阻尼比拟合的响应与实测响应的误差，找到误差较大的模态，认为是虚假模态。Phillips等[57-58]提出满足UMPA(Unified Matrix Polynomial Algorithm)结构的所有算法的自动识别过程：① 使用任一种UMPA算法，绘制稳定图；② 寻找聚集的模态向量；③ 求解极点表面密度聚类；④ 形成归一化的极点加权向量；⑤ 计算归一化的极点加权向量的Auto-MAC值；⑥ 剔除Auto-MAC值小于阈值0.8的加权极点向量；⑦ 识别并保留一致极点加权向量聚类；⑧ 评估极点聚类；⑨ 完成每个极点聚类的数值评估，包括均值与方差；⑩ 评估识别结果的质量。这篇文章重点研究了基于UMPA的自动识别方法的总体流程，但是没有针对虚假模态如何自动剔除作出深入研究。

4 算 例

为了比较自动识别算法与人工识别算法识别结果，进一步理解自动剔除虚假模态的过程，自主编制了基于SSI模糊聚类和FDD-MAC两种自动识别的Matlab程序，并以如图2所示的加拿大一所运营中的钢筋混凝土结构大楼[59](Heritage Court Tower, HCT)为研究对象，结合Felber[60]研究团队采集的环境激励振动加速度数据识别该建筑的模态参数，最后与现有人工识别结果进行比较。

所采用的测试数据共有为4个分布，其中第1分布包含6个通道，其他分布各有8个通道，每个通道包含13 108个加速度数据，采样频率为40 Hz。图3为第1分布的前3个通道的加速度。

图2 HTC示意图

分别使用随机子空间法结合FCM聚类、频域分解法结合MAC指标两种方法识别HTC前6阶模态，并与人工识别结果进行对比。如图4所示，为SSI自动识别算法所求得的稳定图。其中“☆”表示频率、阻尼、振型都稳定的点，“○”代表频率，阻尼稳定点，代表仅有频率稳定的点。

在此基础上采用模糊FCM聚类技术，筛选出频率小于10 Hz的前6个聚类，即包含聚类数目最多的前6个聚类，再从各聚类中选择代表模态，即可自动从稳定图上获得真实模态。如图5所示，代表真实模态的聚类包含的元素个数要远远多于虚假模态。

(a)

(b)

(c)

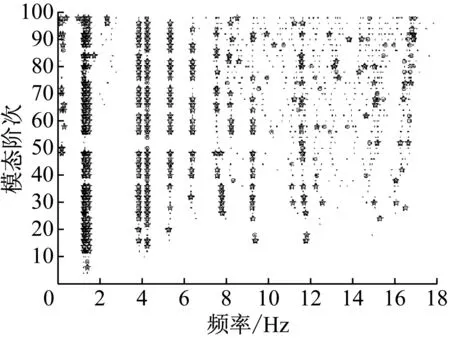
图4 SSI稳定图

图5 FCM聚类包含元素个数

将本文编写的基于SSI模糊聚类的自动识别方法和基于FDD与MAC阈值的自动识别方法，由表3结果可发现，该方法均能准确的识别出该结构的前6阶模态，也表明自动识别具有很强的鲁棒性可应用在未来的健康监测中。

5 结 论

针对目前自动识别方法的特点，虚假模态自动剔除要解决的关键问题是：① 在使用模糊聚类技术进行自动识别时如何确定聚类截断准则以及聚类中心数目;② 在使用指标自动剔除虚假模态时，如何选用合适的指标以及如何设定相应的阈值目前还缺乏比较与研究，尚未形成确定性的结论;③ 目前的自动识别方法大多针对某一种参数识别方法或者针对一类识别方法，还缺少一种能够囊括所有识别方法的一般性自动识别技术。

表3 不同识别方法的频率结果对比

由于自动识别技术在OMA识别技术中更有应用价值，在未来的自动识别方法研究中可充分结合OMA识别技术的特点，寻找一种更一般性的适用于与环境激励运营模态自动识别的方法，且能够对判断真假模态的指标及其阈值的选取做出分析与比较。

[1] SAS P. Modal analysis theory and testing[M]. Leuven: Katholieke Universteit Leuven, 2001.

[2] 高新波. 模糊聚类分析及其应用[M]. 西安：西安电子科技大学出版, 2004.

[3] MAGALHAES F, CUNHA A, CAETANO E. Online automatic identification of the modal parameters of a long span arch bridge[J]. Mechanical Systems and Signal Processing, 2009, 23(2): 316-329.

[4] 孙鑫晖, 张令弥. 宽频带模态识别算法中极点的自动选取[J]. 地震工程与工程振动学报, 2009, 29(1): 130-134.

SUN Xinhui, ZHANG Lingmi. Automatic pole selection for broad band modal identification[J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(1): 130-134.

[5] 孙国富. 基于模糊聚类的模态参数自动识别[J]. 振动与冲击, 2010, 29(9): 86-88.

SUN Guofu. Automatic modal parameters identification based on fuzzy clustering[J]. Journal of Vibration and Shock, 2010, 29(9): 86-88.

[7] BAKIR P G. Automation of the stabilization diagrams for subspace based system identification[J]. Expert Systems with Applications, 2011, 38(12): 14390-14397.

[8] PAPPA R S, ELLIOTT K B, SCHENK A. Consistent-mode indicator for the eigensystem realization algorithm[J]. Journal of Guidance Control and Dynamics, 1993, 16(5): 852-858.

[9] 汤宝平, 章国稳, 陈卓. 基于谱系聚类的随机子空间模态参数自动识别[J]. 振动与冲击, 2012, 31(10): 92-96.

TANG Baoping, ZHANG Guowen, CHEN Zhuo. Automatic stochastic subspace identification of modal parameters based on hierarchical clustering method[J]. Journal of Vibration and Shock, 2012, 31(10): 92-96.

[10] CABBOI A. Automatic operational modal analysis: challenges and application to historic structures and infrastructures[D]. Cagliari: University of Cagliari, 2013.

[11] REYNDERS E, HOUBRECHTS J, DE ROECK G. Fully automated (operational) modal analysis[J]. Mechanical Systems and Signal Processing, 2012, 29(5): 228-250.

[12] GOETHALS I, VANLUYTEN B, DE MOOR B. Reliable spurious mode rejection using self-learning algorithms[C]// Proceedings of the International Conference on Noise and Vibration Engineering. Leuven: ISMA, 2004: 991-1003.

[13] RAINIERI C, FABBROCINO G. Development and validation of an automated operational modal analysis algorithm for vibration-based monitoring and tensile load estimation[J]. Mechanical Systems & Signal Processing, 2015, 60/61:512-534.

[14] UBERTINI F, GENTILE C, MATERAZZI A L. On the automatic identification of modal parameters by subspace methods[C]// Proceedings of the EVACES 2011 Conference. Varenna: EVACES, 2011: 3-5.

[15] UBERTINI F, GENTILE C, MATERAZZI A L. Automated modal identification in operational conditions and its application to bridges[J]. Engineering Structures, 2013, 46(1): 264-278.

[16] HONG A L, UBERTINI F, BETTI R. Wind analysis of a suspension bridge: identification and finite-element model simulation[J]. Journal of Structural Engineering, 2010, 137(1): 133-142.

[17] 姜金辉, 陈国平, 张方,等. 模糊聚类法在试验模态参数识别分析中的应用[J]. 南京航空航天大学学报, 2009, 41(3): 344-347.

JIANG Jinhui, CHEN Guoping, ZHANG Fang, et al. Application of fuzzy clustering theory in experimental modal parameter identification analysis[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2009, 41(3): 344-347.

[18] VERBOVEN P, PARLOO E, GUILLAUME P, et al. Autonomous structural health monitoring—Part 1: modal parameter estimation and tracking[J]. Mechanical Systems & Signal Processing, 2002, 16(4):637-657.

[19] VERBOVEN P, PARLOO E, GUILLAUME P, et al. Autonomous modal parameter estimation based on a statistical frequency domain maximum likelihood approach[C]// Proceedings of International Modal Analysis Conference (IMAC). Kissimmee: Society for Experimental Mechanics,2001: 15111517.

[20] VANLANDUIT S, VERBOVEN P, GUILLAUME P, et al. An automatic frequency domain modal parameter estimation algorithm[J]. Journal of Sound & Vibration, 2003, 265(3):647-661.

[21] REYNDERS E, HOUBRECHTS J, DE ROECK G. Automated interpretation of stabilization diagrams[M].Modal Analysis Topics: Volume 3. New York: Springer, 2011: 189-201.

[22] SCIONTI M, LANSLOTS J P. Stabilisation diagrams: pole identification using fuzzy clustering techniques[J]. Advances in Engineering Software, 2005, 36(11): 768-779.

[23] LIU H, WU C, WAN H, et al. Parameter identification based on stabilization diagram with kernel fuzzy clustering method[C]//International Conference on Transportation, Mechanical, and Electrical Engineering (TMEE). Changchun: IEEE, 2011:1185-1188.

[24] AYVAZ M T, KARAHAN H, ARAL M M. Aquifer parameter and zone structure estimation using kernel-based fuzzy c-means clustering and genetic algorithm[J]. Journal of Hydrology, 2007, 343(3/4):240-253.

[25] MOORE B. Principal component analysis in linear systems: Controllability, observability, and model reduction[J]. Automatic Control IEEE Transactions on, 1981, 26(1):17-32.

[26] JUANG J N, PAPPA R S. An eigensystem realization algorithm for modal parameter identification and model reduction[J]. Journal of Guidance Control and Dynamics, 1985, 8(5): 620-627.

[27] GOETHALS I, DE MOOR B. Subspace identification combined with new mode selection techniques for modal analysis of an airplane[C]//13th IFAC Symposium on System Identification (SYSID 2003). Leuven：Katholieke Universteit Leuven，2003: 695-700.

[28] SCIONTI M, LANSLOTS J, GOETHALS I, et al. Tools to improve detection of structural changes from in-flight flutter data[J].Clinical & Experimental Immunology,2003,178(3)：470-482.

[29] DERAEMAEKER A, REYNDERS E, DE ROECK G, et al. Vibration-based structural health monitoring using output-only measurements under changing environment[J]. Mechanical Systems and Signal Processing, 2008, 22(1): 34-56.

[30] REYNDERS E, DE ROECK G. Reference-based combined deterministic-stochastic subspace identification for experimental and operational modal analysis[J]. Mechanical Systems and Signal Processing, 2008, 22(3): 617-637.

[31] LANSLOTS J, RODIERS B, PEETERS B. Automated pole selection: proof-of-concept & validation[C]//Proceedings of the ISMA International Conference on Noise and Vibration Engineering. Leuven: ISMA, 2004.

[32] VAN DER AUWERAER H, PEETERS B. Discriminating physical poles from mathematical poles in high order systems: use and automation of the stabilization diagram[C]//Instrumentation and Measurement Technology Conference. New York: IEEE, 2004: 2193-2198.

[33] LAU J, LANSLOTS J, PEETERS B, et al. Automatic modal analysis: reality or myth?[J]. Sound&Vibration, 2007, 1982: 17-21.

[34] VERBOVEN P, GUILLAUME P, CAUBERGHE B, et al. Stabilization charts and uncertainty bounds for frequency-domain linear least squares estimators[C]//Proceedings of the IMAC-XXI Conference and Exposition on Structural Dynamics. Kissimmee: Society for Experimental Mechanics,2003: 3-6.

[35] CHHIPWADIA K S, ZIMMERMAN D C, JAMES G H. Evolving autonomous modal parameter estimation[C]// Proceedings, International Modal Analysis Conference (IMAC). Kissimmee: Society of Photo-Optical Instrumentation Engineers, 1999: 819-825.

[36] GOETHALS I, DE MOOR B. Model reduction and energy analysis as a tool to detect spurious modes[C]//Proceedings of the International Conference on Noise and Vibration Engineering. Leuven: ISMA, 2002.

[37] ANDERSEN P, BRINCKER R, GOURSAT M, et al. Automated modal parameter estimation for operational modal analysis of large systems[C]// International Operational Modal Analysis Conference. Guimaraes: IOMAC, 2007: 299-308.

[38] BRINCKER R, ANDERSEN P, JACOBSEN N J. Automated frequency domain decomposition for operational modal analysis[C]// Proceedings of the 25th International Modal Analysis Conference (IMAC), Orlando: IMAC, 2007: 415.

[39] RAINIERI C, FABBROCINO G. Automated output-only dynamic identification of civil engineering structures[J]. Mechanical Systems and Signal Processing, 2010, 24(3): 678-695.

[40] 徐琪泽, 吴金志, 张毅刚. 基于振型相关性的结构模态参数频域自动识别[J]. 建筑结构, 2015(5):39-43.

XU Qize, WU Jinzhi, ZHANG Yigang. An automated frequency domain modal identification method based on modal assurance criterion[J]. Journal of Building Structures, 2015(5) :39-43.

[41] RAINIERI C, FABBROCINO G, COSENZA E. Automated operational modal analysis as structural health monitoring tool: theoretical and applicative aspects[J].Key Engineering Materials, 2007, 347: 479-484.

[42] RAINIERI C, FABBROCINO G, COSENZA E. Fully automated OMA: an opportunity for smart SHM systems[C]// Proceedings, International Modal Analysis Conference (IMAC). Orlando： Society for Experimental Mechanics,2009.

[43] RAINIERI C, FABBROCINO G, COSENZA E. An approach to automated modal parameter identification for structural health monitoring applications[C]// Proceedings of the Ninth International Conference on Computational Structures Technology. Stirlingshire： Civil-Comp Press,2008.

[44] RAINIERI C, FABBROCINO G, COSENZA E. An automated procedure for modal parameter identification of structures under operational conditions[C]// Materials Forum. Parkville:[s.n.], 2009: 33.

[45] LIU J M, YING H Q, SHEN S, et al. The function of modal important index in autonomous modal analysis[C]// Proceedings, International Modal Analysis Conference (IMAC). Orlando： Society for Experimental Mechanics,2007: 16.

[46] LIU J M, SHEN S, YING M, et al. The optimization and autonomous identification of modal parameters[M]. Modal Analysis Topics: Volume 3. New York: Springer, 2011: 203-214.

[47] 刘进明, 应怀樵, 章关永. OMA模态参数的优化及盲分析技术探讨[J]. 振动、测试与诊断, 2012, 32(6):1016-1020.

LIU Jinming, YING Huaiqiao, ZHANG Guanyong. Optimization of OMA modal parameter and technology study of blind analysis[J]. Journal of Vibration Measurement & Diagnosis, 2012, 32(6):1016-1020.

[48] PAPPA R S, WOODARD S E, JUANG J N. A benchmark problem for development of autonomous structural modal identification[C]// Proceedings of the 15th International Modal Analysis Conference. Orlando： Society for Experimental Mechanics,1997.

[50] JAMES G H, ZIMMERMAN D C, CHHIPWADIA K S. Application of autonomous modal identification to traditional and ambient data sets[C]// SPIE Proceedings Series. Kissimmee: Society of Photo-Optical Instrumentation Engineers, 1999: 840-845.

[50] PEETERS B, DE ROECK G. One year monitoring of the Z24-bridge: environmental influences versus damage events[C]//IMAC 18,the International Modal Analysis Conference. Leuven:Katholieke Universteit Leuven, 2000:1570-1576.

[51] BROWNJOHN J M W, CARDEN E P. Tracking the effects of changing environmental conditions on the modal parameters of Tamar Bridge[C]//3rd International Conference on Structural Health Monitoring and Intelligent Infrastructure. Vancouver: ISHMII, 2007.

[52] RAINIERI C, FABBROCINO G. Operational modal analysis of civil engineering structures[M]. New York: Springer, 2014.

[53] CHAUHAN S, TCHERNIAK D. Clustering approaches to automatic modal parameter estimation[C]//27th International Modal Analysis Conference. Orlando： Society for Experimental Mechanics,2009.

[54] MOHANTY P, REYNOLDS P, PAVIC A. Automated interpretation of stability plots for analysis of a non-stationary structure[C]//25th International Modal Analysis Conference (IMAC XXV). Orlando： Society for Experimental Mechanics, 2007.

[55] VERBOVEN P, CAUBERGHE B, PARLOO E, et al. User-assisting tools for a fast frequency-domain modal parameter estimation method[J]. Mechanical Systems and Signal Processing, 2004, 18(4): 759-780.

[56] PONCELET F, KERSCHEN G, GOLINVAL J C. Operational modal analysis using second-order blind identification[C]// 26th International Modal Analysis Conference. Orlando: IMAC, 2008.

[57] PHILLIPS A W, ALLEMANG R J. Additional mechanisms for providing clear stabilization (consistency) diagrams[C]//ISMA International Conference on Noise and Vibration Engineering. Leuven: Katholieke Universiteit Leuven, 2008.

[58] PHILLIPS A W, ALLEMANG R J, BROWN D L. Autonomous modal parameter estimation: methodology[M]//Modal Analysis Topics: Volume 3. New York: Springer, 2011: 363-384.

[59] BRINCKER R, VENTURA C. Introduction to operational modal analysis[M].[S.l.]:John Wiley & Sons, 2015.

[60] FELBER A J. Development of a hybrid evaluation system[D]. Vancouver: University of British Columbia, 1993.

Summary of methods eliminating spurious modes in automatic modal parametric identification

SONG Mingliang, SU Liang, DONG Shilin, LUO Yaozhi

(School of Architecture Engineering, Zhejiang University, Hangzhou 310058, China)

The key of automatic modal parametric identification is automatically eliminating spurious modes from identified modes. Here, methods eliminating spurious modes in automatic modal parametric identification were reviewed. Aiming at how to automatically eliminate spurious modes, the existing automatic modal parametric identification methods were divided into three categories including automatic analysis methods of stabilization diagrams based on intelligence algorithms, true and false modes automatic distinction methods based on index threshold values and automatic analysis techniques getting clearer stabilization diagrams based on improved identification algorithms. Detailed and comprehensive introductions to principles of the above three methods were presented. The characteristics, problems and future study directions of these methods were discussed. At last, combined with the measured acceleration data, representative automatic identification methods were used to automatically eliminate false modes of a reinforced concrete structure. The identified results using these methods were compared.

modal parameter; automatic identification; index threshold value; stabilization diagram; spurious mode; fuzzy clustering method

十二五国家科技支撑计划(2012BAJ07B03)

2016-04-12 修改稿收到日期：2016-05-09

宋明亮 男，博士生，1990年生

苏亮 男，博士，副教授，1975年生

TU311.3

A

10.13465/j.cnki.jvs.2017.13.001