空间机器人双目视觉测量系统精度分析

邸 男，田 睿

（中国科学院长春光学精密机械与物理研究所图像处理技术研究部，长春130033）

空间机器人双目视觉测量系统精度分析

邸 男，田 睿

（中国科学院长春光学精密机械与物理研究所图像处理技术研究部，长春130033）

鉴于现有的精度分析方法多为针对相机参数对精度影响的定性分析而缺少针对特定系统的量化分析模型，建立了双目测量系统数学模型，推导出相机参数、摆放角度、摆放基线、加工装调精度与系统精度之间的解析关系。利用该解析关系可以根据系统的精度要求，确定相机的参数、光学系统的安装精度、加工精度等参数，从而实现了可量化的系统设计，同时给出了完整的示例计算。

双目视觉测量；精度分析；误差分析；量化分析

1 引言

空间机器人的准确识别和定位需要航天员的控制，为使航天员对外界环境具有身临其境的感觉，目前多采用双目视觉测量系统，将机器人所观察到的场景真实地反映到航天员的视野中［1］。因此，双目视觉测量系统的精度直接关系空间机器人的工作成效［2⁃3］。

目前，许多学者对双目立体视觉系统精度进行了深入的研究，但大部分研究都是从理论方面讨论几何参数对已建立的双目立体视觉系统测量精度的影响，如文献［4］分析了数字量化效应对精度的影响；文献［5⁃7］讨论了光轴与基线的夹角、基线长度、焦距等对系统测量精度的影响，但是没有联系实际论述物距对系统精度的影响；文献［8］分析了摄像机标定精度、镜头参数及系统结构参数对系统测量精度的影响。

目前已知双目立体视觉系统精度与空间点在图像平面的成像误差密切相关，该误差由相机的内部结构误差产生，但目前大部分研究对相机内部误差讨论较少，因此常将空间点成像误差近似取1像元或0.5像元。本文试图建立相机内部误差与空间点成像误差间的解析关系，确定成像误差。将该误差带入到精度计算模型中，从而得到相机内部误差与系统精度之间的解析关系，即建立了系统设计与精度之间的联系，保证系统满足精度要求。

工程系统设计过程中，焦距、基线、工作范围、加工误差等参数都有约束，这些约束决定了系统设计需要确定一个比较合理的参数集。本文试图建立精度和影响精度的参数之间的关系，从而能根据精度需求确定出相机的焦距、基线、摆放角度、加工允许误差等参数，作为项目设计的依据。

2 双目立体视觉系统的误差分解

从相机成像模型［2］可以看出，空间任一点P的位置误差主要受两方面因素影响：

1）相机内部误差

（1）相机的内部结构误差：包括相机的成像平面与光学系统光轴间的旋转误差以及实际成像平面与理想平面的偏移误差。

（2）相机标定设备的误差：相机成像平面与光学系统组合装调时使用的标定设备，二维转台测角与调平误差，平行光管调平与自准直误差，经纬仪调平与自准直误差和相机安装误差。

（3）图像中点的提取精度：空间任意点在左右相机中成像位置提取的误差。

2）相机外部误差

两相机间的外部参数（两个相机间的位姿矩阵）的误差，包括摆放角度和基线误差。

2.1 相机内部误差

2.1.1 相机内部结构误差

通过相机内部机械结构可知，影响成像点坐标的因素包括：

1）光学系统光轴与成像系统的成像面不垂直，即成像面倾斜，倾斜角度为θ，相机视场角的一半为α，如图1所示。根据正弦定理得式（1）～（2）：

2）实际成像面虽与理想成像面平行，但是偏离了理想成像面，如图2所示。根据图2，得到式（3）：

其中Δf最大值为f tanαtanθ，则有式（4）成立：

3）成像面绕光轴旋转ϕ，如图3所示。

视场边缘入射光线与光轴夹角为α，则有式（5）成立：

2.1.2 相机标定设备误差

在相机内参数标定过程中，标定设备误差主要包括：二维转台测角与调平误差，平行光管调平与自准直误差，经纬仪调平与自准直误差和相机安装误差。二维转台测角与调平误差均为10″，服从正态分布；平行光管调平与自准直误差均为10″，服从正态分布；经纬仪调平与自准直误差均为10″，服从正态分布；相机安装误差为10″，服从正态分布；根据误差合成，δ＝26.46″。则标定设备产生的像元偏差如式（6）所示：

2.1.3 算法精度

由于噪声、光照变化及透视畸变等因素影响，空间任意点在两相机像面上投影的对应点的特性可能不同，为提高匹配精度，需利用另外的信息或约束条件作为辅助判据，以提高匹配精度。一般采用边缘点检测方法获得图像中的边缘点，采用经典的基于灰度相关的区域匹配方法建立特征点间初始候选匹配关系，经过对称性测试，建立特征点间的对应关系，然后对候选匹配点采用基于视差梯度约束消除部分虚假匹配，再对剩下的点进行鲁棒性估计算法求解基本矩阵，再次消除部分虚假匹配，建立高精度立体匹配对应点，根据建立的准确匹配关系，计算高精度基本矩阵。在此基础上，进行更多对应特征点的匹配。如此计算的匹配精度可保证Δ5不超过0.5个像元。

2.2 外部标定误差

由于加工及装调等因素，相机坐标系与基准棱镜坐标系不能完全重合，需利用平行光管、经纬仪及高精度二维转台来测量基准棱镜坐标系与相机坐标系间的角度误差，进而确定旋转矩阵误差，将平行光管水平放置，二维转台水平轴水平并与平行光管光轴垂直放置，竖直轴垂直，二维转台与平行光管构成的坐标系与相机坐标系保持一致。

以左相机为例，先用经纬仪自准直左基准棱镜yj轴，测得yj轴在左相机坐标系内x1o1y1面投影与y1轴的夹角β1；对二维转台进行上下转动，使平行光管与左基准棱镜zj轴高低方向进行自准，测得zj轴在x1o1y1面投影与z1轴的夹角γ1；对二维转台进行方位旋转，使平行光管与左基准棱镜xj轴方位自准，测得xj轴在y1o1z1面投影与x1轴的夹角为α1。

测量中的误差包括：二维转台调平及测角误差δ1＝δ2＝10″、经纬仪调平及自准直误差δ3＝δ4＝10″、光管调平及自准直误差为δ5＝δ6＝10″、相机安装误差为δ7＝10″、棱镜加工误差δ8＝10″，且均服从正态分布。

测量角α1所涉及到的误差源包括：二维转台调平及测角误差、平行光管调平及自准直误差、相机安装误差及棱镜加工误差，则测量角α1的误差如式（7）所示：

测量角β所涉及到的误差源包括：二维转台调平及测角误差、平行光管调平及自准直误差、相机安装误差及棱镜加工误差，则测量角β的误差如式（8）所示：

测量角γ所涉及到的误差源包括：二维转台调平误差、经纬仪自准直及调平误差、相机安装误差及棱镜加工误差，则测量角γ的误差如式（9）所示：

标定右相机坐标系旋转到左相机坐标系的转换矩阵过程中存在的误差因素包括：经纬仪自准直及调平误差均为10″、二维转台调平误差10″、相机坐标系的标定误差38″，则右相机坐标系旋转到左相机坐标系的角度误差如式（10）：

2.3 示例计算

示例：双目视觉测量系统相机焦距f为12 mm，像元尺寸为4.8μm，相机装调最大偏角，相机视场角一半α＝21°，则根据2.1节的误差计算公式（4）、（6）～（8）可得式（11）：

即该双目测量系统的内部误差导致的空间点在图像中的偏移最大为0.7515像元。

3 双目像机摆放和工作范围分析

3.1 建立解析关系

建立图4所示相机的工作范围d1～d2与相机的摆放角度α和基线B之间的解析关系，从而确定双目相机的摆放。

根据图5，有式（12）～（14）成立：

其中ω为相机的视场角，m为相机视场水平覆盖范围。

3.2 示例计算

示例：基线为200 mm，测量距离为350～800 mm。分析像机光轴与水平夹角与水平覆盖视场范围的关系。图5显示不同水平夹角时，水平方向视场的覆盖范围。当相机光轴与水平夹角为79°时，距离350 mm时水平方向视场覆盖范围为237.4 mm，距离800 mm时水平方向视场覆盖范围为482.1 mm，如图5所示。

4 双目像机的测量精度分析

4.1 测量位置精度分析

分析双目立体视觉配置以及参数对精度的影响，为了分析影响因素以及影响程度，建立如图6的精度分析模型。

方便起见，把视觉测量系统的坐标原点建立在其中一台相机的投影中心。设两个相机的有效焦距分别为f1、f2，两个相机的投影中心分别为O1、O2。

投影中心之间的距离即为基线距B。基线距B与相机两个光轴的夹角分别是α1、α2。空间一点P（x，y，z）在xz平面的投影点为P′，O1P、O2P与O1、O2的夹角分别记为ϕ1、ϕ2，O1P′、O2P′与两个相机光轴的夹角分别ω1、ω2，P点在左、右相机成像平面坐标点分别为（X1，Y1），（X2，Y2）。

根据图7中的几何关系，可以得到式（15）：

z即为目标点P到测量系统的距离，由上图的几何关系还可以得到表达式（16）：

由（15）、（16）两式，任意空间一点P的三维坐标可以表示为式（17）：

进一步由图6的几何关系，在X1O1Y1、X2O2Y2坐标系中，可得到表达式如式（18）：

根据针孔成像原理，可知有式（19）、（20）成立：

求偏导数计算系统精度如式（21）～（24）：

为简化分析，令f1＝f2＝f，α1＝α2＝α，这里给出在相机基线的垂直平分线上点的测量精度，因此ω1＝ω2＝ω，距离测量精度如式（25）～（27）：

其中Δ为第3节计算得到的综合成像偏差。

4.2 绕x轴旋转精度分析

空间点P绕x轴旋转α度时，P′的成像示意图如图7所示。

对式（18）求偏导得式（28）～（30）：

综合考虑2.2节相机外部参数误差影响，绕x轴旋转精度如式（31）：

4.3 绕y轴旋转精度分析

空间点P绕y轴旋转β度时，P′的成像示意图如图8所示。

对式（20）求偏导得式（32）～（34）：

综合考虑2.2节相机外部参数误差影响，绕y轴旋转精度为式（35）：

4.4 绕z轴旋转精度分析

空间点P绕z轴旋转γ度时，P′的成像如图9所示。

由于γ很小，此时y方向的变化量会远大于x方向变化量，因此仅考虑x方向变化，其中a／2为视场覆盖范围的一半，则有式（36）、（37）：

综合考虑2.2节外部参数误差影响，绕z轴旋转精度为式（38）：

4.5 示例计算

根据公式（25）～（27）计算不同距离下的x、y、z轴距离精度如表1所示。

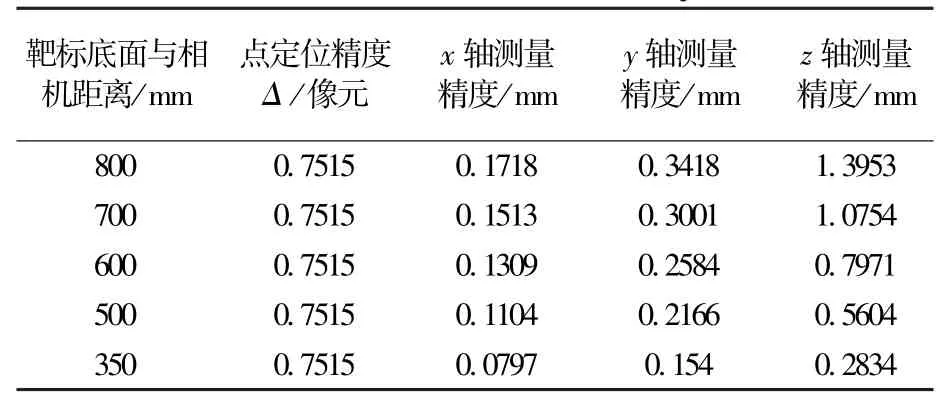
表1 距离测量精度Table 1 Distance accuracy

根据公式（31）、（35）、（38）计算不同距离下的绕x轴、y轴、z轴旋转精度如表2所示。

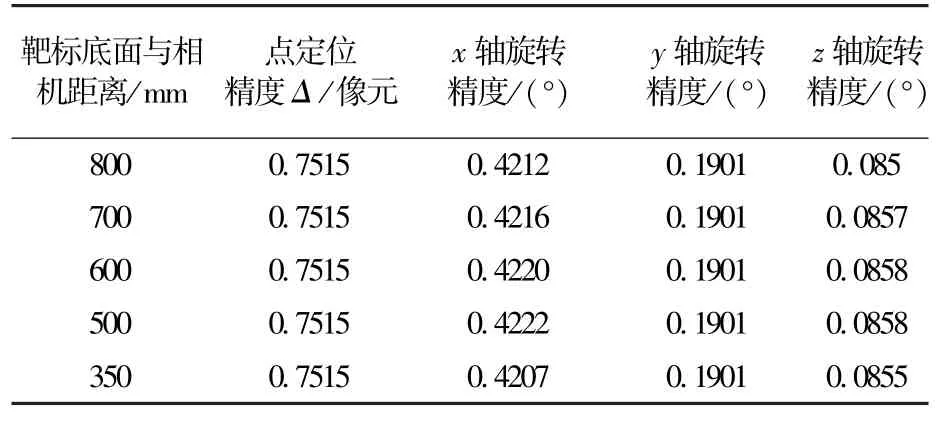
表2 旋转精度Table 2 Rotating accuracy

5 结论

本文通过分析双目视觉测量系统中对精度产生影响的误差因素和对相机内部误差和外部误差进行建模，给出的系统精度计算方法，能够得出不同物距下的系统精度理论值作为系统设计前的指导参考值，能够在精度值无法满足系统指标要求时通过调整输入参数、控制装调误差等方式，使精度达到理论设计需求。

（References）

［1］ 张广军.机器视觉［M］.北京：科学出版社，2005：134⁃201. Zhang Guangjun.Machine Vision［M］.Beijing：Publishing Company of Science，2005：134⁃201.（in Chinese）

［2］ 董圣男.基于双目立体视觉的空间非合作目标的位姿测量［D］.南京：南京航空航天大学，2010. Dong Shengnan，The Pose Measurement for Space Non⁃Coop⁃erative Target Based on Stereo Vision［D］.Nanjing：Nanjing University of Aeronautics and Astronautics，2010.（in Chi⁃nese）

［3］ 支帅.非合作目标双目视觉测量系统误差理论研究［D］.长春：中国科学院长春光学精密机械与物理研究所，2014. Zhi Shuai.Research on the Error Theory of Binocular Vision Measurementsystem on Non⁃cooperative Target［D］.Chang⁃chun：Changchun Institute of Optics，fine Mechanics and Physics，ChineseAcademy of Sciences，2014.（in Chinese）

［4］ Bradley D，Heidrich W.Binocular camera calibration using rectification error［C］／／Computer and Robot Vision（CRV），2010 Canadian Conference on.IEEE，2010：183⁃190.

［5］ Klaus A，Sormann M，Karner K.Segment⁃based stereomatc⁃hing using belief propagation and a self⁃adapting dissimilarity measure［C］／／18th International Conference on Pattern Rec⁃ognition（ICPR′06）.IEEE，2006，3：15⁃18.

［6］ 刘亚菲，郭慧，聂冬金，等.双目立体视觉系统测量精度的分析［J］.东华大学学报（自然科学版），2012，38（5）：572⁃576. Liu Yafei，Guo Hui，Nie Jindong，et al.Analysis on meas⁃urement accuracy of binocular stereo vision system［J］.Jour⁃nal of Donghua University（Natural Science），2012，38（5）：572⁃576.（in Chinese）

［7］ 孟环标.双目视觉测量系统误差分析与控制［D］.济南；山东大学，2012. Meng Huanbiao.Error Analysis and Control of Measurement System Based on Binocular Vision［D］.Jinan：Shandong Uni⁃versity，2012.（in Chinese）

［8］ 肖志涛，张文寅，耿磊，等.双目视觉系统测量精度分析［J］.光电工程，2014，41（2）：6⁃12. Xiao Zhitao，ZhangWenyin，Geng Lei，etal.Accuracy anal⁃ysis of binocular vision system［J］.Opto⁃Electronic Engineer⁃ing，2014，41（2）：6⁃12.（in Chinese）

Precision Analysis of Binocular Vision M easurement System in Space Robots

DINan，TIAN Rui
（Department of Image Processing，Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China）

The current precision analysismethods aremainly focusing on the qualitative analysis of the effects of the camera parameters on the precision instead of the quantitative analysis of the specif⁃ic system.In this paper，amodel for the binocular vision measurement system was established and analytical relationship among the camera parameters，the fix angle，the base line，the machining precision and the system precision was derived.On this basis，the camera parameters，the installa⁃tion precision and themachining precision of the optical system could be determined according to the precision requirements of the system.Thus the quantifiable system design could be realized and a complete calculation example was given.

binocularvision measurement system；precisionanalysis；error analysis；quantitative analysis

TP391.41

A

1674⁃5825（2017）01⁃0076⁃06

2015⁃08⁃10；

2016⁃08⁃16

邸男，女，博士，副研究员，研究方向为视觉测量。E⁃mail：din＠ciomp.ac.cn