培养高中生数学发散性思维的四种策略

陈家祥

【摘 要】本文论述通过一题多解、多元变换、数形结合、链接生活等方法，探讨如何培养高中生数学发散性思维。

【关键词】高中数学 发散性思维 数形结合

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2017）05B-0130-02

美国心理学家吉尔福特曾经说过：人的创造力，主要依靠发散性思维，它是创造性思维的主要成分。由此可见，培养学生的发散性思维，有利于促进学生创造性思维的形成。在高中数学教学的过程中，教师必须重视学生思维方式的培养和锻炼，特别是发散性思维。发散性思维相似于求异思维却又区别于传统思维，在解决数学问题时，学生大多习惯于用传统的思维模式去分析问题，然而这种思路在解决很多数学问题时，常常会受阻。因此，教师在教学过程中就要注意培养学生的发散性思维，不要拘泥于单一的传统固定思维模式。下面，笔者将结合自身的经验，谈一些在教学中如何培养学生发散思维的做法。

一、一题多解，触及本质

对于同一道题，从不同的角度去分析研究，可能会得到不同的思路与启示，从而找到不同的解法。同时，教师也应注意，过多的、盲目的做题会抑制学生思维的发展，容易使其感到疲劳，丧失对数学的兴趣。因此，教师在教学过程中，应该注意精选题目，引导学生进行一题多解，不仅有助于拓展和解放学生的思维，也更容易触及问题的本质，从而巩固学生的知识，调动思维的积极性，有效培养学生的发散性思维。

比如笔者在对“等差数列的前 n 项和”这部分内容进行教学时，对下面道例题采取了一题多解的策略进行教学。

已知 {an} 为等差数列，其前 10 项的和 S10=100，前 100 项的和 S100=10，求前 110 项的和 S110。

笔者向学生提问：“这道题同学们能探索出几种解法呢？”然后留给学生充分的时间去思考和探究。学生最快想到的解题方法是通过利用等差数列的表达式列方程求出首项和公差，进而利用求和公式求解，即利用方程思想求解。

设该数列首项为 a1，公差为 d，，解得 a1=10.99，d=-0.22。进而求出 ，由此得到正确答案。但是仅仅用这一种方法解题并不够，接下来，笔者再给学生一个提示：利用函数思想或者利用等差数列的性质还可以有不同的解答方法。函数思想即为待定系数法，设数列的前 n 项和为 Sn=An2+Bn，则 100A+10B=100，10000A+100B=10，解得 A=-0.11，B=11.1，进而求出 S110=A×1102+B110=-110。第三种解题方法是利用等差数列的性质：S100-S10=-90=，而 a11+a100= a1+a110=-2，所以 S110==-110。

在上述教学活动中，笔者注意引导学生从不同角度、不同思路解决同一道问题，通过这种一题多解的训练，不但巩固了学生对于这部分的知识，还能复习其他内容的知识，学生的发散性思维就能够在这种一题多解的练习中逐渐培养起来。

二、多元變换，建构体系

一题多解是培养学生发散性思维的好方法，同时，一题多变也有利于训练学生的发散性思维，因为这种训练能够帮助学生熟练运用所学知识，建构和完善知识体系，学生的解题灵活性也能得到提高。采用这种方法时，教师可以对问题进行多元变换，也可以改变条件、改变图形、改变问题等等，可以是由浅入深的变化，让学生理解的层次不断加深。

比如笔者对“三角函数”这部分知识进行教学时，为了培养学生学会灵活转化三角函数和熟练利用三角函数公式，采取了一题多变的教学策略。以下面这道例题为例：已知 ，且 a 是第二象限角，求 tana。看到这道题，学生首先利用所学的知识解答：因为 a 为第二象限角，因此由已知条件得，。接下来笔者对这一例题进行了变换。变式一：若已知求 tana。变式二：已知 sina=m（m>0），求tana。变式三： 求 tana。这三个变式的难度由浅入深，学生通过对这三个变式的练习，就能逐渐掌握正弦值在不同情况下转化为正切值的方法：当 a 的正弦值 m 为 1 或 -1 时，正切值不存在；当 m=0 时，正切值也为 0；当 a 为一、四象限角时，；当 a 为二、三象限角时，。

在上述教学活动中，笔者正是通过对一道题进行多元变换，使学生建构了关于“转化三角函数和熟练利用三角函数公式”这部分内容的知识体系。学生的发散性思维在这样的练习中得到不断的提升。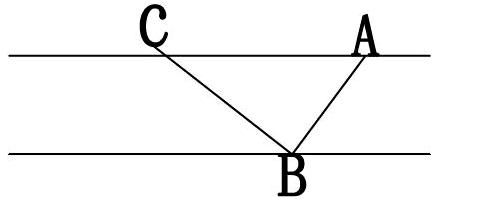

三、数形结合，学会联想

数形结合思想是数学四大思想之一，它兼具了数的严谨与形的直观之长，通过数与形之间的对应和转化来解决数学问题，能够使复杂的问题简单化、抽象问题具体化。由此可见，数形结合思想对于学习数学来说是一种非常重要且实用的思想方法。因此教师在教学过程中应当不断渗透数形结合思想，引导学生学会联想，通过数形结合快速准确地求解问题，从而发展学生的发散性思维。

比如笔者在对“不等式”这一章节的内容进行教学时，对于下面这道例题就采用了数形结合的思想来解：已知的解集为，求实数 a 的值。

首先，笔者先引导学生运用解方程的思想解决这道题：从已知条件可知 x=-4 与 x=-2 是方程的两个根，将其代入方程中可得到或，进行检验后，满足已知条件，所以是这道题的正确答案。

用这种方法求解该问题需要进行大量的计算，耗时较长。接下来笔者引导学生利用数形结合的思想求解，体会这种方法的优点。

设，设，在同一直角坐标系中分别画出这两个函数的图象。则的图象意义为函数 y1 的图象在函数 y2 图象上方时 x 的取值范围。观察图象可发现，当直线通过（-2，2）这一坐标时，满足 y1≥y2 的 x 取值范围为[-4，-2]，将点（-2，2）代入 中，就能得出 。

在上述教学，笔者通过将数形结合求解问题的方法与常规方法进行对比，使学生更为直观地感受到数形结合思想在解答数学题时的快速与便捷，促进学生在解题时更多地使用数形结合思想去分析问题，从而打开解题思路。学生的发散性思维通过数形结合的训练得到了发展。

四、链接生活，引导应用

新课标强调，教学要生活化，必须将课本知识与实际生活紧密结合。因此教师在教学过程中应当努力使数学教学更为生活化，通过将课本上的知识链接到生活中来，引导学生运用数学知识解决生活中的数学问题，这样不但有利于提高学生的创新能力，发展创造性思维，也有利于培养学生的发散性思维。

比如笔者在对“正弦定理和余弦定理”这一节的课本内容教学完后，为了强化学生对该知识的应用，笔者联系生活设计了一道探究题：如图所示，在一条江的两岸有 A、B 两点，试设计出一种测量方法测出 A、B 两点之间的距离。学生通过思考、分析与讨论，最后设计出一种应用正弦定理求出距离的方法：在测量者同侧另选一点 C，然后分别测出 AC 的距离和∠BAC和∠ACB 的大小。进而由正弦定理可得，，代入测量数据即可求出 A、B 两点之间的距离。紧接着筆者又提问道：“为什么选择利用正弦定理而不是余弦定理呢？”学生立即回答：“因为 BC 的距离不能直接测量，所以余弦定理无法应用。”由此可见，学生对正弦定理和余弦定理已经有了深刻的认知，并且能够在生活中灵活应用正余弦定理的公式。

在上述教学活动中，笔者通过将知识链接到生活，引导学生自主利用所学知识探究出问题的答案，不但活跃了学生的思维，还有助于加强学生的发散性思维，而教师的教学目标也能高效完成。

通过上述的实践探究，笔者发现，只要教师在教学中通过采取一题多解、多元变换、数形结合、链接生活等策略，就能够有效地培养学生的发散性思维，打开学生的解题思路，使其体会到思考的乐趣、数学的乐趣。

【参考文献】

[1]张 蕾.高中数学教学中学生发散性思维的培养[J].现代教育科学，2014（6）

[2]水莉莉，周 霞.高中生数学发散思维培养过程中存在的问题及解决办法[J].科教导刊，2015（5）

[3]王海龙.高中学生数学发散性思维的培养策略[J].科技视界，2013（29）

（责编 韦 力）