Chebfun系统下对《数值分析》课程教学的新认识
2017-07-12马俊杰刘惠篮何清龙
马俊杰+刘惠篮+何清龙
摘 要:《数值分析》是介绍科学计算方法的基础性课程,对培养学生的科学计算素质起关键性作用。针对《数值分析》课程教学的几个问题,本文在新古典主义数值分析角度下探讨了本课程的改革措施。
关键词:数值分析 教学改革 教学内容 教学方法
中图分类号:G642 文献标识码:A 文章编号:1672-1578(2017)06-0023-02
1 引言
《数值分析》是计算数学方向的基础课程,是教授针对实际问题设计数值算法的一门课程。这门课程主要研究数值逼近问题、数值积分问题、微分方程数值解问题以及线性方程组数值解问题等,是数学与应用数学专业、信息与计算科学专业的专业基础课,也是统计学专业必修的专业课之一。《数值分析》课程具有集数学理论与程序设计于一身的特点。在实际教学中,教师既需要以严谨的科学性传递给学生基本数学知识,又要教授学生在计算机上实现算法的能力。
2 课程发展现状
我国电子计算机的应用始于上世纪50年代,为了满足其对高素质科学计算人才的需求,国内大学相继开设了数值计算方法、程序设计等课程。1977年10月的教材会议上,计算数学的专业基础课被划分为三个方向,即数值逼近、数值代数以及微分方程数值解。分别采用李岳生和黄友谦编写的《数值逼
近》[1],黄志浩、张玉德和李瑞遐编写的《矩阵计算与方程求根》[2]以及李荣华和冯果忱编写的《微分方程数值解法》[3]作为教材。之后,计算数学专业经历了两次改名,分别是1987年更名为计算数学及其应用软件专业,1998年更名为目前的信息与计算科学专业。从这两次的更名可以看出计算数学的专家学者已经深刻意识到,计算数学既是一门数学科学又是一门语言科学。在更名为信息与计算数学专业后,计算方法课程在原先三门课的基础上更名为《数值分析》。其内容包括之前的数值逼近、数值代数以及微分方程数值解三个部分。
当代学者一般认为,《数值分析》课程存在课程教学内容多、教学学时少,教学过程中重视理论、忽视应用,教学过程中缺少“可视化”过程,课程考核方式不合理等问题[4]。针对这些问题,现有文献给出了许多改革建议。例如,李小林认为本课程的实践教学环节可分为两方面的内容[5]。一方面让学生对典型的算法进行学习,另一方面在课程结束后,让学生分组完成一些综合性课题。针对地质工程数值法的教学问题,黄雨和刘铖玮提出目前教材的教学内容更新慢,且过于繁琐。在实际教学中,应该注重因材施教,灵活调整教学重点[6]。刘秀娟,李久会和徐美进指出本课程的考核方式应趋于科学化、合理化。总评成绩应包含平时成绩、上机成绩和期末成绩。其中平时成绩主要考核学生的学习态度,上机成绩主要考察学生上机解决问题的能力,而期末成绩主要考查学生对基础知识的理解[7]。下面,我们将以Chebfun系统为基础,探讨《数值分析》课程改革的新方向。
3 教学改革建议
Chebfun系统是牛津大学的Nick Trefethen教授在Matlab环境下开发出的可供计算数学科研人员与教学人员使用的工具箱。
3.1 课程内容多,教学课时少
由于本课程涵盖的内容广泛,包括微积分、线性代数、常微分方程、泛函分析等,学生必须在具有牢固的基礎上才能学好本课程。为了解决这一问题,授课教师可以根据学生的实际情况选择合适的教材,或者自行编写适合本学校的教材。这不仅可以提高教学效率,而且可以提高学生对本课程的兴趣。Nick Trefethen教授在开发Chebfun系统的同时编著了相关指导书《Approximation Theory and Approximation Practice》[8]。全书并无一处复杂的数学推导,却将计算数学中的基础知识点讲的清清楚楚,是这种教学方式的成功典范。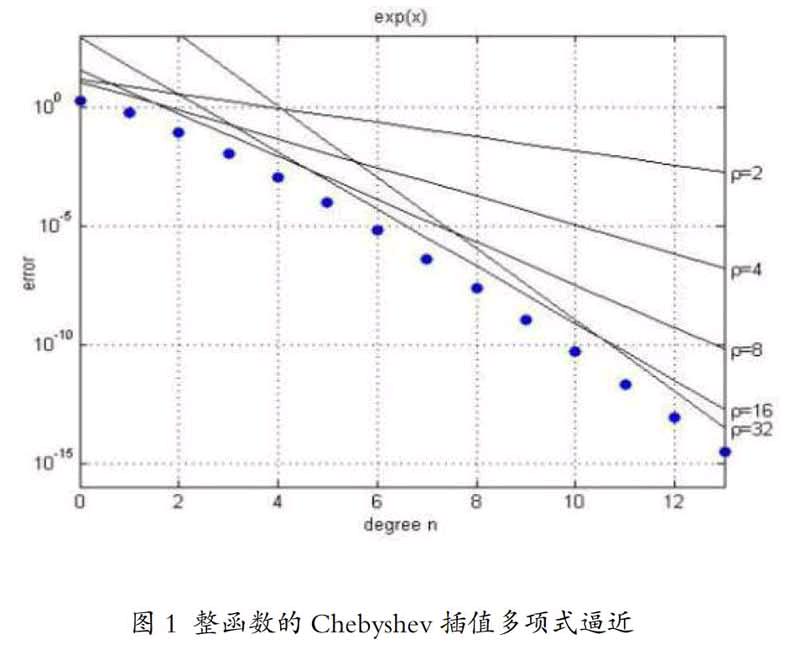
3.2 教学过程重视理论、忽视应用
计算数学是一门来源于现实问题的学问,在其教学过程忽视学生实际动手能力的培养无疑是一种舍本逐末的教学方式。但是,由于实际问题的复杂性,高校教师很难将这些问题改造为可供本科生操作的问题。这一矛盾可以借助Chebfun系统提供的简洁算例得到解决。下面的代码给出了Bernstein多项式的构造方法:
function BernsteinPolys()
LW = 'linewidth'; lw = 1.6;
s = chebfun('s',[0 1]);
f = min(abs(s-.3),2*abs(s-.7));
f = s + max(0,1-5*f);
hold off, plot(f,LW,lw)
function Bn = Bn(f,n)
warning off
x = chebpts(n+1,[0 1]);
Bndata = zeros(size(x));
for k = 0:n
Bndata=Bndata+f(k/n)*nchoosek(n,k).*x.^k.*(1-x).^(n-k);
end
Bn = chebfun(Bndata,[0 1]);
warning on
end
end
通过讲解这段代码,可以在将最佳一致逼近问题教授给学生的同时,也可以使学生熟悉Matlab语言,进一步加强实际动手能力。在实际教学过程中,我们发现这种教学方式提高了学生的主观能动性,激发了学生的学习兴趣,对教学效果的提升有很大帮助。
3.3 教学过程中缺少“可视化”过程
使用计算机解决实际问题的一般过程包括:实际问题、数学建模、算法设计、算法实现、数值结果。如果只让学生被动的记忆这个过程,无疑会对教学效果产生负面效果。因此,在整个过程中,通过引入图像的方式加强学生对数值分析基本定理的理解是十分重要的教學手段。在Chebfun系统中,开发者基于新古典主义数值逼近的新进展设计了许多此类算例。考虑整函数的Chebyshev插值问题。对于[-1,1]上的函数f,其n次插值多项式pn的逼近精度以O(ρ-n)的速度收敛,这里的ρ函数f的解析半径。以指数函数f(x)=ex为例, 在Matlab环境下可以计算其解析半径如下图:
通过数值结果,学生可以很明确的看到Chebyshev插值多项式的指数收敛性质。
4 结语
《数值分析》是高等学校信息与计算科学专业的基础课程。本文以新古典主义数值分析的角度,通过分析本课程面临的一些问题,提出了《数值分析》课程教学的新方式。但是,值得注意的是教学改革是一项长期任务。在以后的教学过程中,我们仍需要在新视角下选择合适的教学内容,创新教学手段,总结教学经验,不断提高教学水平。
参考文献:
[1] 李岳生,黄友谦.数值逼近[M].北京:人民教育出版社,1978.
[2] 黄志浩,张玉德,李瑞遐.矩阵计算与方程求根[M].北京: 人民教育出版社, 1979.
[3] 李荣华,冯果忱. 微分方程数值解法[M].北京: 高等教育出版社,1980.
[4] 杜廷松.关于《数值分析》课程教学改革研究的综述和思考[J]. 大学数学,2007; 23(2):8-15.
[5] 李小林.关于数值计算方法课程教学改革的探讨[J].重庆文理学院学报(自然科学版),2010; 29(2):85-87.
[6] 黄雨,刘铖玮.工程数值法教学改革研究—以“地质工程数值法”为例[J].高等建筑教育,2013; 22(4):81-84.
[7] 刘秀娟,李久会,徐美进.信息与计算科学专业数值分析课程实践教学改革[J].辽宁工业大学学报(社会科学版),2014,16(4):83-86.
[8] N.Trefethen. Approximation Theory and Approximation Practice [M]. Philadelphia: SIAM, 2013.
作者简介:马俊杰(1986-),贵州贵阳人,男,博士,贵州大学数学与统计学院讲师,研究方向:计算数学。
刘惠篮(1988-),贵州贵阳人,女,博士,贵州大学数学与统计学院讲师,研究方向:统计建模。
何清龙(1987-),贵州贵阳人,男,博士,贵州大学数学与统计学院讲师,研究方向:计算数学。
