涉及极点重级与分担值的亚纯函数正规定则
2017-07-12林琼叶亚盛俞伟鹏
林琼,叶亚盛,俞伟鹏
(上海理工大学理学院,上海 200093)
涉及极点重级与分担值的亚纯函数正规定则
林琼,叶亚盛,俞伟鹏
(上海理工大学理学院,上海 200093)
运用分担值的思想证明了涉及极点重数的亚纯函数族的正规定则,所得结论推广了相关文献的主要结果.
极点重数;分担值;正规族
1 引言
文献[1]证明了如下著名的定理.
定理 A设 f是复平面C上的亚纯函数,n(≥5)是正整数,a(≠0),b是两个有穷复数.如果 f′+afn≠b,则 f 恒为常数.
文献[2]提出了相应的正规定则,被许多学者相继研究,得到如下结论,见文献[3-8].
定理 B设F是区域D内的一族亚纯(全纯)函数,n,k是正整数,a(≠0),b是两个有穷复数,如果 n≥k+3(n≥2),并且 ∀f∈F,有 f(k)+afn≠b,则 F 在 D 内正规.
文献[9]利用分担值的思想证明了如果函数族中的任意一个函数和它的一阶导数分担三个有穷复数,则该函数族在区域D内是正规的.文献[10]在定理B的基础上考虑极点重数,证明了如下结论.
定理 C设k是正整数,a(≠0),b是两个有穷复数,F是区域D内的一族亚纯函数,族中每个函数的极点重数至少为k+2.如果∀f∈F,有f(k)+af3≠b,则F 在 D 内正规.
2012年文献[11]用分担值的思想推广了定理B.
定理 D设n,k(n≥k+3)是两个正整数,a(≠0),b是两个有穷复数,F是区域D 内的一族亚纯函数,族中每个函数的零点重数至少为 k.如果∀f,g∈F,有
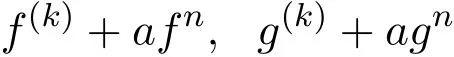
在 D 内分担 b,则F在D内正规.
本文将定理C与定理D推广到了更一般的情形
定理 1.1设 n(≥ 3),k是正整数,a(≠0),b是有穷复数,F 是区域 D 内的一族亚纯函数,族中每个函数的零点重数至少为 k,极点重数至少为 k+1.如果 ∀f,h∈F,有L(f)+afn与L(h)+ahn在D内分担b,其中

则F在区域D内正规.
例 1.1设是k≥2正整数,

则对于F中任意两个函数f,h,f(k)+afn与h(k)+ahn在D内分担0,但是F在D内不正规.
这说明定理1.1中的条件”族中每个函数的零点重数至少为k”是必要的.
例1.2设
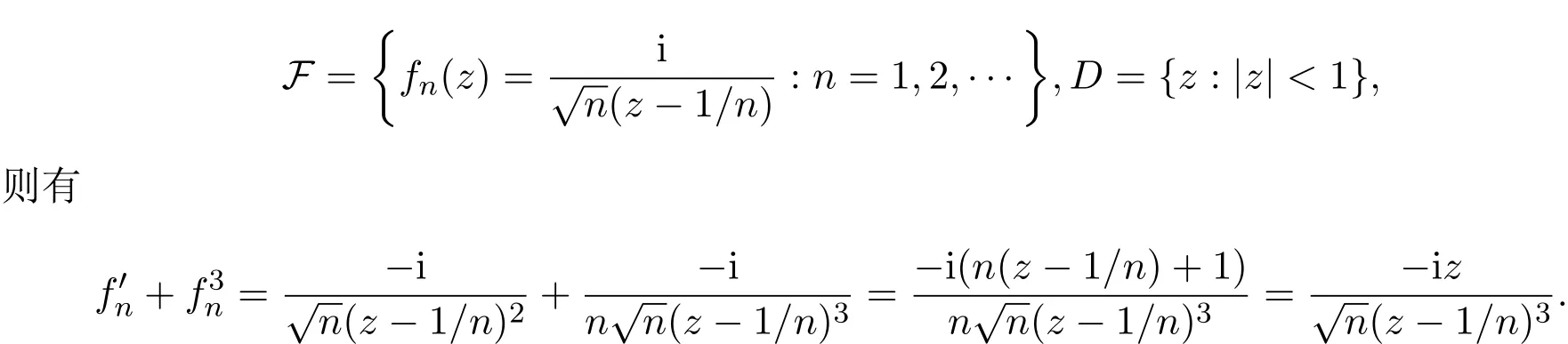
即 f′+af3与 h′+ah3在D 内分担0,但是F 在D 内不正规.
这说明定理1中的条件”族中每个函数的极点重数至少为k+1”是必要的.
2 主要引理
为了完成定理1.1的证明,需要以下引理
引理 2.1[12-13]设F是单位圆盘△上的一族亚纯函数,且族中任意函数的所有零点重级均至少为p,所有极点重级均至少为q.设α是一个满足−p<α (a)点列zn∈△,zn→z0; (b)函数列fn∈F; (c)数列 ρn→0+, 引理 2.2[14]设f是复平面C上的超越亚纯函数,n是非负整数.如果fnP(f)=Q(f),且 deg Q≤n,其中 P,Q是 f 的微分多项式,它们的系数 a(z)满足 m(r,a)=S(r,f),则m(r,P(f))=S(r,f). 引理 2.3[15]设f是复平面C上的超越亚纯函数,满足m(r,f)=S(r,f).若 其中A0(z),A1(z),A2(z)为f的小函数. 引理 2.4设 n(≥3),k是正整数,a是非零常数,f是复平面 C上的亚纯函数,如果 f(k)+afn≠0,且f的极点重级至少为k+1,则f退化为常数. 由引理2.2知,m(r,H)=S(r,f). 由 f的极点重级 p≥k+1,得 2p≥p+k+1,再根据 (1)式中 f2的极点重级为 2p,φf(k)−f(k+1)的极点重级为p+k+1,可知f的极点不可能是H 的极点.因此H 的极点只能由g的零点产生,故N(r,H)=N(r,1/g)=0,于是就有T(r,H)=S(r,f). 将 (3),(4),(5)式代入(1)式,则有 比较左右两边,从而有 其中 Pi(φ),Qi(φ)是 φ 的 i次多项式,其系数 a(z)是 H,A1,A2的微分多项式,因而a(z)是f的小函数. 下面将f(k)及f(k+1)代入(1)式并整理,得 则 fh1=h2,易见 f的 k+1级极点不可能是h1的极点,由(2)式知,N(r,h1)=S(r,f),再由引理2.2知m(r,h1)=S(r,f),所以T(r,h1)=S(r,f),即h1是f的小函数. 现在分两种情形讨论. 情形 1h1≡0,则 h2≡0,所以 H ≡0,即有两边积分得f3=c(f(k)+f3),即cf(k)≡(1−c)f3. 若 c=1,则 f(k)≡0,f是次数至多为 k−1的多项式,这与条件 f(k)+af3≠0矛盾;若 c≠1,由于 f的极点重数 p≥k+1,则 p+k=3p,即 k=2p≥2k+2,即 k+2≤0,矛盾. 情形 2h1̸≡ 0,则于是有 于是就有T(r,f)=S(r,f),这对于非常数的f是不可能的,因此f是常数. 引理2.5[16-17]设n是正整数,b是非零常数,f是复平面C上的亚纯函数,如果fnf′≠b,那么f 是常数;进一步,如果f是超越的,那么fnf′取每个非零有限值无穷多次. 引理 2.6设n(≥3),k是正整数,a(≠0),b是两个有穷复数,F是区域D 内的一族亚纯函数,族中每个函数的极点重数至少为k+1.如果∀f∈F,有L(f)+afn≠b,则F 在区域D 内正规. 证明过程完全类似于参考文献[8]. 引理 2.7设(n≥3),k是正整数,a是非零有穷复数,f是复平面C上的非常数亚纯函数,若f的所有零点重级至少为k,极点重级至少为k+1,则f(k)(z)+afn(z)至少有两个判别零点. 证明假设f(k)(z)+afn(z)只有一个零点,以下分两种情形讨论. 情形 1当k≥2时,令 由 f的零点重级至少为 k知 f(k)̸≡0,所以 ψ(z)̸≡0.由 (8)式 ,得 由f的极点重级p≥k+1知,p+k=np,k=(n−1)p≥(n−1)(k+1),这是不可能的.所以f是整函数.于是 情形 2k=1时,令于是φ的零点重级≥2. 因为 只有一个零点,记为 ξ0,于是ξ0是φ的重级极点或者是φn−2φ′−a的零点. 若 φ 是非常数多项式,则 φn−2φ′−a=B(z− ξ0)l,其中 B 是非零常数,l是正整数,且l≥3. 由于 ψ 的零点重级 ≥ 4,ψ′的唯一零点 ξ0也是 ψ′的零点,故 ψ′(ξ0)=0,于是 a=0,这与a≠0矛盾.因此φ和ψ只能是非多项式的有理函数.设 其中 其中B是非常数,因此 其中h3也是多项式. 从 (15)-(17)式,可知 类似地,由(19),(20)式得 因此 m+t−i=3t,m=2t+i≠2t,从 (15)式可知,deg(h1)=s+t−1,则 deg(p1)=m+t−1,于是m+t−1=3t,即2t+1=m≤2t,矛盾. 证明不失一般性,设D=△={z:|z|≤1},任取z0∈D,下面证明F在z0处正规.∀f∈F分两种情况讨论. 情形 1L(f(z0))+afn(z0) ≠b 则 ∃ δ>0,使得 ∀z∈Dδ={z:|z−z0|< δ}有 L(f(z))+afn(z)≠b.于是 ∀h∈F,在 Dδ内有L(h(z))+ahn(z)≠b,则由引理2.6知,F 在Dδ内正规,于是 F 在 z0处正规. 情形 2L(f(z0))+afn(z0)=b.再分两种情形讨论. 情形 2.1L(f)+afn= b. 下证F在z0处正规. 假设F 在z0处不正规.由引理2.1知,∃{fj}⊂F,zj∈△,zj→z0,ρj→0+,使得 在复平面C 上按球距内闭一致收敛于g(ξ),其中g(ξ)是复平面C 上的非常数亚纯函数.因此 gj(ξ)在 C 上去掉 g的极点后的区域内内闭一致收敛于 g(ξ).显然g(ξ)的所有极点重级也至少是k+1,所以 在复平面C 去掉g的极点后的区域内内闭一致收敛于akg(k)(ξ)+agn(ξ). 若 akg(k)(ξ)+agn(ξ)≡ 0,设 ξ0是 g(ξ)的重级为 p的极点,p≥ k+1,则有 p+k=np,即k=(n−1)p.由p≥k+1知,k≥(n−1)(k+1),这是不可能的.所以g是整函数.于是有 即T(r,g)=S(r,g),这与g是非常数亚纯函数矛盾. 由条件∀f,h∈F,L(f)+afn与L(h)+ahn在区域D内分担b,知对于任意的正整数m,有 情形 2.2L(f)+afn≡b. 证明过程完全类似于情形2.1中akg(k)(ξ)+agn(ξ)≡0的情况. 综上所述,F在z0处正规,由z0的任意性可知,F在D内正规. [1]Hayman W K.Picard values of meromorphic functions and their derivatives[J].Annals of Mathematics,1959,5(3):28-32. [2]Hayman W K.Research Problems in Function Theory[M].London:Athione Press,1967. [3]庞学诚.微分多项式的正规定则[J].科学通报,1988,33:1690-1693. [4]Schwick W.Normality criteria for families of meromorphic functions[J].J.Analyse Mat.,1989,52:241-289. [5]Ye Y S,Pang X C.On the zeros of a di ff erential polynomial and normal families[J].J.Math.Anal.Appl.,1997,205(1):32-42. [6]Xu Y.Normal families of meromorphic functions[J].J.Math.Wuhan,2001,21:381-386. [7]雷春林,方明亮,杨德贵,等.关于Hayman问题与分担值[J].数学物理学报,2008(5):802-807. [8]叶亚盛.一个涉及极点重数的亚纯函数正规定则[J].上海理工大学学报,2007(3):265-267. [9]Schwick W.Sharing values and normality[J].Archiv der Mathematics,1992,59(1):50-54. [10]陈怀惠,顾永兴.Marty定则的改进及其应用[J].中国科学:A辑,1993,23(2):123-129. [11]仇惠玲,刘丹,方明亮.涉及正规族与分担值的Hayman问题[J].中国科学:数学,2012,42(6):603-610. [12]Pang X C,Zalcman L.Normal families and shared values[J].Bull London Math.Soc.,2000,32(3):325-331. [13]Zalcman L.Normal families:New perspectives[J].Bull Amer.Math.Soc.,1998,35:215-230. [14]Clunie J.On integral and meromorphic functions[J].J.London Math.Soc.,1962,37(1):17-27. [15]Steinmetz N.¨Uber die nullstellen von di ff erential polynomial[J].Math.Z.,1981,176(2):255-264. [16]Bergweiler W,Eremenko A.On the singularities of the inverse to a meromorphic function of fi nite order[J].Rev.Math.Iberoamericana.,1995,11(2):355-259. [17]陈怀惠,方明亮.关于fnf′的值分布[J].中国科学:A辑,1995(7):38-39. Normal criterion of meromorphic functions with multiple poles and shared values Lin Qiong,Ye Yasheng,Yu Weipeng This paper considers normality criteria for a family of meromorphic functions concerning multiple poles by the thought of sharing value,our results generalize the theorems of related papers and references. multiple poles,shared values,normal family O174.52 A 1008-5513(2017)03-0286-12 10.3969/j.issn.1008-5513.2017.03.008 2017-03-22. 国家自然科学基金(11371139). 林琼(1990-),硕士生,研究方向:基础数学. 2010 MSC:30D45







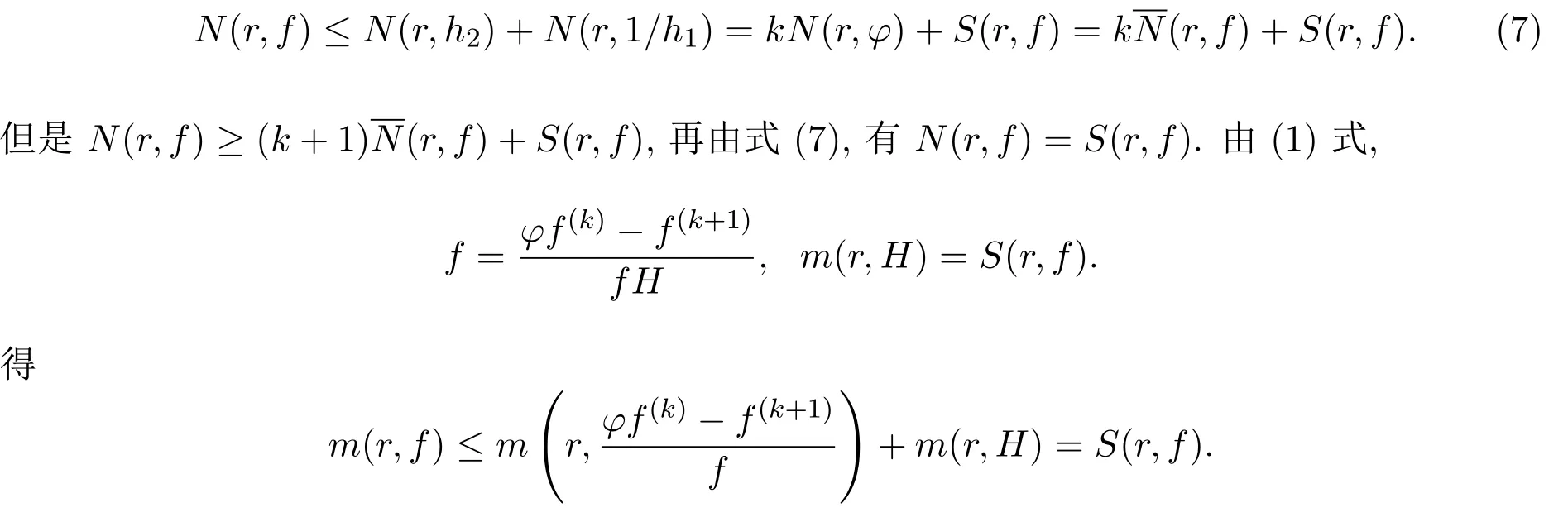



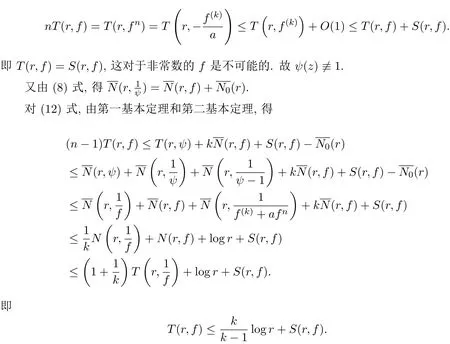

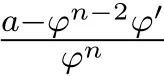

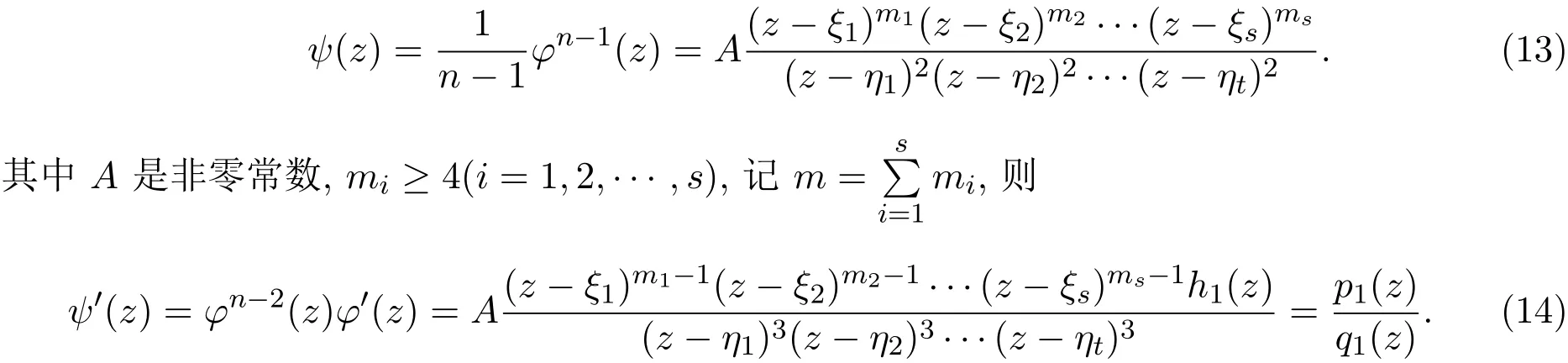
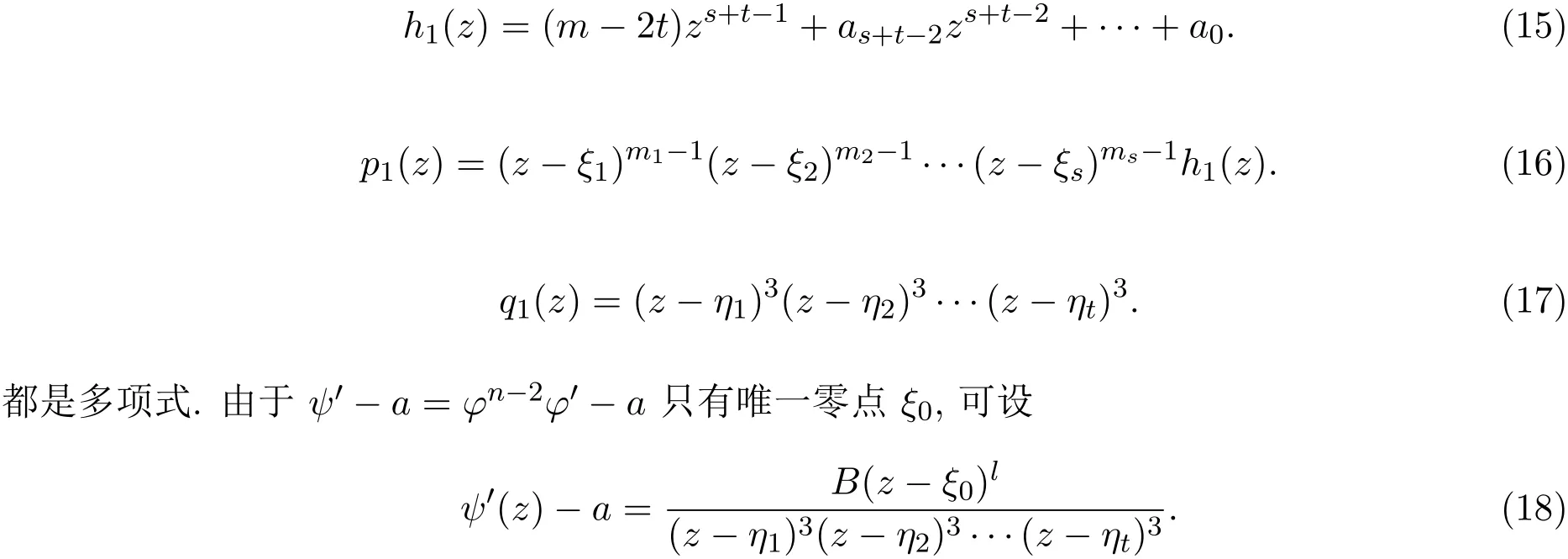
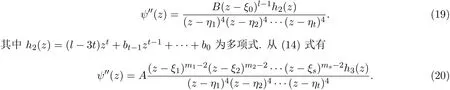
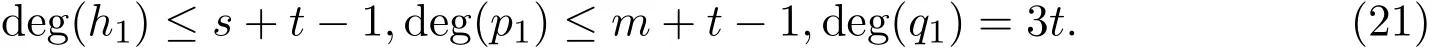

3 定理的证明
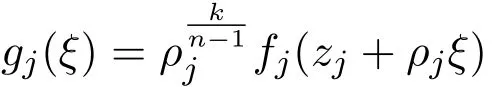
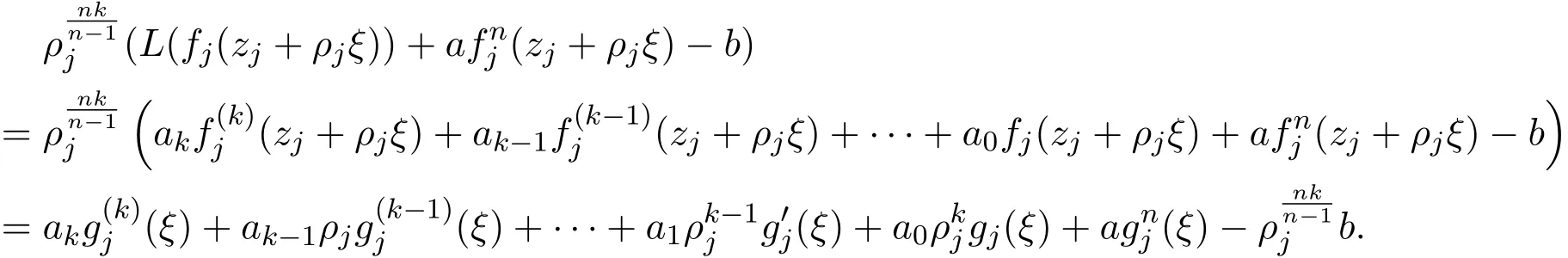


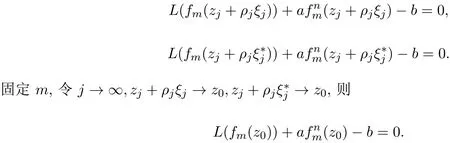
(College of Science,University of Shanghai for Science and Technology,Shanghai200093,China)
