垂直裂缝井椭圆流模型在F油田的应用
2017-07-12赵梓瑜尹洪军
赵梓瑜,尹洪军,王 磊
垂直裂缝井椭圆流模型在F油田的应用
赵梓瑜1,尹洪军1,王 磊2
(1.东北石油大学石油工程学院,黑龙江大庆 163318;2.大庆油田第二采油厂,黑龙江大庆 163711)
为了确定适合于F油田目前密井网生产条件的试井解释方法,统计分析了F油田的历年试井资料,总结试井曲线规律,根据试井资料曲线特征最终确定垂直裂缝井椭圆流模型适合该油田开发现状,并且给出了考虑注采比的密井网条件地层压力计算方法。以F油田A井为例,对该井关井162 h进行分析,实测曲线反映出了双线性流阶段,解释出的参数和计算出的地层压力与油井符合度较高。研究结果对F油田具有一定的实用性,可以为F油田制定下一步开发方案提供科学依据。
渗流力学;垂直裂缝井;密井网;试井解释;椭圆流;地层压力
油田在开发至一定阶段时,针对产能和渗透率降低等问题都会采用压裂技术对储层进行改造以提高油井产量。对于采用了压裂技术的油田,在开发过程中利用试井资料可以获得油田有关的动态参数,为油井压力动态分析提供可靠的依据。垂直裂缝井的试井分析技术是压裂井渗流理论研究的重要应用之一,国内外学者对此进行了许多研究。
垂直裂缝井的模型基本可分为3种:CINCO等[1]提出的平面二维模型,刘慈群[2]、RILEY等[3]提出的椭圆流模型,以及LEE等[4]提出的三线性流模型。刘慈群等[5-7]、尹洪军等[8]提出的椭圆流模型更符合实际地层渗流情况,并且通过平均质量守恒定律和扰动椭圆的概念求出了模型的近似解,使得计算结果更加简洁。张义堂等[9-10]对椭圆流模型的近似解进行了进一步研究,并在大量计算的基础上给出了修正方法。自此之后,许多学者在椭圆流模型的基础上进行了相关研究[11-16]。本文在文献[17—18]的基础上,给出了基于椭圆流模型的试井解释方法,以及适合于密井网生产条件下的地层压力计算方法,并将两种方法结合用于F油田,能够解释出可靠的地层参数用于地层压力评价,对于F油田制定下一步开发方案具有一定的参考价值。
1 F油田开发现状
F油田的中低渗透储层占有较大比例,因此油井投入生产后基本都采取压裂甚至重复压裂措施,随后历经弹性溶解气开发、注水开发、一次井网加密、二次井网加密、三次井网调整等5个大开发阶段。多次压裂和加密井网的设计部署,使得油水井的井距与排距逐渐缩小,井间干扰严重,致使地层流体渗流方式变得越来越复杂,而且部分井即使关井较长时间,压力恢复曲线也难以出现径向流直线段。目前,已有的地层压力计算方法,如MBH法[19]、Dietz法[20],已不再满足对F油田地层压力的计算、开发需要。为了解决存在的问题,本文开展了相关研究。
通过对该油田历年试井资料进行统计分析,发现共有4 300余井次可以解释,油井有3 800余井次,其中有3 750余井次的试井曲线表现为压裂井曲线特征,占总井数的98.7%。根据以上数据以及F油田压裂投产以及密井网部署的实际开发情况,决定采用垂直裂缝井椭圆流模型对F油田的试井资料进行解释,并利用曲皓[18]提出的裂缝性油藏线性流地层压力计算方法对F油田进行地层压力评价。根据垂直裂缝井模型的解可绘制出垂直裂缝井试井典型曲线,再利用典型曲线拟合试井解释方法即可获得渗透率、表皮系数等相关地层参数。最后,将相关参数代入到地层压力计算公式中即可得到单井控制范围内的平均地层压力。
2 理论基础
2.1 垂直裂缝井模型
垂直裂缝井不稳定渗流数学模型由两部分组成,即地层中的流动和裂缝中的流动。从地层角度来说,可将裂缝看成汇区;对于裂缝来说,内部流动一般看成一维流动。
1)地层椭圆流模型
控制方程为
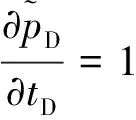
(1)
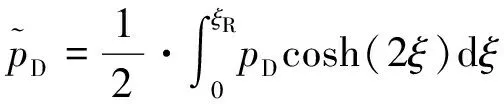
初始条件:
pD|tD=0=0 ,
(2)
内边界定产条件:

(3)
外边界封闭条件:
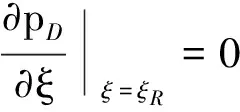
(4)
式中:ξ为椭圆坐标;pD为无因次压力;tD为无因次时间。
2)裂缝线性流模型
有限导流垂直裂缝井裂缝内的线性流控制方程为
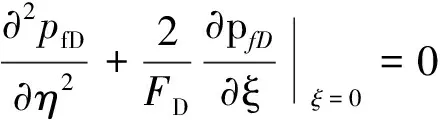
(5)
初始条件:
pfD|t=0=pD|t=0=0 ,
(6)
裂缝定产条件:
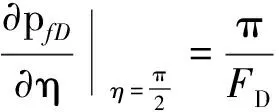
(7)
裂缝界面条件:
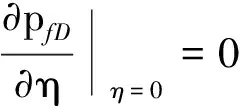
(8)
3)模型的解
有限导流裂缝井底压力公式为

(9)
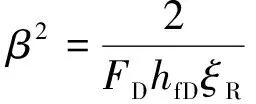
在Laplace空间利用Duhamel原理,引入无因次井筒存储系数CD和总表皮系数S,可得Laplace空间考虑井筒储集和裂缝表皮的无因次井底压力为
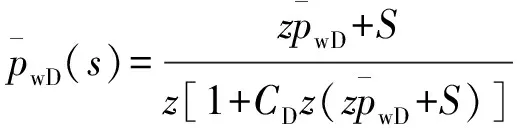
(10)
式中z为拉氏变量。
再根据Stethfest方法计算出井底压力的实空间解,通过该解即可绘制出垂直裂缝井的试井典型曲线。
2.2 密井网地层压力计算方法
控制方程:
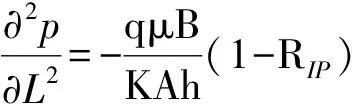
(11)
初始条件:
p(L,t=0)=pi,
(12)
内边界定产条件:
p(L=0,t)=pwf,
(13)
外边界封闭条件:
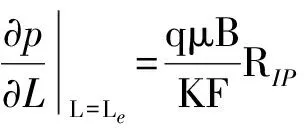
(14)
对上述数学模型求解并根据面积加权定义求得地层压力计算公式为

(15)
式中:pwf为井底流压,Pa;q为稳定产液量,m3/s;μ为流体黏度,Pa·s;B为流体体积系数;K为储层有效渗透率,m2;F为纵向泄油面积,m2;RIP为单井注采比;Le为供给边界到井底的距离,m。
结合前述的垂直裂缝井模型得到的典型试井曲线以及现场实测压力曲线,利用典型曲线拟合试井解释方法得到渗透率、表皮系数等参数,代入式(15)即可得到单井控制范围内的平均地层压力。
3 计算实例与讨论
3.1 计算实例
以F油田A井为例,关井162h进行压力恢复测试,压力恢复曲线表现出明显的压裂井曲线特征,测试的末点压力为1.16MPa,流压为0.24MPa,井径为0.1m。稳定生产期间,该井所在区块的注采比值为1.5,含水量为95.32%。A井其他基础参数见表1。利用垂直裂缝井椭圆流模型对A井关井恢复数据进行解释,压力恢复段如图1所示。

表1 A井基础参数
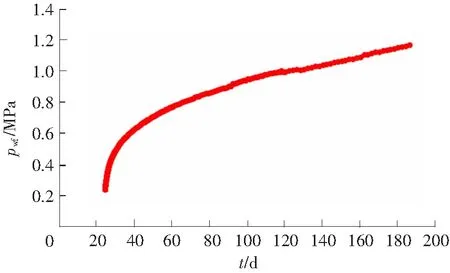
图1 A井压力史图Fig.1 Pressure history curve of well A
结合相关参数并利用典型曲线拟合试井解释方法分析压力恢复曲线,可得到储层参数:渗透率为9.469×10-3μm2,表皮系数为0.008。双对数拟合图如图2所示,拟合效果良好。将拟合得到的地层参数及其余参数代入式(15),得到该井控制范围内的平均地层压力为1.82 MPa。
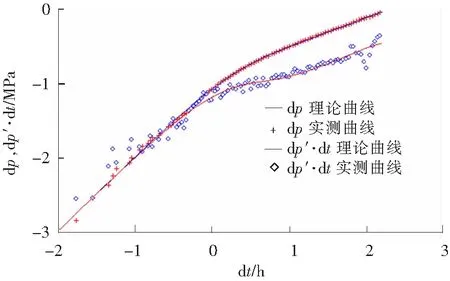
图2 A井双对数拟合曲线图Fig.2 Double logarithmic fitting curve of well A
3.2 讨论
从图2可知,实测曲线反映出了双线性流阶段,压力及导数曲线斜率为1/4。但因关井时间以及注采排距较小的影响,实测曲线并未反映出拟径向流阶段。该井计算压力与实际压力对比如表2所示。

表2 A井计算地层压力与实际地层压力对比
由表2可以看出,计算出的地层压力与实际地层压力较为接近,相对误差较小。再利用前文提出的试井解释方法对F油田的4 300余井次的压力恢复试井资料进行解释。表3给出了部分油井的试井解释结果,解释出的参数和计算出的地层压力与油田实际情况符合度达到92%以上。
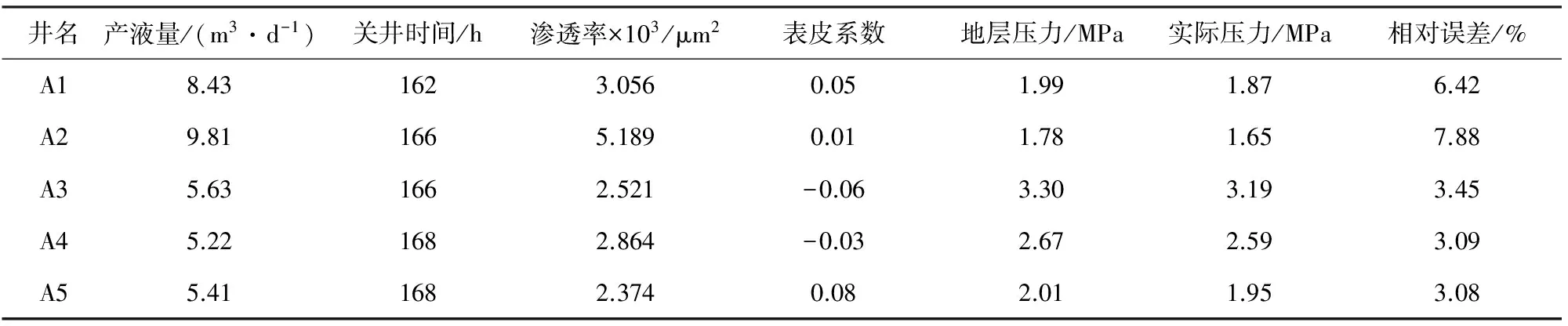
表3 F油田部分油井解释结果
以上计算结果表明,该解释方法对F油田有良好的适用性,解释计算结果可用于:1)定性分析生产井附近的储层特点;2)确定油层参数,分析井底附近污染状况和流体流动能力;3)利用平均压力评价单井压力水平。该方法对于油井后期如何配产、制定合理的工作制度以及油田整体开发方案的制定具有重要意义。
目前,F油田的试井解释仍存在两点问题:1)垂直裂缝井椭圆流模型对于少部分油井试井资料不适用;2)部分油井试井资料的参数缺失,无法解释。
未来还需要在以下3个方面展开深入研究。
1)对于少部分垂直裂缝井椭圆流模型不适用的油井,可以根据实测资料的曲线特征进行针对性分析,确定储层特点,采用合适的试井模型进行解释。
2)对试井资料参数缺失的油井,在无法补充、完善试井资料的情况下如何进行解释,将是今后研究的重点和难点。
3)F油田持续开发至一定阶段时,地层流体渗流方式改变,现有解释方法不再适用。因此,深入研究压裂井渗流理论具有重要的理论意义和实用价值。
4 结 语
根据F油田现场试井资料的曲线特征确定了适合当前开发情况的垂直裂缝井椭圆流试井模型和考虑注采比的密井网地层压力计算方法。通过实例分析以及大量的现场资料的计算结果可知,将这2种方法结合应用于F油田是可行的,能够解释出可靠的地层参数并进行准确的压力评价。本研究的结果可为F油田下一步开发方案的制定提供理论参考。
/References:
[1] CINCO H L, SAMANIEGO V F, DOMINGUEZ A N. Transient pressure behavior for a well with a finite-conductivity vertical fracture[J]. Society of Petroleum Engineers Journal, 1978, 18(4):253-264.
[2] 刘慈群. 垂直裂缝地层中流体的渗流[J]. 石油勘探与开发,1987(3):69-73. LIU Ciqun. The flow of fluid through porous media with a vertical fracture[J]. Petroleum Exploration and Development, 1987(3):69-73.
[3] RILEY M F, BRIGHAM W E, HORNE R N. Analytic solutions for elliptical finite-conductivity fractures[C]//SPE Annual Technical Conference and Exhibition. Dallas: Society of Petroleum Engineers, 1991:35-48.
[4] LEE S T, BROCKENBROUGH J. A new analytic solution for finite conductivity vertical fractures with real time and Laplace space parameter estimation[C]//SPE Annual Technical Conference and Exhibition. San Francisco: Society of Petroleum Engineers, 1983:103-106.
[5] 刘慈群. 在双重孔隙介质中有限导流垂直裂缝井的非牛顿流体试井分析方法[J]. 石油学报, 1990, 11(4):61-67. LIU Ciqun. Transient pressure behavior of a well with a vertical fracture with finite-conductivity in a reservoir with double-porosity[J]. Acta Petrolei Sinica, 1990, 11(4):61-67.
[6] 刘慈群, 杨玠. 垂直裂缝井非牛顿流体试井分析[J]. 石油钻采工艺, 1989(6):53-58. LIU Ciqun, YANG Jie. Well test analysis of non-newtonian fluid in vertical fractured well[J]. Oil Drilling & Production Technology, 1989(6):53-58.
[7] 刘慈群, 杨玠. 双重孔隙介质中垂直裂缝井的试井分析方法[J]. 石油勘探与开发, 1990(3):77-81. LIU Ciqun, YANG Jie. Analysis of transient test data for a well with a infinite conductivity vertical fracture[J]. Petroleum Exploration and Development, 1990(3):77-81.
[8] 尹洪军, 赵二猛, 王磊, 等. 考虑应力敏感的页岩气藏垂直裂缝井压力动态分析[J]. 水动力学研究与进展, 2015, 30(4):412-417. YIN Hongjun, ZHAO Ermeng, WANG Lei, et al. Pressure behavior analysis for vertical fractured well with stress sensitivity in shale gas reservoirs[J]. Chinese Journal of Hydrodynamics, 2015, 30(4):412-417.
[9] 张义堂, 刘慈群. 试井分析中椭园流模型近似解的实用化研究[J]. 油气井测试, 1996(2):19-21. ZHANG Yitang, LIU Ciqun. Practical study on approximate solution of elliptic flow model in well test analysis[J]. Well Testing, 1996(2):19-21.
[10]张义堂, 刘慈群. 垂直裂缝井椭圆流模型近似解的进一步研究[J]. 石油学报, 1996,17(4):71-77. ZHANG Yitang, LIU Ciqun. Further study on the approximate solutions of the elliptical flow model for wells with vertical fractures[J]. Acta Petrolei Sinica, 1996,17(4):71-77.
[11]刘曰武,刘慈群. 部分压开有限导流垂直裂缝井的试井分析新方法[J]. 油气井测试, 1997(2):13-16. LIU Yuewu, LIU Ciqun. New well testing analysis method for partially fractured well with finite conductivity[J]. Well Testing, 1997(2):13-16.
[12]刘曰武,刘慈群. 多层油藏有限导流垂直裂缝井试井方法研究[J]. 油气井测试, 1997(3):18-22. LIU Yuewu, LIU Ciqun. Well test method for vertically fractured wells in multilayered reservoir[J]. Well Testing, 1997(3):18-22.
[13]何应付, 徐联玉,吕万一, 等. 低渗透气藏压裂井产能分析[J]. 特种油气藏, 2006, 13(5):59-61. HE Yingfu, XU Lianyu, LYU Wanyi, et al. Productivity analysis of fractured well in low permeability gas reservoir[J]. Special Oil & Gas Reservoirs, 2006, 13(5):59-61.
[14]蔡明金, 贾永禄, 王永恒, 等. 低渗透双重介质油藏垂直裂缝井压力动态分析[J]. 石油学报, 2008, 29(5):723-726. CAI Mingjin, JIA Yonglu, WANG Yongheng, et al. Dynamic pressure analysis on wells with vertical fractures in low-permeability dual-porosity reservoir[J]. Acta Petrolei Sinica, 2008, 29(5):723-726.
[15]赵二猛, 尹洪军, 钟会影, 等. 三重介质油藏垂直裂缝井椭圆流试井模型研究[J]. 当代化工, 2015, 44(7):1654-1657. ZHAO Ermeng, YIN Hongjun, ZHONG Huiying, et al. Study on test model for vertical fractured well in triple media reservoir with elliptic flow[J]. Contemporary Chemical Industry, 2015, 44(7):1654-1657.
[16]马奎前, 郜益华, 孙召勃. 三重介质复合油藏椭圆流试井模型[J]. 断块油气田, 2017, 24(1):63-68. MA Kuiqian, GAO Yihua, SUN Zhaobo. Well test model of triple media composite reservoir based on elliptic flow[J]. Fault-Block Oil & Gas Field, 2017, 24(1):63-68.
[17]付春权, 尹洪军, 刘宇, 等. 低速非达西渗流垂直裂缝井试井分析[J]. 大庆石油地质与开发, 2007, 26(5):53-56. FU Chunquan, YIN Hongjun, LIU Yu, et al. Well testing analysis for vertical fracture wells with low-velocity non-Darcy flow[J]. Petroleum Geology & Oilfield Development in Daqing, 2007, 26(5):53-56.
[18]曲皓. 裂缝性油藏线性流地层压力计算方法[J]. 特种油气藏, 2015, 22(3):104-106. QU Hao. Calculation method of formation pressure in fractured reservoir featured by linear flow[J]. Special Oil & Gas Reservoirs, 2015, 22(3):104-106.
[19]MATTHEWS C S, BRONS F, HAZEBROEK P. A method for determination of average pressure in a bounded reservoir[J]. Society of Petroleum Engineers, 1954, 201(12):182-191.
[20]DIETZ D N. Determination of average reservoir pressure from build-up surveys[J]. Journal of Petroleum Technology, 1965, 17(8):955-959.
Application of vertical fractured well’s elliptical flow model in F oilfield
ZHAO Ziyu1, YIN Hongjun1, WANG Lei2
(1.College of Petroleum Engineering, Northeast Petroleum University, Daqing, Heilongjiang 163318, China; 2.No.2 Oil Production Plant, Daqing Oil Field Company, Daqing, Heilongjiang 163711, China)
In order to determine the well test interpretation method of dense well pattern which is applied to F oilfield, the well test data of F oilfield is counted and analyzed, and well test curve law is summarized. According to the curve characteristics of well test data, the ellipse flow model of vertical fractured well is determined, which is suitable for the development of the oilfield. Then, the calculation method of formation pressure for dense well pattern considering injection production ratio is given. Taking well A, F oilfield as example, it is analyzed after close for 162 h. The measured curve reflects double line flow stage, and the obtained parameters and calculated ground pressure better match with the well. It has a certain practicability to the F oilfield, and can provide a scientific basis for making the next development of F oilfield.
mechanics of flow through porous media; vertical fractured well; dense well pattern; well test interpretation; elliptic flow; formation pressure
1008-1534(2017)04-0265-05
2017-05-20;
2017-06-15;责任编辑:冯 民
黑龙江省自然科学基金(E2016015)
赵梓瑜(1993—),男,黑龙江大庆人,硕士研究生,主要从事油气渗流理论与应用方面的研究。
尹洪军教授。E-mail:yinhj7176@126.com
TE33
A
10.7535/hbgykj.2017yx04006
赵梓瑜,尹洪军,王 磊.垂直裂缝井椭圆流模型在F油田的应用[J].河北工业科技,2017,34(4):265-269. ZHAO Ziyu, YIN Hongjun, WANG Lei. Application of vertical fractured well’s elliptical flow model in F oilfield[J].Hebei Journal of Industrial Science and Technology,2017,34(4):265-269.
