生态文明建设评价指标体系及建模研究

李盼盼,冯爱芬,杜静娜

（河南科技大学数学与统计学院,河南洛阳471023）

生态文明建设评价指标体系及建模研究

李盼盼,冯爱芬,杜静娜

（河南科技大学数学与统计学院,河南洛阳471023）

加强生态文明建设是新常态经济下的重要要求.通过搜集生态文明建设评价指标体系的相关数据,选取森林覆盖率、自然保护区的有效保护等8项指标,构建生态文明建设评价指标体系,建立模糊综合评价模型,运用此模型对北京、上海、广东等10个省市的生态文明进行评价.结果显示：北京属于第一等级,上海、重庆属于第二等级,广东、湖南、云南、吉林属于第三等级,广西、新疆、河北属于第四等级.研究有利于各省市了解自身生态文明状况,从而不断完善生态文明建设,实现人与自然和谐发展.

生态文明；评价指标；主成分分析；熵值法

随着工业化和城市化进程的快速推进,我国城市生态环境问题日益突出,成为影响可持续发展的桎梏.党的十八大报告明确提出要大力推进生态文明建设,面对资源约束趋紧、环境污染严重、生态系统退化的严峻形势,必须树立尊重自然、顺应自然、保护自然的生态文明理念,把生态文明建设放在突出地位,努力建设美丽中国,实现中华民族永续发展.

关于生态文明的评价问题,目前国内已经有一些研究成果,蒋小平选取了生态环境保护、经济发展、社会进步3类20项指标构建了评价体系,并以河南省为例开展了实证研究[1]；杜宇等人提出了一种生态文明建设评价指标体系,运用综合指数法对我国2007年生态文明整体建设进程以及我国东中西部的6个省（市）的建设进程进行评价[2]；曹蕾进行了区域生态文明建设评价指标体系及建模研究[3].因生态文明指标较多,本文用模糊评价模型,对选取城市的生态文明进行排名.

1 生态文明建设评价指标体系构建

1.1 数据查询

通过查阅由北京林业大学生态文明研究中心、社会科学文献出版社联合发布的“生态文明绿皮书”《中国省域生态文明建设评价报告（ECI2014）》中《ECI2014设计与算法》部分,了解到了我国生态文明建设的评价模型[4].模型中对23项指标分别规定了各自的权重大小.具体数据见表1.

表1 生态文明建设评价指标体系（ECI2014）权重分配表Tab.1 The construction ofecologicalcivilization evaluation index system weightdistribution table（ECI2014）

生态文明指标体系的作用在于评价和比较各个区域的生态文明发展水平,因此与评价对象的界定指标体系直接相关.统计指标的选取是否合适,将直接影响评价的结论.但指标不是选取的越多越好,太多会使重复的指标相互干扰,太少则可能缺乏代表性.

国家发展改革委、财政部、国土资源部、水利部、农业部2013年12月共同制定了国家生态文明先行示范区建设评估参考指标库,并指出各建设地区可以结合本地区实际和主体功能定位要求,适当增减指标.本文在此指标库的基础上,结合蒋小平的研究,选取了生态环境保护、经济发展、社会进步3类20项指标构建了评价体系的相关研究,运用频度统计和相关性分析,筛选出高频指标,并将相关程度高的指标进行合并,并依照整体性原则、可操作性原则、定性指标与定量指标相结合的原则、相对独立性原则、可引导原则等5个原则,对指标进行整合,确定所研究的指标体系.

经过大量数据查询后,选取森林覆盖率、自然保护区的有效保护、城市生活垃圾无害化率、人均GDP、森林质量、建成区绿化覆盖率、城镇化率、每千人口医疗机构床位数这8个指标[5].从中国统计年鉴收集到全国从2004年到2014年上述8项指标数据,见表2.

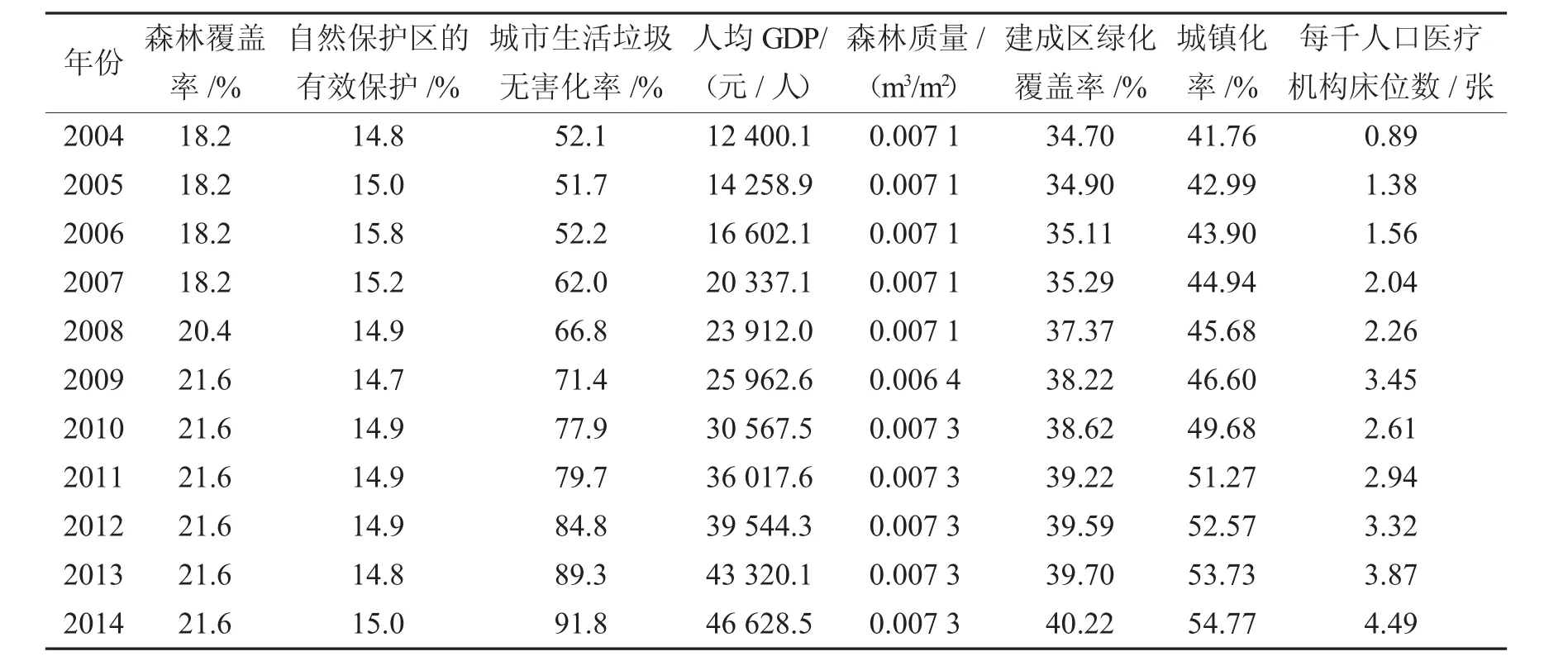
表2 2004年到2014年各项指标数据Tab.2 The indicatorsdata from 2004 to 2014

1.2 主成分分析

主成分分析是把原来的变量组合成一组新的互相无关的几个综合变量,同时根据需要从中取出几个较少的综合变量尽可能多的反映原来变量的统计方法.

因为未消除变量间数量级和量纲之间的不同,故先进行标准化处理,方式见公式（1）

式（1）中：Xij为实际变量值,Xi为各变量的算术平均值,Si为标准差,Zij为标准化后的变量值.对表2中的8个指标进行因子分析,经过标准化处理后得表3.

表3 2004年到2014年标准化处理后数据Tab.3 The standardized processing data from 2004 to2014

对标准化处理后的数据进行主成分分析法的KMO（检验统计量）指标和BXrtlett（巴特利球体）检验,KMO的度量值为0.701,BXrtlett的球形度检验P值为0,表明该样本适合主成分分析.然后利用SPSS求出特征值,可计算贡献率.

一般取累计贡献率达到85%～95%的特征值所对应的主成分,主成分分析表见表4.

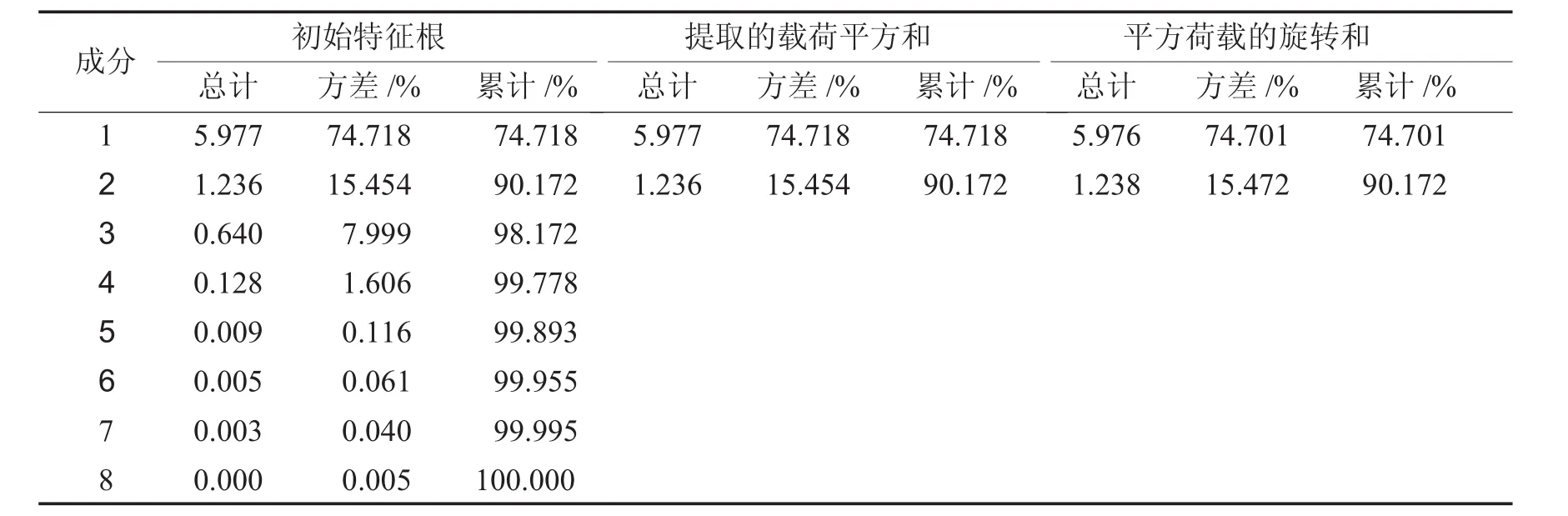
表4 主成分分析表Tab.4 Principalcomponentanalysis table

由表4可看出前两项成分的累计贡献率已达到了90.172%,所以提取前两项作为主成分.利用SPSS软件得出载荷矩阵,见表5.

表5 载荷矩阵Tab.5 The loadmatrix

计算生态文明建设两大主因子的得分值,将标准化后的原始数据矩阵与旋转后的载荷矩阵数据相乘,得到主因子得分矩阵,见表6.

表6 主因子得分矩阵Tab.6 Principal factor scoringmatrix

1.3 采用熵权法得指标权重

利用MATLAB程序得出两个主因子权重矩阵,见表7.

表7 主因子权重矩阵Tab.7 Principal factorweightingmatrix

旋转后的载荷矩阵和权重矩阵相乘,并归一化后便可得出各项指标的权重,见表8.

表8 各项指标的权重Tab.8 Weightofeach index

各指标权重的得出有利于清楚地看到该指标在整体评价中的相对重要程度,也为生态文明综合指数的计算提供了条件.

2 模糊综合评价模型

模糊综合评价方法是模糊数学中应用比较广泛的一种方法[6].在对某一事务进行评价时常会遇到这样一类问题,由于评价事务是由多方面的因素所决定的,因而要对每一因素进行评价；在对每一因素作出单独评语的基础上,如何考虑所有因素而作出一个综合评语,这就是一个综合评价问题.模糊综合评价就是先对单个因素进行评价,然后对所有因素进行综合模糊评价,防止遗漏任何统计信息和信息的中途损失.

2.1 模型的建立

建立模糊评价模型的具体步骤如下：

（1）运用相对隶属度函数对具有不同量纲和属性的各评价指标进行无量纲化,使处理后的各指标标准化值均处于[0,1]之间.相对隶属度函数,对于正指标

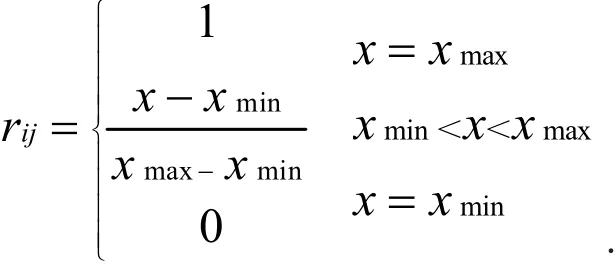
（2）得到模糊关系矩阵如下

（3）对数据进行归一化处理,根据生态文明建设评价指标的相对隶属度以及指标权重,使用加权求和法计算各个地区的生态文明综合评价总指数和各子系统评价指数（其中E为生态文明综合指数,Wi为各指标权重）.

（4）等级划分依据,参照米伟明的湘西地区生态文明建设研究,结合由北京林业大学生态文明研究中心、社会科学文献出版社联合主办的,由严耕教授带领的科研团队所写的《生态文明绿皮书：中国省域生态文明建设评价报告（ECI2014）》一书[4],将各省市生态文明指数进行等级划分,评语等级论域,即评语等级集合V{第一等级、第二等级、第三等级、第四等级}.依据各省市生态文明指数的平均值和标准差,将大于等于指数平均值和一倍标准差之和定为第一等级,将大于等于平均值但小于平均值与一倍标准差之和的列为第二等级,将小于一倍标准差的定为第四等级,其余列为第三等级[4].

2.2 模型应用

根据ECI2014数据,从属于社会发达型、均衡发展型、生态优势型、相对均衡型、环境优势型、低度均衡型6个类型的省市中挑选出10个具有代表性的省市,分别是北京、上海、广东、吉林、湖南、重庆、新疆、云南、河北和广西.并在国家统计局官网查找2014年的相关指标数据,对其进行数学模型应用,见表9.

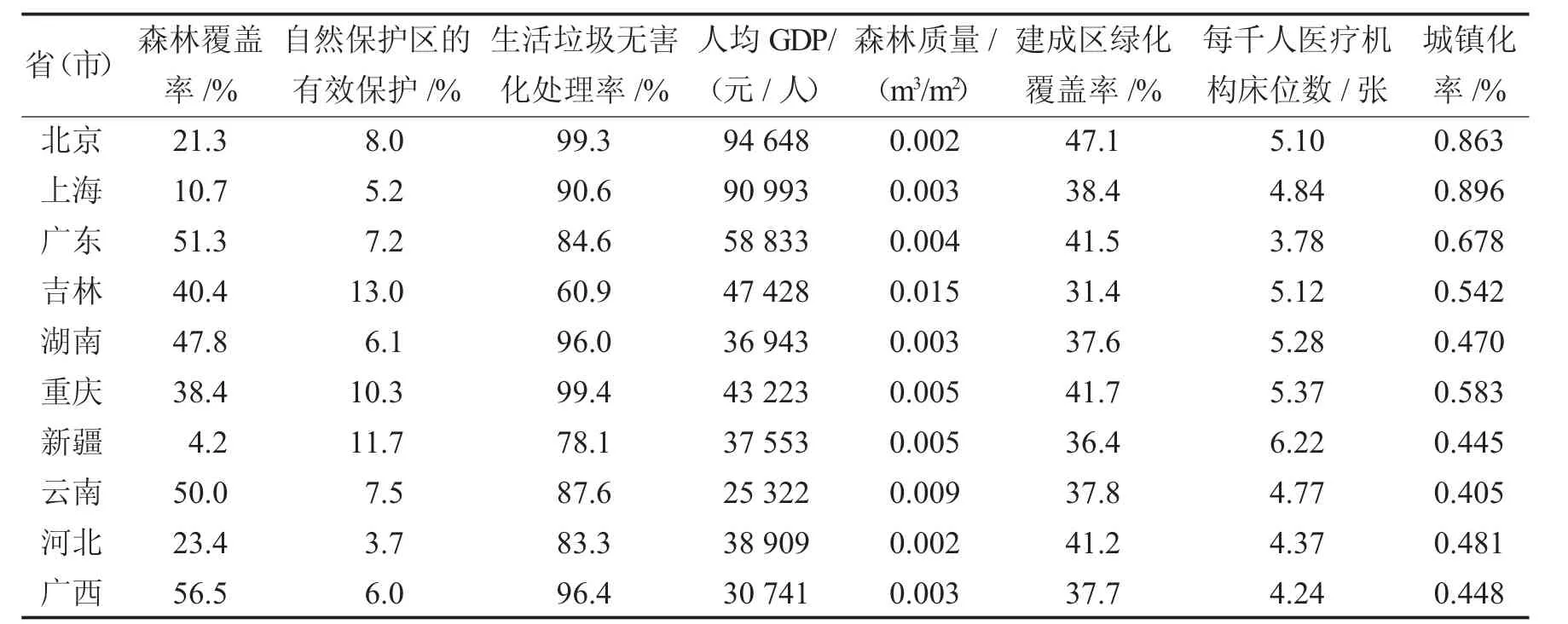
表9 2014年10个典型省（市）生态文明建设原始数据表Tab.9 Ten typicalprovince（city）tableoforiginaldata forecologicalcivilization construction in 2014

运用相对隶属函数对具有不同量纲和属性的各评价指标进行无量纲化,使处理后各指标标准化值均处于[0,1],得到矩阵R中的数据,见表10.

表10 各省（市）生态文明建设的标准化数据Tab.10 Standardized dataofecologicalcivilization construction in provinces

利用模型对城市进行生态文明等级划分[7],根据生态文明建设评价指标的隶属度以及指标权重,使用加权求和法,计算各个地区的生态文明综合评价总指数,在上述基础上利用MATLAB计算出各个城市的生态文明总指数W,见表11.

表11 城市的生态文明总指数Tab.11 The index ofecologicalcivilization city

依据评语等级的划分依据,计算生态文明指数的平均值和标准差的大小,各等级划分见表12.

表12 等级划分Tab.12 Division ofgrades

由表13可知,北京属于第一等级；上海、重庆属于第二等级；广东、湖南、云南、吉林属于第三等级；广西、新疆、河北属于第四等级.

3 小结

通过选取森林覆盖率、自然保护区的有效保护、森林质量、城市生活垃圾无害化率、人均GDP、建成区绿化覆盖率、城镇化率、每千人口医疗机构床位数这8项指标,运用主成分分析和熵权法,建立多层次模糊评价模型,对选取的北京、上海、广州等10个城市进行了相应的生态文明评价,得出如下结果：北京属于第一等级,上海、重庆属于第二等级,广东、湖南、云南、吉林属于第三等级,广西、新疆、河北属于第四等级.

预测结果能够较准确地反映该地区的生态文明建设情况.该模型具有较强的应用性和参考性.本文的研究成果有助于各省市及时对生态文明建设的影响因素进行调整和改进,构建更加宜居的生态环境.

[1]蒋小平.河南省生态文明评价指标体系的构建研究[J].河南农业大学学报,2008,42（1）：61-64.

[2]杜宇,刘俊昌.生态文明建设评价指标体系研究[J].科学管理研究,2009,27（3）：60-63.

[3]曹蕾.区域生态文明建设评价指标体系及建模研究[D].上海：华东师范大学,2014.

[4]严耕.生态文明绿皮书：中国省域生态文明建设评价报告（ECI2014）[M].北京：社会科学文献出版社,2014.

[5]米伟明.湘西地区生态文明建设研究[D].长沙：中南林业科技大学,2015.

[6]杨桂元,黄己立.数学建模[M].合肥：中国科学技术大学出版社,2008.

[7]魏晓双.中国省域生态文明建设评价研究[D].北京：北京林业大学,2013：18-85.

（责任编辑：卢奇）

App lication ofmathematicalmodeling in ecological civilization construction evaluation

LIPanpan,FENG AiFen,DU Jingna
（SchoolofMathematicsand Statistics,Henan University of Scienceand Technology, Luoyang 471023,China）

Strengthen ecological civilization is an important requirement under the new normal economy.Based on the collection of ecological civilization construction evaluation index system of relevant data,the forest coverage,the effective protection of natural reserves and other eight indicators was selected,the fuzzy comprehensive evaluation model was set up by constructing evaluation index system of ecological civilization construction in this paper.This modelwas used to evaluate the ecological civilization of ten provinces and cities,such as Beijing,Shanghai,Guangdong and so on,and the ecological civilization level of each province was obtained.The results showed that：Beijing belongs to the first rank；Shanghaiand Chongqing belong to the second grade；Guangdong,Hunan,Yunnan and Jilin belong to the third grade；Guangxi,Xinjiang and Hebei belong to the fourth grade.Conducive to the provinces and cities to understand their ecological civilization,so as to constantly improve the construction of ecological civilization to achieve harmonious development betweenman and nature.

ecological civilization；evaluation index；principal componentanalysis；entropymethod

O242.1 X821

A

1008-7516（2017）03-0050-07

10.3969/j.issn.1008-7516.2017.03.009

2017-05-02

国家自然科学基金（11301151）；河南省教育厅自然科学研究项目（13A110249）；河南科技大学创新团队项目（2015XTD010）；河南科技大学大学生研究训练计划项目（SRTP：2016080）

李盼盼（1996—）,女,河南驻马店人,本科生.

冯爱芬（1968—）,女,河南新安人,副教授,硕士生导师.主要从事图论与组合优化、数学规划研究.