数列部分的 高考复习策略

辽宁省实验中学　成建卓

近几年，《普通高等学校招生全国统一考试大纲的说明》中对数列部分的考试内容和要求具有严格的连续性，基本没有变化，且文科的要求和理科的要求完全一致。高考试题所涉及的数列问题完全符合《考试说明》中的考试内容和要求，题型新颖，难度适中。

《考试说明》中对数列部分的考试内容和要求是：

1.数列的概念和简单表示法

（1）了解数列的概念和几种简单的表示方法（列表、图像、通项公式）.

（2）了解数列是自变量为正整数的一类特殊函数.

2.等差数列、等比数列

（1）理解等差数列、等比数列的概念.

（2）掌握等差数列、等比数列的通项公式与前n项和公式.

（3）能在具体的问题情境中识别数列的等差关系或等比关系，并能用等差数列、等比数列的有关知识解决相关的问题.

（4）了解等差数列与一次函数的关系、等比数列与指数函数的关系.

从考试内容和要求中可以看出，在数列部分的复习中，重点是等差数列、等比数列的通项公式、前n项和、数列的求和方法，难点是在具体问题中识别数列的等差或等比关系，并能用等差数列或等比数列的有关知识解决相关问题.

一、等差数列和等比数列的性质及基本运算

不论是等差数列和等比数列的通项公式还是前 n 项和，都离不开 n、an、Sn、a1、d（q）这 5 个数学量的基本运算。

例1（2016年北京卷）已知an｛｝为等差数列，Sn为其前 n 项和，若 a1=6，a3+a5=0，则 S6=_____.

【解析】这个问题为简单问题，考查了等差中项的概念，等差数列的通项公式及前n项和公式.

易知 a4=0，从而 d=-2，S6=6.

例2（2016年全国Ⅰ卷）设等比数列an｛｝满足a1+a3=10，a2+a4=5，则 a1a2…an的最大值为 _____.

【解析】这个问题具有综合性，为中等难度的问题，考查了等比数列的通项公式、简单的二次函数最值问题.

故a1a2…an的最大值为64.

对于等差数列和等比数列的性质，复习的重点是等差中项和等比中项.

例3（2014年广东卷）若等比数列an｛｝的各项均为正数，且a10a11+a9a12=2e5，则lna1+lna2+…+lna20=_____.

【解析】本题考查了等比数列的性质以及对数的运算，为中等难度问题.

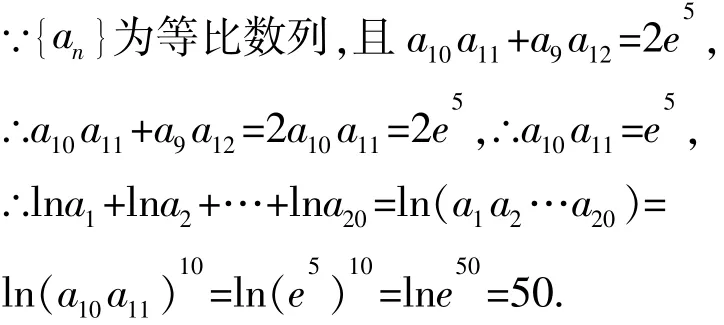
二、数列的求和方法

数列的求和方法一般可分为四种，即运用等差、等比数列的公式求和，倒序相加的方法，裂项法求和及错项相减的方法.

倒序相加的方法源自于教材中等差数列前n项和的推导，这个方法充分结合了等差数列的性质：若m+n=p+q则am+an=ap+aq.

例4已知一个项数为n的等差数列的前4项和为7，末4项和为33，这n项的和为100，求项数n.

【解析】由已知得

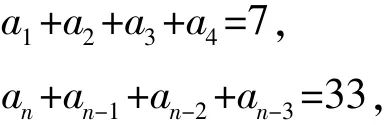
以上两式相加并根据等差数列的性质可得：

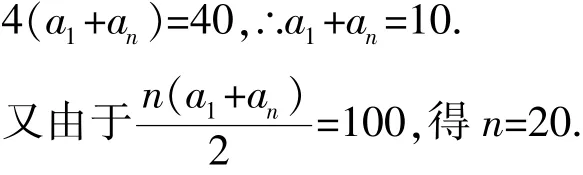
需要注意的是，末4项的和的倒序与前4项和的正序是解决问题的关键.

对于裂项法求和，现在高考的重点主要针对由等差数列构成的数列，即一类通项为分式，分母为一个等差数列相邻2项（或3项）的积，分子为常数的数列.

例5（2016年天津卷）已知｛an｝是各项均为正数的等差数列，公差为d，对任意的n∈N*，bn是an和an+1的等比中项.

求证：

所以｛cn｝为等差数列.

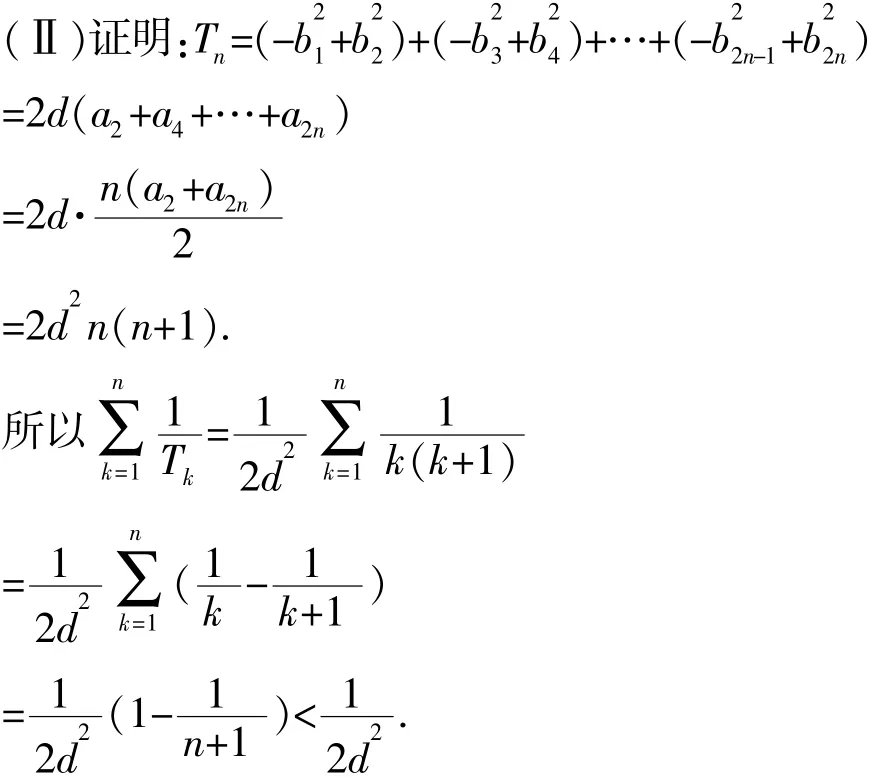
需要注意的是，裂项法求和所适用的数列不仅局限于通项公式是分母为一个等差数列相邻2项（或3项）的积，分子为常数的数列.在具体问题中，只要对通项可以进行裂项，且求和时可以逐项消去即可.比如例6.

例6数列｛an｝中，，则S=na1+a2+…+an=_____.

【解析】这个数列与等差数列并没有关系，但分母作积的两项之差刚好是分子，这是可以实施裂项的关键.

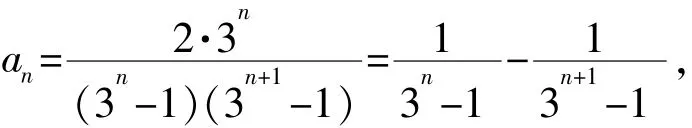
于是Sn=a1+a2+…+an

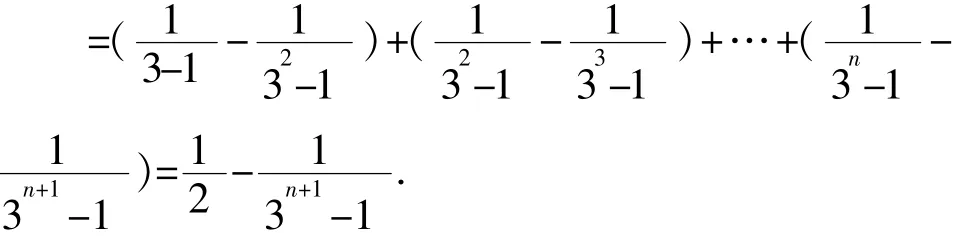
错项相减的方法源自于教材中等比数列前n项和的推导，这样数列的特征为通项是一个等差数列第n项和一个等比数列第n项的积.

例7（2016年山东卷）已知数列｛an｝的前n项和Sn=3n2+8n，｛bn｝是等差数列，且an=bn+bn+1.

（Ⅰ）求数列｛bn｝的通项公式；

【解析】（Ⅰ）由题意知当n≥2时，

an=Sn-Sn-1=6n+5，

当 n=1时，a1=S1=11，

所以an=6n+5.

设数列｛bn｝的公差为d.

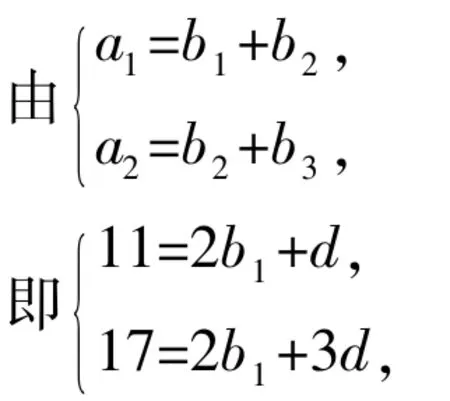
可解得b1=4，d=3.

所以bn=3n+1.

又Tn=c1+c2+…+cn，

得 Tn=3× ［2×22+3×23+…+（n+1）×2n+1］，

2Tn=3× ［2×23+3×24+…+（n+1）×2n+2］，

两式作差，得

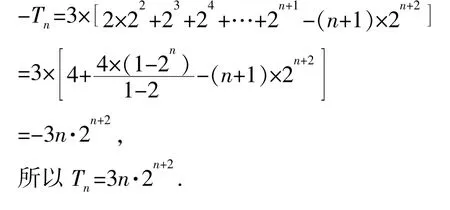
三、运用数列的知识解决相关问题

例8（2016年上海卷）无穷数列｛an｝由k个不同的数组成，Sn为an｛｝的前n项和.若对任意n∈N*，Sn∈2，3｛｝，则k的最大值为_____.

【解析】这是一个以数列为背景的考查数列的概念和数学思维能力的问题，属于中等难度的问题.

注意到题目的已知条件：若对任意n∈N*，Sn∈2，3｛｝，其中，“若对任意的n∈N*”为本题的关键词.

n=1时，a1=2或 3；

n=2时，可构造数列 2，0或 3，0或 2，1等；

n=3 时，可构造数列 2，1，0 或 2，1，-1 等；

n≥4时，由Sn=2或 3，得Sn-1=2或 3，其中 n≥2，于是 an=0.

故存在m∈N*，当n=m时，am=0，

即该数列从第4项开始均为0，可由n=3的情况构造数列，如

2，1，0，……或 2，1，-1，0……等均满足情况，所以k的最大值为4.

例9（2016年浙江卷）设数列an｛｝的前n项和为 Sn.若 S2=4，an+1=2Sn+1，n∈N*，则 a1=_____，S5=_____.

【解析】本题考查在具体的问题情境中识别数列的等差或等比关系，并能用等差数列或等比数列的有关知识解决相关问题，属于中等难度的问题.

由已知，a2=2a1+1，a1+a2=4，可解得 a1=1，a2=3.

又an+1=2Sn+1，

故有 an=2Sn-1+1（n≥2），

上述两式相减得an+1=3an

故数列是以1为首项，3为公比的等比数列，易得S5=121.

在数列部分的复习中，要严格依据《课程标准》和《考试说明》，对于数列的递推关系，教材中为选学内容，《考试说明》中要求较低.故对于数列的递推关系的复习要控制难度.