动态条件下电磁轨道炮膛内磁场和电场分析

殷强， 张合, 李豪杰

(南京理工大学 智能弹药技术国防重点学科实验室， 江苏 南京 210094)



动态条件下电磁轨道炮膛内磁场和电场分析

殷强， 张合, 李豪杰

(南京理工大学 智能弹药技术国防重点学科实验室， 江苏 南京 210094)

针对动态条件下电磁轨道炮膛内磁场和电场分布特性研究缺乏的问题，提出一种数值计算方法。基于磁扩散方程和安培定律，利用测得的动态实验数据和炮尾处磁通密度值，通过有限元计算，确定电枢区域和导轨区域的电流密度值；进一步计算得到电枢前端及后端中轴线各考察点磁场和电场分布特性。结果表明：随着与电枢距离的增加，各考察点峰值磁通密度逐渐减小，电枢前端各点衰减速度远大于后端各点；炮口时刻各考察点峰值电场值为膛内发射过程的数倍。提出的方法能够有效计算轨道炮智能炮弹部位感应电场和磁场，计算结果有助于智能炮弹电磁屏蔽设计。

兵器科学与技术； 电磁轨道炮； 电流密度； 磁通密度； 电场强度

0 引言

电磁轨道发射是一种能够将物体加速至超高速的新型发射方式，它利用电磁力驱动有效载荷，将电磁能转换成机械动能，可加速包括弹丸、炮弹、导弹、卫星、飞机等在内的多种物体[1-4]。为了实现精确打击并扩大杀伤效能，国内外已开始研究利用电磁轨道炮发射含有控制模块的智能炮弹替换动能弹[5-7]。由轨道炮的原理可知，强电流在导轨和电枢内部流动，会在膛内智能炮弹部位产生感应电场和磁场，这将对控制模块中的电子元器件产生电磁干扰，为了更好地进行电磁屏蔽设计，有必要先对电磁发射过程中智能炮弹部位感应电场和磁场的分布情况进行分析。

目前大部分商用有限元软件无法进行非时谐条件下运动系统的电磁场仿真，针对这一问题，本文提出一种数值计算方法，该方法利用文献[13]中的轨道炮动态实验数据，基于磁扩散方程和安培定律，通过有限元仿真得到电枢区域电流密度值，将导轨电流简化为沿表面分布的面电流，通过与炮尾考察点磁通密度实测值进行对比，确定导轨各表面电流密度值，利用毕奥- 萨伐尔定律和法拉第感应定律，计算得到动态条件下电枢前端和后端考察点磁场和电场分布特性，研究结果为轨道炮智能炮弹的电磁屏蔽设计提供依据。

1 计算模型和方法

1.1 计算模型

电磁轨道炮原理图如图1(a)所示，高功率脉冲电流I由一侧导轨流入，流经电枢后，从另一侧导轨流出，脉冲电流在炮膛内产生强磁场B，与电枢电流作用，产生洛伦兹力F推动电枢运动。假设输入电流在轨道炮高度h上平均分布，建立如图1(b)所示轨道炮二维计算模型，导轨为铝合金材料，长度为3 m，高度h为25 mm，宽度w为20 mm，导轨间距s为25 mm；电枢材料为铜合金，高度与导轨相等，长度L0为17.4 mm[14]。

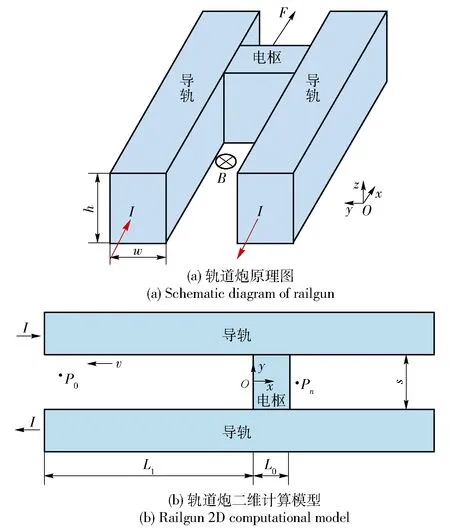
图1 轨道炮原理图及二维模型Fig.1 Schematic diagram and 2D model of railgun

如图1(b)所示，电枢受到电磁力作用，向右侧炮口方向移动。考虑到智能炮弹在膛内随电枢运动，二者之间相对静止，为了计算方便，定义电枢静止，导轨以速度v沿着-x方向移动[15]。以电枢后端面中心点为坐标原点，电枢长度方向为x轴，两导轨间距方向为y轴，导轨高度方向为z轴，建立图1中的系统坐标系，Pn代表考察点，位于电枢前端或后端中心轴线上，发射初始时刻电枢到炮尾距离L1为175 mm，此距离大于4倍口径，确保电枢接通电流时获得最大的推力。P0为炮尾部导轨间的磁场测量点，到炮尾距离为10 mm，到上导轨距离s1为10 mm，轨道炮炮尾位置的侧视图和P0点示意图见图2所示。

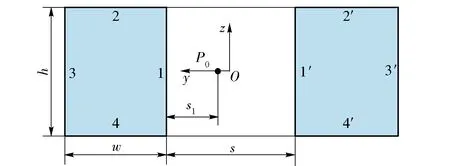
图2 轨道炮侧视图及P0点示意图Fig.2 Side view of railgun and diagram of P0

1.2 计算方法

在本文计算中，忽略导轨和电枢之间高速运动造成的导轨烧蚀等非线性作用，由于电磁轨道炮发射系统的尺寸远小于电磁场的波长，因此可以忽略位移电流，将轨道炮作为准静态系统进行研究[16-17]，麦克斯韦方程的微分形式[18]为

(1)

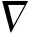
(2)

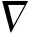
(3)

式中：H为磁场强度；J为电流密度；E为电场强度；B为磁通密度。

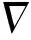
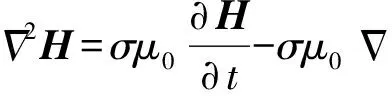
(4)

式中：σ和μ0分别为导体的电导率和真空磁导率；v为导体运动速度。在轨道炮二维计算模型中，主要存在z方向磁通密度Bz，系统模型中不存在铁磁性导体，且电导率和磁导率都与时间t无关，用Bz替代H，代入(4)式，可以得到二维模型中导体的磁扩散方程为

(5)

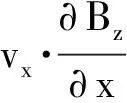
(6)

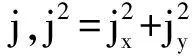
(7)

利用毕奥- 萨伐尔定律可以求得考察点位置的磁通密度值为

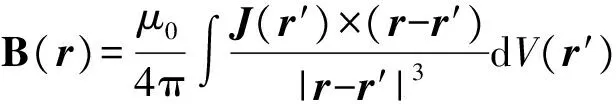
(8)

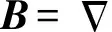
(9)

E=-∂A/∂t.

(10)

2 膛内磁场与电场计算

2.1 导轨及电枢电流分布计算

动态实验测量结果如图3所示：从速度曲线可以看出，电枢出膛时刻约为3.5 ms，炮口初速为1 400 m/s；从电流波形可以看出，电流幅值为710 kA，脉宽接近1 ms，3.5 ms后电流没有立刻下降到0，这是由于电枢出膛后较大的电弧电阻续流导致的；从炮口电压波形可以看出，电压值在3.5 ms时陡然增大到530 V，这是较大的电弧电阻压降导致的[19]，同时也表明电枢在这一时刻出膛。电弧在炮口形成之后，炮口电压经历了非常不稳定的行为，并且随着剩留磁能的持续释放而逐渐下降。

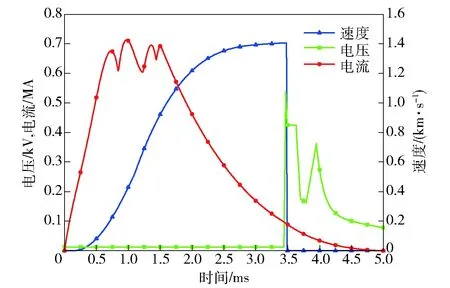
图3 动态实验测量结果Fig.3 Measured results of dynamic experiment

由于导轨和电枢关于Oxz平面对称，可以选取一半区域作为研究对象。边界条件如图4所示，S1表示导轨后端区域，S2表示电枢与导轨接触区域，S3表示电枢区域，电枢和导轨内部初始磁感应强度值Bz=0，当电枢相对导轨高速滑动时引起速度趋肤效应,会使得磁场与电流集中在导轨内侧边缘与电枢后边缘，因此设置边界条件Bz=μ0j′，j′是电流线密度[20]，j′=I/h，I为轨道炮输入电流，导轨左侧边界设置为无限长，∂Bz/∂x=0，电枢中部边界∂Bz/∂y=0，其他各边界设置为Bz=0[21]。

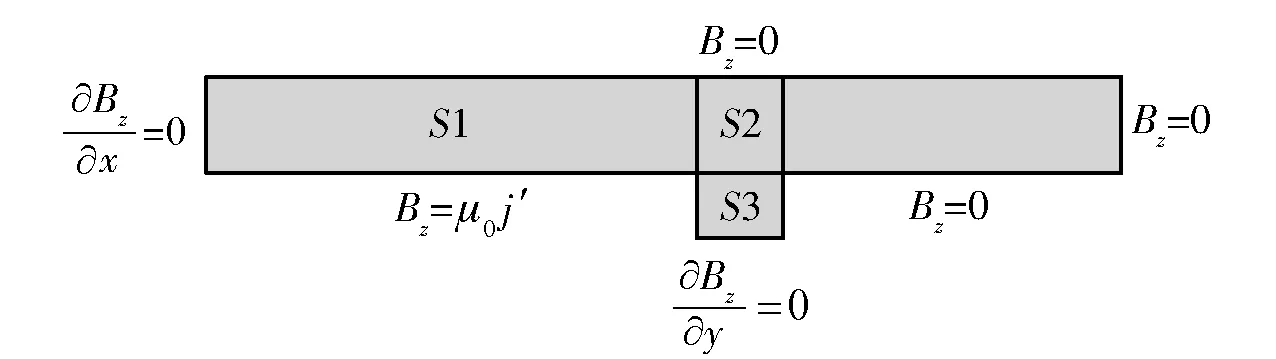
图4 边界条件示意图Fig.4 Schematic diagram of boundary conditions

将图3中动态实验测得的各时刻输入电流值和电枢速度，结合导轨和电枢区域的边界条件和初始值，利用有限元仿真软件COMSOL Multiphysics 4.4中的PDE模块，对导轨和电枢区域的磁扩散方程进行求解，得到不同时刻各个点的磁通密度值，再利用(7)式可以计算得到导轨和电枢区域的电流密度值。由麦克斯韦方程可以证明，电流不能穿越连续的磁感应强度等值线，因此磁感应强度等值线可以被认为是电流的流线图，显示电流流通的路径。选取0.25 ms、1.20 ms和3.10 ms时刻的磁通密度分布来对电流的流通情况进行分析，如图5所示，由于速度趋肤效应，电流沿着导轨后端(S1区域)表面分布，且速度越大，趋肤深度越小[22]，电流仅从电枢尾部与导轨接触的狭小区域流入电枢并扩散开来。通过比较图5中各个时刻的磁通密度分布可以发现，速度趋肤效应对导轨中的电流分布有很大影响，但对电枢内部电流分布范围的影响不大，导轨和电枢接触区域(S2区域)的大部分基本没有电流通过。从文献[23]中的电流分布图可以得到类似结论。

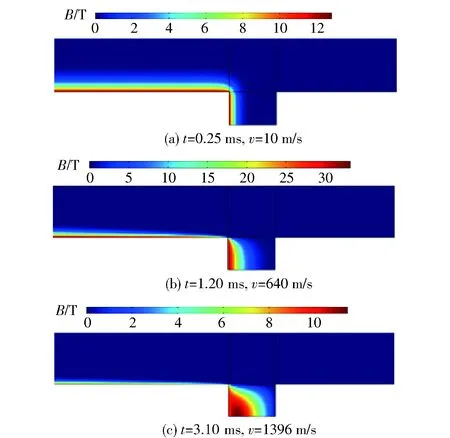
图5 0.25 ms、1.20 ms和3.10 ms时的磁通密度分布图Fig.5 Contours of magnetic flux densities at 0.25 ms, 1.20 ms and 3.10 ms

图4设置的边界条件假设导轨外侧电流分布为0，事实上，由于发射过程中普遍存在电流趋肤效应，导轨的4个表面(即平面1～平面4及各自相对应平面1′～平面4′，见图2)都有电流分布，电流的趋肤深度很小，可以简化为无厚度的电流平面进行分析[24]。导轨平面1(平面1′)和平面3(平面3′)上电流大小分别为C1hI/2(h+w)和C2hI/2(h+w)，平面2、平面4、平面2′和平面4′上电流大小为wI/2(h+w)，C1和C2为电流分布系数，用来表示速度趋肤效应和电流邻近效应对电流分布的影响，通常C1>C2，且C1+C2=2[25]，两侧导轨对应表面流经的电流大小相等，方向相反。

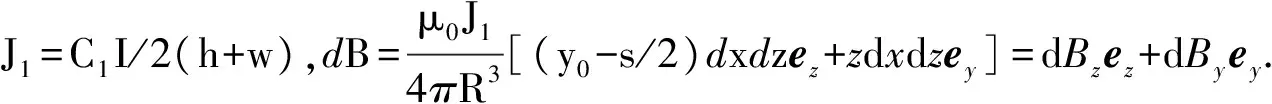
简单分析可得，面1在P0点只产生-z方向磁场，取d1=s/2-y0，则Bz的表达式为

(11)

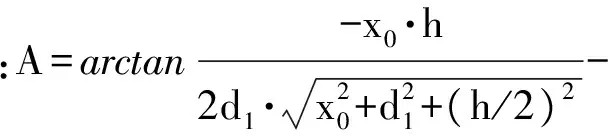
经过计算可知，(11)式中A的计算值随着电枢运动距离L的变化而逐渐增加，但增加幅值逐渐减小，最终稳定在1.48. 因此(11)式可以表示为Bz=-C1hI/2(h+w)×2.96×10-7.

同理可以计算得到平面1′、平面3和平面3′在P0点产生的磁通密度值。对于平面2和平面4以及对应另一侧导轨上的平面2′和平面4′，它们在P0点产生的y方向磁场相互抵消，产生-z方向磁场大小相等，方向相同，可以一并计算。由此可以发现，两侧导轨各面在测量点位置均产生-z方向磁场，可以将它们的叠加值用含有C1和C2及轨道尺寸、电流等参数进行表达。

对于电枢来说，由于电枢初始位置距离测量点P0大于4倍口径，且随着电枢与P0相对距离迅速增加，可以忽略电枢电流对P0磁场的影响，考虑C1∶C2分别为1∶1、3∶1、5∶1、7∶1、9∶1 5种情况，计算整个导轨电流在P0产生磁场的总和，与实测值进行对比，各种不同条件下P0点磁通密度模如图6所示。

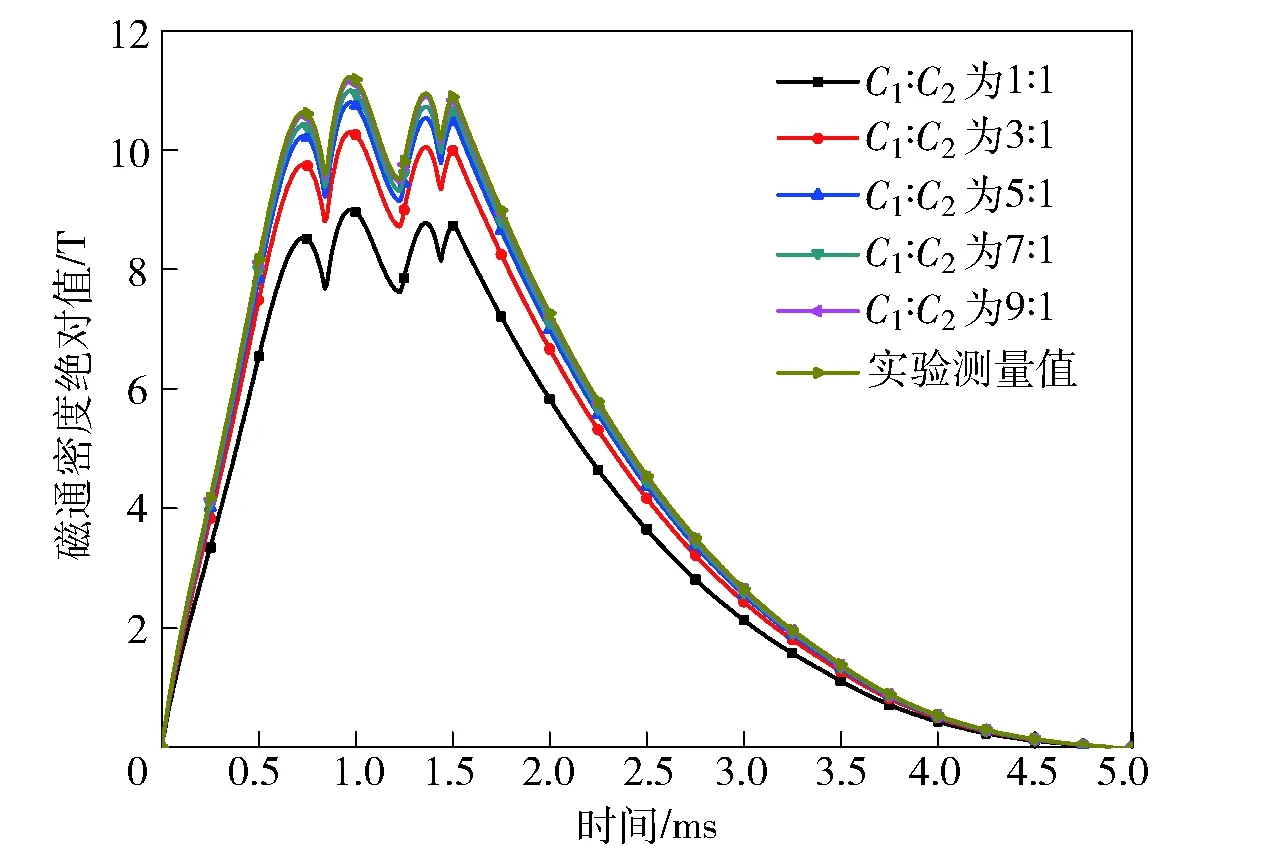
图6 不同比值下P0点磁通密度值和实验测量值Fig.6 Measured and calculated magnetic flux density values of P0 under different ratios

由图6中可以看出：当C1∶C2为1∶1时，P0点峰值磁通密度比其他条件下都小，只有9T；随着C1∶C2的不断增加，导轨电流在P0点产生的磁通密度逐渐增加，当C1∶C2为9∶1，即C1=1.8，C2=0.2时，计算值与实测值基本符合，为11T. 根据前面的计算表达式可以得到两侧导轨上各个面的电流密度值。

图7所示为导轨各面及电枢内部电流密度绝对值，时间为0～3.5 ms，即电枢在膛内运动的时刻，Jay和Jax分别表示电枢内部-y方向和x方向体电流密度值，单位为A/m2.Jay的波形与输入电流波形相似，最大值为1.9×109A/m2；Jax从起始时刻开始缓慢增加，在1.75 ms左右达到最大值6×108A/m2，随后逐渐下降。导轨各面面电流密度单位为A/m，J1表示导轨平面1及平面1′的电流密度值，最大值为1.4×107A/m，J2表示平面2、平面2′、平面4和平面4′的电流密度值，J3表示平面3及平面3′的电流密度值。

11月6日，全球第一大矿业集团公司——必和必拓（BHP）与中农集团控股股份有限公司签订了氯化钾合作备忘录，约定自BHP位于加拿大的钾矿项目Jason投产之后，每年通过中农控股向中国市场销售氯化钾。

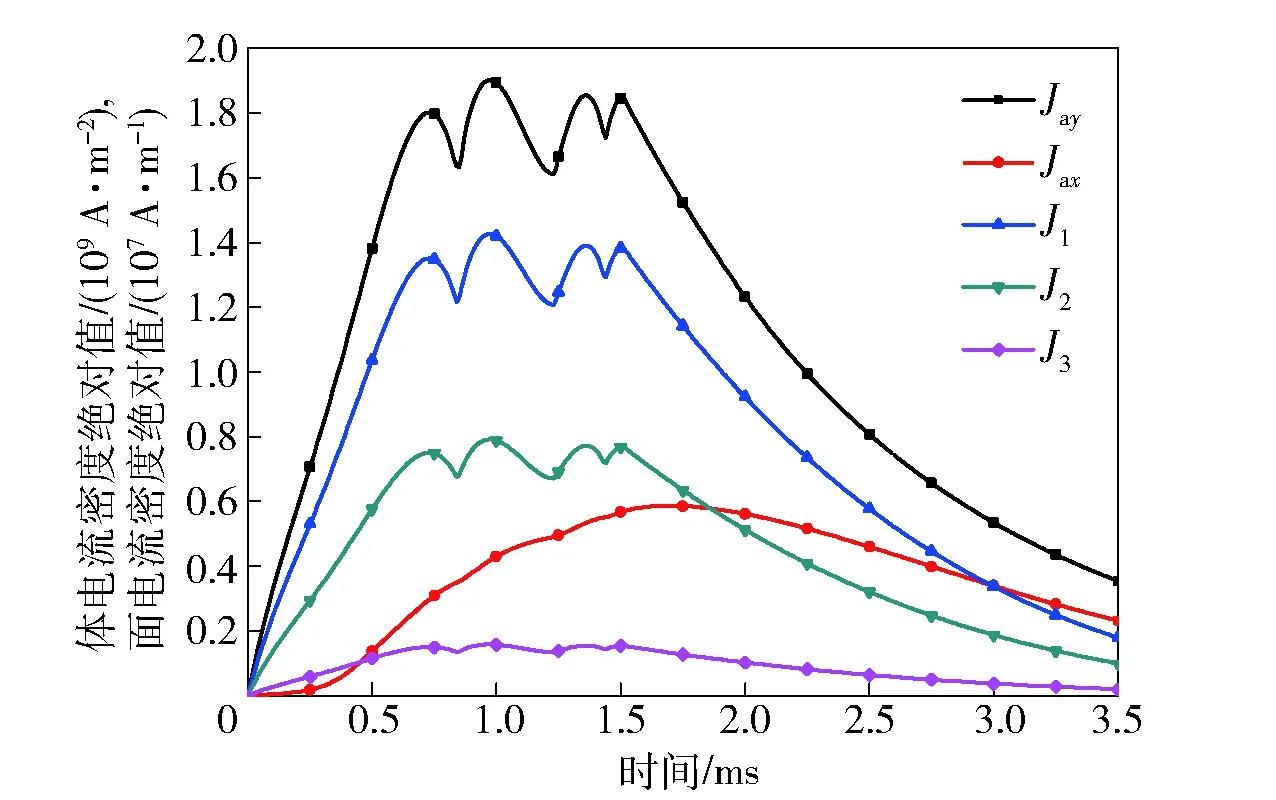
图7 导轨各面及电枢电流密度绝对值Fig.7 Absolute values of current densities in armature and each surface of rail

2.2 膛内磁场计算

考虑到各类型智能炮弹控制模块所处位置不同，分别在x轴上的电枢前端和后端取3点进行考察，考察点坐标分别为P1(-0.01 m,0,0)、P2(-0.03 m,0,0)、P3(-0.05 m,0,0)、P4(0.027 4 m,0,0)、P5(0.047 4 m,0,0)、P6(0.067 4 m,0,0)，它们到电枢的距离分别为10 mm、30 mm和50 mm.

导轨各表面电流在各考察点均产生-z方向磁通密度，计算方法见前文介绍，这里主要分析电枢电流产生的磁场。由图1可知，流经电枢关于x轴对称区域的x方向电流大小相等，方向相反。简单分析可知，它们在考察点产生的y方向磁场刚好抵消。产生-z方向磁场大小相等，方向相同。电枢y方向电流在电枢后端考察点(P1～P3)产生-z方向磁场，在电枢前端考察点(P4～P6)产生+z方向磁场。以电枢y方向电流为例，计算在考察点Pn(d, 0, 0)产生的磁场(d为考察点到坐标原点的轴向距离)。对于电枢区域来说，电流元为

Idl=-Jaydxdydzey，R=(d-x)ex-yey-zez，

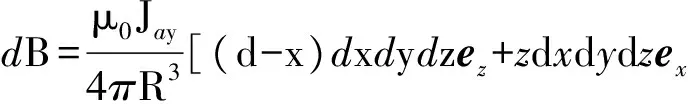
简单计算可知，Bx=0，

(12)

分别计算流经电枢和导轨电流在考察点位置产生的磁通密度，进行叠加计算，可以发现，电枢后端各考察点只存在-z方向磁通密度，前端各考察点只存在z方向磁通密度，各考察点磁通密度绝对值如图8所示。

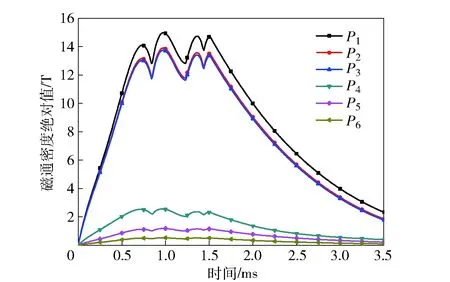
图8 各考察点磁通密度绝对值Fig.8 Absolute values of magnetic flux densities of investigated points

从图8中可以看出：电枢后端各点P1、P2、P3峰值分别为15T、14T和13.7T，电枢前端各点峰值远小于后端各点，P4、P5、P6各点峰值分别为2.56T、1.18T和0.52T；随着与电枢距离的增加，考察点磁通密度峰值逐渐减小，电枢前端各点衰减速度明显大于电枢后端各点；对于电枢后端P1和P2点，从15T到14T，只衰减了6.7%；电枢前端P4和P5点，从2.56T到1.18T. 衰减率达到54%. 产生以上现象的原因有:1)导轨位置电流对电枢后端区域产生的磁通密度远大于对电枢前端区域产生的作用; 2)电枢电流和导轨电流在电枢后端产生的磁通密度方向相同，相互叠加而减小了空间衰减作用。

2.3 膛内电场计算

(13)

由(10)式可得

(14)

用J′ay表示Jay对时间t的导数，通过观察图7中的Jay波形图可以发现，Jay在0.75～1 ms间存在多个上升或下降的阶段，因此J′ay在零值附近多次变向。为了简化分析过程，取J′ay最大值进行分析。简单计算可知，J′ay在0.86 ms时刻有最大值5.56×1012A/(m2·s)，取电枢前端各考察点到坐标原点的轴向距离d从18 mm到65 mm，得到各点峰值电场Ey如图9所示。

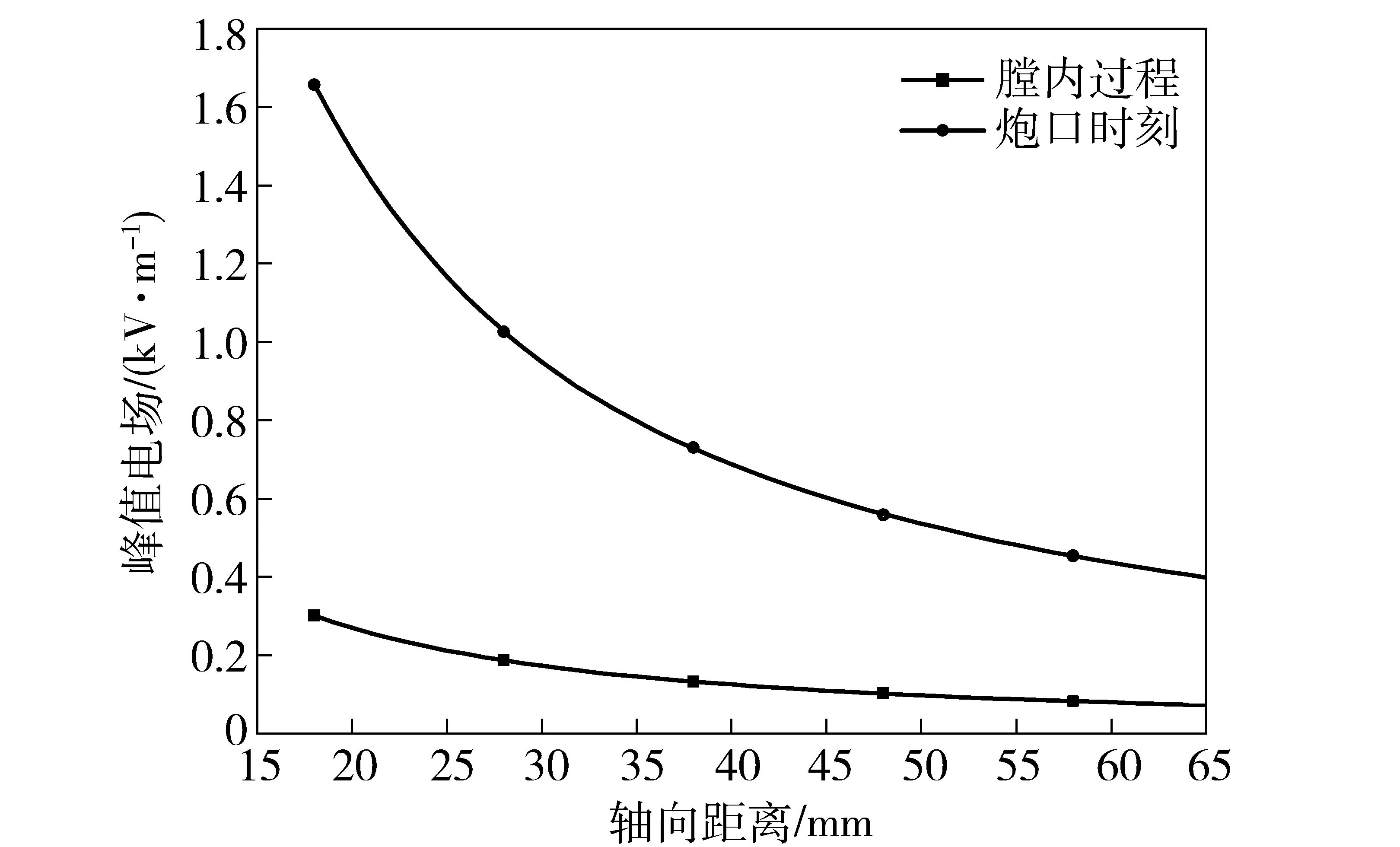
图9 各考察点峰值EyFig.9 Peak values of Ey of investigated points

从图9可以看出，电枢前端各考察点峰值电场逐渐减小，从300 V/m下降到75 V/m.

3 分析

3.1 炮口电场计算

前面计算的考察点电场处在膛内发射过程中，当电枢出炮口瞬间，电枢电流迅速降为0，将在考察点位置产生较大的感应电场。结合图7中Jay值在出膛时刻为3.8×108A/m2，长度为17.4 mm的电枢以1 400 m/s速度运动时间为1.24×10-5s，计算得出膛时刻J′ay为3.06×1013A/(m2·s)，对各个考察点产生的感应电场约为膛内运动时刻的5.5倍，如图9所示，峰值电场从1 655 V/m到400 V/m.

3.2 导轨内外侧电流密度比值对膛内磁场影响

由图5可知，电枢运动速度越大，导轨的电流趋肤深度越小，导轨内外侧电流密度比C1∶C2越大，表1为不同内外侧电流密度比条件下各考察点位置的峰值磁通密度。

表1 不同内外侧电流密度比下各点峰值磁通密度

Tab.1 Peak magnetic flux density values of investigated points under the condition of different ratios ofC1∶C2T

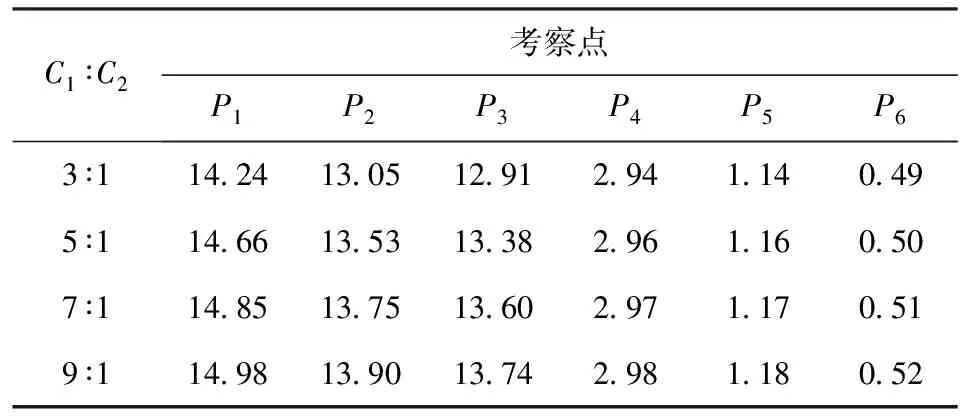
由表1可以看出，随着C1∶C2的增加，各考察点峰值磁通密度模呈现逐渐增大趋势，对比电枢后端各点P1～P3与前端各点P4～P6，可以发现，导轨内外侧电流密度比的变化对电枢后端区域磁通密度的影响大于电枢前端区域。

4 结论

本文通过建立轨道炮二维计算模型，利用动态实验数据，基于磁扩散方程和安培定律，通过有限元仿真得到电枢区域电流密度，将导轨电流简化为沿表面分布的面电流，得到不同内外侧电流比值条件下炮尾考察点的磁通密度计算值，经过与考察点实测值对比，确定导轨各表面电流密度值。在此基础上，进一步计算得到电枢前端及后端各考察点磁场和电场分布情况，并对炮口电场和导轨不同内外侧电流密度比值条件下考察点磁通密度进行分析，得到以下结论：

1) 电枢后端考察点峰值磁通密度远大于电枢前端各点，随着与电枢之间距离的增加，考察点峰值磁通密度逐渐减小，电枢前端考察点峰值磁通密度衰减速度明显大于电枢后端考察点。应将智能炮弹控制模块安装于离电枢较远的前端位置。

2) 电枢前端各考察点，与电枢距离越大，峰值感应电场越小，出炮口瞬间，由于电枢电流迅速降为0，将产生数倍于膛内发射过程的强电场。应注意进行炮口位置强电场屏蔽。

3) 在输入电流一定的情况下，电枢运动速度越大，电枢前端及后端考察点峰值磁通密度越大，但电枢后端考察点峰值磁通密度变化明显大于电枢前端各点。

References)

[1] Marshall R A, Wang Y. Railguns: their science and technology[M]. Beijing: China Machine Press, 2004: 1-6.

[2] 李军, 严萍, 袁伟群. 电磁轨道炮发射技术的发展与现状[J]. 高电压技术, 2014, 40(4): 1052-1064. LI Jun, YAN Ping, YUAN Wei-qun. Electromagnetic gun technology and its development[J]. High Voltage Engineering, 2014, 40(4): 1052-1064.(in Chinese)

[3] Xu L Z, Geng Y B. Forces of rails for electromagnetic railguns[J]. Applied Mathematical Modelling, 2012,36(4): 1465-1476.

[4] 张亚舟, 李贞晓, 金涌, 等. 电磁发射用13MJ脉冲功率电源系统研究[J]. 兵工学报, 2016, 37(5): 778-784. ZHANG Ya-zhou, LI Zhen-xiao, JIN Yong, et al. Research and development on a 13 MJ pulsed power supply for electromagnetic launcher[J]. Acta Armamen-tarii, 2016, 37(5): 778-784.(in Chinese)

[5] Luciano M. Development and testing of high explosive (HE) projectiles for electro-magnetic gun[C]∥40th Aunnual Armament Systems: Guns-Ammunition-Rockets-Missles Conference and Exhibition. New Orleans, LA, US: NDIA, 2005: 25-28.

[6] Ciolini R, Schneider M, Tellini B. The use of electronic components in railgun projectiles[J]. IEEE Transactions on Magnetics, 2009, 45(1): 578-583.

[7] McNab I R, Stefani F. Development of a naval railgun[J]. IEEE Transactions on Magnetics, 2005, 41(1): 206-210.

[8] Zielinski A, Le C D, et al. In-bore electric and magnetic field environment[J]. IEEE Transactions on Magnetics, 1999, 35(1): 457-462.

[9] Levinson S, Erengil M, Faust J, et al. Evaluation of magnetic shields for instrumented launch packages, IAT.R 0265[R]. Austin, TX, US: Institute for Advanced Technology, The University of Texas at Austin, 2002.

[10] 殷强, 张合, 李豪杰, 等. 静止条件下轨道炮膛内磁场分布特性分析[J]. 强激光与粒子束, 2016, 28(2):174-179. YIN Qiang, ZHANG He, LI Hao-jie, et al. Analysis of railgun in-bore magnetic field distribution at zero speed[J]. High Power Laser and Particle Beams, 2016, 28(2): 174-179.(in Chinese)

[11] Cobum W, Le C, et al. Electromagnetic field measurements near a railgun[J]. IEEE Transactions on Magnetics, 1995, 31(1): 698-703.

[12] Cao R G, Li J, Jiao Q J, et al. Measure variation of magnetic field waveforms above rails of a railgun during launching period[J]. IEEE Transactions on Plasma Science, 2013, 41(5): 1475-1478.

[15] Young F J, Hughes W F. Rail and armature current distributions in electromagnetic launchers[J]. IEEE Transactions on Magnetics, 1982, 18(1): 33-41.

[16] 林庆华, 栗保明. 电磁轨道炮三维瞬态涡流场的有限元建模与仿真[J]. 兵工学报, 2009, 30(9): 1159-1163. LIN Qing-hua, LI Bao-ming. Finite element analysis of 3D transient eddy field in electromagnetic railgun[J]. Acta Armamen-tarii, 2009, 30(9): 1159-1163.(in Chinese)

[17] Cobum W, Williams W. Static and quasi-static models for the magnetic field of a railgun[J]. IEEE Transactions on Magnetics, 1995, 31(1): 692-697.

[18] 雷银照. 电磁场[M]. 北京: 高等教育出版社, 2008: 133-137. LEI Yin-zhao. Electromagnetic field[M]. Beijing: Higher Education Press, 2008: 133-137.(in Chinese)

[19] 石江波, 栗保明. 电磁轨道炮后坐过程研究[J]. 兵工学报, 2015, 36(2): 227-233. SHI Jiang-bo, LI Bao-ming. Research on recoil process of electromagnetic railgun[J]. Acta Armamentarii, 2015, 36(2): 227-233.(in Chinese)

[20] 李军. 电磁轨道炮中的电流线密度与膛压[J]. 高电压技术, 2014, 40(4): 1104-1109. LI Jun. Linear current density and bore pressure of electromagnetic railgun[J]. High Voltage Engineering, 2014, 40(4): 1104-1109.(in Chinese)

[21] Li X, Weng C S. Three-dimensional investigation of velocity skin effect in U-shaped solid armature[J]. Progress in Natural Science, 2008, 31(1): 698-703.

[22] 杨玉东, 王建新, 薛文. 轨道炮动态负载特性的分析与仿真[J]. 兵工学报, 2010, 31(8): 1026-1031. YANG Yu-dong, WANG Jian-xin, XUE Wen. Simulation and analysis for dynamic load characteristic of rail-gun[J]. Acta Armamentarii, 2010, 31(8): 1026-1031.(in Chinese)

[23] Long G C, Weldon W F. Limits to the velocity of solid armatures in railguns[J]. IEEE Transactions on Magnetics, 1989, 25(1): 347-352.

[24] Keshtkar A, Maleki T, Kalantamia A, et al. Determination of optimum rails dimensions in railgun by Lagrange’s equations[J]. IEEE Transactions on Magnetics, 2009, 45(1): 594-597.

[25] 聂建新, 韩晶晶, 焦清介, 等. 电磁轨道发射器的几何尺寸对电感梯度的影响[J]. 高电压技术, 2010, 36(3): 728-732. NIE Jian-xin, HAN Jing-jing, JIAO Qing-jie, et al.Effect of rail-type electromagnetic launcher dimensions on inductance gradient[J]. High Voltage Engineering, 2010, 36(3): 728-732.(in Chinese)

Analysis of In-bore Magnetic and Electric Fields in ElectromagneticRailgun under Dynamic Condition

YIN Qiang， ZHANG He， LI Hao-jie

(Misterial Key Laboratory of ZNDY, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)

A numerical computation method is presented for the distribution characteristics of in-bore magnetic and electric fields in electromagnetic railgun under dynamic condition. The measured dynamic test data and the magnetic flux density at the breech end of the railgun are used to calculate the current densities in the armature and rails based on the magnetic diffusion equation and Ampere’s law. The distribution characteristics of magnetic field and electric field of the investigated points along the central axes of the armature front end and back end are calculated. The results show that the peak magnetic flux densities of each investigated point decrease gradually with the increase in the distance from point to armature, the decay rate of the investigated point in front of the armature is much larger than that the point behind the armature. The electric field intensity of the investigated point at the muzzle is about several times of that in in-bore launching process. The proposed method can effectively calculate the induced electric field and magnetic field of railgun intelligent ammunition. The calculated results can be used in the electromagnetic shielding design of intelligent ammunition.

ordnance science and technology; electromagnetic railgun; current density; magnetic flux density; electric field intensity

2016-09-19

武器装备预先研究项目(9140C300106150C30001)

殷强(1988—), 男, 博士研究生。 E-mail: xtsxwbyinqiang@163.com

张合(1957—), 男, 教授, 博士生导师。 E-mail: hezhangz@njust.edu.cn

10.3969/j.issn.1000-1093.2017.06.003

TJ012.1+5; TM153+.1

A

1000-1093(2017)06-1059-08