t-Copula-GARCH模型在沪深市场联动风险测算中的应用研究——基于拟蒙特卡罗模拟方法

刘 新，王福豪

(重庆理工大学 经济金融学院， 重庆 400054)



t-Copula-GARCH模型在沪深市场联动风险测算中的应用研究
——基于拟蒙特卡罗模拟方法

刘 新，王福豪

(重庆理工大学 经济金融学院， 重庆 400054)

为测算沪深两市联动风险，以上证指数和深证成指收益率数据为研究对象。首先，根据Copula建模思想，利用GARCH(1,1)-t模型拟合沪深市场波动特征，利用t-Copula函数拟合沪深市场联动风险特征。进而利用拟蒙特卡罗方法模拟沪深股指组合未来收益率序列，测算沪深市场联动风险。实证结果表明：拟蒙特卡罗方法收敛速率快，模拟结果的精确性和稳定性较好。拟蒙特卡罗方法表现出的优势可以帮助机构投资者有效管理市场风险，这对于机构投资者做出科学投资决策具有深远意义。

机构投资者；联动风险；Copula建模；拟蒙特卡罗模拟

伴随当前一系列“黑天鹅”事件的发生，全球金融市场风险呈现出了新特征。金融市场风险复杂多变的特征又增加了投资机构对金融市场风险管理的难度。金融相关性分析是市场风险管理的关键问题。目前，在金融相关性分析领域，Copula理论发展较为成熟。根据Copula理论的建模思想，可以用Copula函数和各个风险因子的边缘分布计算多个风险因子的联合分布，在联合分布的基础上，计算多金融时间序列的在险价值，这为金融市场联动风险测算提供了新的建模方法。

一、文献综述

Sklar于1959年首先提出Copula理论，并且指出，可以将一个联合分布分解成K个边缘分布和一个Copula函数,边缘分布用来刻画单项金融时间序列的变动情况，Copula函数理论上可以描述多变量金融时间序列的相关模式[1]。为推广Copula理论，中外学者在理论和应用层面做出了诸多探讨。其中Bouye等给出多元正态Copula函数形式和多元t-Copula函数形式[2]，这两种分布函数形式都具有对称性特征，但是t-Copula函数形式具有更厚的尾部，对多元资产序列的尾部相关性变化比较敏感，特别是能够更好地刻画金融市场的尾部相关性。随着研究的不断深入，Copula函数与ARCH类模型的结合成为研究投资组合风险的主要模型。Engle于1982年提出自回归条件异方差(ARCH)模型用来刻画金融时间序列的时变性和集聚特征[3]。Bollerslev于1986年将ARCH模型推广为GARCH模型[4]。ARCH模型和GARCH模型的重要区别在于前者体现出金融时间序列的短期记忆性，而后者体现出金融时间序列的长期记忆性。

国内张尧庭引入Copula函数应用于金融风险分析并且称其为连接函数[5]，同时探讨了应该选择什么相关性指标度量金融风险。张明恒利用混合分布和Copula连接函数，给出风险价值的Copula计量模型和计算方法[6]。韦艳华等建立Copula-GARCH-t模型对上海股市各版块指数收益率的条件相关关系进行分析，结果表明沪市各版块之间存在很强的正相关关系，并且具有时变特征[7]。张自然等利用Copula模型研究人民币汇率境内SPOT市场、境内DF市场和境外NDF市场之间的相依关系[8]。谢赤等建立Copula模型分析汇改后人民币兑美元、欧元和日元汇率的相关关系，得出人民币兑欧元与兑日元汇率存在正相关关系，具有金融传染性特征[9]。高波等利用时变Copula建模方法分析不同市场的流动性相关关系，以研究系统流动性风险，结果表明t-Copula函数可以较好地描述不同市场流动性相关关系，回购市场对系统流动性风险的贡献高于同业拆借市场[10]。欧阳资生等利用Frank Copula函数研究信用利差与市场风险的相依结构，得出了较好的结果[11]。

综合以上国内外文献，作为一种新兴的多变量金融时间序列建模方法，Copula理论得到了相对完善的发展，t-Copula函数可以较好地刻画金融市场联动特征的尾部变化，GARCH-t模型可以较好地拟合金融时间序列的高峰厚尾、波动聚类和长记忆性等非线性特征。由此，为应对“黑天鹅”事件对我国机构投资者管理沪深市场联动风险能力的挑战， 论文利用t-Copula-GARCH模型描述沪深金融市场联动风险特征，进而利用随机模拟方法测算沪深市场联动风险。

由此，本文对沪深市场联动风险进行测算。首先，利用GARCH(1,1)-t模型分别描述沪深市场的波动特征，进而利用t-Copula函数捕捉沪深市场联动风险特征，同时得出沪深市场风险因子联合分布函数，最后利用拟蒙特卡罗方法模拟沪深市场联动风险并且对其进行测算。

图1 蒙特卡罗随机数

图2 拟蒙特卡罗随机数

二、金融市场联动风险测算理论基础

(一)市场联动风险模型

1.风险因子波动模型

选择合适的边缘分布模型以刻画金融时间序列的波动特征是利用Copula函数进行金融市场联动风险建模的重要一步。鉴于上证指数和深证指数编制方法具有科学性，可以充分反映沪深金融市场的波动特征。本文利用边缘分布模型拟合上证指数和深证指数金融时间序列，将沪深金融市场的波动特征充分反映在边缘分布模型中。随着我国金融市场的不断发展，金融衍生品层出不穷，证券市场交易量空前增长，特别是在当前一系列“黑天鹅”事件的影响下，股指收益率序列多呈现高峰、厚尾、波动聚类和长记忆性等特征。t-GARCH模型可以较好地刻画这些波动特征，特别是厚尾特征。针对金融时间序列的波动特征，本文建立t-GARCH模型刻画股指收益率序列的波动特征，t-GARCH模型的表现形式如下：

Rnt=μn+εnt,t=1,2,…,T

(1)

(2)

(3)

2.市场联动风险特征的描述

根据Copula建模思想，Copula函数反映多变量时间序列的相关结构特征，在建立金融市场联动风险测算模型过程中，这种由Copula函数描述的市场相关结构表现为市场联动特征。由于受到金融全球化趋势、国际巨额游资以及国内金融改革措施不断推进的影响，特别是一系列“黑天鹅”事件的影响，我国沪深金融市场联动特征呈现高峰厚尾、时变波动特征。二元t-Copula函数具有较厚的尾部，对尾部变化较为敏感，可以迅速捕捉金融市场联动风险的尾部变化特征。也就是说，二元t-Copula函数能够较为准确地预测到当一个金融市场出现上涨(下跌)时，另一个金融市场同时出现上涨(下跌)的可能性。由此，本研究结合t-Copula函数在捕捉金融市场尾部变化时的优势，利用t-Copula函数对沪深金融市场联动特征进行充分描述。

二元t-Copula函数分布函数和密度函数的表现形式如下：

(4)

(5)

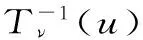
3.市场联动风险模型拟合检验

学者大多选择AIC指标和平方欧氏距离来判断Copula函数拟合相关模式的优劣程度。AIC的计算方法可表示为:

AIC=-2L+2n

(6)

其中,L表示极大似然函数值，n表示待估参数个数，AIC值越小表示模型拟合程度越好。

平方欧氏距离的计算公式可表示为：

(7)

其中，ui和vi分别表示上证指数和深证成指的经验分布函数，C′(ui,vi)为经验Copula函数，C(ui,vi)为Copula函数的估计值。d2值越小，Copula函数的拟合效果越好。

(二)市场联动风险测算原理

论文利用拟蒙特卡罗模拟方法生成随机数，模拟沪深股指序列的未来收益率。然而这些随机数是一种理想化的序列，因此，需要对随机数序列进行转化，以服从t-Copula-GARCH市场联动风险模型假设。从理论上分析，利用随机数模拟的步骤如下：

第一步，生成两个相互独立的随机数u和w。

第三步，重复上述步骤k次，可得到服从模型假设的两个随机数序列uk×1和vk×1，其中(u,v)～C(u,v)。可以根据模拟次数的需要变动k值。以模拟1 000次为例,利用拟蒙特卡罗模拟方法生成的随机数经过转换后的散点图如图3所示。图3表示利用拟蒙特卡罗模拟方法生成的随机数转换后的撒点图比较均匀。

图3 拟蒙特卡罗随机数转换

三、沪深市场联动风险测算实证过程及结果分析

(一)数据描述性分析

本文选取上证指数(简称SH)和深证成指(简称SZ)为研究对象，选择时间段为2010年1月4日至2016年8月22日，共1 612个数据。定义收益率Rt=ln(Pt)-ln(Pt-1)。对两个收益率序列进行描述性统计，结果如表1。表1括号内为相应统计量的概率值。

从上证指数和深证成指收益率的描述性统计可以看出，这两个指数收益率序列均成右偏特征，它们的峰度值都大于3，说明上证指数和深证成指收益率序列都不服从正态分布。从ADF值可以看出，上证指数和深证成指收益率序列不存在单位根。

从图4和图5可以看出，上证指数和深证成指收益率序列具有明显的ARCH效应，即一个大的波动后面会有很多大的波动，一个小的波动后面会有很多小的波动。结合表1的描述性统计特征，上证指数和深证成指收益率序列具有左偏、高峰、后尾特征。

(二)沪深市场波动特征

GARCH(1,1)模型可以刻画金融时间序列的高峰、厚尾、波动聚类和偏斜等异常波动情况，模型残差服从t分布的假设更符合当前沪深股市的波动情况。因此，本文建立GARCH(1,1)-t模型描述上证指数和深证成指收益率序列的边缘分布波动特征。GARCH(1,1)-t模型参数估计结果如表2所示。

根据t检验的结果，GARCH(1,1)-t模型对上证指数和深证成指的股指收益率序列拟合较好。由表2得出两个指数收益率序列的自由度是不相等的，上证指数的自由度小于深证成指的自由度，这表明上证指数收益率序列的分布特征具有更厚的尾部，出现极端事件的概率较大。

表1 SH和SZ的描述性统计结果

图4 上证指数收益率序列波动图像

注：括号内为相应参数估计值的t统计量，***、**、*分别表示在99%、95%、90%置信水平上显著。

(三)沪深市场联动风险特征分析

表2中的K-S统计量及其概率值是根据对原序列残差进行概率积分变换然后进行K-S检验，检验序列是否服从(0,1)均匀分布得到的。对GARCH(1，1)-t模型做残差自相关检验，残差自相关如图6和图7。图6和图7表明两股指收益率序列的残差不存在自相关。K-S统计量及其概率值表明两个序列服从(0,1)均匀分布，并且不存在自相关，可以建立t-Copula函数模型。t-Copula函数的参数估计结果如表3所示。

图6 SH残差自相关

图7 SZ残差自相关

参数平方欧式距离(d2)AICt-Copulaρ0.93430.0153-11.5640ν4.1308

t-Copula函数对市场联合风险的尾部变化比较敏感，可以较好捕捉金融资产相关结构的尾部特征。t-Copula函数在拟合上证指数和深证成指收益率序列的相关结构时表现出来的优势表明沪深两市股指收益率的波动特征呈现厚尾特征，并且基于Copula理论的相关性指标ρ的估计值接近于1，说明沪深股市的正相关性较强，协同运动特征明显。这种波动特征反映在现实经济交易中表现为，当上证指数出现上涨或下跌时深证成指出现上涨或下跌的概率较大，特别是在极端事件爆发时，沪深两市之间波动传导迅速。

(四)模拟结果分析

在得出基于沪深两市指数收益率的联合分布模型及其特征后，基于t-Copula-GARCH(1,1)模型，本文利用拟蒙特卡罗方法模拟沪深指数收益率序列的未来收益率变动情况，测算沪深市场联动风险。本文首先根据“失败频率检验法”求出模拟次数在300次、500次、700次、900次、1 000 次的情况下，分别在不同置信水平上的失败次数可接受区间，并且统计出利用拟蒙特卡罗方法在不同模拟次数和置信水平下的模拟在险价值失败次数，结果如表4和表5所示。

表4 不同置信水平上的失败次数可接受区间

表5 拟蒙特卡罗方法模拟在险价值的失败次数

对比表4和表5可以看出，利用拟蒙特卡罗方法测算结果的失败次数都落在了可接受区间内，这表明拟蒙特卡罗方法通过了回测检验，模拟精确度较高。从图8—图11可以看出，在90%、95%、99%和99.5%置信水平上，利用拟蒙特卡罗模拟方法分别在模拟次数900次、3 000次、5 000次和1 000次时，沪深市场联动风险测算结果已经开始收敛，收敛速率较快。

图8 90%置信水平上结果统计

图9 95%置信水平上结果统计

图10 99%置信水平上测算统计

图11 99.5%置信水平上结果统计

四、结语

随着金融全球化发展，金融市场波动特征发生巨大变化，特别是当前伴随着一系列“黑天鹅”事件的发生，对机构投资者测算金融市场联动风险的精确性和高效性提出了更高的要求。为测算沪深金融市场联动风险，本文建立t-Copula-GARCH(1,1)模型描述沪深金融市场波动特征和相关结构特征，进而利用拟蒙特卡罗模拟方法测算沪深金融市场联动风险。测算结果表明：拟蒙特卡罗模拟方法的收敛速率快，模拟结果都通过了回测检验，精确度高，这为机构投资者测算金融市场联动风险提供了一种科学的参考方法。

[1] SKLAR A.Fonctions De Repartition a n Dimensions et Leurs Marges[J].Publication De l’Institut De Statistique de l’Universite De Pairs,1959,8:229-231.

[2] BOUYE E,DURRLEMAN V,NIKEGHBALI A et al.Copulas for finance:A reading guide and some applications[Z].Financial Econometrics Research Centre,City University Business School,London,2000.

[3] ENGLE R F.Autoregressive heteroskedasticity with estimation of the variance of U.K.inflation[J].Econometrica,1982,50:987-1008.

[4] BOLLERSLEV T.Generalized autoregressive conditional heteroskedasticity[J].Journal of Economics,1986,31:307-327.

[5] 张尧庭.连接函数技术与金融风险分析[J].统计研究，2002(4)：48-51.

[6] 张明恒.多金融资产风险价值的Copula计量方法研究[J].数量经济技术经济研究，2004(4):67-70.

[7] 韦艳华，张世英.金融市场的相关性分析——Copula-GARCH模型及其应用[J].系统工程，2004，22(4)：7-12.

[8] 张自然，丁日佳.人民币外汇市场间不对称汇率变动的实证研究[J].国际金融研究，2012(2)：85-95.

[9] 谢赤，张鹏，曾志坚.开放进程中人民币汇率间相依性研究——基于动态Copula-GJR-t模型的分析[J].金融经济学研究，2014(1)：79-90.

[10]高波，任若恩.基于时变Copula模型的系统流动性风险研究[J].国际金融研究，2015(12)：85-93.

[11]欧阳资生，刘远，罗长青.基于Copula方法的信用利差与市场风险相关性度量[J].统计与决策，2016(1)：151-155.

[12]向为民,张箭.蒙特卡洛模拟法在项目评估风险分析中的应用——以青岛海信房地产目标成本测算工具表为例[J].重庆理工大学学报(社会科学),2015(7):48-52.

(责任编辑 魏艳君)

Application Research of t-Copula-GARCH Model on the Calculation of Shanghai and Shenzhen Markets Linkage Risk: Based on Quasi Monte Carlo Simulation Method

LIU Xin, WANG Fuhao

(School of Economics and Finance, Chongqing University of Technology, Chongqing 400054, China)

In order to calculate the financial market linkage risk of Shanghai and Shenzhen, this paper selects the return rate of Shanghai Composite Index and SZSE Component Index as research object. Firstly, according to Copula model construction theory, this paper uses the GARCH-t model and t-Copula function respectively to fit the volatility of Shanghai and Shenzhen stock index portfolio return rate and the characteristics of Shanghai and Shenzhen financial market linkage risk. Further, it applies Quasi Monte Carlo simulation method to simulate the future return rate series of Shanghai Composite Index and SZSE Component Index, and calculates the financial market linkage risk of Shanghai and Shenzhen. Empirical results show that the convergence rate of the Quasi Monte Carlo simulation method is fast, and the stability and accuracy of the result simulated by Quasi Monte Carlo are more stable and precise. The advantages of Quasi Monte method can help institutional investors to manage financial market risk effectively, which has a profound significance for institutional investors to make scientific investment decisions.

institutional investor; financial market linkage risk; copula model construction; Quasi Monte Carlo simulation method

2016-10-15

重庆理工大学研究生创新基金重点项目“基于拟蒙特卡罗方法的Copula-GARCH模型在金融风险计量中的应用研究”(YCX2015106)

刘新(1970—)，女，重庆人，教授，博士，研究方向：微观金融、财政学。

刘新，王福豪.t-Copula-GARCH模型在沪深市场联动风险测算中的应用研究——基于拟蒙特卡罗模拟方法[J].重庆理工大学学报(社会科学)，2017(6):36-43.

format：LIU Xin,WANG Fuhao.Application Research of t-Copula-GARCH Model on the Calculation of Shanghai and Shenzhen Markets Linkage Risk:Based on Quasi Monte Carlo Simulation Method[J].Journal of Chongqing University of Technology(Social Science)，2017(6):36-43.

10.3969/j.issn.1674-8425(s).2017.06.006

F830.9

A

1674-8425(2017)06-0036-08