基于磁压等效双二维模型的绕组损耗仿真
2017-07-07,
,
(福州大学电气工程与自动化学院,福建 福州 350108)
1 引言
从高频磁技术开始发展以来,绕组损耗的研究就一直没有中断过。它的研究主要分为两大部分,一是理论分析和仿真分析的研究;一是实物测量的研究。绕组损耗的理论计算模型都是依据Maxwell方程组进行推导和简化的,其中比较常用的有Dowell模型和Bessel函数,但各有其缺陷。文献[1-2]介绍了一些改进的计算模型,然而这些算法都难以避免地使用了简化的方式,其局限性和精度低的缺点乃至于最后需要修正系数或修正函数的宿命都是无法摆脱的。而对于磁损耗的实测方法有很多,最常用的有交流功率计法、直流法和量热法,但这些方法都无法有效地将磁损耗中的绕组损耗和磁芯损耗分开[3-4]。
仿真分析脱胎于有限元素法,它通过泛函变分的方式直接将场控制方程转化为泛函极值问题,并利用数值分析法求它的数值解[5]。由于它直接求解场控制方程,而没有经过简化,所以从理论上来说,只要仿真模型合适,它的解是最精确的。虽然实测方法更加可靠和一目了然,但由于其操作困难,容易造成偏差,而且工程量大,又耗时耗力,所以基本上只作为一种验证和评估的手段;而产品在设计和优化阶段用的更多的是理论分析和仿真,再从其精确度来取舍,显然,仿真分析是研究者和设计者的首选。
本文首先从仿真分析的现状出发总结三维模型仿真和单二维模型仿真的缺陷;从而提出双二维模型并分析其优势和存在的一些问题;然后通过对双二维模型所存在问题的分析,总结双二维模型磁压等效的必要性,提出并详细分析添加补偿电流的磁压等效方式。最后通过有限元仿真软件Ansoft对三维模型、单二维模型和双二维模型进行绕组损耗仿真,并用三维模型仿真结果作为基准,以证明双二维模型的准确性和有效性。
2 仿真分析的现状和双二维模型的提出
仿真分析虽然解决了Dowell模型和Bessel函数模型等绕组损耗计算模型的局限性和精度问题,但同时其庞大的仿真时间消耗和内存资源占用也成为了主要矛盾,尤其是对于稍微复杂的磁元件三维模型仿真,计算机内存资源往往是不够的,而且仿真时间也太长,极其不便于设计和研究。所以在工程应用和学术研究中人们通常是将三维磁元件近似为一个单二维模型,然后再进行仿真。然而这种做法存在很大误差,其根本原因是单二维模型无法完整地体现出三维模型的磁场分布特性[5-6]。如图1所示,以常见的EE型磁芯为例,将一个实际三维磁件近似为一个单二维模型,显然它只能勉强描述出X-Y平面的磁场分布情况,对于Y-Z平面的磁场分布则无法描述,而且由于两个平面磁场分布的差异性,单二维模型将会带来很大误差。
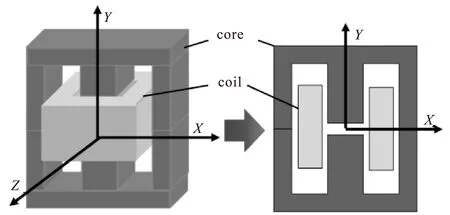
图1 单二维模型的创建图
为了能够更加完整地描述三维磁场分布,本文在原单二维模型的基础上,再添加一个二维模型用来描述Y-Z平面的磁场分布,也就是双二维模型[7-8]。如图2所示,仍以EE型磁芯为例,双二维模型的处理方式就是将实际三维磁件分解为X-Y平面和Y-Z平面两个二维模型,然后将各自的绕组损耗仿真结果与各自面域内的绕组长度相乘,最后再将两者相加,即可得到最终的绕组损耗。
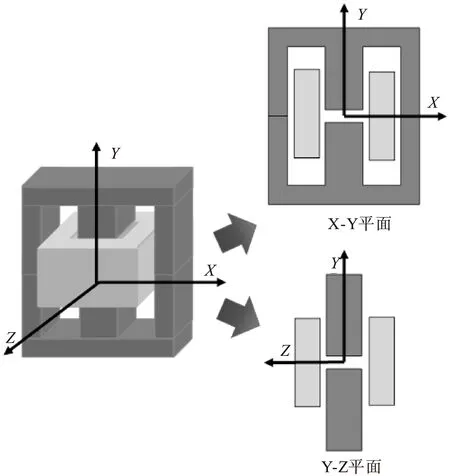
图2 双二维模型的创建图
3 双二维模型磁压等效的必要性和方法
前文介绍的双二维模型的创建仅仅是将实际三维磁件上X-Y面和Y-Z面的正视图所包含的磁芯和绕组绘制出来。这种做法本身就是对于三维模型的一种简化,会带来一定的不完整性。尤其是对于Y-Z面的模型来说,因为只有在磁芯中柱包围绕组,所以只要绘制中柱的Y-Z面模型即可,但是这种处理方式会导致Y-Z面模型无法像X-Y面模型一样将边柱磁芯绘制出来。这种现象对于无气隙的磁件来说结果影响不大,因为绕组周围的磁通分布并没有随着这种现象而发生很大变化。但它对于带气隙的磁件来说将会造成很大影响,如图3所示,边柱磁芯的缺失导致磁芯无法构建回路,主磁通必须经过空气才能从中柱的上半部分回到下半部分,这与实际三维磁件的主磁通所走路径不符,导致磁压大部分都降落在空气磁阻上,只有很少的一部分由气隙磁阻承担,而实际三维磁件的磁压应绝大部分由气隙承受。也就是说,二维模型的气隙磁压将远小于实际三维磁件的气隙磁压。气隙磁压不同导致气隙附近的磁场分布不同。而对于带气隙磁件来说,气隙边缘效应又是绕组涡流损耗最主要的产生因素,所以最终使得绕组损耗发生很大改变。所以,创建出正确的双二维模型的先决条件是需要先将二维气隙磁压等效为实际磁件的气隙磁压。下面将详细讨论磁压等效的方法。
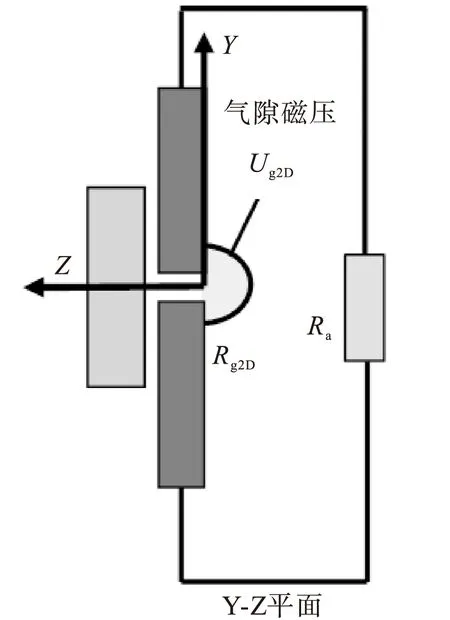
图3 带气隙电感Y-Z面磁路模型
对于带气隙磁件,由于磁芯磁导率远大于空气磁导率,所以绕组产生的安匝磁动势几乎都由气隙磁压承受。相应的,对于无气隙的变压器,原边激磁绕组产生的安匝磁动势则都由副边感应绕组的感应电流产生的反磁势来承受。所以,可以说气隙产生的效果与感应绕组相同,也就是说,气隙磁压可以用绕组的安匝磁动势代替。因此,当二维模型的气隙磁压与实际磁件气隙磁压不等时,可以在气隙处添加一个类似于气隙等效绕组的补偿电流或者直接用它代替气隙,用以补偿气隙磁压,使得二维模型的气隙磁压等于实际磁件的气隙磁压,如图4所示。
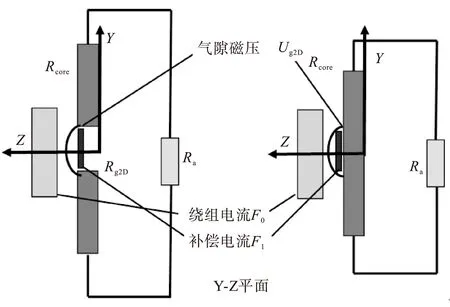
图4 磁压等效模型原理图
由于补偿电流加在气隙处,而且其效果等同于气隙,所以对于激磁绕组而言,尽管添加了补偿电流,但并不改变气隙附近的磁场分布形状,再将气隙磁压进行磁压等效以改变气隙磁场的大小,则可令二维模型的气隙磁场分布形状和大小都与实际磁件相同。
为了求得补偿电流的大小,首先需要确定磁压等效的目标磁压大小,也就是说需要得到实际磁件的气隙磁压。因为磁芯的磁导率远大于空气磁导率,因此即使磁芯磁导率会随着频率变化,磁件的磁压分配也不会随着频率变化而发生很大改变;另外,绕组的涡流分布同样不会影响磁压的分配。所以在获取三维磁件的气隙磁压时,可以直接采用三维静磁场仿真,其中绕组可以采用简化绘制,只要形状和安匝大小保持不变即可,这样就可以避免三维涡流场仿真需要剖分细致导致内存不足和仿真时间过长的问题。图5给出了磁件三维模型和其简化绕组模型,表1为磁件三维模型静磁场仿真、100 kHz涡流场仿真和简化绕组三维模型静磁场仿真的气隙磁压仿真结果,显然气隙磁压大小几乎不受频率大小和涡流分布的影响。
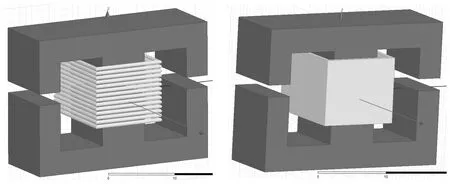
图5 磁件三维模型和其简化绕组模型
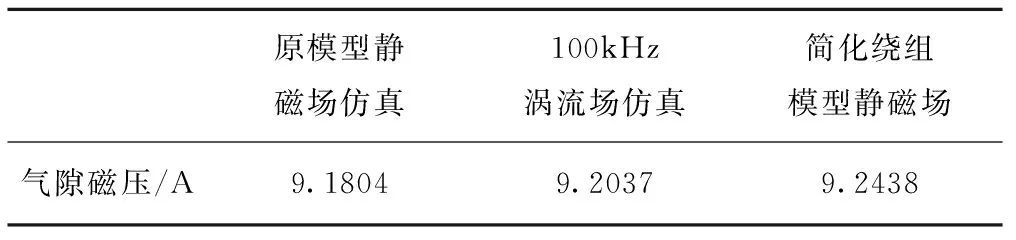
原模型静磁场仿真100kHz涡流场仿真简化绕组模型静磁场气隙磁压/A9.18049.20379.2438
目标磁压获得之后,为了推算出补偿电流的大小,需要对二维模型进行磁路分析。以Y-Z面模型为例,磁路模型如图4所示,可得其磁路方程:
(1)
其中,F0和F分别表示激磁绕组和补偿电流产生的安匝磁动势,Ug2D表示二维气隙磁压,各磁阻表示含义如图4所示,Rg2D0和Rg2D分别表示激磁绕组和补偿电流对应的气隙磁阻。由于磁阻不随补偿电流大小变化,所以可将式(1)简化为式(2):
Ug2D=F0·A0+F·A1
(2)
为了求得磁阻系数A0和A1的大小,可以设置两个不同的补偿电流F1和F2,再进行仿真求得相对应的气隙磁压Ug2D1和Ug2D2,然后分别代入到式(2)即可求出磁阻系数的大小,再将三维气隙目标磁压Ug3D和所求出的磁阻系数以及激磁电流安匝磁动势F0代入到式(2),即可得补偿电流安匝磁动势F的表达式:
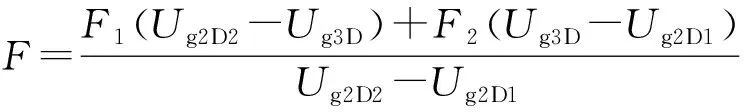
(3)
其中,所有仿真所求得的气隙磁压都可由Ansoft软件仿真得到的磁场强度H线积分求得,具体操作为在气隙两端绘制圆弧线,使之跨过整个气隙并且将补偿电流包在中间,再使用仿真软件的场计算器通过式(4)计算即可,圆弧线绘制如图4所示,场计算器计算气隙磁压图如图6所示。
(4)
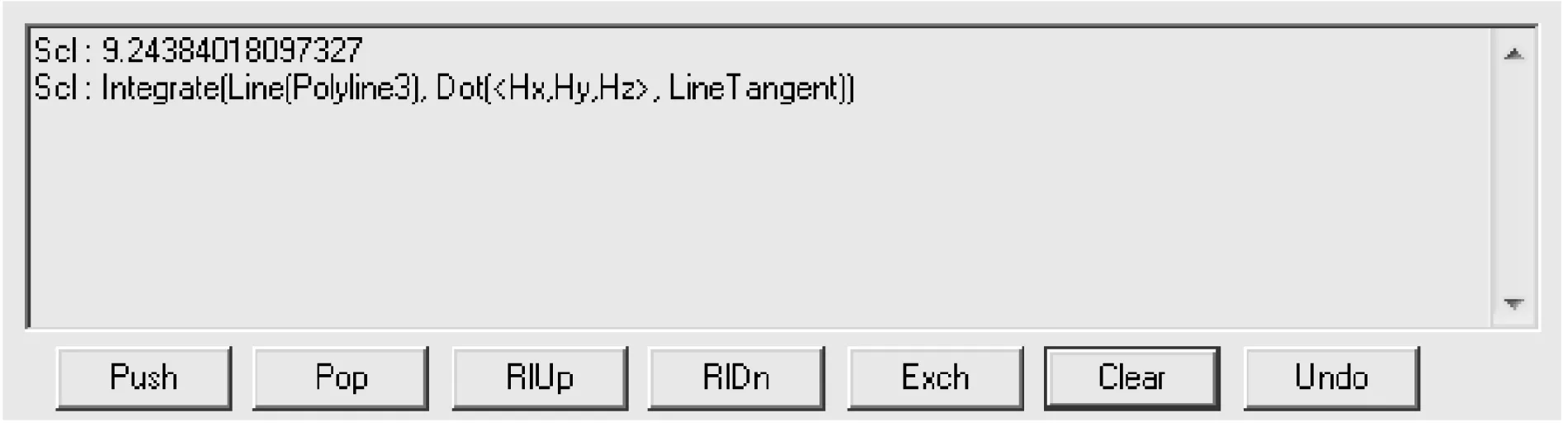
图6 场计算器计算气隙磁压图
将补偿电流大小求出之后,即可进行相应二维模型的损耗仿真,再按第二节所示的处理方式即可由式(5)求得总的绕组损耗。式(5)中,PX-Y和PY-Z分别为磁压等效之后的X-Y面和Y-Z面二维模型最终的单位深度绕组损耗仿真结果,LX-Y和LY-Z分别为各自面域内绕组长度,因为用于仿真的二维模型为一半的模型,所以绕组长度还要再乘以2。这种磁压等效法无论对于诸如EE型磁芯的方形绕组抑或是如EC型磁芯的圆形绕组都是可行的,没有绕组形状的限制;而且因为一个补偿电流对应一个气隙,所以该磁压等效法也同样适用于多气隙的磁件。
P=PX-Y·2LX-Y+PY-Z·2LY-Z
(5)
4 仿真验证
为了验证磁压等效双二维模型的正确性,本文以三维模型绕组损耗仿真为基准,分别对单二维模型(即X-Y面二维模型)、未磁压等效的双二维模型和磁压等效的双二维模型进行绕组损耗仿真。其中磁压等效的目标气隙磁压直接取自三维简化绕组模型的静磁场仿真。图7给出了三维模型、单二维模型和双二维模型图,图8给出了各模型的交流电阻仿真结果随频率变化的曲线图和以三维模型交流电阻值为基准,各二维模型交流电阻的相对误差随频率变化的曲线图。
由图易知,单二维模型的误差最大,其次是未磁压等效的双二维模型,最小的是磁压等效双二维模型,其误差精度在10%以内,足以满足工程需求。
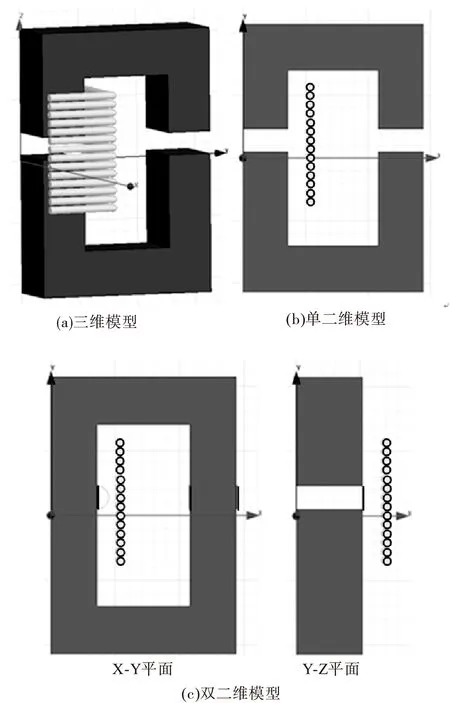
图7 三维模型、单二维模型和双二维模型图

图8 各模型交流电阻仿真结果和相对误差图
5 结语
本文通过绕组损耗的有限元仿真,对磁压等效双二维模型进行了细致的分析与研究,并完成了其精度的验证,得出以下结论:
(1)绕组损耗的研究主要有理论分析、仿真分析和实测评估等方法,而因为实测操作困难,容易造成偏差又耗时耗力,理论分析局限性大且精度低,所以在产品设计优化时,多用仿真分析。
(2)根据绕组损耗仿真的发展现状,三维仿真对于内存要求过高,耗时过长。作为替代的单二维模型因无法完整描述三维磁场分布而精度过低。而双二维模型可以解决这些问题,最适用于绕组损耗仿真。
(3)磁压等效是双二维模型能够正确创建的先决条件,只有先将二维气隙磁压等效为实际磁件气隙磁压了,双二维模型才有其意义和准确性,可以采用气隙处添加补偿电流或直接用该补偿电流安匝磁动势代替气隙磁压的方式进行磁压等效。
(4)以三维模型绕组损耗仿真作为基准,验证了磁压等效双二维模型的准确性,其精度在10%以内,足以满足工程需求。
[1] Xi Nan,Charles R Sullivan.An Improved Calculation of Proximity-Effect Loss in High-Frequency Windings of Round Conductors.IEEE PESC′03,2003,34(2):853-860
[2] W.Chen,X.Huang and J.Zheng,“Improved winding loss theoratical calculation of magnetic component with air-gap,” Power Electronics and Motion Control Conference(IPEMC),2012 7th International,Harbin,China,2012,pp.471-475.
[3] 汪晶慧,陈为.超低损耗角磁心高频损耗测量方法[J].电工技术学报,2012,27(11):133-138.
[4] 龚宇,崔巍,章跃进.考虑局部磁滞损耗的复合电机铁损耗计算[J].中国电机工程学报,2014,34(30):5395.5400.
[5] M.M.Koo,J.Y.Choi,K.Hong and K.Lee,“Comparative Analysis of Eddy-Current Loss in Permanent Magnet Synchronous Machine Considering PM Shape and Skew Effect Using 3-D FEA,” in IEEE Transactions on Magnetics,vol.51,no.11,pp.1-4,Nov.2015.
[6] M.Taghizadeh Kakhki,J.Cros and P.Viarouge,“New Approach for Accurate Prediction of Eddy Current Losses in Laminated Material in the Presence of Skin Effect With 2-D FEA,” in IEEE Transactions on Magnetics,vol.52,no.3,pp.1-4,March 2016.
[7] R.Prieto,J.A.Cobos,O.Garcia,P.Alou and J.Uceda,“Model of integrated magnetics by means of ”double 2D“ finite element analysis techniques,” Power Electronics Specialists Conference,1999.PESC 99.30th Annual IEEE,Charleston,SC,1999,pp.598-603 vol.1.
[8] R.Prieto,J.A.Cobos,O.Garcia,P.Alou and J.Uceda,“Study of 3-D magnetic components by means of ”double 2-D“ methodology,” in IEEE Transactions on Industrial Electronics,vol.50,no.1,pp.183-192,Feb 2003.
