加强物理模型教学提升学生抽象思维能力

徐 斌

(常州市第一中学,江苏 常州 213003)

大中物理衔接

加强物理模型教学提升学生抽象思维能力

徐 斌

(常州市第一中学,江苏 常州 213003)

物理模型是人们为了从事研究而建立的对原型高度抽象化、理想化的思维客体，是抽象思维的产物。抽象思维的深刻性和灵活性反映了学生思维品质的优劣，通过加强物理模型教学，消除思维障碍，克服思维定势，加强思维训练，对提升抽象思维能力是有益的。

物理模型;抽象思维

1 一根细绳引发的争论

两位学生为解一道习题，得出不同的答案，各执其词，是非难分，发生了激烈的争论。这道题是：如图1所示，质量为m的物体系于长度分别为l1、l2的两根细绳上，l1的一端悬挂在天花板上，与竖直方向夹角为θ，l2水平拉直，物体处于平衡状态。现将l2绳剪断，求剪断瞬时物体的加速度(由上海高考题改编)。

学生甲的解法如下：设l1绳上拉力为T1，l2绳上拉力为T2，重力为mg，物体在3个力作用下保持平衡T1cosθ=mg，T1sinθ=T2，T2=mgtanθ，剪断绳的瞬间，T2突然消失，物体即在T2反方向获得加速度。因为mgtanθ=ma，所以加速度a=gtanθ，方向在T2反方向，如图2所示。

学生乙的解法是：当细绳l2剪断后，物体受到重力和细绳l1的拉力，如图3所示，小球将在与细绳l1垂直的方向获得加速度a=gsinθ。

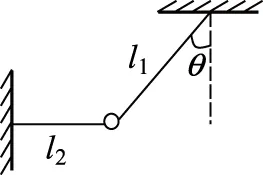
图 1

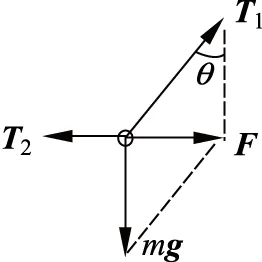
图 2

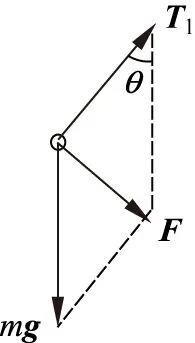
图 3

分析一下两位学生的解法之所以不同，是因为他们进行受力分析的时候，对细绳所建立的物理模型不同造成的。虽然他们都忽略了细绳的质量，但学生甲把细绳当作弹性体模型，即有弹力，且形变不能忽略，产生形变或恢复形变都需要一定的时间。当细绳l2被剪断的瞬时，细绳l1的形变没有改变，它的弹力T1仍与细绳l2剪断前相同，即与小球处于3个力平衡时相同，所以T1=mg/cosθ。小球所受合力F=mgtanθ，加速度a=gtanθ。学生乙却把细绳当作刚性体模型，即有弹力，而形变极小，可以忽略不计。因此产生形变或恢复形变的时间极短，也可以忽略不计。当细绳l2剪断后，细绳l1对小球所受的弹力与l2剪断前不同，变为T1=mgcosθ，小球所受的合力F=mgsinθ，所以a=gsinθ。

实际上，细绳既不能理想化为像轻质弹簧一样绝对的弹性体，也不能理想化为像轻杆一样的纯粹的刚性体，而是介于两者之间。因此，小球的加速度大小也是介于gtanθ与gsinθ之间。

从学生的争论可以看出，建立正确逼真的物理模型对解决问题起着不可替代的重要作用。物理学理论其实就是由一个个模型理论组成的，模型思想和模型方法贯穿了整个物理学。毫不夸张地讲，学习和利用物理的过程就是通过建立和使用物理模型来描述、解释、揭示物理现象及其规律的过程。

2 物理模型及其特征

2.1 什么叫物理模型？

物理学研究的对象是自然界中最普遍的物质运动现象。物质运动的表现形式和特征是千变万化、千姿百态的。物质运动过程往往受到自身和周围环境中各种因素的影响、制约。我们研究实际问题时，如果不加分析地把所有因素全部考虑进去，那么势必增加研究问题的难度，甚至无法研究。因此为了描述物质及其运动规律，我们必须抓住主要因素，舍弃次要因素；把握必然联系，排除偶然联系；透过表面现象，揭示内在本质，从而把复杂的物理问题简单化，具体的物理问题理想化，建立起能体现客观事物本质特征的抽象的物理模型。用物理模型代替实际的研究对象，然后加以研究，这是物理学的基本方法，叫做模型方法。由此可见，物理模型是人们为了从事研究而建立的对原型高度抽象化、理想化的思维客体。

常见物理模型可分为3类：客体模型、条件模型和过程模型[1]。物理学所研究的客观存在的实际物体，通过简化、抽象建立起来的物理模型叫客体模型，例如，质点、刚体、点电荷、点光源、理想气体、理想变压器等；客体在运动、变化过程中，总要受到各种条件制约，使问题变得繁杂，为了便于研究，对制约客体运动、变化的条件进行取舍，忽略次要因素，抓住决定性条件，突出理想客体与主要条件的内在联系，这样建立起来的理想化的条件叫条件模型，例如，光滑平面、轻绳、轻弹簧、轻杆、绝热容器、不计电阻的导线、均匀介质等；理想客体在理想条件下的运动、变化过程是一个高度抽象的物理过程，称为过程模型，例如，自由落体运动、匀速直线运动、简谐运动、弹性碰撞、等温变化、绝热过程等。

2.2 物理模型的两个主要特征

(1) 抽象性与形象性的统一

一般情况下，物理模型的建立过程是一个抽象思维和形象思维相结合的过程，而建立的模型本身又是抽象性和形象性的统一体。例如，质点模型的建立主要利用了抽象的方法，用一个没有大小、形状，只具有与实际物体(具有形象性)等质量的几何点(具有抽象性)来代替，质点就是抽象性与形象性的统一体。

(2) 科学性和近似性的统一

物理模型不仅反映了原型的直观形象和主要特征，而且是以科学知识和实验事实为依据抽象概括建立起来的，具有一定的科学性。另一方面，任何模型只是对客体的近似描述而已，其正确性要靠实验来检验。历史上，人们对原子结构模型的建立，从汤姆生的“葡萄干布丁”模型，到卢瑟福的原子有核模型，再到原子结构的玻尔模型，直到量子力学中电子云模型，都说明了建模要依据实验事实，也要接受新的实验事实的检验。

3 加强物理模型教学，提升学生抽象思维的能力

物理模型的建立，模型方法的运用，是与抽象思维活动密不可分的。抽象思维最基本的特点是抽象性和概括性。抽象就是要忽略次要，突出主要，提炼出本质因素。概括就是在抽象的基础上，把抽象过程获得的物理模型的本质属性，推广到同类客体及其过程中去，掌握它们共同的一般的属性。抽象思维的抽象程度越高，概括的广度越大，物理模型离开客观事物就越远，但离真理也就越近。在物理模型教学中，我们可以根据抽象思维的特点，渗透模型方法，不断提高学生的抽象思维能力。

3.1 消除心理障碍，认清物理模型的科学性

学生受传统教学的影响，往往追求精确、讲究绝对，对忽略某些次要因素总是不放心，认为科学是不能容忍近似的，科学就应该百分之百精确。这是片面的、脱离实际的心理观念，是掌握模型方法、提升抽象思维能力的障碍。

教学中可以通过具体的实例，说明近似是允许的，不会产生很大的偏差，却能使问题简化，可以得到满意的解决。

案例分析1

汽车长L=8m，以速度8m/s做匀速运动，通过一座长为s1=40m的桥时，需要多少时间？若通过一条长为s2=2000m的隧道时，需要多少时间？

分析与解： 当汽车过桥时，汽车的长度L与桥长s1相比较是不能忽略的，所以汽车过桥的时间为

而汽车过隧道时，车长L与隧道长s2相比较，就可以忽略了，汽车可以作为质点，求得汽车过隧道的时间为

如果考虑汽车的长度，求得时间是251s，所以相对误差是0.4%，这是允许的。如果汽车通过的路程更长，误差就更小，用质点这个模型代替汽车就更有必要了。

案例分析2

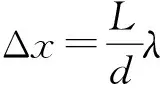
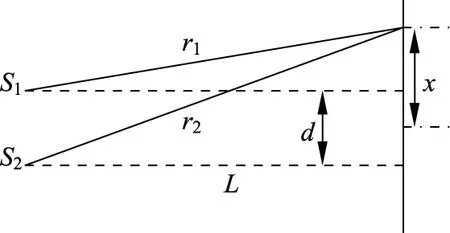
图 4

只要了解学生学习物理的心理，善于抓住具体问题进行分析，弄清哪个是决定事物变化的主要因素，哪个是无关轻重的次要因素，哪个是干扰主流的偶然因素，就能使学生理解建立物理模型的必要性和科学性，提高抽象思维的自觉性，促进抽象思维的发展。

3.2 类比中克服思维定势，提高抽象思维的灵活性

明确了建立物理模型的必要性，掌握了质点等基本的物理模型，一些学生往往会形成一种思维定势，把一个客观的物理问题，不加分析地类比到某个熟悉的物理模型，从而误入歧途，使问题难以解决。例如，试证明：浮在水面的长方形木块，用手往下按一下木块后，木块就做简谐运动。由于教科书中研究单摆和弹簧振子的简谐运动时，都把振动物体当作“质点”来处理，所以学生就形成思维定势，不加分析地把水面上振动的木块也当作质点，把思维引入误区，问题无法解决。教学中可引导学生分析木块的受力情况，绝大多数学生都知道水的粘滞阻力可以忽略，木块除受重力作用外，还受到水的浮力作用。因此，木块的体积是不能忽略的，浮力的大小直接跟木块浸入水中的体积有关，木块不能当作质点处理。建立了正确的物理模型，问题就可迎刃而解了。

由此可见，物理模型不是完全由研究对象所决定，还与研究对象所处的环境，即它的运动、变化情况有密切关系。在建模中运用类比方法是值得提倡的，它可以起到举一反三、触类旁通的作用，但要将两类具有许多相同因素的客体加以比较，抓住相同因素的本质。

案例分析3

老鼠离开洞穴沿直线前进，它的速度与到洞穴的距离成反比，当它行进到离洞穴为d1的甲处时的速度为v1，则它行进到离洞穴为d2的乙处时用去的时间为多少？

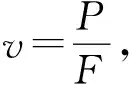
当x=d1时，v=v1，代入上式可得

再根据外力做的功等于弹簧弹性势能的增量，得

最终可得

将汽车恒功率运动模型和弹簧模型运用到老鼠的运动中来，独具匠心，一个难题因此而显得清晰且简单。进行抽象思维，建立物理模型，没有固定不变的模式，应该针对具体问题进行具体分析，紧紧抓住决定物体运动特征的本质属性，排除次要因素的干扰，可以提高思维的灵活性[2]。

3.3 加强思维训练，提高抽象思维的深刻性

抽象思维的深刻性是一切思维品质的基础。在物理模型教学中，加强思维训练，对于学生抽象思维的深刻性是十分有益的。

1) 深入理解物理概念和规律，掌握物理公式的成立条件

物理公式是基于物理模型，运用物理概念来揭示物理规律，它是反映了相关物理量之间关系的数学表达式，都是有条件的。如牛顿运动定律只适用于宏观物体在惯性系中的低速运动问题，库仑定律只适用于真空中静止的点电荷等，在理解物理公式和应用它们解决实际问题时，一定要注意公式的成立条件，否则就会导致错误的结论。教学中可以留心学生学习中常见的错误，作为教学的资源，在帮助学生纠正错误物理模型的的过程中，暴露学生抽象思维中的不足、方法上的欠缺，使学生对物理模型得到更为深刻的认识，抽象思维能力也得以深化。

案例分析4

某行星绕太阳运行的椭圆轨道如图5所示，F1和F2是椭圆轨道的两个焦点，太阳在焦点F1上，A、B两点是两个焦点连线与椭圆轨道的交点，已知A点到F1的距离为a，B点到F1的距离为b，则行星在A、B两点处的速率之比为多大？

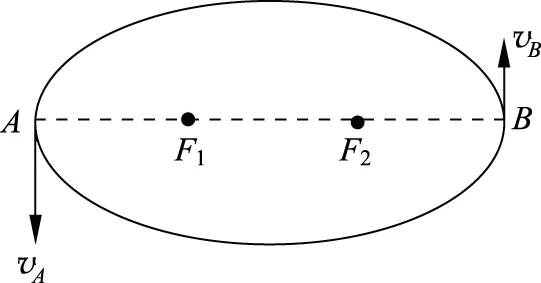
图 5

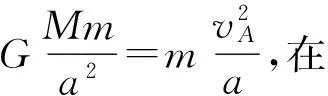
在纠正学生错误过程中，还可以采用一题多解的方法，一方面从另一个角度验证解的正确性，加深学生对概念的理解；同时也提高了多角度考虑问题的能力，在建模时更加准确与迅速。例如本题还可以这样解：

图 6

2) 拓展深化物理模型，促进物理模型的系统化

有意识地向学生提供更为广阔的背景材料，通过在新颖情境中应用知识，以衬托模型、突出模型、拓展模型，可以使学生的知识结构和认知结构更加丰富和完善，更趋系统化[3]。

案例分析5

对于单摆模型的教学在进行基本应用练习后，可以进一步提出下列两个层次的问题以拓展学生对单摆模型的认识。

① 如图7所示，当把一摆长为L，周期为T的单摆放在加速度为a的匀加速上升的电梯中，其单摆周期会变为多少？若电梯以加速度a加速下降，情况又如何？当电梯做自由落体运动时，又如何呢？

② 如图8是记录地震装置的水平摆，摆球m固定在边长为L，质量可忽略不计的等边三角形的顶点A上，它的对边BC跟竖直线成不大的夹角α，摆球可绕固定轴BC摆动，求摆球作微小摆动的周期。

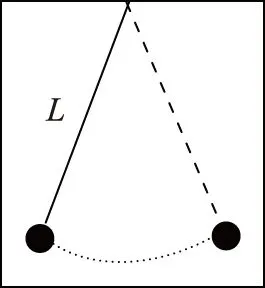
图 7

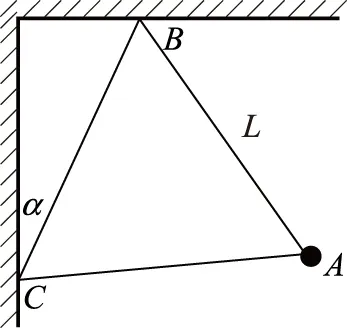
图 8

分析与解： 对于异型摆而言，其等效摆长和等效重力加速度就要依不同的情况具体分析了。我们只要找准了类似单摆的摆长及对应的重力加速度，亦即找准等效摆长和等效重力加速度，问题就迎刃而解了。

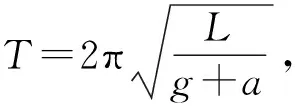
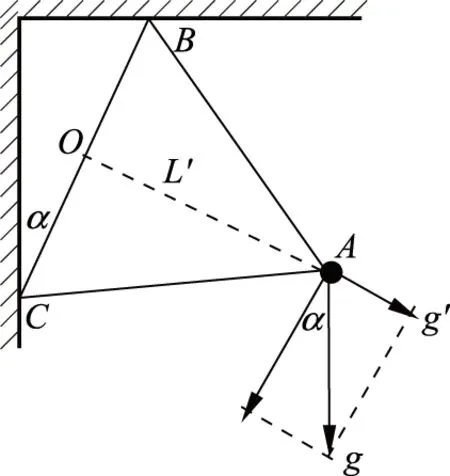
图 9

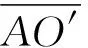
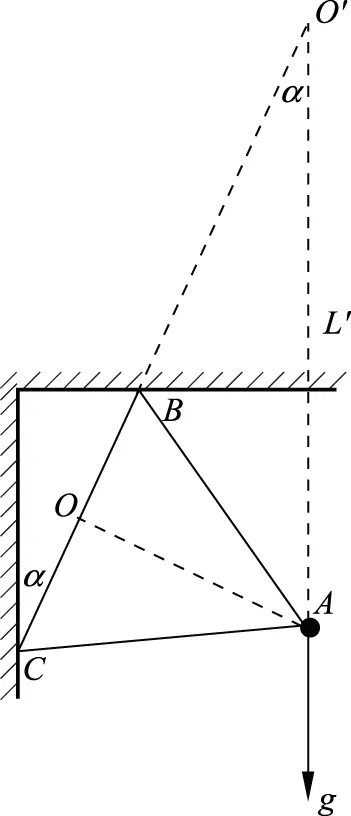
图 10

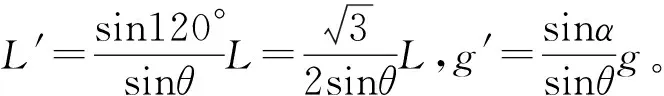
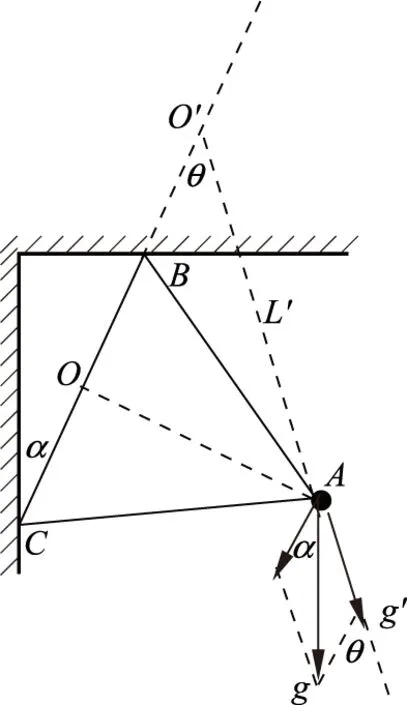
图 11

通过这样一系列具有一定广度和深度的问题启发学生进行分析、综合、类比和推理等思维活动，不但可以深化对“单摆”模型的理解，而且锻炼了学生分析、解决问题的能力。

总之，物理模型是抽象思维的产物，加强物理模型的建立、识别和应用的教学是提升学生抽象思维能力的重要途径。实际上，每个学生头脑中都有物理模型，但就是储存的量和质上存在着很大的差异，优秀学生头脑中的物理模型存储量多而且清晰、深刻，遇到问题很快就可以将问题进行肢解，迅速识别出问题中所包含的物理模型。物理模型教学的任务就是要加强模型的有意识的培养和训练，不断提升学生抽象思维的能力。

[1] 阎金铎.物理思维论[M].南宁：广西教育出版社，1996：181.

[2] 钟小平.类比法在高中物理教学中的运用[J].物理教学,2013(9). Zhong Xiaoping. The application of analogy method in Physics Teaching in Senior High School[J]. Physics Teaching, 2013(9). (in Chinese)

[3] 赵君武.物理理想模型的教学策略[J].陕西师范大学学报(哲学社会科学版).2000(5). Zhao Junwu. Teaching strategies of physics ideal model[J]. Journal of Shaanxi Normal University (Philosophy And Social Sciences). 2000(5). (in Chinese)

STRENGTHENING THE TEACHING OF PHYSICAL MODEL TO
IMPROVE STUDENTS’ ABSTRACT THINKING ABILITY

Xu Bin

(Changzhou No.1 High School, Changzhou Jiangsu 213003)

Physical model is a product of abstract thinking, which is a highly abstract and idealized thinking object from the prototype established by people to engage in the research. Profundity and flexibility of abstract thinking reflect the students’ thinking quality. Through the strengthening of physical model teaching, students can eliminate thinking obstacles, overcome mindset, and strengthen training of thinking, which is beneficial for them to enhance the ability of abstract thinking.

physical model; abstract thinking

2016-05-06；

2016-08-11

徐斌，男，高级教师，主要研究方向为高中物理课堂教学设计，全国高中物理竞赛，xubinphy@sina.com。

徐斌. 加强物理模型教学 提升学生抽象思维能力[J]. 物理与工程，2017，27(2)：71-76.