Mathematica在普通物理教学中的应用

刘 鑫 赵里昂 于文晶 杨华哲

(中国医科大学公共基础学院物理与生物物理教研室, 辽宁 沈阳 110122)

Mathematica在普通物理教学中的应用

刘 鑫 赵里昂 于文晶 杨华哲

(中国医科大学公共基础学院物理与生物物理教研室, 辽宁 沈阳 110122)

目的：针对高校普通物理的传统课堂教学内容抽象复杂，教学方式较大局限性及学生吸收知识慢、兴趣弱等问题，可适当引入计算机软件支撑教学，丰富课堂，解决以上教学难题。方法：运用Mathematica软件的强大动画和绘图功能，对普通物理教学中振动和波的几个典型问题进行分析。结果：通过将教学软件Mathematica与基础物理知识的讲授教学有机结合，可以将课堂中原始化手工推算的内容直观图像化、动画化，令学生更直观地理解课堂内容。结论：通过对实例的阐述可以看出，将Mathematica引入教学能够帮助学生更快、更好地理解物理知识，同时激发学生对物理知识的浓厚兴趣，培养学生的独立思考能力，使课堂教学更高效。

Mathematica；普通物理；教学模式

在普通物理知识的教学过程中, 包含力学、热学、光学、电磁学等课程. 其中不乏些复杂抽象的物理问题, 原始课堂教学虽有多媒体课件等教学手段, 依然无法避免应用手工推算的方法让学生理解物理规律, 在这种枯燥的教学模式下, 学生即使可以得到解析结果, 却不易得到直观的物理图像, 很大程度抑制了学生的学习兴趣. 与此同时, 由于课堂教学的时间局限性, 需要学生在很短的时间内快速对较多的抽象理论进行推算和深入理解, 并完成许多基于高等数学的高等运算,已经成为高校普通物理的教学瓶颈。为了解决上述问题, 国内许多高校开始引入教学软件来丰富学生对普通物理知识的直观理解, 目前Matlab、Maple、 Mathematica、MathCAD等几大数学软件工具可以有效地与理论知识教学相结合, 达到较好的课堂教学效果。其中Mathematica作为一个著名的数学软件, 相对其他教学软件更加小巧方便。Mathematica主要是由美国Wolfram公司研究开发, 可用来从事数值、符号的相关运算,拥有从多项式运算到微积分、特殊函数分析运算等丰富的功能。与Matlab等软件相比, Mathematica在无需掌握C语言或Fortran等复杂计算机语言条件下即可满足物理教学中对完成数学图形绘制，甚至动画制作等多种需求，避免了漫长的熟练计算机语言过程。此外，Mathematica在一个notebook里面即可把公式文档和计算过程一一表达, 拥有简单语法却可实现强大功能, 这在此类软件中非常难得。因此, 如将Mathematica适当地引入普通物理的教学, 在进行简单的学习教程后就可编程出需要的教学内容, 即可将原本复杂的原始化手工推算用Mathematica作图来给学生以直观展示, 也可快速编译出抽象物理理论的动画来推进课程进行, 激发学生对原本枯燥复杂的物理规律的学习兴趣, 这样既可以节省课堂时间来进行原本的手工推算, 又会使学生快速吸收普通物理的理论知识, 提高课堂授课效率。通过借助此类计算软件实现物理理论的可视化教学，对于探索新型的高效课堂教学具有重要的意义。

1 应用举例

普通物理中涉及许多知识, 此处针对机械运动和机械波部分进行举例。与一些物理理论相似, 振动和波经常涉及复杂的数学运算, 因此可在教学中引入Mathematica绘制出生动精美的波形与动画, 丰富课堂教学, 可以起到事半功倍的效果。

1.1 振动的合成图形

由于振动的合成多种多样, 书本和手工演算很难为学生建立形象、直观的物理模型，影响了学生对于知识的理解。由于Mathematica软件有强大的动态图形演示功能, 所以在教学过程中, 适当穿插动态图形演示很必要。

1.1.1 两个同方向同频率的简谐振动的合成图像

两个同方向同频率的简谐振动合成之后仍为简谐振动, 频率不变。令两个分振动分别为y1=A1cosωt和y2=A2cos(ωt+2πφ), 合振动则是二者之和, 其中ω=1rad·s-1,笔者在软件中将φ取值范围定义在0到1之间, 可在软件运行过程中改变数值观察图像, 分振动的振幅A1可取值为1、2, 振幅A2可取值为0、1、2, 然后将3条简谐振动的曲线在同一坐标中体现。

运行命令如下

Manipulate[Plot[{A1 Cos[t], A2 Cos[t+2 Pi phi], A1 Cos[t]+A2 Cos[t+2 Pi phi]}, {t, 0, 4 Pi}, Frame -> True, PlotRange -> 4, PlotStyle -> {Dashed, Green, Blue}, PlotLegends -> {"SBM1", "SBM2", "SBM1+SBM2"}],{phi, 0, 1}, {A1, {1, 2}}, {A2, {0, 1, 2}}]

运行后可以在统一坐标中得到3条简谐振动的曲线, 并可以通过改变各分振动的振幅, 得到对应的简谐振动图像, 图1展示了程序通过改变振幅值而得到的瞬时简谐振动图像。图2展示了程序通过改变某分振动φ的取值范围定义所得到的瞬时简谐振动图像.

1.1.2 两个方向垂直的简谐振动的合成图像——李萨茹图形

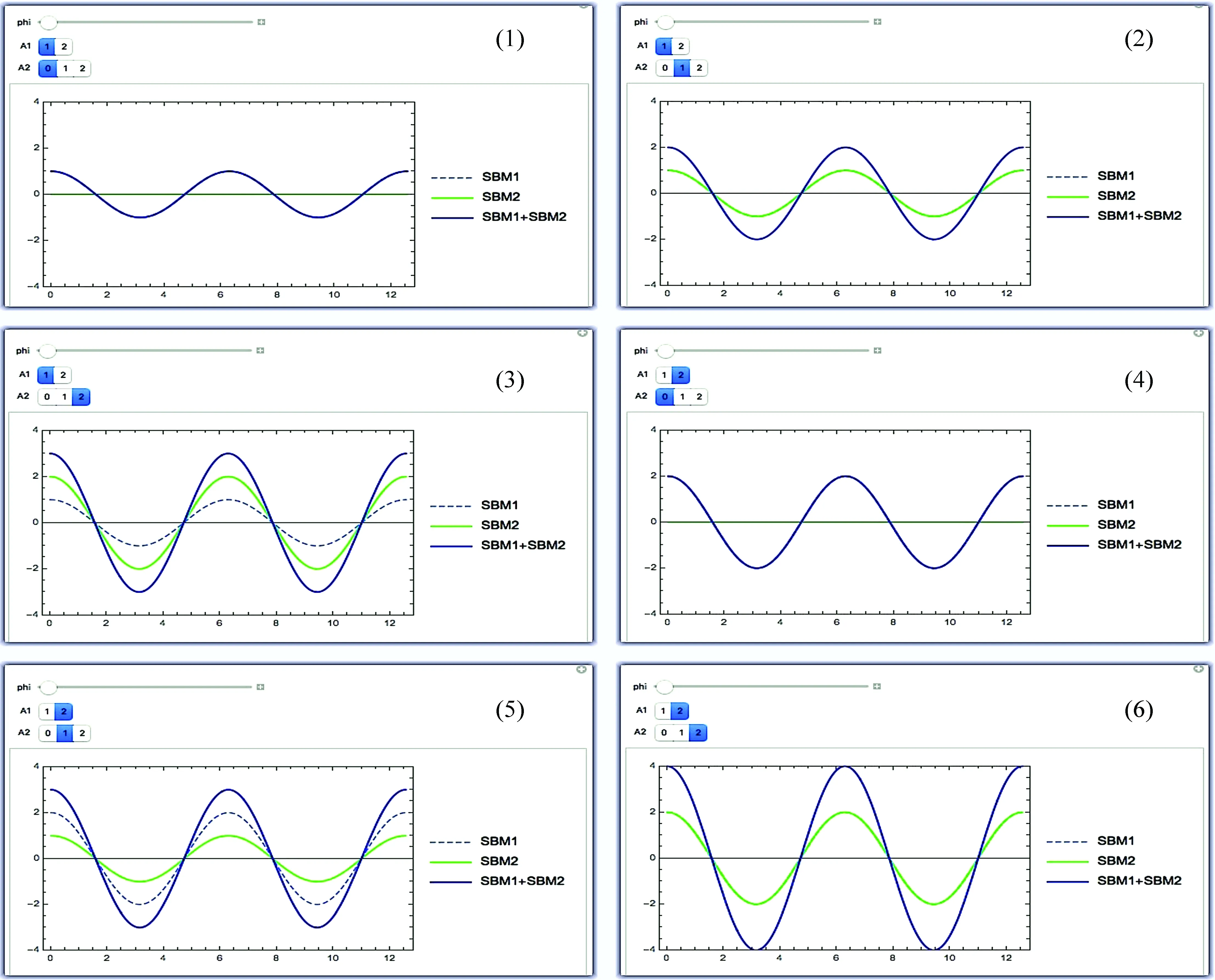
图1 简谐振动图像(1) 振幅A1=1的分振动瞬时简谐振动图像; (2) 振幅A1=1、A2=1的分振动合成后的瞬时简谐振动图像； (3) 振幅A1=1、A2=2的分振动合成后的瞬时简谐振动图像； (4) 振幅A1=2的分振动瞬时简谐振动图像； (5) 振幅A1=2、A2=1的分振动合成后的瞬时简谐振动图像； (6) 振幅A1=2、A2=2的分振动合成后的瞬时简谐振动图像

图2 某分振动改变相位时的合简谐振动瞬时图像对比

两个方向垂直的简谐振动可以合成各种奇特的曲线图型, 由在互相垂直的方向上的两个频率成简单整数比的简谐振动所合成的规则的、稳定的闭合曲线被称为李萨茹图形。在此理论基础上, 使用李萨茹图形可以测量出两个信号的频率比与相位差, 常利用的工具是示波器, 并用以测定频率或相位差。

如两个简谐振动方程分别为x=cosωt和y=cos(ωt+φ),通过对ω和φ的赋值,分别针对两个分振动振幅相同时和振幅成比例时的合成情况, 使用Mathematica的命令进行质点运动的动态演示, 并配以合成运动的稳定轨迹图, 命令语句如下：

w=2/3; phi=Pi/4;

{Button["1.0", w=1; phi=0 Pi;],

Button["1.1/6", w=1; phi=Pi/6;],

Button["1.1/4", w=1; phi=Pi/4;], Button["1.1/3", w=1; phi=Pi/3;],Button["1.2/3", w = 1; phi = 2 Pi/3;], Button["2.0", w=2; phi = 0 Pi;], Button["2.1/4", w=2; phi=Pi/4;], Button["2.1/2", w=2; phi=Pi/2;], Button["3.1/2", w=3; phi=Pi/2;], Button["1.5.1/4", w=1.5; phi=Pi/4;], Button["1.5.1/2", w=1.5; phi=Pi/2;], Button["2.5.1/4", w=2.5; phi=Pi/4;], Button["2.5.1/2", w=2.5; phi=Pi/2;]}

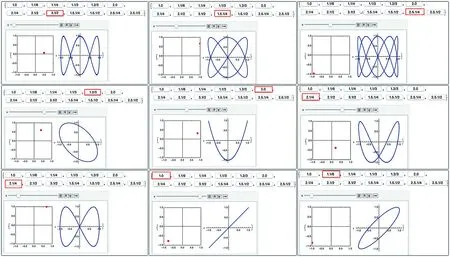
图3 Mathematica动画运行的部分图形

Animate[{ParametricPlot[{Cos[t], Cos[w t+phi]}, {t, u, u+0.01}, Mesh -> {Range[u, u+0.01]}, MeshStyle -> {Red, PointSize[Large]}, Frame -> True, PlotRange -> 1], ParametricPlot[{Cos[t], Cos[w t+phi]}, {t, 0, 10 Pi}]}, {u, 0, 10 Pi}, AnimationRunning -> False]

1.2 惠更斯定理的图形演示

图4 缝半宽时单缝衍射下的惠更斯定理动画瞬时图像

惠更斯原理是一种用来分析、解释波动如何行进的理论. 惠更斯认为, 波在传递过程中, 波前上任何一点都可视为一个新的点波源, 这些点波源将会往前进的方向产生新的波, 而波的下一时刻的波形便是由这些点波源波形叠加合成的结果。我们使用惠更斯原理解释波的衍射现象, 发现平面波在到达一宽度与波长相近的缝时, 缝上各点都可以看做新的波源, 做出它们的包络就可以得到新的波前, 此时波可以绕过障碍物向前传播, 不过此时平面波的形状发生改变, 边缘处会发生波前弯曲. 并且缝的宽度相对波长越小, 衍射现象越明显. 运用Mathematica命令制作动画, 改变缝的宽度来演示惠更斯定理, 其中图4展示了动画运行过程的部分图形, 可让学生快速理解知识。运行如下命令：

{Button["0.5", {l=0.5, p=0.125}], Button["1", {l=1, p=0.25}], Button["2", {l=2, p=0.5}], Button["4", {l=4, p=1}]}

Animate[

Graphics[

Table[Circle[{n, 0}, t, {0, Pi}], {n, -l, l, p}], Axes -> True, PlotRange -> {{-7, 7}, {-0.2, 2 Pi}}, Frame -> True,

FrameTicks -> {{{-2 Pi, -Pi, 0, Pi, 2 Pi}, None}, {{-6, -4, -2, 0, 2, 4, 6}, None}}, Epilog -> {Rectangle[{-7, 0}, {-l, -0.2}], Rectangle[{7, 0}, {l, -0.2}]} ], {t, 0, 2 Pi}]

2 结语

利用先进的软件Mathematica, 可以通过简单的计算机语言, 直观生动地展示出物理图像, 让学生可以在简短的课堂教学中, 更快速地明确普通物理的相关知识, 激发学生的学习热情。现代化教学需要教师解放教学思想, 开拓思路, 适当地利用多媒体软件及计算软件辅助教学, 通过教学模式的创新提高教学效率。本文中笔者只是应用Mathematica的强大的动画绘图功能, 还有许多丰富的功能等待利用。在当下的信息时代, 希望有更多的高校教师能更加有效地利用不同软件, 恰当地将普通物理的知识学习与其结合, 共同 促进新型普通物理教学模式的发展。本文中的所有程序运算全部在Mathematica软件官方云网站平台(http://develop.open.wolframcloud.com/app/)进行。

[1] 鲍四元,孙洪泉,陈旭元.Mathematica在振动波问题中的应用[J].物理与工程,2010,20(4):49-51,64. Bao Siyuan, Sun Hongquan, Chen Xuyuan. Application of Mathmatica in the vibration wave problems[J]. Physics and Engineering, 2010, 20(4): 49-51, 64. (in Chinese)

[2] 柴连明,高伟.Mathematica与基础物理教学[J].无线互联科技,2014(7):257-258. Chai Lianming, Gao Wei. Mathematica and basic physics teaching[J]. Wireless Internet Technology, 2014(7): 257-258. (in Chinese)

[3] 洪洋.医用物理学[M].北京:高等教育出版社,2014.

[4] Wolfman S. Mathematica全书(特别版)[M].周孝方译.西安:西安交通大学出版社,2002.

[5] 韩克祯,耿雪.Mathematica软件在波动教学中的应用[J].物理通报,2013(3):70-72. Han Kezhen, Geng Xue. The application on Mathematic in wave teaching[J]. Physics Bulletin, 2013(3):70-72. (in Chinese)

[6] 张新,倪致祥.基于Mathematica的振动传播演示[J].阜阳师范学院学报：自然科学版,2008,25(2), 31-33. Zhang Xin,Ni Zhixiang. Vibration propagation’s demonstration based on Mathematica[J]. Journal of Fuyang Teachers College(Natural Science),2008,25(2), 31-33. (in Chinese)

APPLICATIONS OF MATHEMATICA IN GENERAL PHYSICS TEACHING

Liu Xin Zhao Li’ang Yu Wenjing Yang Huazhe

(Department of Physics and Biophysics, School of Fundamental Sciences, China Medical University, Shenyang Liaoning 110122)

Traditional teaching method of general physics in colleges and universities is abstract and complicated, which is limited and unfavorable for the comprehension of knowledge and interests in learning for most students. As a potential solution, the application of some computer software in teaching is considered to overcome the above-mentioned problems by enriching the classes. We analyzed some typical physical cases on vibration and waves via Mathematica by using the powerful animation and drawing function of the software. The calculated content would be more intuitive visualization, animation and intuition in the teaching through the combination of Mathematica and the traditional teaching method of basic physics knowledge. It would be helpful for students to get better and faster understanding of physical theories by introducing Mathematica into physics teaching. In addition, it can stimulate a lot of interests of studentsin physics knowledgeand cultivate theirability of independent thinking, which also promotes the efficiency of classroom teaching.

Mathematica; general physics; teaching method

2016-10-19

国家自然科学基金(编号：81500897)；国家留学基金(编号：201408210385)；辽宁省教育厅一般项目(编号：L2013285)。

刘鑫，女，助教，主要从事物理学的科研与教学研究,xliu13@cmu.edu.cn。

杨华哲，男，副教授，主要从事物理学的科研与教学研究,hzyang@mail.cmu.edu.cn。

刘鑫，赵里昂，于文晶，等. Mathematica在普通物理教学中的应用[J]. 物理与工程，2017，27(2)：51-55.