雷达高度计海况偏差估计神经网络模型研究

郭迎婷，苗洪利*，张国首，荆玉洁，王桂忠

(1.中国海洋大学 信息科学与工程学院，山东 青岛 266100)



雷达高度计海况偏差估计神经网络模型研究

郭迎婷1，苗洪利1*，张国首1，荆玉洁1，王桂忠1

(1.中国海洋大学 信息科学与工程学院，山东 青岛 266100)

本文基于Jason-2高度计数据，在12个不同季节的cycle数据中组合1～6个cycle的有效波高、风速和海况偏差为训练集，选取Jason-2的另外3个不同季节的cycle数据集为测试集。经检验分析，确定3个cycle对应的BP神经网络模型。将该模型应用于HY-2高度计海况偏差的估计，通过海况偏差与有效波高及风速的拟合优度、解释方差和残差对比分析，结果表明：神经网络BP模型可以有效应用于HY-2的海况偏差估计并明显优于传统海况偏差参数模型。

雷达高度计；海况偏差；神经网络模型；有效波高；风速

1 引言

卫星雷达高度计可以快速准确测得全球海表面高度(SSH)、有效波高(SWH)以及风速(U)等信息。随着精密定轨技术的发展，海况偏差(SSB)已取代轨道误差成为测高的第一误差源[1-2]。SSB估计目前分为理论模型和经验模型，但由于理论模型难以获得所需参数无法实用[2]。目前普遍适用的经验模型分为参数模型[3-4]、非参数模型[5-6]和直接估计方法[7]。但是由于参数模型的精度受限、非参数模型与直接估计的外延性受限，在使用中均存在一定误差。

1986年，McCleland和Romelhart提出多层前馈网络训练的BP神经网络模型，该模型采用误差反向传播算法。这种人工神经网络模型具有大规模并行数据处理、分布式存储和良好容错性特点，同时其自适应性和自组织性也较强[8]。

本文将BP模型应用于雷达高度计的的海况偏差估计。采用雷达高度计Jason-2 GDR数据集中不同季节的12个cycle并组合1～6个cycle数据，使用其SWH、U、SSB作为训练集，并以其SSB值为真值。同时使用另外3个不同季节的cycle数据作为测试集，通过对比其解释方差(D)、标准差(S)及残差分析，选择最优数据集大小，得到最优的海况偏差SSB估计BP网络模型。并将最优BP模型应用于HY-2高度计。

2 建模原理

人工神经网络模型种类较多，目前应用最为广泛的为BP网络模型。一个典型的3层BP网络结构如图1所示，其包含输入层、隐含层、输出层。层与层之间采用全互连方式，同一层之间不存在相互连接，隐含层可以一层也可以多层。学习训练过程分为信号的正向传播以及误差的反向传播过程[9]。信号正向传播时，训练集通过输入层输入，经由各隐含层逐个神经元处理，传向输出层。每层神经元的状态只影响下一层神经元状态。如果训练所得实际输出与期望输出不符，就进入误差反向传播阶段[10]。误差信号沿原来连接通路返回，逐次调节各层连接权值与阈值，直至到达输入层。信号正向传播和误差反向传播两个过程一直反复进行，直到网络的输出误差最小或者其迭代次数达到预期设定值，学习训练过程结束，模型建立完成[10]。

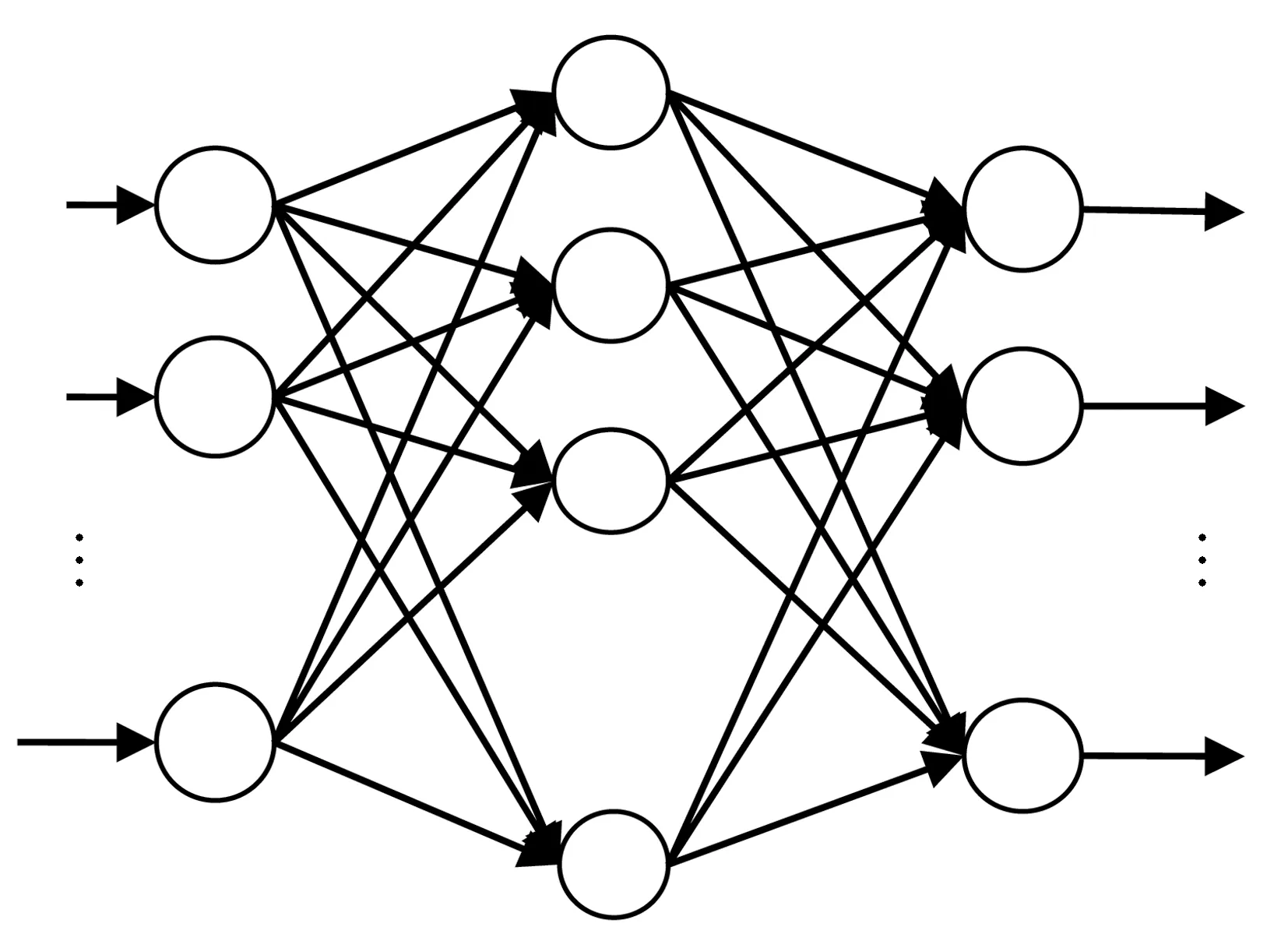
图1 三层神经网络Fig.1 Three layer back-propagation network

本文采用3层BP网络模型，设其输入、隐含和输出层节点数分别为n、m、q。Xi表示样本的第i个输入值，ωki表示输入层第i个节点到隐含层第k个节点的权值，ωjk表示隐含层第k个节点到输出层第j个节点的权值[11]。其权值表达形式为：

(1)

为方便起见，将阈值写入连接权当中，则隐含层第k个节点的输出为：

(2)

输出层第j个节点的输出为：

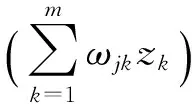
输入层到隐含层的非线性传递函数f为tansig，其表达式为：

(4)

隐含层到输出层的线性传递函数f为purelin，其表达式为：

f(x)=k·x+b，

(5)

式中，k为任意不为零实数，b为任意实数。

训练函数采用Levenberg-Marquardt反向传播算法。

全局误差函数为：

(6)

式中，M为样本总数，tpj为期望输出。

BP模型的权值调整公式为：

(7)

其中η∈(0,1)为学习率。

3 模型建立

3.1 建立数据集

本文采用Jason-2高度计2014、2015年不同月份的12个cycle数据。根据Jason-2数据手册的要求[12]，对高度计测高数据添加除SSB之外的仪器误差、干和湿对流层延迟、电离层延迟及大气逆压、高频振荡、潮汐、极潮、固体地球潮、负荷潮等误差校正项，并剔除SWH<0 m或SWH>10 m、U<0 m/s或U>10 m/s以及SSB>0 m或SSB<-0.5 m的异常数据，并将数据集进行归一化处理[13]。为确定最优数据集大小，根据季节分布分别组合1个cycle、2个cycle、3个cycle、4个cycle、5个cycle、6个cycle的数据集，其大小分别为347 986、749 165、1 158 873、1 592 432、2 006 952、2 384 973。将SWH、U作为训练集的输入，SSB作为期望输出，分别训练学习模型。同时选取训练集没有使用的243、255、267cycle且同样分布在不同季节(2015年2、6、10月份)的数据作为测试集，对比不同大小数据集所训练模型应用于同一测试集的解释方差(D)、标准差(S)及残差分析，从而确定最优数据集大小并建立BP模型。

3.2 BP模型建立

BP网络模型设计为3层(图2)。输入层两个节点为SWH、U，输出层一个节点为SSB。隐含层节点数的确定是一个复杂的问题，至今尚未有一个很好的经验解析式。隐含层的节点数由函数的复杂程度决定，太多会导致网络学习时间过长，太少则导致容错性太差、识别未经学习的样本能力太低。根据前人经验，隐含层节点的选择依据参考公式：

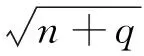
(8)

图2 BP模型结构Fig.2 Back-propagation model structure

3.3 BP模型优选及检验

基于以上BP模型，通过选用不同数据集大小学习训练模型，并在同一测试集中分别计算S、D，以确定最优BP模型。

标准差(S)：

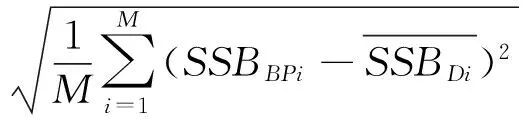
(9)

式中，M为测试数据集大小，SSBBPi为BP模型所得SSB估计值，SSBDi为随测试数据集发布的GDR数据。

(10)

其S、D值计算结果如表1，变化曲线如图3所示。

表1 不同周期数的D、S值

图3 D、S变化曲线Fig.3 D and S curve

D以及S随着周期数的变化呈现一定的变化趋势，D值用来评价模型的有效性，其值越大说明模型越有效[13]。S值表示BP模型测试所得SSB估计值与原有GDR中SSB估计值的偏差，其值越小说明差异越小。

从表1和图3可以看出，6组训练数据集对同一测试集的结果差距并不是很大，原因是随着数据集的增大，D和S趋于平稳，即使1个cycle的数据也达到347 986个，已满足BP网络建模要求。最终选用3个cycle的数据建立的模型，D和S值略小，同时数据季节分布更具代表性(221cycle：2014年7月；239cycle：2014年12月；245cycle：2015年3月)。

表1中，3个cycle训练集所建立的BP模型结果与GDR值(视为真值)的标准差为0.77 cm，差值ΔSSB=SSBGDR-SSBBP密度分布如图4所示，二者拟合散点图如图5所示。可以看到，十分趋于一致，说明所建BP模型具有较好的有效性和准确性。

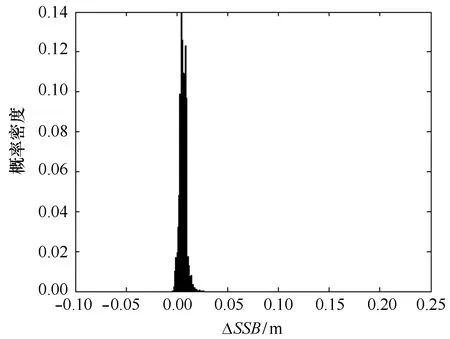
图4 ΔSSB的概率密度分布图Fig.4 Probability density distribution map of ΔSSB

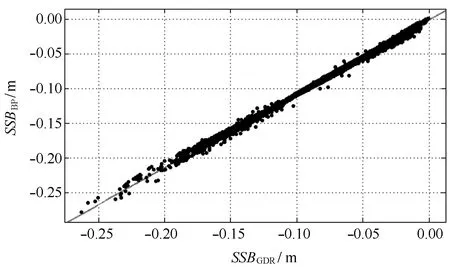
图5 SSBBP与SSBGDR拟合散点图Fig.5 SSBBP and SSBGDR scatter plot

4 模型应用与分析

将以上所确定的BP网络模型应用于HY-2高度计第70cycle数据。HY-2的SSB估计采用传统参数模型，将BP模型结果与HY-2中GDR参数模型结果进行差异分析、SSB与SWH和U的拟合优度、解释方差及残差分析，用以进一步验证BP模型的有效性。

4.1 两模型SSB差异分析

将BP模型所得的SSB结果与HY-2的GDR中SSB值进行比较，二者之差(ΔSSB=SSBGDR-SSBBP)的密度分布如图6所示，拟合散点图如图7所示。

图6 ΔSSB的概率密度分布图Fig.6 Probability density distribution map of ΔSSB

图7 SSBBP与SSBGDR拟合散点图Fig.7 SSBBP and SSBGDR scatter plot

通过公式(9)计算得出标准差S为2.98 cm，BP模型SSB平均绝对值为3.29 cm，而GDR的SSB平均绝对值为2.25 cm。结合图6分析，BP模型的SSB估计平均绝对值高于传统参数模型SSB估计平均绝对值1.04 cm，相对偏差31.56%，且差值大部分集中在-1～4 cm之间，占整体数据的92.56%。说明BP模型结果与GDR中的SSB结果整体符合度较好，但确实存在一定的差异。

从图7可以看出，BP模型SSB结果与GDR的SSB结果基本呈线性正相关，但拟合直线的斜率并不为1。在-0.05 m附近二者结果接近，绝对值小于0.05 m时，GDR的SSB绝对值略大，而绝对值大于0.05 m时，GDR的SSB绝对值偏小，而从图5分析，模型结果与测试集的真值之间并不存在这样的趋势，只能说明GDR中的SSB值(传统参数模型)存在偏差，特别在SSB绝对值趋向较大时，这种偏差逐渐变大。

4.2SSB与SWH和U的拟合优度分析

模型的建立是基于SSB与SWH和U的相关这个基本假设。因此，SSB与SWH和U的相关度越高，残差就越小，说明模型越有效。

图8 SSBBP与SWH拟合散点图Fig.8 SSBBP and SWH scatter plot

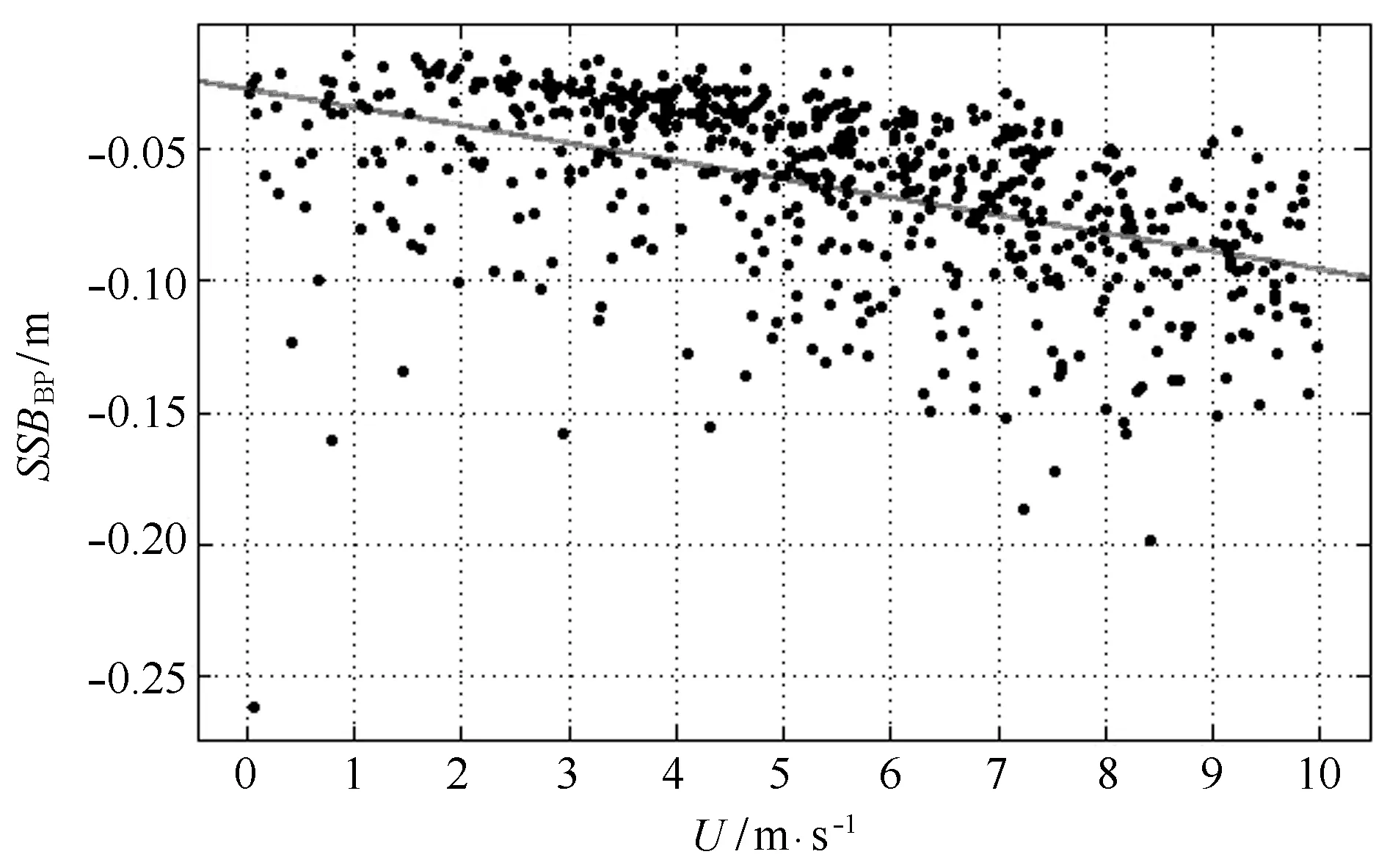
图9 SSBBP与U拟合散点图Fig.9 SSBBP and U scatter plot

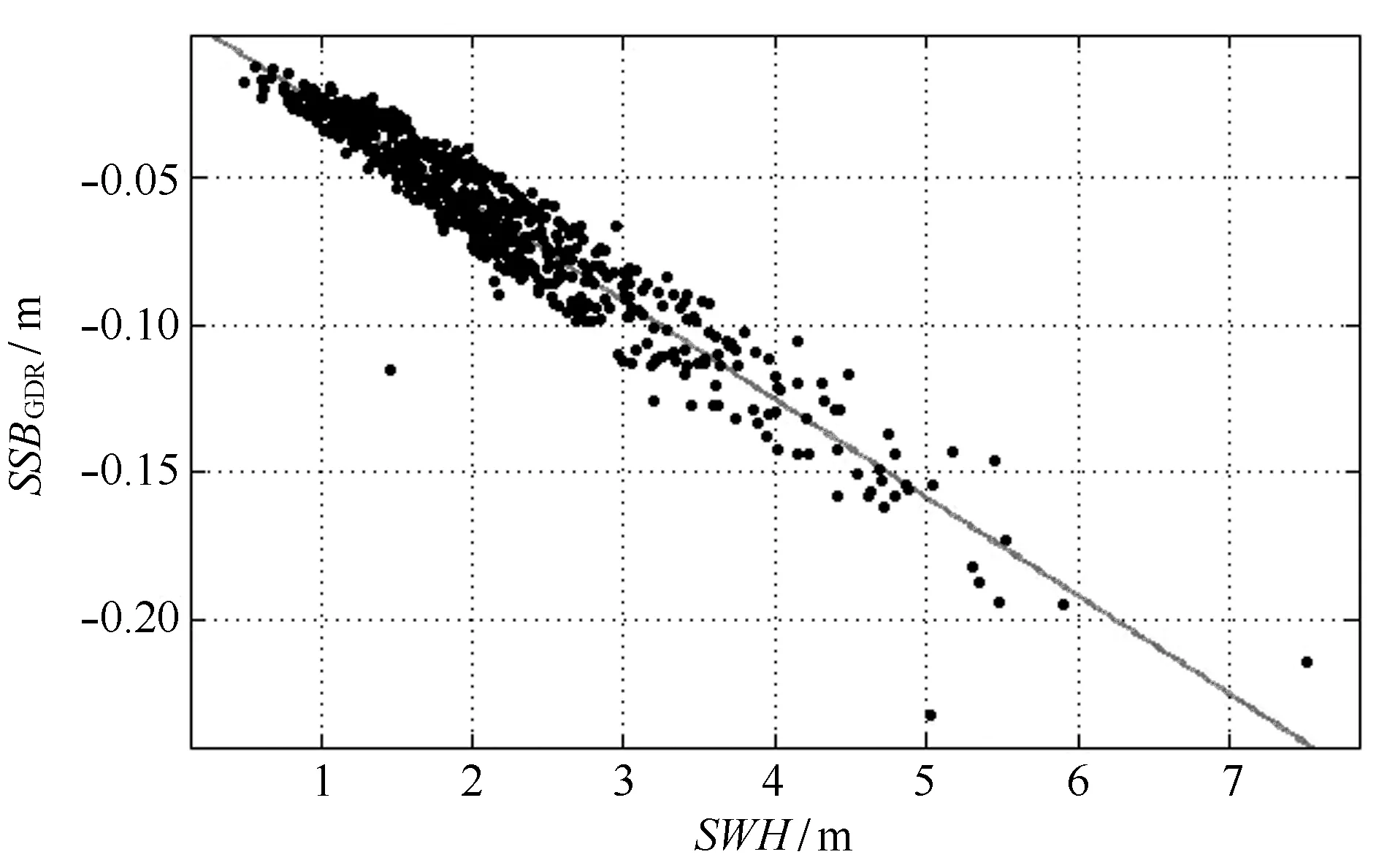
图10 SSBGDR与SWH拟合散点图Fig.10 SSBGDR and SWH scatter plot

图11 SSBGDR与U拟合散点图Fig.11 SSBGDR and U scatter plot

4.3 解释方差分析

通过提取HY-2第70cycle 624组交叉点数据，分别用BP模型与原有GDR参数模型SSB结果对交叉点处上升轨和下降轨的SSH校正。经计算得到BP模型解释方差DBP=29.26 cm2， GDR中参数模型的解释方差DGDR=27.61 cm2，由此可见，BP神经网络模型较参数模型更为有效。

4.4 残差分析

在HY-2第70cycle 624组交叉点数据上，两个模型结果分别做残差与有效波高和风速的相关分析，残差的计算如式(11)。

ε=ΔSSH′-ΔSSB=

(11)

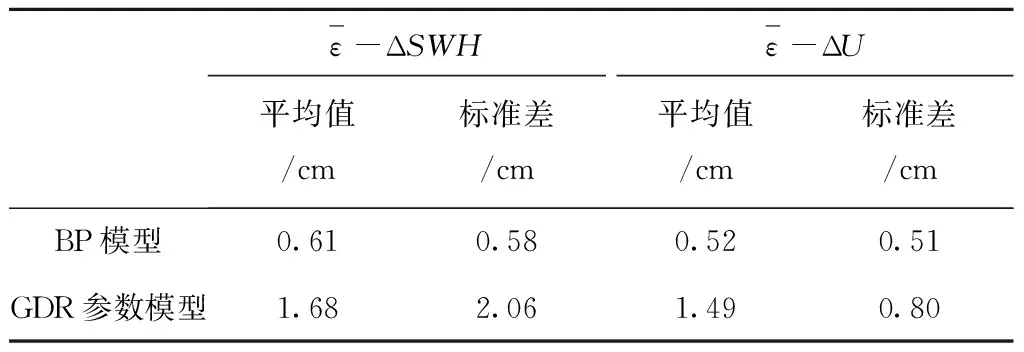
表2 BP神经网络模型、GDR中参数模型结果及检验

图随ΔSWH变化

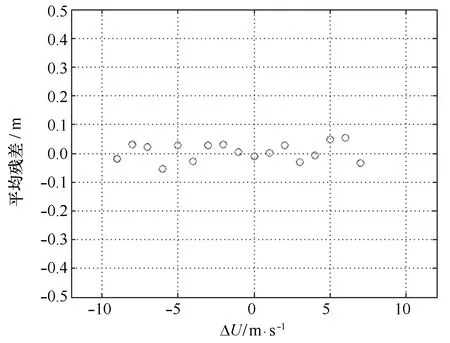
图随ΔU变化

图随ΔSWH变化

图随ΔU变化

无论从表2的统计数据还是从残差分布图均可以看出，BP模型相比传统的参数模型更具有效性。

5 结论

本文基于Jason-2高度计数据，在12个不同季节的cycle中通过组合1～6个cycle数据集训练BP网络模型，分别在另外3个cycle组成的测试集检验分析，验证了模型的有效性和准确性并确定3个cycle的数据集建模为最终BP模型。将所建BP模型应用于HY-2高度计第70cycle，HY-2自身GDR发布的SSB是传统经验模型获得。经对比，BP网络模型SSB输出结果与自身GDR中SSB的标准差S为2.98 cm，平均绝对值高出1.04 cm，表明存在明显差异。BP模型SSB与SWH和U的拟合优度为0.97和0.23；而GDR中SSB与SWH和U的拟合优度为0.90和0.21，将BP模型运用在第70cycle交叉点数据集，其解释方差为29.26 cm2，而GDR中SSB的解释方差为27.61 cm2，从模型残差统计和分布分析同样可以看到基于Jason-2数据集建立的BP网络模型可以有效应用于HY-2高度计的SSB估计，并明显优于传统经验模型，能够有效提高海表面高度校正水平。

[1] Elfouhaily T， Thompson D R， Chapron B， et al. Improved electromagnetic bias theory[J]. Journal of Geophysical Research， 2000， 105(C1): 1299-1310．

[2] Fu L L， Cazenave A. Satellite Altimetry and Earth Sciences: A Handbook of Techniques and Applications[M]. San Diego: Academic Press， 2001：1-4．

[3] Zhang Guoshou， Miao Hongli， Wang Guizhong， et al. Study on parametric models of estimating the sea state bias based on the HY-2 altimeter[C]//IEEE International Congress on Image and Signal Processing. 2015：1100-1104．

[4] Zhou Xiaoguang, Miao Hongli, Wang Yahui， et al. Study on the determination of crossovers by piecewise fitting of satellite ground track[J]. Acta Geodaetica et Cartographica Sinica， 2012， 41(6): 811-815．

[5] Gaspar P， Labroue S， Ogor F， et al. Improving nonparametric estimates of the sea state bias in radar altimeter measurements of sea level[J]. Journal of Atmospheric & Oceanic Technology， 2002， 19(10): 1690-1707．

[6] Labroue S， Gaspar P， Dorandeu J， et al. Nonparametric estimates of the sea state bias for the Jason-1 radar altimeter[J]. Marine Geodesy， 2004， 27(3): 453-481．

[7] Vandemark D， Tran N， Beckley B， et al. Direct estimation of sea state impacts on radar altimeter sea level measurements[J]. Geophysical Research Letters， 2002， 29(24): 48-52．

[8] Li Ruping， Zhu Lian， Wu Fangshen， et al. BP neural network algorithm improvement and application research[J]. Journal of Heze University， 2016，38(2)：13-17．

[9] Xiao Zhi, Ye Shijie, Zhong Bo, et al. BP neural network with rough set for short term load forecasting[J]. Expert Systems with Applications, 2009, 36(1):273-279.

[10] 王晶晶，王剑.一种BP神经网络改进算法研究[J].软件导刊，2015(3):52-53．

Wing Jingjing， Wang Jian. Research on an improved algorithm of back-propagation neural network[J]. Software Guide， 2015(3):52-53．

[11] 李书光， 王云海， 苗洪利， 等. 基于JASON-1高度计的海况偏差校正参数模型[J]. 中国石油大学学报(自然科学版)， 2013， 37(2):181-185．

Li Shuguang， Wang Yunhai， Miao Hongli， et al. Sea state bias correction parameter model based on JASON-1 altimeter[J]. Journal of China University of Petroleum(Natural Science Edition)， 2013， 37(2):181-185．

[12] 王桂忠， 苗洪利， 王鑫， 等. 基于共线和交叉点融合数据的高度计海况偏差参数模型的研究[J]. 遥感技术与应用， 2014， 29(1):176-180．

Wang Guizhong， Miao Hongli， Wang Xin， et al. Study on the altimeter sea state bias parameter model of data fusion based on collinear and crossover[J]. Remote Sensing Technology and Application， 2014， 29(1):176-180．

[13] 苗洪利， 王鑫， 王桂忠， 等. 改进的高度计海况偏差估计参数模型研究[J]. 中国海洋大学学报(自然科学版)， 2015， 45(12):119-124．

Miao Hongli， Wang Xin， Wang Guizhong， et al. Study on parameter estimation of altimeter sea state bias improved[J]. Journal of Ocean University of China(Natural Science Edition)， 2015， 45(12):119-124．

Study on neural network model of estimating the sea state bias for radar altimeters

Guo Yingting1， Miao Hongli1， Zhang Guoshou1， Jing Yujie1， Wang Guizhong1

(1.CollegeofInformationScienceandEngineering，OceanUniversityofChina，Qingdao266100，China)

In this paper， which is based on the Jason-2 altimeter data， with the data of the significant wave height (SWH)， wind speed (U) and sea state bias (SSB) combination of 1-6 cycle in 12 different seasons in the cycle data as the training set， select the other 3 cycles of Jason-2 data as the test set. By the test analysis， the BP neural network model which corresponds to 3 cycles for estimating theSSBis established. The model is applied to the estimations ofSSBin the HY-2 altimeter， and the performances of the model can be evaluated by the goodness of fit betweenUandSWHbySSB， explained variance and residual contrast analysis. It suggests that the BP neutral network model can be effectively applied to the HY-2 estimations ofSSBand significantly better than the traditional parameter model of sea state bias．

radar altimeter; sea state bias; neural network model; wave height; wind speed

2016-09-05；

2016-12-05。

国家自然科学基金“雷达高度计海况偏差校正综合模型研究”(41176157)；国家自然科学青年基金“降雨条件下HY-2高度计有效波高反演技术研究”(41406197)；海洋环境安全保障重点专项“三维成像雷达高度计海洋信息提取技术及应用(2016YFC1401004)。

郭迎婷(1992—)，女，内蒙古自治区呼和浩特市人，主要从事海洋遥感方面研究。E-mail：2277134480@qq.com

*通信作者：苗洪利(1964—)，男，山东省青岛市人，教授，主要从事海洋遥感方面研究。E-mail：oumhl@ouc.edu.cn

10.3969/j.issn.0253-4193.2017.07.012

TP79

A

0253-4193(2017)07-0124-07

郭迎婷，苗洪利，张国首， 等. 雷达高度计海况偏差估计神经网络模型研究[J]. 海洋学报， 2017， 39(7): 124-130，

Guo Yingting， Miao Hongli， Zhang Guoshou， et al. Study on neural network model of estimating the sea state bias for radar altimeters[J]. Haiyang Xuebao， 2017， 39(7): 124-130， doi：10.3969/j.issn.0253-4193.2017.07.012