沿岸流非线性不稳定特征数值研究

沈良朵，邹志利，唐志波，倪云林，陈维

(1.浙江海洋大学 港航与交通运输工程学院， 浙江 舟山 316022;2.大连理工大学 海岸与近海工程国家重点实验室， 辽宁 大连 116024)



沿岸流非线性不稳定特征数值研究

沈良朵1，邹志利2，唐志波1，倪云林1，陈维1

(1.浙江海洋大学 港航与交通运输工程学院， 浙江 舟山 316022;2.大连理工大学 海岸与近海工程国家重点实验室， 辽宁 大连 116024)

当不稳定剪切波的波幅达到有限幅值之后，需要用非线性不稳定模型来分析沿岸流不稳定运动特征。本文通过建立并验证沿岸流非线性不稳定数学模型，在讨论该模型参数对沿岸流不稳定影响的基础上，率定实验中的模型参数并利用该数学模型模拟了实验中沿岸流不稳定的发展过程及其特征，主要结论有：(1)底摩擦系数越小，侧混系数越小，不稳定发生的时间越早，不稳定的波动幅值越大；(2)沿岸流非线性不稳定演化可能出现的5个阶段(线性阶段、倍周期阶段、大周期阶段、波群阶段以及不规则阶段)，实验中出现的沿岸流通常处于线性阶段或非线性倍周期阶段，倍周期阶段的涡旋是由线性阶段的涡旋发生追赶、配对直至合并产生的。涡旋配对以碰撞的形式发生，大部分能量转移至追踪波，然后以较慢的涡旋速度沿岸传播。

非线性不稳定；非线性；不稳定；沿岸流不稳定；沿岸流

1 引言

在波浪传向海岸过程中，除自身的周期性运动外，还有由于波浪非线性和波浪破碎而产生包括质量输移流、沿岸流、沿岸流不稳定运动及破波带内的旋涡运动等多种形式的水流运动。这些复杂的水流运动和波浪运动相互作用，会使海岸区域的物质输移扩散及泥沙运动出现复杂的运动形态。波浪的非线性使水质点的运动轨迹不封闭从而产生了质量输移流[1]；波浪斜向入射传至海岸时，为平衡辐射应力梯度，将沿岸波动动量转化为时均沿岸流动从而产生了波生沿岸流。随着对沿岸流认识的深入，近些年人们还发现沿岸流存在不稳定现象[2-3]，即沿岸流在沿岸流动的同时，速度矢量还存在长周期左右摆动。该沿岸流不稳定现象也被称为剪切波。Oltman-Shay等[2]通过观察发现了近岸破碎区周期O(1 000 s)、波长O(100 m)沿岸传播波动的存在。这些波动比观察到的对应频率的重力波波长要小得多。这些像波浪运动一样沿岸传播波动的存在及其属性与破波区沿岸流的存在、强度和方向有关。自Oltman-Shay等[2]在现场观测到的沿岸流不稳定运动以来，人们就对其特性进行了很多研究。Bowen和Holman[4]用线性不稳定理论解释了Oltman-Shay等[2]现场观测到的沿岸流不稳定现象，并将这种周期性低频振荡称为剪切波或者沿岸流不稳定运动。他们通过一个简单的流速剖面(其沿岸流离岸一侧的背景旋只有一个极值)阐述了剪切不稳定机理。但进一步研究发现线性不稳定理论只适用于小波幅的剪切波：a/L≪1，a和L分别为剪切波的波幅和波长。当不稳定剪切波的波幅达到有限幅值之后，需要用非线性不稳定模型来分析，因为随着沿岸流不稳定运动的进一步发展，由不稳定引起的扰动速度场、波面变化等使得原来线性不稳定模型中的一些假定不再成立，包括较小的扰动项和忽略掉的非线性项(非线性作用较强时，不能忽略)。

研究非线性波浪的一个有效方法是使用通过多尺度渐近展开得到的简单数学模型。同原始的浅水方程相比，这些模型一般应用范围有限，但只要潜在的假定是有效的，它们就能有效地描述非线性剪切波必要的动力特性。Dodd和Thornton[5]、Feddersen[6]利用弱非线性理论对海滩上的沿岸流不稳定进行了解析研究。结果表明：当沿岸流不稳定达到有限幅值后，就会改变平均沿岸流的分布。虽然弱非线性理论在超出线性区域的范围时对于理解不稳定运动的发展是有用的，但它仍局限于小波幅波浪的情况。对于浅水中所观察到的强非线性剪切波不再有效。Falques等[7]在“刚盖”假定的基础上建立了考虑底摩擦和侧混的非线性浅水模型，并在平面斜坡地形上用该模型进行了数值模拟实验。他们通过数值研究发现，非线性不稳定的波动幅值要么是周期性变化的，要么为常数；另外，他们还发现，非线性不稳定的波动周期随着波动幅值的增大而增大。Allen等[8]用数值模拟详细分析了平面斜坡地形下沿岸流不稳定运动受底摩擦系数和计算域在沿岸方向长度的影响。Özkan-Haller和Kirby[9]用考虑底摩擦和侧混影响的非线性浅水方程对SUPERDUCK实验中的沿岸流不稳定运动进行了数值研究。他们讨论了底摩擦与侧混效应对不稳定运动结果的影响，结果表明：底摩擦系数越小，则平均沿岸流越大，相应的速度波动幅值也越大，产生的涡旋运动也更剧烈；侧混系数越小，则速度时间历程波动幅值越大，不稳定运动波长越小，相应的涡旋运动也更加剧烈。Slinn等[10]用考虑底摩擦而没有考虑侧混的非线性浅水方程研究了两个沙坝地形上的剪切不稳定。他们发现底摩擦系数对不稳定运动波动幅值有较大影响：当底摩擦系数较大时，剪切波呈现等幅波动，与线性不稳定结果类似；当摩擦系数较小时，不稳定运动波动幅值逐渐变得不规则。Özkan-Haller和Li[11]通过辐射应力梯度项和波流相互作用项耦合研究了破波区沿岸流波流相互作用的剪切不稳定效应。Terrile等[12]利用相位重解模型(没有考虑波流之间的区别)求解了流场，研究了近岸环流中的涡旋输移运动。此外，任春平[13-14]利用最大熵谱估计分析了邹志利等[15]在大连理工大学实验室进行的沿岸流不稳定运动实验。Feddersen等[16]通过高阶Boussinesq模型数值模拟了加利福尼亚亨廷顿海滩附近波浪和沿岸流共同作用下HB06染料的扩散实验，模拟结果与破波区染料输移扩散现场实验观测到的低频涡旋吻合良好。以上提到的对沿岸流不稳定的研究中，当初始的平均沿岸流逐渐发展成有限幅值波动的沿岸流不稳定运动之后，所有研究者的思想都是基于Bowen和Holman[4]所用的线性不稳定理论。

2 沿岸流非线性不稳定控制方程

沿岸流不稳定水动力方程基于波浪周期平均和水深平均的二维近岸环流方程：

∂η∂t+∂∂x[ud]+∂∂y[vd]=0，

(1)

∂u∂t+u∂u∂x+v∂u∂y=-g∂η∂x+τx+τ′x-1ρdτbx，

(2)

∂u∂t+u∂u∂x+v∂u∂y=-g∂η∂y+τy+τ′x-1ρdτby，

(3)

式中，x和y分别为垂直海岸方向和沿岸方向，取x轴向岸为正，原点取在岸线上；η为波浪周期时间平均后的波面升高；h为静水水深，d=h+η为总水深；u和v分别为x和y方向的波浪平均和水深平均的水流速度；τx和τy为波浪驱动力；τ′x和τ′y为侧向混合项；τbx和τby为底摩擦力项。

把流动分为稳定的部分和波动的部分，则稳定情况下x方向和y方向的动量方程满足以下方程：

g∂η∂x=-1ρd∂Sxx∂x+∂Sxy∂y，

(4)

-1d∂∂xved∂V∂x+μdV=-1ρd∂Sxx∂x+∂Sxy∂y，

(5)

式中，Sxx、Sxy和Syy表示下标所指的相应方向的平均辐射应力。将波浪辐射应力分解为平均辐射应力和波动辐射应力之和，此时x方向的平均辐射应力由稳定的增减水η来表达，y方向的平均辐射应力可用稳定的速度剖面V来表达，这样表达的辐射应力满足下面的二维近岸环流方程：

∂η∂t+∂∂x[ud]+∂∂y[vd]=0，

(6)

∂u∂t+u∂u∂x+v∂u∂y=-g∂η∂x+g∂η∂x-

1ρd∂Sxx∂x+∂Sxy∂y+τ′x-1ρdτbx，

(7)

∂u∂t+u∂u∂x+v∂u∂y=-g∂η∂x-1d∂∂xved∂V∂x+

μdV-1ρd∂Sxy∂x+∂Syy∂y+τ′y-1ρdτby，

(8)

式中，Sxx、Sxy和Syy表示下标所表示相应方向的波动辐射应力，它们的值可这样求得：首先由初始入射边界处总的波能计算得到各位置随时间变化的波能，然后再减去各位置不随时间变化的平均波能，这样可以得到各位置随时间变化的波能的波动部分，由该波能的波动部分计算得到相应的波动辐射应力。对规则波而言，波动的辐射应力为0，故此时的波浪作用力项可简化为τx=g∂η/∂x和τy=-∂(νed∂V/∂x)/(d∂x)+μV/d。

方程中的侧向动量掺混作用力τ′x和τ′y，采用Özkan-Haller和Kirby[9]给出的公式计算：

τ′x=2d∂∂xνed∂u∂x+1d∂∂yνed∂v∂x，

τ′y=1d∂∂xνed∂v∂x,

(9)

式中，涡黏系数νe与能量损耗有关，可写由νe=Mhgh，系数M的范围为0.008～0.067。

方程中的底摩擦作用力项τbx和τby采用Haller耗散项[9]：

τbx=2μρuc，τby=μρvc,

(10)

式中，底摩擦系数μ=(2/π)fcwuwa，fcw为波流共存时的底摩擦系数，uwa为近底波浪水质点水平速度幅值。

需要指出的是方程中的波浪作用力包含辐射应力的波动影响，此时的能量方程应包含波能Ew随时间的变化项∂Ew/∂t，如式(11)所示。

∂Ew∂t+∂Ewcgcosα∂x=-S.

(11)

对于规则波来说，因为波能Ew不随时间的变化而变化，所以∂Ew/∂t=0。

3 模型验证

为了验证本文沿岸流不稳定运动模型的可靠性，本节针对Allen等[8]平面斜坡地形上的沿岸流不稳定运动进行了数值计算，因为本模型和Allen等[8]模型都采用二阶精度的中心差分和ABM格式的时间步进方法。通过计算所得的沿岸流不稳定运动时间历程和Allen等[8]的计算结果对比，发现结果差别很小，这表明本文所用的数学模型是可靠的。

计算区域的地形为平面斜坡，见图1，坡度为1∶20，垂直于岸方向的计算长度L(x)=1 000 m。初始流速V(x)采用n=3时的Allen型(V(x)=c0x2e-(x/α)n)平均沿岸流分布，并使其平均沿岸流最大值为Vmax=1 m/s，最大值位置距岸线x=90 m处。该流速剖面对应的沿岸流最大不稳定的增长率ωi相应的波数为k0=0.013 9 m，该波数对应的相速度cr=0.65 m/s。沿岸流不稳定运动的周期为2π/(k0cr)=690 s。本节计算的是沿岸方向的长度为1倍最不稳定增长率对应的波长λ0=2π/k0的情况，所以计算区域沿岸方向的长度L(y)=λ0=450 m。

图1 计算区域的海底地形Fig.1 Model geometry of the computational domain

图2给出了底摩擦系数μ=0.006时位于x=90 m,y=0.25L(y)=112.5 m处的垂直岸向速度u的时间历程Allen等[8]和本文数值计算结果的比较。

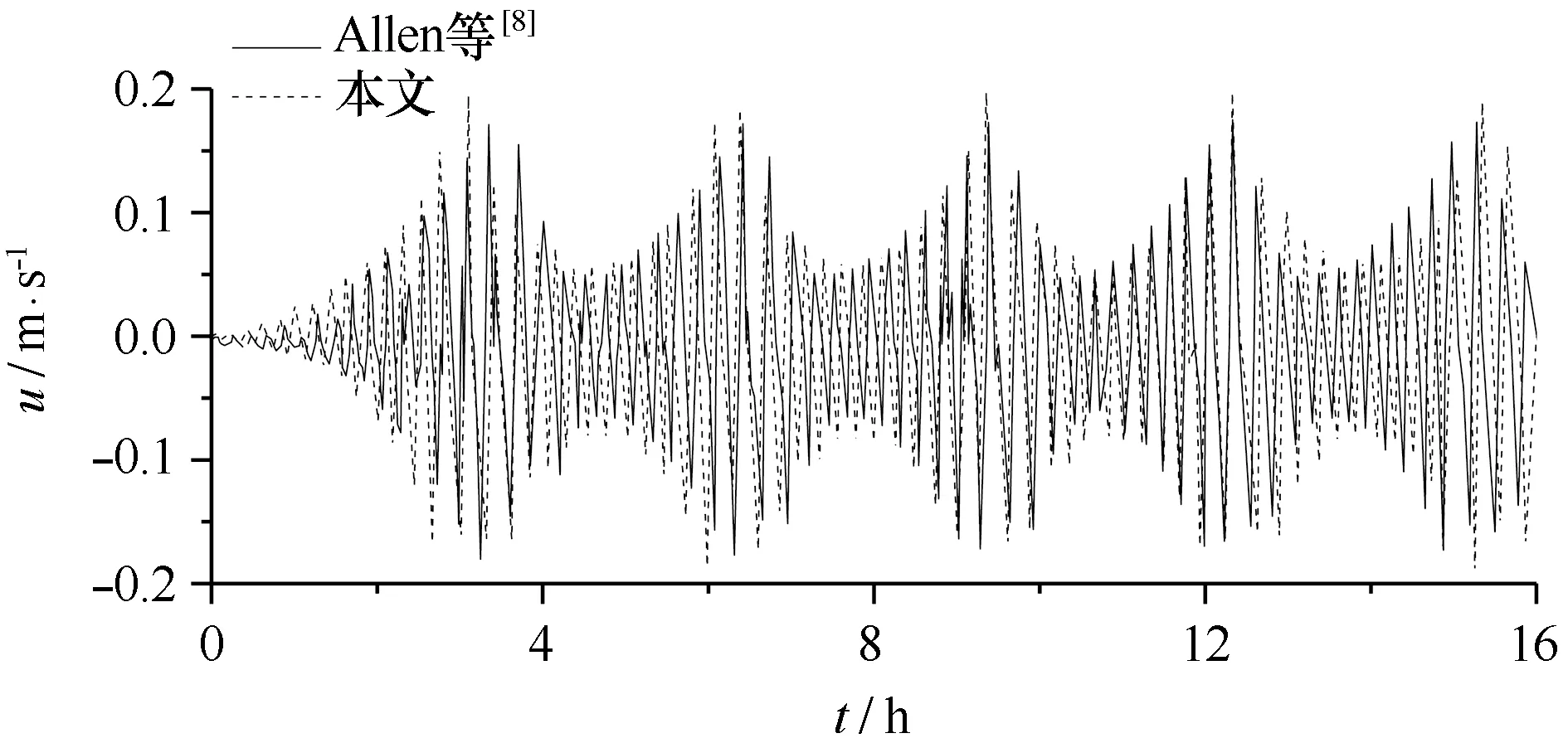
图2 Allen等[8]和本文垂直岸方向速度u的时间历程的比较Fig.2 Comparison of time series of u between Allen et al.[8] and this paper

由图2比较可知，本文的沿岸流不稳定运动模型能较好地重现Allen等[8]的数值计算结果。当μ=0.006时，本文的数值结果中速度u波动幅值出现了群的特征：群的周期约为3.2 h，每一个群周期含13个小周期波动，对应的每个小周期约为886 s，u的波动幅值的范围为0.06～0.20 m/s；Allen等[8]相应计算结果中速度的时间历程也出现了类似群的特征：群的周期约为3 h，比本文结果略小，每一个群周期含12个小周期波动，对应的每个小周期约为900 s，速度u的波动幅值为0.05～0.17 m/s，与本文的结果接近。需要指出的是空间步长对不稳定群周期有重要影响，当采用较大的空间步长时，相应的群周期也较大。通过与Allen等[8]结果的比较可知，每个不稳定波长大约需要200个网格点来确保模型的计算精度。

4 模型参数对沿岸流不稳定的影响

沿岸流不稳定非线性数学模型中包含底摩擦力项τbx和τby及侧向动量掺混作用力τ′x和τ′y项，Özkan-Haller和Kirby[9]在模拟SUPERDUCK现场实验中的剪切不稳定时指出，底摩擦与侧混对沿岸流不稳定计算结果有重要影响。这里以在大连理工大学所做的沿岸流不稳定实验波况(Tp=1 s，Hrms=5.63 cm)[17]为例(不考虑不规则波辐射应力的波动影响)，分别通过固定侧混系数M变换不同的底摩擦系数fcw来讨论底摩擦系数fcw对沿岸流不稳定的影响以及通过固定底摩擦系数系数fcw变换不同的侧混系数M来讨论底侧混系数M对沿岸流不稳定的影响。

图3给出了侧混系数M=0.02时，底摩擦系数fcw分别取0.000 25、0.000 5、0.001 5和0.005时，位于实验点(2.5 m，14.5 m)处垂直岸方向流速u和沿岸方向流速v的时间历程。由图3可见，在当底摩擦系数fcw取小于0.000 5时，流速时间历程出现了类似群的特性，随着时间继续，还会进一步发展成不规则波动的形式；增大底摩擦系数fcw至0.001 5时，群特性消失，经过一段时间慢慢发展成具有恒定幅值和倍周期的不稳定形式；再进一步增大底摩擦系数fcw时，流速时间历程波动消失，流速是稳定的。进一步比较发现，底摩擦系数fcw越小，不稳定越容易发生且不稳定出现得越早。

图3 不同底摩擦系数时流速u、v时间历程
Fig.3 Time series of velocities u， v for different bottom friction coefficients

图4给出了底摩擦系数fcw=0.000 5时，侧混系数分别取0.01、0.02和0.04，位于实验点(2.5 m，14.5 m)处流速u、v时间历程。由图4可见，和底摩擦系数fcw对沿岸流不稳定的影响类似，侧混系数M取较小值0.02时，流速时间历程出现了类似群的特性；减小侧混系数M至0.01，群特性消失，经过一段时间慢慢发展成具有恒定幅值和倍周期的不稳定形式；而当加大侧混系数M时，沿岸流不稳定则一直保持在等幅等周期的线性不稳定阶段。此外，侧混系数M越小，不稳定发生的时间越早，不稳定的波动幅值越大。

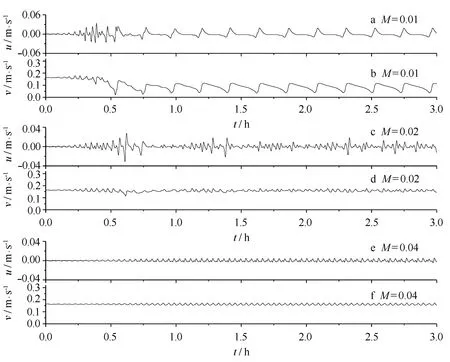
图4 不同侧混系数时流速u、v时间历程Fig.4 Time series of velocities u， v for different lateral mixing coefficients

表1 不同底摩擦系数和侧混系数作用下的不稳定特征

表1给出了上述不同底摩擦系数fcw和侧混系数M作用下的不稳定特征的汇总结果。进一步观察物理模型实验流速历程测量结果发现，底摩擦系数fcw取0.001，侧混系数M取0.02时，数值计算历程中0.38～0.58 h的波动特征和实验结果(低通滤波截断频率为0.1 Hz)吻合良好，见图5(数值计算时间由0.38～0.58 h平移至与实验记录相同的0～720 s)。实验中的波动周期约为200 s，而数值计算的约为164 s，与实验结果较为吻合；二者的波动幅值也较为吻合，约为2 cm/s。这表明底摩擦系数fcw取0.001时，能基本重现实验中出现的沿岸流不稳定现象，同时也表明该情况实验中沿岸流处于线性不稳定或弱非线不稳定阶段。

图5 流速u、v时间历程(┄)和实验结果(—)比较(实验点(x，y)=(2.5 m，14.5 m)Fig.5 Comparison of time series of velocities u， v at (x，y)=(2.5 m，14.5 m) between simulation and experimental result

5 实验中沿岸流非线性不稳定特征数值模拟

这里以物理模型实验不规则波况(Tp=2 s，Hrms=3.38 cm)[17]为例来说明沿岸流非线性不稳定的发展过程及特征。图6给出了该波况位于实验点距沿岸距离为14.5 m处垂直岸方向距离分别为1.0 m、2.0 m和3.5 m处流速u、v的时间历程，图7给出了对应位置处实验测量的流速时间历程的滤波线(滤波频率为0.1 Hz)。

由图6可见，该不稳定发展过程有一个相对稳定段(在t=0.38～0.51 h时间段)，对应的流速时间历程呈等幅等周期波动，此时对应的沿岸流处于线性不稳定发展阶段；经过该稳定段后，它会逐步发展成倍周期不稳定形式(不稳定波动周期约为396 s(t=0.68～0.90 h)，之后会进一步发展成大周期的波动形式。由图7可见，实验不稳定波动周期约为380 s，与非线性数值计算结果中倍周期阶段的波动周期接近，这表明该波况实验处于非线性发展的倍周期阶段，约为线性不稳定计算得到的波动周期(188.6 s[17])的2倍。此外，数值计算结果中沿岸流最大值位置处(x=2.0 m)的沿岸方向流速u的波动幅值约为2.0 cm/s，垂直岸方向流速v的波动幅值约为4.0 cm/s；而相应的实验结果沿岸方向流速u的波动幅值约为3.0 cm/s，垂直岸方向流速v的波动幅值约为4.5 cm/s，与数值计算的波动幅值接近。

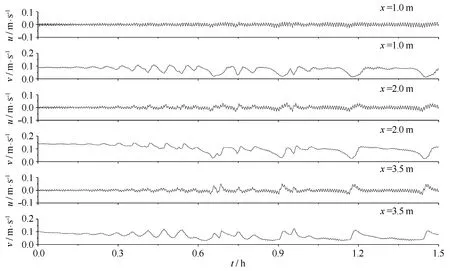
图6 数值计算流速u、v时间历程Fig.6 Time series of velocities u， v for simulation

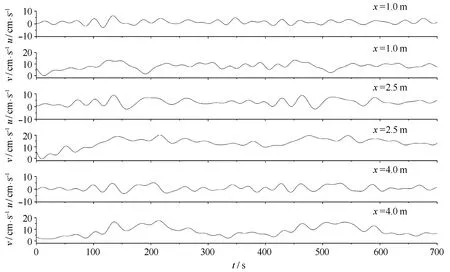
图7 实验测量流速u、v时间历程Fig.7 Time series of velocities u， v for experimental result

图8 涡旋及流场Fig.8 Contour plots of vorticity and velocity

图8给出了该波况不同时刻的涡量场和速度场。这些不同时刻的涡量场及相应的流场反映了涡的生成、发展及演化的过程。由图8可见，在t=1 440 s之前的沿岸流处于稳定状态，表现为负涡旋、正涡旋和零涡旋呈条形分布在近岸至离岸一侧。在这之后，开始生成一个规则涡并沿岸传播，表现为涡旋等间隔、等强度的沿岸均匀分布，这刚好对应流速时间历程的稳定段，产生的涡旋为规则涡，它们的相邻涡旋呈等强度、等距离分布并沿岸传播。此阶段的涡旋呈轻微向上隆起的条状分布，含一正一负两个涡旋，并没有形成非常明显的集中涡。相邻涡旋之间的距离约为20 m(由t=1 460 s的涡旋可看出，从沿岸5 m到20 m之间)；这与线性不稳定的波长计算结果(L=19 m)[17]接近。由相邻时刻涡旋的相对位置和间隔时间可知，该集中涡旋的传播速度约为0.04 m/s(经50 s，沿岸位置第一个涡旋由2 m传播至5.5 m附近)。随着不稳定的进一步发展，原来的规则涡开始发生变化，表现为相邻涡旋之间的距离发生变化，涡旋的形态也随之发生变化。在t=2 160 s时，在沿岸35 m附近出现了明显的较大的涡旋，相应的速度场也剧烈旋转；随着不稳定发展到后期阶段，涡旋之间会发生相互作用，生成一个更大的涡旋并沿岸传播。从涡量图来看，在t=4 320 s时，在沿岸方向均只包含一个大涡旋，呈大椭圆形结构，相应的速度场表明该区域内速度发生剧烈旋转。

结合第3节分析，沿岸流不稳定发展可能包含5个阶段，即线性阶段、倍周期阶段、大周期阶段、波群阶段和不规则阶段。

为了进一步阐述图8中涡旋发展演化过程，图9给出了该波况涡旋q(x0,y,t)位于x0=2.5 m处随时间演化的等值线图，其中红色区域代表正涡旋，蓝色区域代表负涡旋。图9a表示涡旋q(x0,y0,t)位于y0=7.5 m处的时间序列。这个沿岸y位置也用粗实线标记在等值线图上。涡旋波峰值沿-y方向传播，结果中涡旋的传播速度可由-dy/dt来表示，这表明直接从图上看时，斜率越大，则涡旋的传播速度越慢，反之斜率越小，则涡旋的传播速度越快。由图9可见，大约在t=0.8 h时，其中一个涡旋突然加速。图9a时间序列表明较快行进波的幅值比它前面波的幅值小。较快的涡旋最终赶上它前面的涡旋，在沿岸方向y=35 m处相碰撞。相应扰动将以较慢涡旋的速度传播。这种涡旋配对现象在图9中大约在t=0.9 h时再次出现，表现为斜率(-dy/dt)较小的涡旋(传播速度较快)以较快的传播速度赶上斜率(-dy/dt)较大的涡旋(传播速度较慢)，然后发生碰撞并合并，最终以斜率(-dy/dt)较大(传播速度较慢)的涡旋沿岸传播。这表明涡旋配对以碰撞的形式发生，大部分能量转移至追踪波，然后以较慢的涡旋速度沿岸传播。进一步观察图9发现，涡旋配对之后，将以恒定的速度和能量沿岸传播。涡旋配对后，涡旋大小q≈-0.1(1/s)，观察其中一个涡旋沿岸传播的过程发现，从t=1.12 h至t=1.39 h，涡旋传播的距离为37.95 m，计算可得涡旋配对后的传播速度约为0.040 m/s。

图9 随沿岸长度y和时间t变化的涡旋q等值线图(x0=2.5 m)，a图为涡旋在(y0=7.5 m)处的时间序列Fig.9 Contour plot of vorticity q(s-1) as a function of y and t at x0=2.5 m

6 结论

本文建立并验证了沿岸流非线性不稳定数学模型，讨论了模型参数(底摩擦和侧混系数)对沿岸流不稳定的影响，并利用该数学模型模拟了实验中沿岸流不稳定的发展过程及其特征，主要结论如下：

(1)沿岸流不稳定发展过程受数学模型参数的影响。底摩擦系数fcw越小，侧混系数M越小，不稳定发生的时间越早，不稳定的波动幅值越大。

(2)数值模拟了物理模型实验对应波况沿岸流非线性不稳定运动的特征。非线性不稳定演化可能出现5个阶段(线性阶段、倍周期阶段、大周期阶段、波群阶段以及不规则阶段)，实验中出现的沿岸流通常处于线性阶段或非线性倍周期阶段，倍周期阶段的涡旋是由线性阶段的涡旋发生追赶、配对直至合并产生的。涡旋配对以碰撞的形式发生，大部分能量转移至追踪波，然后以较慢的涡旋速度沿岸传播。

[1] Stokes G G. On the theory of oscillatory waves[J]. Trans Cambridge Philos Soc, 1847, 8(310):441-473.

[2] Oltman-Shay J， Howd P A， Birkemeier W. A. Shear instabilities of the mean longshore current 2. field observations[J]. Journal of Geophysical Research， 1989， 94(C12):18031-18042．

[3] Dodd N， Oltman-Shay J， Thornton E B. Shear instabilities in the longshore current: A comparison of observations and theory[J]. Journal Physics of Oceanography， 1992， 22：62-82．

[4] Bowen A J， Homman R A. Shear instabilities of the mean longshore current 1.Theory[J]. Journal of Geophysical Research，1989， 94(C12):18023-18030．

[5] Dodd N, Thornton E B. Longshore current instabilities: Growth to finite amplitude[C]// 23rd International Conference on Coastal Engineering,Venice, Italy,1992.

[6] Feddersen F. Weakly nonlinear finite amplitude shear waves[C]//Transactions of the American Geophysical Union Fall Meeting， San Francisco， California， 1996．

[7] Falqués A， Iranzo V. Numerical simulation of vorticity waves in the nearshore[J]. Journal of Geophysical Research， 1994， 99：825-841．

[8] Allen J S， Newberger P A， Holman R A. Nonlinear shear instabilities of alongshore currents on plane beaches[J]. Journal of Fluid Mechanics， 1996， 310：181-213.

[9] Özkan-Haller H T， Kirby J T. Nonlinear evolution of shear instabilities of the longshore current: A comparison of observations and computations[J]. Journal of Geophysical Research， 1999， 104：25953-25984．

[10] Slinn D N， Allen J S， Newberger P A. et al. Nonlinear shear instabilities of alongshore currents over barred beaches[J]. Journal of Geophysical Research， 1998， 103(C9):18357-18380．

[11] Özkan-Haller H T， Li Y. Effects of wave-current interaction on shear instabilities of longshore currents[J]. Journal of Geophysical Research: Oceans， 2003， 105(C5):3139．

[12] Terrile E， Brocchini M， Christensen K H， et al. Dispersive effects on wave-current interaction and vorticity transport in nearshore flows[J]. Physics of Fluids， 2008， 20(3): 481-1039．

[13] 任春平. 沿岸流不稳定运动的实验研究及理论分析[D]. 大连:大连理工大学， 2009．

Ren Chunping. A laboratory study and theoretical analysis on the instabilities of alongshore currents[D]. Dalian: Dalian University of Technology， 2009．

[14] Ren Chunping， Zou Zhili， Qiu Dahong. Experimental study of the instabilities of alongshore currents on plane beaches[J]. Coastal Engineering ，2011， 59(1):72-89．

[15] 邹志利， 任春平， 金红， 等. 沿岸流不稳定性运动实验研究[C]//第十二届中国海岸工程学术讨论会论文集. 北京:海洋出版社， 2005．

Zou Zhili， Ren Chunping， Jin Hong， et al. A laboratory study on the instabilities of alongshore currents[C]//The twelfth China Coastal Engineering Symposium. Beijing: China Ocean Press， 2005．

[16] Feddersen F， Clark D B， Guza R T. Modeling surf zone tracer plumes waves， mean currents and low-frequency[J]. Journal of Geophysical Research， 2011， 116(C11):11027．

[17] 沈良朵. 缓坡沿岸流不稳定性特征研究[D]. 大连:大连理工大学， 2015．

Shen Liangduo. Study of the feature of longshore current and its instability on mild beach slope[D]. Dalian: Dalian University of Technology， 2015．

Numerical study of nonlinear shear instability of longshore currents

Shen Liangduo1，Zou Zhili2，Tang Zhibo1，Ni Yunlin1，Chen Wei1

(1.SchoolofMaritimeandCivilEngineering，ZhejiangOceanUniversity，Zhoushan316022，China；2.StateKeyLaboratoryofCoastalandOffshoreEngineering，DalianUniversityofTechnology，Dalian116024，China)

It is necessary to analyze the characteristics of longshore current instability by using the nonlinear instability model when wave height reaches a finite amplitude. Building and verifying the nonlinear instability mathematical model of longshore current， this paper discusses the influences of model parameters and obtains the value of model parameters corresponding to the experimental result. The development process and its characteristics of longshore current instability in experiment are simulated and illustrated by the mathematical model. Key innovations include: (1) the smaller the bottom friction coefficient and lateral mixing coefficient， the sooner the instability occurrence， the bigger the fluctuation amplitude is; (2) the evolution processes of longshore current include five stages (linear， double period， larger period， wave group and irregular stages). The longshore current instability in the experiment occurs in stages of linear or double period. The vortex in double period stage forms by the vortexes in the linear stage which catch， match and merge one another. The match of vortex occurs in collision， the major energy transfers to trace wave and spreads along the coast at a slower rate of vortex．

nonlinear shear instability; nonlinear; instability; longshore current instability; longshore current

2016-08-17；

2017-02-05。

浙江海洋大学创新团队基金，科研启动经费资助(11185010817)；国家自然科学基金(10672034)。

沈良朵(1982—)，男，安徽省安庆市人，博士，讲师，主要从事近岸水动力方面研究。E-mail：slduo@163.com

10.3969/j.issn.0253-4193.2017.07.003

P731.2

A

0253-4193(2017)07-0026-10

沈良朵，邹志利，唐志波， 等. 沿岸流非线性不稳定特征数值研究[J]. 海洋学报， 2017， 39(7): 26-35，

Shen Liangduo， Zou Zhili， Tang Zhibo， et al. Numerical study of nonlinear shear instability of longshore currents[J]. Haiyang Xuebao， 2017， 39(7): 26-35， doi：10.3969/j.issn.0253-4193.2017.07.003