波浪-海流-微地形耦合的沉积动力模式建立及应用
2017-07-07芦静夏长水滕涌刘学海
芦静,夏长水,滕涌,刘学海
(1.中国海洋大学 海洋与大气学院,山东 青岛 266100;2.国家海洋局第一海洋研究所 海洋环境科学和数值模拟国家海洋局重点实验室,山东 青岛 266061)
波浪-海流-微地形耦合的沉积动力模式建立及应用
芦静1,2,夏长水2,滕涌2,刘学海2
(1.中国海洋大学 海洋与大气学院,山东 青岛 266100;2.国家海洋局第一海洋研究所 海洋环境科学和数值模拟国家海洋局重点实验室,山东 青岛 266061)
沙纹微地形普遍存在于海底,沙纹的消长能改变底部应力进而影响泥沙的运移。以往研究较多侧重于波致沙纹,并已应用于波浪模式的底摩擦计算,而较少考虑波流联合效应产生的沙纹,也未将其应用于综合的水动力模式和沉积物输运模式。本文在POM水动力模式中嵌入新南威尔士大学泥沙模式,通过耦合波流共同作用的微地形模型与波流相互作用底边界层模型,发展了波浪-海流-微地形(沙纹)耦合的沉积动力模式。本文将该模式应用于澳大利亚Jervis湾,针对波主导和波流联合主导沙纹两种类型,分别进行了沙纹发展状态、几何形态的分布及悬浮泥沙的模拟。结果表明:波致沙纹比波流联合作用的沙波具有更大的波高和波长,因此当波主导时沙纹对悬浮泥沙起着关键作用。通过考虑随沙纹变化的粗糙度,相比于以往模式设置均一的粗糙度,该模型能对悬浮物浓度的骤升过程进行更精细的预测。
沉积动力模式;波流耦合;微地形;沙纹;底边界层;底粗糙度;悬浮泥沙
1 引言
沙纹微地形为在沉积层表面形成的类似于水波纹的微细形态,其波长通常在几厘米到几十厘米。沙纹普遍存在于近岸非黏性底质的海底,偶尔也会在黏性底质出现。底应力作用是沙纹变化的主要动力因素,底应力的产生主要为波浪和底层流两部分。按照沙纹主导机制,可分为波主导沙纹、流主导沙纹和波流联合主导沙纹。
沙纹微地形可增加海底湍动能,因此对泥沙输运具有重要的意义。沙纹出现能显著增大底粗糙度,底部应力又是水动力和海底粗糙度共同作用的结果,因此沙纹的存在可使底部应力骤升,而底应力是决定底边界层中泥沙再悬浮和沉积的关键。当海底为平底时,粗糙度由海底沉积物的粒度特征决定。一旦沙纹产生,将使底粗糙度显著增大。Babanin等[1]对澳大利亚Lake George粉砂的实验室研究表明沙纹的出现可使Nikuradse粗糙度Kb增大60倍。可动沙纹底形发展过程本身属于推移质运动的一种形式,但它同时又影响悬移质运动。由于推移质输沙量与沙纹运移速率和沙纹的波高成正比,沙纹可作为推移质运动的指征用来评估推移质运移的方向和大小[2]。悬浮泥沙运移受底部混合的影响极大,沙纹可以通过扩散和对流涡旋过程影响悬浮泥沙的夹带机制,其计算依赖于不同形态函数类型以及参考浓度[3—5]。
波浪和海流均能产生沙纹,但一直以来波浪主导的沙纹得到研究重视[1,6-8],而海流主导的沙纹研究较少。波、流联合主导沙纹则限于复杂的相互作用机制,相关的研究更是少之又少,但在综合的水动力模型中只考虑波浪产生的沙纹是不足的。Li和Amos[9-10]将沙纹引入一维沉积物输运模型中,提出一个计算波流共同作用下的沙纹的算法,但其对沙纹增强的剪切速度的计算尚不完善。
虽然沙纹的存在非常普遍,但以往很少将其影响引入到沉积动力模式中,其对悬沙及推移质运移影响的研究更少。Tolman[11]给出了沙纹引起的波浪耗散的参数化方案并引入到WAVEWATCH波浪模式中, Ardhuin等[12]对该方案进行了修正。Smith等[8]将波致沙纹引起的底摩擦引入SWAN模式,提高了近岸的波浪模拟精度。在当前的沉积模式中,往往采用均一的海底粗糙度设置,既不能体现物理要素在空间上的细微分布,也不能体现微地形随时间的变化,从而影响了对底层和近底层的动力机制及各物理要素分布变化的精细模拟。
本文发展了建立波浪-海流-微地形耦合的沉积动力模式,该模式通过改进参数化方案,建立模拟波流联合作用下的沙纹几何形态的模型,并实现沙纹模型与波流相互作用底边界层模型[13-15]的耦合。首先,我们参考并改进了Li和Amos[9-10]及Tolman[11]的参数化方案,并编写了独立模块来模拟波流联合作用下的沙纹几何形态;第二,改进沙纹增强的剪切速度计算模型,考虑沙纹的时空变化及其对底层剪切速度的影响,代替通常使用的均一粗糙度设置;第三,体现沙纹对悬浮泥沙浓度的作用,建立的模式将能够更精细的模拟悬沙运移状况。本文还将该模式用于Jervis湾悬浮泥沙的模拟,给出该海域沙纹的几何形态分布及沙纹影响下悬沙浓度随底层流及波浪的演变规律。
2 耦合模式的建立
2.1 沉积物输运模式
我们以普林斯顿大学海洋模式(POM)[16]作为水动力基础,并将新南威尔士大学泥沙模式(UNSW-Sed)嵌入到POM模式中。UNSW-Sed由POMSED发展而来[17-19],它具有以下特点:第一,通过引入通量Richardson数Rf,考虑了底边界层化效应[17]。拖曳系数Cd为:
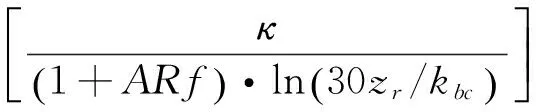
(1)
式中,A=5.5,是经验常数;zr是参考高度;kbc是表观粗糙度,它由波浪边界层和底物理粗糙度联合得到;κ是卡曼常数;Rf为通量Richardson数。根据Blumbery和Mellor[20],通量Richardson数Rf可由二阶湍封闭算法中的梯度Richardson数Ri计算:
Rf=0.725[Ri+0.186-(Ri2-
0.316Ri+0.034 6)1/2],
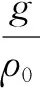
(2)
第二,根据雾状层动力学,考虑了悬浮泥沙对海水密度的贡献及泥沙密度对水动力的影响,适于模拟异重流等情况。本文在UNSW-SED基础上做了如下两点改进:一是将微地形模型嵌入波流相互作用的底边界层模型[13-15],并考虑了波致底沙液化[21]对底床的侵蚀作用;二是改进了悬浮泥沙浓度辐射边界条件。
2.2 波流共同作用的底边界层模型
2.2.1 波流联合作用下的最大底切应力
基于波流耦合的底边界层模型[13-15],波流共同作用下的最大底切应力可表示为:
(3)
式中,τc为流致底切应力,它是一个平均分量;τw为波致底切应力,它是扰动分量的最大值。不考虑平均应力分量τc对扰动分量τw的作用。u*cw为波流共同作用的剪切速度,波流共同作用下的底切应力τb是决定沉积物在底边界层中再悬浮和沉积通量的关键因子。
2.2.2 波浪边界层和底物理粗糙度联合引起的表观底粗糙度
采用Signell等[15]的方法引入波浪对底流速的作用,根据波浪摩擦/剪切速度u*w利用迭代过程来确定参考高度zr处的粗糙度。底边界模型中,定义波浪边界层和表观粗糙度kb联合引起的Nikuradse底粗糙度kbc,
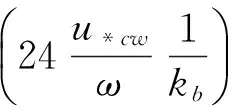
(4)

2.3 沙纹微地形计算模型
将上文的波流耦合底边界层模型和微地形模型结合起来,以考虑沙纹存在产生的底边界效应。
2.3.1 波/流主导的沙纹类型
要计算沙纹的几何形态,首先须判断沙纹的主导类型。波浪剪切速度与稳定流的剪切速度之比U*ws/U*cs可用来定义波流共同作用下不同种类的沙纹:当U*ws/U*cs<0.75时流主导;当U*ws/U*cs>1.25时,波浪起主导作用;当0.75 2.3.2 波流联合作用下的沙纹发展状态 沙纹的5个发展阶段[9-10]由剪切速度与不同临界值的比较界定:(1)无传输状态,U*cwe 表1 主要变量的定义 由于沙纹仅为几厘米到几十厘米量级,在数值计算中通常难以直接分辨其形态,因此粗糙沙纹底床上的底摩擦通常难以模拟。本文采用参数化方案,以沙纹的波高和波长为描述沙纹几何形态两个指标,模拟它们随时间和空间的变化。参数化方案参考Li和Amos[9-10]的实验室和现场观测,我们将该方案与波流耦合沉积动力学模型衔接,并进行了对计算沙纹增强的剪切速度做了改进(见2.3.4节)。 沙纹波高和波长的计算公式如下: (1)无传输状态,U*cws (2)弱传输状态,U*cws η=(19.6·U*cws/U*cr+20.9)D,λ=η/0.12, (5) 式中,D为底沙的中值粒径。 (3)平衡状态,U*cws≥U*cr且U*cwb a.当波主导,即当U*ws/U*cs≥1.25时, η=27.14·U*cws/U*cr+16.36D,λ=η/0.12, (6) b.当波流联合主导,即当U*ws/U*cs<1.25时, η=(22.15·U*cws/U*cr+6.38)D,λ=η/0.15. (7) (4)破碎状态,U*cwb≥U*bf时, λ=535D,η/λ=0.15U*up-U*cwb/ U*up-U*bf. (8) (5)层移状态,U*cwb≥U*up时,理论上无沙纹。此时模式中仍然设置最小值η=0.01 m,λ=0.1 m,因此沙纹波陡η/λ=0.1。 2.3.3 沙纹增强的底粗糙度 Nikuradse粗糙度Kb由下式计算: Kb=27.7η2/λr+170D(θs-0.05)0.5+2.5D. (9) Kb分为3部分:(1)底沙粒径产生的粗糙度为2.5D,D为底沙中值粒径;(2)170D(θs-0.05)0.5为推移质运动引起的粗糙度;(3)沙纹产生的粗糙度为27.7η2/λr。θs为Sheilds参数,由波流联合作用下的底切应力决定。 2.3.4 沙纹增强的剪切速度及其改进 以往常用Nielsen[22]的结果计算沙纹增强的剪切速度U*cwe,但其仅基于粒径的剪切速度U*cws和沙纹波陡,并只是简单线性关系的表达式U*cwe_NL=U*cws/(1-πη/λ),而U*cws由不考虑沙纹的且均一的Kb计算得到。而本文采用改进的沙纹增强的波流联合剪切速度U*cwe_Kb,它由沙纹增强的Nikuradse粗糙度Kb(公式(9))导出。 我们改进的沙纹增强剪切速度U*cwe_Kb所使的沙纹增强粗糙度经波浪修正得到。通过考虑波流相互作用修正粗糙度Kb(波)以获得Kbc(流),Kb和Kbc用于计算波致底切应力的波浪摩擦因子fw及拖曳系数Cd,然后分别计算出流致剪切速度U*c和波致剪切速度U*w,再由公式(3)叠加得到U*cwe_Kb。也就是说,一方面,我们通过Kb引入了沙纹的效应,而在另一方面,我们通过修正Kb(沙纹增强的粗糙度)来引入表面波的效应。因此,这种方法比使用Nielsen[22]的表达式更加符合物理过程。 3.1 模式区域地理位置、概况及网格分布 Jervis湾位于澳大利亚东南海岸、新南威尔士州南部,面积136 km2,是一个半封闭港[23]。Jervis湾南部陆地岬角设有海军基地。Jervis湾的平均深度为15 m,北半部的浅水陆架广阔,通过宽3.75 km的湾口与外陆架相连。湾内潮流较弱且主要由M2分潮控制[23]。湾口潮流流速约为0.07 m/s,而在湾北部潮流流速则小于0.01 m/s[24]。 Jervis湾沉积物以粗沉积物(CSM)为主,CSM的平均含量约占77%;但在Jervis湾北部的沉积物中,细颗粒泥沙物质(FSM,粒径介于2~20 μm之间)的组分含量较高(达47%)。在Jervis湾也可以观测到最细的黏土和淤泥沉积物(小于2 μm),但细颗粒泥沙在Jervis湾中并不占主导地位(组分含量小于7%)[25]。 模式区域为31.45°~37.95°S,150.0°~156.95°E(图1b)。网格设置为正交曲线网格系统,并在Jervis湾局部加密(图1b),网格数为234×258。x方向的水平分辨率为438~7 403 m,y方向的水平分辨率为556~6 922 m。垂向分为21个均匀的sigma层。 3.2 边界条件 关于潮汐边界的设置,我们考虑了4个主要分潮,即M2、S2、K1和O1。风场强迫和外部波浪边界条件由ECMWF(Centre for Medium-Range Weather Forecasts)全球模式获得。我们使用的ECMWF数据的分辨率为0.125°×0.125°,时间间隔为6 h。SWAN模式用10 m风速的U和V分量来驱动。ECMWF波浪资料被应用在3个开边界上,这些开边界条件由波浪和涌浪叠加的有效波高、平均波周期和平均波向组成。 3.3 泥沙参数及沙纹临界值的选取 表2给出了泥沙输运模式中系数的选取。根据澳大利亚地球科学院于2007、2008和2009年的调查结果,粒径覆盖范围200~400 μm。在本文最关注的E站和F站,砂质组分所占比例超过85%,E站附近的平均粒径大约介于300~350 μm之间,而F站附近的粒径大于300 μm。因此,本文设置粒径D为中间值340 μm,以确保应用Li和Amos[9-10]的方法和参数的合理性,他们的方法基于实验室观测和现场测量,也设置了0.34这个粒径值。根据Miller等[26]的Yalin方法用来获得临界Shields参数θcr, 然后由此得出推移质运动的临界剪切速度U*cr。悬移质启动的临界应力τcrs由Bagnold[27]得出。Jervis湾主要为非黏性底质,根据Gibbs等[28]的表达式,使用中值粒径计算的沉降速度Ws具有10-3m/s的量级。动力学黏性系数μ的变化范围根据不同水温等条件变化范围为0.001~0.001 2 N·s/m2。层移(推移质运动的最高级别)临界Shields参数θ*up根据Li和Amos[29]的一个通用化的标准导出。 图1 模型区和网格系统 表2 泥沙模块中的主要参数 3.4 数值实验设置 我们进行了不同的数值实验(表3),包括考虑或不考虑沙纹的比较,并比较了使用U*cwe_Kb或U*cwe_NL之间的沙纹状态及沙纹引起的悬浮泥沙浓度(suspended sediment concentration,SSC)差异。对于没有沙纹的实验,Kb设定为均一的0.05 m,这相当于有或者没有沙纹的平均值。 表3 沙纹数值实验 3.5 观测仪器布放及数据分析方法 水位的观测在Tg站(图1a)使用Manly液压实验室(MHL)开发的电磁测潮仪(EG),间隔15 min采集水位数据。有效波高的验证选择了的分别位于Batemans湾和悉尼外海两个波浪骑士浮标。浮标施放地点位置见图1b由白色菱形标注。Batemans湾和悉尼外海浮标观测点的水深分别是55.7 m和93.9 m。波浪骑士浮标适于在较深或中等水深处投放,浮标施放位置的水深及邻近条件可以使得波浪折射、衍射及浅水效应和摩擦衰减的影响微小而忽略。我们在Jervis湾布放了ADP实施高频流速的测量,坐底式ADP每小时观测1次,每次持续流速采样时间间隔为1 s。布放于2009年11月16日在E站(35.113°S,150.708°E,水深11 m)进行,并回收于2009年12月18日。E站位于Jervis湾西南,站点E的位置见图1a白色圆圈。 由信噪比(SNR)分析获得SSC作为一种替代性的测量已被广泛应用[30-31]。校准方程通常遵循一种对数的形式。在本文中,我们使用Xavier等[31]的表达式,实验室结果显示相关系数达0.99。 4.1 水动力模式验证 4.1.1 大风过程中的浮标观测的有效波高验证 强风过程可以用来检验测试模型预测风浪的能力,因此我们选择一个风速大于10 m/s的时间段用来验证波浪模式,涵盖从澳大利亚东部标准时间2009年10月10日10:00之后的457 h(图2)。图2表示风速大于10 m/s的条件下,在Batemans湾和悉尼外海的有效波高浮标观测与模拟的比较。 图2 2009年10月Batemans湾(a)和悉尼外海(b)近岸有效波高浮标观测与模拟比较Fig.2 Validation rom offshore buoys in October 2009 in Batemans Bay (a) and Sydney (b) 图2的波浪模拟结果显示,在波浪近岸复杂因素可以忽略的情况下,SWAN模拟结果与实测符合较好,且与风速的发展趋向及数量变化基本符合。在此大风过程中,有效波高的决定因素基本来自本地风场。 4.1.2 水位的验证 图3给出了Jervis湾西南Tg站2008年和2011年两次水位模拟结果与基于电磁验潮计的资料的对比。 我们使用了潮汐站Tg(图1a)的水位来验证模式的各分潮(图3)。模式与观测结果的均方根(RMS)误差计算公式如下: (10) 式中,A和φ分别是潮汐振幅和位相;下标m和o分别表示模拟和观测。表4给出了2008年和2011年用于模型强迫的4个主要分潮的观测和模拟的结果的均方根误差统计。 表4 2008年和2011年各分潮观测和模拟结果之间的均方根误差对比 图3 2008年(a)和2011年(b)Tg站的观测和模型潮位对比Fig.3 Comparison of tidal level from observation and model results at the Site Tg for 2008 (a) and 2011 (b) 图4 模拟的2009年11月Jervis湾局部沙纹类型(a)和发展阶段(b)Fig.4 Distributions of ripple types, ranges and geometry with Jervis Bay locally amplifieda.流/波主导类型:色标值-1代表当U*ws/U*cs<0.75时流主导, 1代表当U*ws/U*cs>1.25时波主导, 0代表当0.75 从图3及表4来看,模式计算的各分潮振幅和相位的时间序列及误差均达到使用要求。 4.2 沙纹的水平分布 4.2.1 沙纹的波流主导类型以及发展阶段 不同的海底动力条件下的沙纹形态各异。波致海底表面摩擦(剪切)速度与稳定流产生的摩擦(剪切)速度的比值,U*ws/U*cs被用来计算波流联合流作用下的沙纹类型(浪/流主导)(2.3.1节)。图4和图5的平均分布,是指本文模拟的2009年11月期间的平均状态,这期间涵盖波浪增大和减小的状态。我们将11月每小时的输出结果进行月平均。 图4给出了模式模拟的Jervis湾内各种沙纹的分布及变化。针对沙纹类型,模式输出-1代表流主导,输出0代表波流共同主导,输出1代表波主导。平均得到的值就会位于-1到1这个区间上,由此得到图4a。平均值越接近1,波浪的成分就越大,越接近-1,流的成分就越大。针对沙纹发展阶段,模式输出0代表无传输阶段,模式输出1代表弱传输阶段,模式输出2代表平衡状态,模式输出3代表破碎状态,模式输出4代表层移状态。平均值位于0到4这个区间上,由此得到图4b。平均值由0增加到4的过程中,水动力作用逐渐增强,沙纹开始出现,波高波长由小变大,最后沙纹发生破碎,沙纹消失。 由图4a可见,波浪在水深小于10 m的近岸海区起主导作用(U*ws/U*cs>1.25),而流主导(U*ws/U*cs<0.75)的区域在Jervis湾中部水深大于20 m的海区,波流联合主导0.75 4.2.2 模拟沙纹几何形态 图5a和5b分别为11月每小时的输出的沙纹波高和波长的月平均。图5给出了模拟的Jervis湾内沙纹几何形态(即平均波高和波长)的水平分布及变化。 图5 模拟的Jervis湾局部沙纹几何形态的平均分布Fig.5 Averaged distributions of ripple geometry with Jervis Bay locally amplified 图5a和5b显示出沙纹波高和波长的分布及大小与图4a和4b中的沙纹类型和状态有相似的分布趋势。沙纹波高η(10~14 cm)和波长λ(9~12 cm)通常在波主导的区域较高;此外,湾口也呈现出较大的沙纹波高和波长,其原因可能是潮流较大。这意味着,波浪主导的沙纹的波高和波长通常高于流主导的沙纹波高和波长。在Jervis湾外侧东北部的近岸区域,沙纹从破碎状态发展到层移状态,沙纹波高和波长在平衡状态达到最高,从破碎状态发展到层移状态的过程中逐渐减小。 4.3 沙纹随底层流及波浪的演变规律 4.3.1 悬沙浓度验证以及沙纹对其作用 E站位于东南沿岸的外海11.0 m水深处,ADP于2009年11月在此布放。E站大多数时候的沙纹类型为波浪主导(图4a和图7b)。F站选在湾口的东北处,这里的潮流较强。因此F站具有典型的流主导的沙纹特征(图4a和图8b)。F站没有ADP流观测,选取F站的原因是为了确定我们在波占主导地位的区域得出的结论是否只适用于波主导的沙纹还是同样适用于流占主导的沙纹区域。 图6显示了2009年11月E站和F站处沙纹相关的各项模拟结果。如图6所示,考虑沙纹的SSC变化更为剧烈与也与观测符合更好。从图6a和6b来看,考虑沙纹的SSC都比不考虑沙纹时变化更为剧烈。考虑沙纹的情况下,底切应力(bottom shear stress, BSS)能达到5.0 N/cm2,SSC达到60 mg/L,而在无沙纹(设置平均Kb=0.05 m)的实验中,模拟的最大BSS仅为2.0 N/cm2,SSC为20 mg/L。然而,在BSS低于0.8 N/cm2的部分,考虑沙纹情况下BSS和SSC低于不考虑沙纹情况。 图6 2009年11月26日00:00至28日17:00 E站(a)和F站(b)的SSC以及E站(c)和F站(d)的底层流速和波轨道速度,其中E站有ADP观测Fig.6 a and b are SSC from 00:00 on 26th to 17:00 on 28th November, 2009, c and d are bottom tidal velocity and wave orbital velocity, a and c are for Site E with ADP measurements 图7 E站(a)和F站(b)分别使用U*cwe_Kb和U*cwe_NL计算的沙纹状态时间序列Fig.7 Time series of ripple stages at Site E (a) and Site F (b) under U*cwe_Kb and U*cwe_NL respectively最上方框为波主导,中间灰色方框代表波流联合主导,最下层方框为主导;3种不同波或流主导的状态下又分别包括无传输状态、弱传输状态、平衡状态、沙纹的破碎状态和层移状态The top box represents wave dominant, the middle box represents combined flow dominant, the bottom box represent current dominant. These 3 wave/current-dominant stages include no transport ranges, weak transport ranges, equilibrium ranges, break off ranges and sheet flow statuses 图8 E站(a)和F站(b)沙纹几何形态的时间序列及使用U*cwe_Kb和U*cwe_NL的比较,虚线中间灰色区域与ADP观测时间对应Fig.8 Time series at Site E(a)and Site F(b)ripple dimensions and their comparison between using U*cwe_Kb and U*cwe_NL,time period between dashed lines corresponds to measurement time 图9 2009年11月E站(a,c)和F站(b,d)拖曳系数Cd(a,b)和波浪摩擦因子fw(c,d)时间序列Fig.9 Time series of drag coefficient Cd(a,b)and fw(c,d) in November 2009 at Site E(a,c) and Site F(b,d) 在波通常占主导地位E站(图4a),使用U*cwe_NL计算的SSC与观测相比明显被低估了。波浪在近岸区域起着关键作用,因此该低估不能忽视。再悬浮的临界底切应力为1.2 N/m2(剪切速度0.034 9 m/s),推移质运动的临界剪切应力为0.16 N/m2(剪切速度0.012 7 m/s) (表2)。如果我们人为设置再悬浮的临界剪切应力,给定一个较低值,如0.50 N/m2, 使用U*cwe_NL时SSC的峰值也有会被模拟出来,然而0.50 N/m2(相当于剪切速度0.022 m/s)远小于之前Li和Amos[9-10]的临界值标准(1.2 N/m2),这个临界值针对0.34 mm粒径由Shields参数计算得到。对于波浪并不主导的F站,使用U*cwe_Kb或者U*cwe_NL模拟的BSS在波浪较大时仍然呈现出较大的差异。 4.3.2 沙纹发展状态及几何形态的演变规律 图7给出了E站和F站不同类型沙纹(波/流主导)的发展状态。由图7可见,U*cwe_Kb和U*cwe_NL之间的差异主要出现在从“无传输状态”到“弱传输状态”的过渡过程。当考虑沙纹时,低估U*cwe导致了底床停留在无传输状态,而不是进展到弱传输状态。同时,图7c也说明E站沙纹是主要由波主导的。平衡态沙纹相对出现较少,E站以无传输和弱传输状态为主。 F站属于波流联合主导的海区(图4a)。F站接近Jervis湾湾口,这里潮流流速是E站流速的2倍。在波浪较小时,F站的沙纹类型可以达到流主导的无传输状态(图7b)以及波流联合占主导的弱传输状态。 图8给出了E站和F站沙纹几何形态的时间序列。如图8所示,流或波流联合主导的沙纹(图8b)比波浪主导的沙纹(图8a)在沙纹波高η和波长λ的变化上更加平缓。沙纹波高和波长在沙纹产生后迅速上升,到达顶峰后逐渐减少。沙纹波高变化范围为1~2 cm,而沙纹波长变化范围为8~13 cm。沙纹波高η和波长λ都在平衡状态达到最大值。使用U*cwe_Kb或U*cwe_NL,沙纹几何形态(波高和波长)并未出现明显变化。究其原因,U*cwe仅仅是用以通过和临界值比较,决定底边界状态是否从无传输升级到弱传输状态;而U*cws和U*cwb则通过和临界值比较来判断沙纹处于平衡、破碎还是层移状态。 如图9所示,使用Nielson(1986)方法计算的拖曳系数Cd_NL略大于使用我们Kb方法计算的Cd_Kb。拖曳系数Cd经过波浪修正后得到Cd_new。然而,在波浪存在时,fw_Kb明显高于fw_NL。因此fw是造成U*cwe_Kb甚至比U*cwe_NL大的关键。U*cwe_Kb与U*cwe_NL的差别主要体现在波致剪切速度U*w上。 5.1 随沙纹变化的粗糙度 粗糙度是影响的底切应力BSS和SSC的关键因素。当不考虑沙纹时,以前的模式往往假设了均一的Nikurade粗糙度Kb或者Z0(Kb/30)。例如,在POM模式的水动力模拟中Z0被设置为0.01 m,以及在Ecomsed泥沙模式中Z0被设置为0.001 4 m作为默认值。这个默认的Kb通常是一个平均状态,这个平均态比仅仅基于粒径的Kb(gs)高,但往往比沙纹增强的Kb(gs+bl+rp)小。导致的结果是,平均的Kb不能体现沙纹发展的动态过程,因而不能更好地模拟SSC的变化。 5.2 波浪效应的数值稳定性 5.3 平均或最大波浪轨道速度的选取 当考虑波浪效应对粗糙度的影响时,我们使用平均波浪轨道速度。因为当用波浪修正表粗糙度Kb而得到表观粗糙度Kbc(Kbc为计算拖曳系数Cd所需),是波浪的平均状态影响波浪在波流共同作用中所占的比例(公式(4),系数β)而不是最大状态。类似地, Smith等[8]通过积分波浪谱来获得平均近底轨道速度Ub并用于计算波致沙纹。 然而,当确定底部泥沙是否会发生再悬浮时我们使用波浪轨道速度最大值来计算波致底切应力,因为是波浪扰动分量的最大值决定了底沙是否能够进入水体[14]。这时,流致底切应力为平均量,而不是一个周期性变化的值。因此波流共同作用下的最大底切应力τb,max(公式(3))是平均流致切应力与最大的波浪致切应力的叠加。 6.1 沙纹微地形对悬浮泥沙的影响 当沙纹出现时,波浪可以大幅提高悬浮泥沙浓度SSC。考虑沙纹之后,SSC比不考虑沙纹时变化更为剧烈。因此,与以往采用均一的底粗糙度相比,考虑沙纹之后实际观测的SSC骤升过程被更准确地模拟出来。此外,我们改进了计算沙纹增强的剪切速度的方案,记为U*cwe_Kb,当波浪主导时,使用我们提出的剪切速度U*cwe_Kb可明显提高SSC的模拟量值,与观测也更为符合。在无传输和弱传输状态,使用U*cwe_NL与U*cwe_Kb,造成的SSC差异也不甚明显,因为此时沙纹波高和波长都较小。 6.2 不同类型沙纹的分布 波浪主导区域分布在近岸水深小于10 m的区域,而流主导的区域覆盖湾的中部以及Jervis湾湾口水深大于20 m的海区。Jervis湾波浪主导的沙纹波高(10~14 cm)和沙纹波长(9~12 cm)通常高于流主导的沙纹,且流主导的沙纹在沙纹波高和波长上比波浪主导的沙纹随时间的变化更为平缓。使用U*cwe_NL与U*cwe_Kb在沙纹几何形态上没有明显的差异。 无传输状态主要出现在水动力条件较弱的Jervis湾中部,而弱传输状态覆盖近岸区域。平衡状态主要出现在西南海岸的狭窄的带状海区以及湾口两侧的近岸海区,平衡状态具有较大的沙纹波高和波长。Jervis湾少有破碎状态而没有层移状态。U*cwe仅仅是用于和临界值比较作为判别,以确定底边界状态是否从无传输到弱传输状态,因此低估U*cwe导致底部形态仍然停留在无传输状态,而不是进一步发展到弱传输状态,因此使用U*cwe_NL并无明显不同。 6.3 展望 波状海底微地形根据尺度不同,可分为沙丘等不同类型。本文研究的沙纹尺度较小,波长为几厘米至十几厘米。今后可推广到大尺度沙丘或者沙脊。如南海波长为10 m量级的沙纹和中国苏北浅滩著名的沙脊等。 目前沙纹底边界层模型中底粗糙度、拖曳系数等的计算主要采用参数化方法,这些参数化方案虽然已经较为准确地反映出真实的运动过程,但对起物理机制的把握尚不完备,今后可进一步发展理论模型。 [1] Babanin A V, Young I R, Mirfenderesk H. Field and laboratory measurements of wave-bottom interaction[M]//Presented at the Coasts and Ports: Coastal Living-Living Coast. Adelaide: Institution of Engineers, 2005. [2] Holmedal L E, Myrhaug D. Bed load transport under irregular waves plus current from Monte Carlo simulations of parameterized models with application to ripple migration rates observed in the field [J]. Coastal Engineering, 2004, 51(2): 155-72. [3] Ribberink J S, Al-Salem A A. Sediment transport in oscillatory boundary layers in cases of rippled beds and sheet flow[J]. Journal of Geophysical Research Atmospheres, 1994, 1994(C6): 12707-12728. [4] Werf J J V D, Ribberink J S, O'Donoghue T, et al. Modelling and measurement of sand transport processes over full-scale ripples in oscillatory flow[J]. Coastal Engineering, 2006, 53(8): 657-673. [5] Thorne P D, Davies A G, Bell P S. Observations and analysis of sediment diffusivity profiles over sandy rippled beds under waves[J]. Journal of Geophysical Research Oceans, 2009, 114(C2): 309-321. [6] Nielsen P. Dynamics & geometry of wave-generated ripples[J]. Journal of Geophysical Research, 1981, 86(C7): 6467-6472. [7] Grant W D, Madsen S O. Movable bed roughness in unsteady oscillatroy flow[J]. Journal of Geophysical Research, 1982, 87(C1): 469-481. [8] Smith G A, Babanin A V, Riedel P, et al. Introduction of a new friction routine into the SWAN model that evaluates roughness due to bedform and sediment size changes[J]. Coastal Engineering, 2011, 58(4): 317-326. [9] Li M Z, Amos C L. Predicting ripple geometry and bed roughness under combined waves and currents in a continental shelf environment[J]. Continental Shelf Research, 1998, 18(9): 941-970. [10] Li M Z, Amos C L. SEDTRANS96: the upgraded and better calibrated sediment-transport model for continental shelves[J]. Computers & Geosciences, 2001, 27(6): 619-645. [11] Tolman H L. Subgrid modeling of moveable-bed bottom friction in wind-wave models[J]. Coastal Engineering, 1995, 26(1/2): 57-75. [12] Ardhuin F, Drake T G, Herbers T H C. Observations of wave-generated vortex ripples on the north carolina continental shelf[J]. Journal of Geophysical Research, 2002, 107(10): 7-1-7-14. [13] Grant W D, Madsen O S. Combined wave and current interaction with a rough bottom[J]. Journal of Geophysical Research, 1979, 84(C4): 1797-1808. [14] Grant W D, Madsen O S. The continental-shelf bottom boundary layer[J]. Fluid Mechanics Annual Reviews, 1986, 18(1): 265-305. [15] Signell R P, Beardsley R C, Graber H C, et al. Effect of wave-current interaction on steady wind-driven circulation in narrow, shallow embayments[J]. Journal of Geophisical Research, 1990, 95(C6): 9671-9678. [16] Mellor G L, Donelan M A, Oey L Y. A surface wave model for coupling with numerical ocean circulation models[J]. Journal of Atmospheric & Oceanic Technology, 2008, 25(10): 1785-1807. [17] Wang X H. Tide-induced sediment resuspension and the bottom boundary layer in an idealized estuary[J]. Journal of Physical Oceanography, 2002, 32(4): 3113-3131. [18] Wang X H, Pinardi N, Malacic V. Sediment transport and resuspension due to combined motion of wave and current in the northern Adriatic Sea during a Bora event in January 2001: A numerical modeling study[J]. Continental Shelf Research, 2007, 27(5): 613-633. [19] Song D H, Wang X H, Cao Z Y, et al. Suspended sediment transport in the Deepwater Navigation Channel, Yangtze River Estuary, China, in the dry season 2009: 2. Numerical simulations[J]. Journal of Geophysical Research, 2013, 118(10): 5568-5590. [20] Blumberg, A F, Mellor, G L. A description of a three-dimensional coastal ocean circulation model[M]//Three-Dimensional Coastal Ocean Models. Washington, D.C.:American Geophysical Union, 1987. [21] Lambrechts J, Humphrey C, McKinna L, et al. Importance of wave-induced bed liquefaction in the fine sediment budget of Cleveland Bay, Great Barrier Reef[J]. Estuarine, Coastal and Shelf Science, 2010, 89(2): 154-162. [22] Nielsen P. Suspended sediment concentrations under waves[J]. Coastal Engineering, 1986, 10(1): 23-31. [23] Wang X H. A numerical study of sediment transport in a coastal embayment during winter storms[J]. Journal of Coastal Research, 2001(34): 414-427. [24] Holloway P E, Symonds G, Nunes V R. Observations of circulation and exchange processes in Jervis Bay, New South Wales[J]. Australian Journal of Marine and Freshwater Research, 1992, 43(6): 1487-515. [25] CSIRO. Jervis Bay Baseline Studies Final Report[R]. CSIRO Division of Fisheries, Marmion Research Laboratories, 1994. [26] Miller M C, McCave I N, Komar P D. Threshold of sediment motion under unidirectional currents[J]. Sedimentology, 1977, 24(4): 507-527. [27] Bagnold R A. An approach to the sediment transport problem from general physics[R]. Washington:U. S. Govt. Print. Off.,1966. [28] Gibbs R J, Matthews M D, Link D A. The relationship between sphere size and settling velocity[J]. Journal of Sedimentary Research, 1971, 41(1): 7-18. [29] Li M Z, Amos C L. Sheet flow and large wave ripples under combined waves and currents: their field observation, model prediction and effects on boundary layer dynamics[J]. Continental Shelf Research, 1999, 19(5): 637-663. [30] Salehi M, Strom K. Using velocimeter signal to noise ratio as a surrogate measure of suspended mud concentration[J]. Continental Shelf Research, 2011, 31(9): 1020-1032. [31] Xavier B C, Silva I O, Guimarães L G, et al. Estimation of suspended sediment concentration by acoustic scattering: an experimental and theoretical analysis for spherical particles[J]. Journal of Soils & Sediments, 2014, 14(7): 1325-1333. Developing the wave-current-microtopography coupled model of sediment dynamics and its applications Lu Jing1,2,Xia Changshui2,Teng Yong2,Liu Xuehai2 (1.CollegeofOceanicandAtmosphericSciences,OceanUniversityofChina,Qingdao266100,China;2.KeyLabofMarineScienceandNumericalModeling,TheFirstInstituteofOceanography,StateOceanicAdministration,Qingdao266061,China) Ripple microtopography prevalently exist on coastal beds, which significantly change the bottom stress and then influence the sediment transport. Previous researchers mainly study the wave-dominant ripples and have applied them to the wave modelling. Wave-current combined flow is rarely discussed to generate ripples, and the combined flow-dominant ripples are rarely implemented to hydrodynamic and sediment models. We embedded the University of New South Wales sediment model into the POM model, and connected them with a wave-current interaction bottom boundary model coupled with a microtopography module under combined flow. We developed a wave-current-microtopography coupled model of sedimentology dynamics, and applied this coupled model to Jervis Bay, Australia. Developing stages and types are modeled, and the ripple height and length are simulated. The suspended sediment transport was analyzed under wave-dominant and combined flow separately. Simulated results show that the wave-dominant ripples have longer height and length. Therefore, ripples place an important role on suspended sediment when waves dominate. Through considering roughness that varies with microtopography, this model can predict the abrupt rising of suspended sediment concentration rather than setting an average uniform roughness. sediment dynamical model;wave-current coupling; microtopography; ripples; bottom boundary layer; roughness; suspended sediments 2016-10-14; 2016-12-13。 国家自然科学基金项目(41072176);中央级公益性科研院所基本科研业务费专项(2014T01,2015P03);国家重点研发计划课题(2016YFC0503602,2016YFB0201103,2017YFA0604101,2017YFA0604104);留学回国人员科技活动项目择优资助。 芦静(1982—),女,四川省成都市人,助理研究员,博士,主要从事物理海洋研究、沉积动力学数值模拟。E-mail:lujing@fio.org.cn 10.3969/j.issn.0253-4193.2017.07.002 P731.2 A 0253-4193(2017)07-0012-14 芦静, 夏长水, 滕涌, 等. 波浪-海流-微地形耦合的沉积动力模式建立及应用[J]. 海洋学报, 2017, 39(7): 12-25, Lu Jing, Xia Changshui, Teng Yong, et al. Developing the wave-current-microtopography coupled model of sediment dynamics and its applications[J]. Haiyang Xuebao, 2017, 39(7): 12-25, doi:10.3969/j.issn.0253-4193.2017.07.002
3 Jervis湾沉积模型的建立
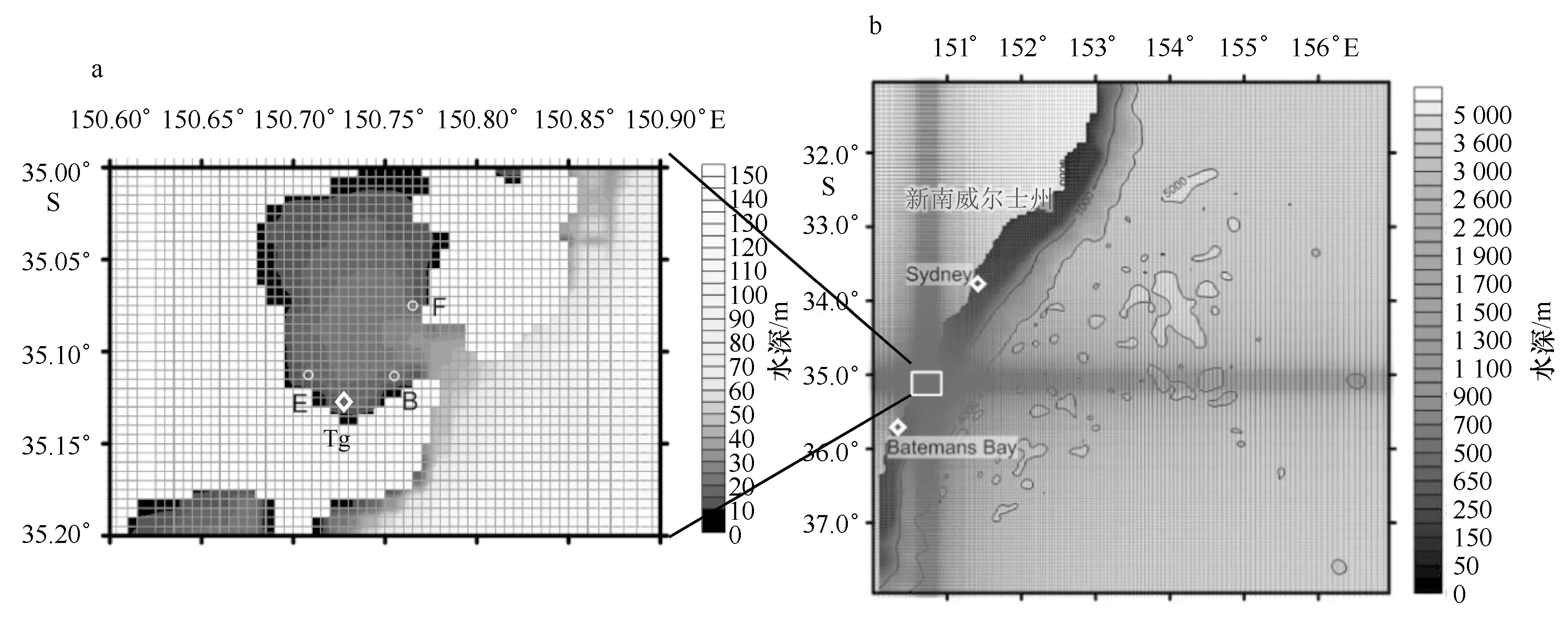
Fig.1 Model domain and grid distribution
a为Jervis湾网格, E站(35.113°S, 150.708°E)位于Jervis湾西南水深11 m处,F站(35.075°S,150.765°E)位于湾口东北部,Tg站为潮位计的布放位置;b为模型区水深和曲线网格系统,其中Jervis湾局部加密
a.Jervis Bay grid Setting, site E(35.113°S, 150.708°E) located off the southwest coast in Jervis Bay with depth of 11 m, and Site F
(35.075°S, 150.765°E) northeast of the bay entrance, the diamond (Tg) denotes the location of the tidal gauge; b. bathymetry and curvilinear grid system with a locally refined grids in Jervis Bay

4 模拟结果

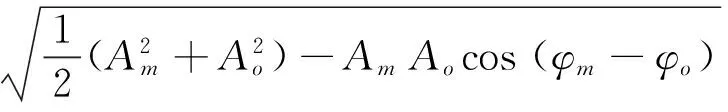




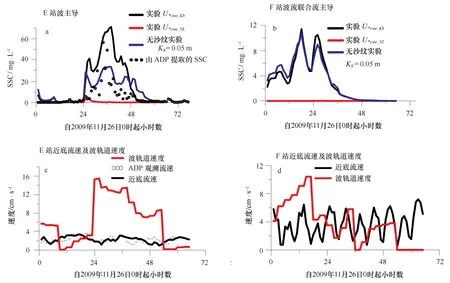


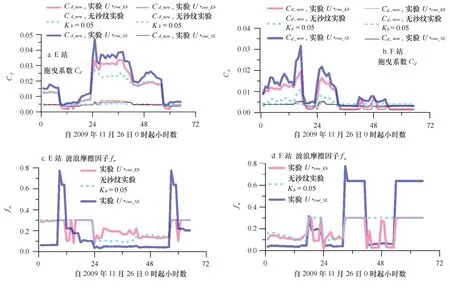
5 讨论

6 结论
