基于探空和SSMI/S资料的AMSR-2海上大气可降水产品检验与评估

尹延通, 刘高飞, 关吉平,, 陈晓颖

(1. 解放军理工大学 气象海洋学院, 江苏 南京 211101; 2. 解放军理工大学 电磁环境效应与电光工程国家级重点实验室, 江苏 南京 210007)

基于探空和SSMI/S资料的AMSR-2海上大气可降水产品检验与评估

尹延通1, 刘高飞1, 关吉平1,2, 陈晓颖1

(1. 解放军理工大学 气象海洋学院, 江苏 南京 211101; 2. 解放军理工大学 电磁环境效应与电光工程国家级重点实验室, 江苏 南京 210007)

利用海岛探空资料和SSMI/S(special sensor microwave imager/sounder)–F16海上大气可降水量产

品对AMER-2 (advanced microwave scanning radiometer-2) 2012年7月—2016年6月的海洋上空大气可降水量产品进行比对检验。结果表明: AMSR-2反演的海上大气可降水量与利用海岛探空资料计算所得值比对的一致性较好, 两者之间平均偏差为0.35 mm; 2012—2016年AMSR-2与SSMI/S-F16可降水月平均值的分布情况在热带辐合带、南太平洋辐合带和南大西洋辐合带可观测到相似的结构和特征, 两者平均偏差为–0.04 mm, 标准偏差为1.21 mm。检验的结果证明了AMSR-2反演的大气可降水产品精度满足产品设计指标, 而误差分析的相应结论对于未来优化水汽反演算法具有重要意义。

海上大气可降水量; AMSR-2(advanced microwave scanning radiometer-2); 探空资料; SSMI/S (special sensor microwave imager/sounder)

水汽是全球水文循环中的重要因素[1], 水汽的输送与降水密切相关[2], 水汽同时也是大气中重要的温室气体[3], 水汽的精确测量对于天气预报、气候研究等具有重要意义[4]。测量大气中水汽含量的设备可以分为地基遥感类、星载遥感类以及原地测量类[5],国际GPS服务机构(Formally International GPS Service, IGS)、全球综合探空档案(integrated global radiosonde archive, IGRA)以及包括SSMI/S (special sensor microwave imager/sounder)等在内的各类卫星产品均提供全球范围内的水汽资料。在海洋上空, 星载微波辐射计测量水汽已经超过25年[6], 目前可用以水汽测量的星载辐射计有DMSP-SSMIS系列, Coriolis上搭载的WindSat、Aqua上搭载的AMSR-E以及GCOM-W1卫星上搭载的AMSR-2(advanced microwave scanning radiometer-2)等。

相比于其他观测手段, 海洋遥感具有观测周期短、时间频率高、覆盖范围广的优势, 能够很好地适应海洋观测的要求[7-8], 是现代海洋大范围同步观测、环境特征分析和资源评估的主要技术手段[9-10],而遥感产品的真实性检验是遥感资料应用的基础和保证[11], 因此遥感数据的准确性问题也受到越来越多的关注。Bock等[12]基于地基GPS数据对SSMI-F13在非洲区域的可降水量产品进行比对, 得出两者平均偏差为2.4～0.7 mm, 标准偏差为3.1～1.2 mm; Chrysoulakis等[13]基于探空资料对AVHRR(advanced very high resolution radiometer )在希腊地区的可降水产品进行比对, 得出均方根误差为4.6 mm; Lindstrot等[14]基于太阳光度计(global AERONET sun photometer measurements)数据、全球GUAN探空数据、地基微波辐射计和德国地基GPS数据对MERIS 可降水数据精度进行评估, 得出平均偏差为1 mm, 标准偏差为1.3～3.7 mm; Lindstrot等[15]基于ARM Nauru地基微波辐射计对SSMI-F13和SSMI-F14在全球范围内的可降水量产品进行检验, 得出平均偏差为–0.48 mm, 标准偏差为1.8 mm; Mears等[6]利用地基GPS数据对多个星载微波辐射计(SSMI/S、AMSR-E和WindSat)的可降水量产品进行检验, 得出了多个微波辐射计反演水汽产品的误差指标。

1 数据及方法

1.1 AMSR-2数据

AMSR-2于2012年5月搭载在GCOM-W1卫星上发射升空。AMSR-2为双极化被动微波辐射计, 采用圆锥扫描的工作方式, 共有6.93、7.3、10.65、18.7、23.8、36.0、89.0 GHz 7个工作频率[16-17], RSS网站采用基于辐射传输模型(RTM)的线性回归算法, 利用18.7、23.8和36.5 GHz水平和垂直极化通道的亮温信息对AMSR-2水汽产品进行反演[18], 本文使用该网站公布的第七版数据, 其空间分辨率为0.25°×0.25°。

1.2 探空资料

本文所使用的探空资料来自美国怀俄明州大学网站(http: //weather.uwyo.edu/upperair/sounding.html),该网站同时公布了利用探空资料计算的可降水值。经检验, 该网站发布的大气可降水值与利用该网站发布的探空资料垂直积分所得结果一致, 本文直接使用该网站公布的大气可降水量进行对比检验。所选探空站点空间分布如图1所示, 表1详细给出了各站点的名称、地理位置及探空设备等信息, 其中探空设备型号信息来自NASS网站(http: //www.ncdc.noaa. gov/data-access/weather-balloon/integrated-global-radi osonde-archive)。

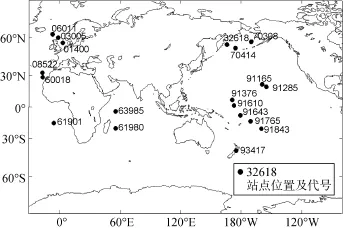
图1 本文所选探空站点的位置Fig. 1 The position of selected radiosonde stations

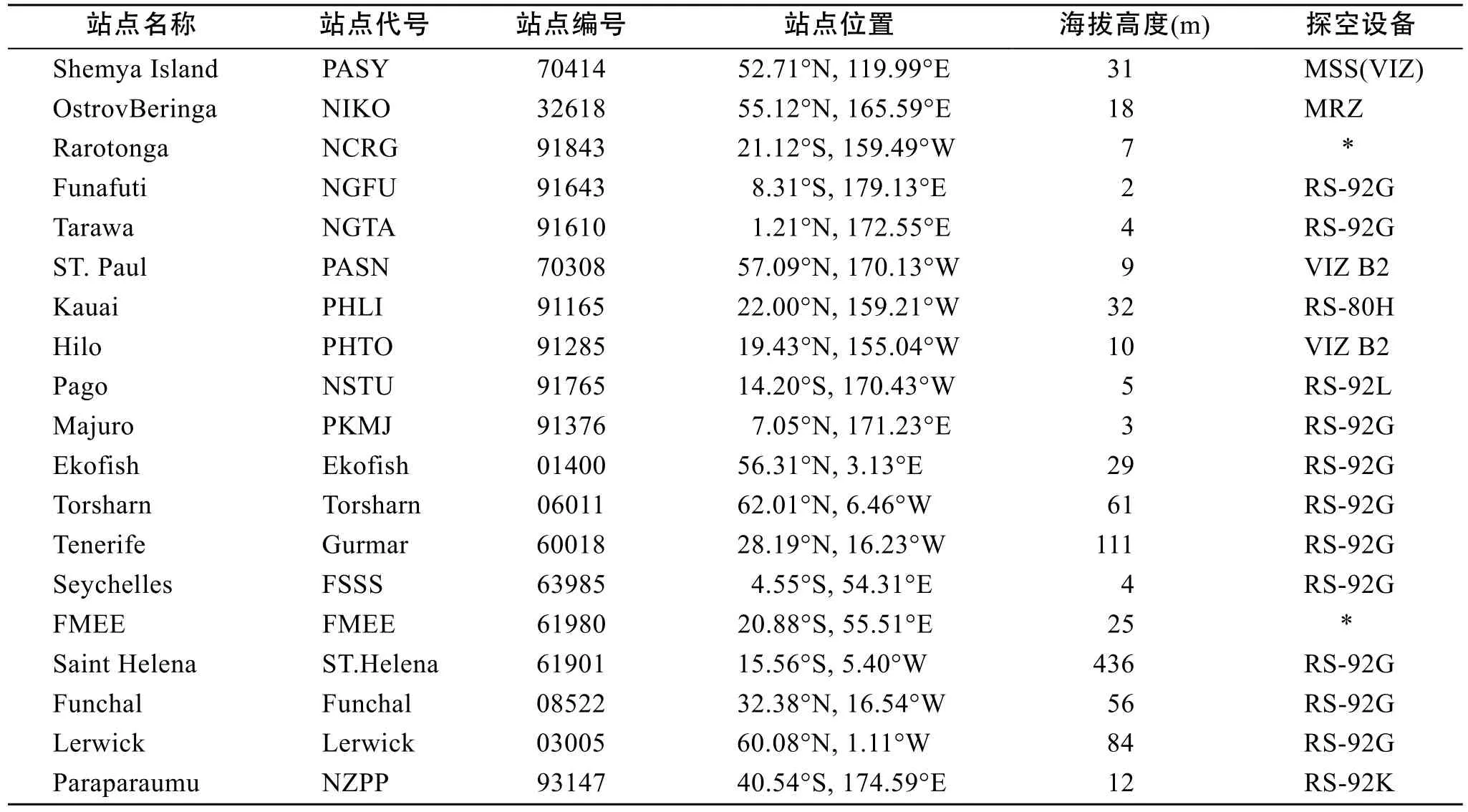
表1 本文所选的探空站点Tab. 1 List of radiosonde stations chosen in this study

1.3 SSMI/S-F16数据

SSMI/S-F16于2003年10月搭载在美国国防气象卫星(DMSP)上发射升空, 在轨运行状况良好, 本文使用的F16水汽产品与AMSR-2水汽产品同为RSS网站公布的第七版数据, 其空间分辨率为0.25°×0.25°, 该产品反演算法的物理基础为海气耦合模型, Wentz[19]基于大量的浮标和探空数据对该模型进行了检验与校正, 而多位学者也对基于该模型反演的SSMI/S-F16水汽产品进行了检验与评估: Sun等[20]对DMSP-F16 SSMI/S 2005年12月—2006年2月各项反演产品的精度进行了全面评估, 其中可降水产品平均偏差为–0.75 mm, 标准偏差为0.62 mm; Mears等[6]利用地基GPS信号延迟计算所得可降水数据对一系列星载微波辐射计反演可降水产品进行了比对, 得出F16 2004—2009年可降水产品平均偏差为0.54 mm, 标准偏差为1.91 mm, 并指出该产品在检验期间内精度未发生明显变化。鉴于探空站点空间分布的局限性, 本文选取RSS公布的SSMI/S-F16 2012年7月—2016年6月的月平均数据对验证数据进行补充, 以完成AMSR-2可降水产品在全球范围内的精度评估。

1.4 比对数据海拔订正及样本匹配方法

统一战线促进社会全面发展的价值体现在统一战线既助力共同体经济基础的发展，也助力共同体上层建筑的完善。统一战线是为经济基础服务重要手段和社会政治发展重要目标的统一，是调处关系手段与实现和谐目标的统一，是发扬人民民主手段与实行人民民主专政目标的统一［13］。新时代，统一战线在国家治理中促进中国特色社会主义民主发展、制度定型和关系整合，体现出自身促进社会全面发展的战略功能。其中，很重要的内容就是促进民主政治发展。由于政治的核心内容是权力配置，统一战线作为政治联盟，其核心功能是协调权力配置关系，即扩大公民有序政治参与、满足民主需求、实现政治发展。其核心机制是依托社会主义协商民主制度来实现民主功能。

海拔高度的差异会在两种水汽测量设备的比对中引入误差, 因此需要在比对之前对水汽测量数据进行海拔订正[21], 本文采用Buehler等[22]提出的经验订正模型对卫星产品进行了海拔订正。

SSMI/S-F16与AMSR-2可降水产品的月平均产品同为1 440×720的格点数据, 两者对应格点分别代表同一区域某个月水汽测量的平均值, 因此无需对数据进行时间窗口的选取, 可直接将两者对应格点数据进行比对。

这里重点对AMSR-2水汽产品与探空资料的比对方法进行说明: 参照John等[23]、Jackson等[24]对于时间窗口的的选取, 以2 h 为时间窗口, 对卫星数据和探空数据进行时间匹配; 由于陆面污染的影响,需对卫星数据进行预处理以便完成与探空资料的空间匹配, 多为学者选取距离探空站点最近的网格数据作为该站点的水汽测量值[11-12](简称最近原则), Mears等[6]提出使用二维线性拟合的方法对卫星数据在海岛探空处的缺测值进行补充(下文称线性拟合方法), 为对两种预处理方法进行比较, 本文分别采用两种方法对卫星数据进行处理, 并对相应结果进行说明。

2 比对结果

2.1 与探空数据比对总体情况

采用不同预处理方法所得误差的统计结果如表2所示。从表2可见, 采用不同预处理方法对平均偏差及线性相关系数影响不大, 但就均方根误差及标准偏差而言, 采用最近原则所得结果明显大于线性拟合方法, 且两者差值可达10%, 这可能是由于采用距离最近原则匹配的卫星反演值距离探空站点较远, 不能较好地代表探空站点处的水汽值, 而采用线性拟合方法减弱了个别反演值对于整体比对结果的影响, 这在一定程度上减小了时空不匹配造成的随机误差。鉴于此, 本文将统一采用线性拟合方法对卫星数据进行预处理, 并对所得数据进行分析。

表2 误差统计结果Tab. 2 Summary of differences

在对误差样本进行统计时, 发现个别误差超过±20 mm甚至达到±40 mm, 虽然个数较少, 但对AMSR-2反演精度评估的总体结果影响较大, 这里根据3σ原则[25], 将距离偏差平均值正负3倍标准偏差以外的351个样本作为粗大误差数据进行了剔除,剔除后标准偏差减小了0.5 mm。误差剔除前后AMSR-2可降水产品反演值与19个海岛探空资料计算值的比对结果如图2所示, 从图2可见, 散点大多沿y=x(红色虚线)对称分布, 显示AMSR-2反演值与探空计算值比对一致性较好。

2.2 误差月际变化和逐月演变情况

由于同一季节南北半球水汽分布变化规律不同,这里分别以误差在南北半球的变化情况为研究对象,对AMSR-2水汽产品反演精度随时间的变化情况展开分析。

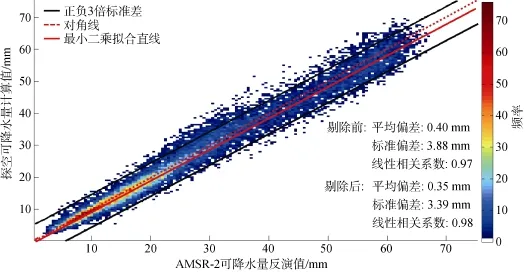
图2 AMSR-2反演值与探空计算值比对结果Fig. 2 The comparison between AMSR-2 and radiosonding measurements

为分析南北半球误差季节性变化规律, 这里给出了AMSR-2与探空之间误差的月际变化情况(图3)。从图3可见, 北半球各月平均偏差在[0, 0.5] mm, 标准偏差在[2.5, 3.5] mm, 误差季节性变化较为明显,平均偏差和标准偏差最大值均出现在7月和8月; 对于南半球而言, 平均偏差几乎全年位于0.5 mm以上,显示AMSR-2反演值在南半球全年均大于探空计算值, 而标准偏差全年均大于3.5 mm, 且季节性变化不明显。这可能是由于南北半球探空站点的纬度分布情况不同造成的, 北半球站点纬度分布较为分散,且多数站点处在中高纬度地区, 水汽季节性变化较为明显且量值较小; 南半球站点纬度分布相对集中,多数位于热带地区(0°～23.5°S), 因此全年水汽充沛, 可降水量值较大且季节性变化不明显; 经统计, 南北半球所选站点可降水测量均值分别为40 mm和25 mm,而Mears等[6]指出卫星水汽产品的精度会随着测量值的增大而有所下降, 这可能是导致南北半球误差在全年分布差异较大的主要原因。

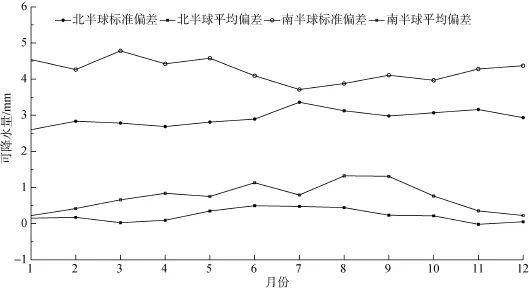
图3 AMSR -2反演值与探空计算值之间误差的月际变化Fig. 3 Inter-monthly variation of the comparison results between AMSR-2 and radiosonding

AMSR-2反演值与探空计算值之间误差的逐月演变曲线如图4所示。从图4可见, 南半球平均偏差变化幅度较大, 这可能是水汽反演精度随测量值增大有所下降引起, 而北半球平均偏差在2014年上半年发生明显的跃动, 在对各站点误差进行统计分析时, 发现91165号探空站可能由于更换了探空设备或数据处理方法导致平均偏差在2014年从–3 mm变化至+1 mm, 这有可能是引起总体偏差发生变化的主要原因; 南北半球标准偏差逐月变化曲线以3.5 mm水平线为对称轴基本呈对称分布, 而南北半球水汽测量平均值的逐月变化曲线也呈现相似的特征(图5), 这表明标准偏差和水汽的测量值之间存在较为密切的相关性。

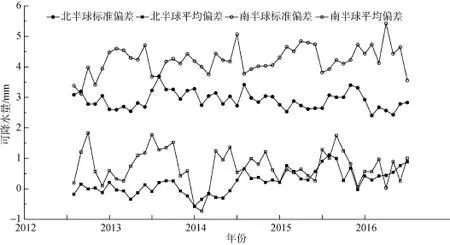
图4 AMSR -2反演值与探空计算值之间误差逐月演变Fig. 4 Monthly variation of the comparison between AMSR-2 and radiosonding

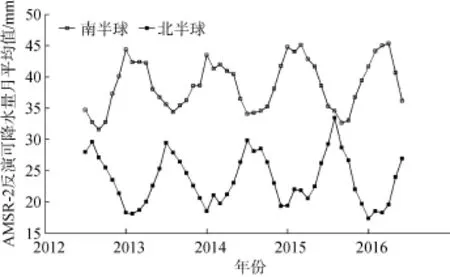
图5 AMSR -2可降水测量月平均值逐月演变Fig. 5 Monthly variation of AMSR-2 TPW

2.3 误差空间分布

AMSR-2水汽产品与探空比对误差的空间分布情况见图6, 表3详细给出了各个站点的经纬度、误差统计结果以及样本数。从平均偏差的分布情况(图6)可见, AMSR-2在大部分海域略大于探空计算值,且平均偏差在1 mm左右, 这与Mears等[6]基于地基GPS数据对多颗卫星可降水数据进行比对得到的结果相似。

从标准偏差的分布情况(图6)可见, 标准偏差具有明显的纬向分布特征, 高纬度地区标准偏差不超过2 mm, 而在低纬度地区(除61901号探空站)标准偏差均达到了3 mm, 这与Mears等[6]基于地基GPS数据对其他卫星(如AMSR-E和WindSat等)水汽产品进行检验的结果相同, 即卫星反演水汽值在与低纬度地区的地基GPS测站(如DGAR测站、KWJ1测站、SANO测站和SEY1测站等)进行比对时, 标准偏差明显高于地处中高纬度地区的测站。

2.4 误差与地球物理参数之间的相关性

为进一步评估AMSR-2水汽反演精度, 这里对AMSR-2反演值与探空计算值之间误差与可降水量、风速、海表面温度、云中液态水以及雨强之间的相关关系进行了计算。与Mears等[6]得出的结论相同,误差与海表面温度、云中液态水和雨强之间无明显相关关系, 基于此, 本节主要对误差与可降水量和风速的相关关系展开分析, 图7给出了平均偏差、标准偏差随可降水量、风速的变化情况, 其中小棒代表标准偏差, 长度代表标准偏差的大小, 带方框的曲线代表平均偏差。

从图7可见, 平均偏差在[0, 40] mm测量区间内均靠近零轴, 表明AMSR-2在40 mm以下测量区间内反演效果较好; 平均偏差在[40, 60] mm测量区间内均分布在零轴以上, 表明AMSR-2在该区间内反演值高于探空计算值; 而当测量值大于60 mm时,平均偏差急剧下降, 显示AMSR-2反演值在高值区间明显小于探空计算值; 标准偏差在[0, 30] mm测量区间内随可降水量值增大而增大, 而在30 mm以上区间变化不明显, 表明测量值在低值区间内对标准偏差影响较为明显。

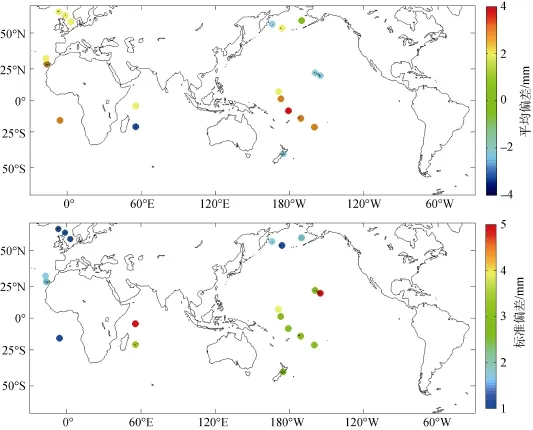
图6 AMSR-2与探空数据之间平均偏差和标准偏差的分布情况Fig. 6 Distribution of mean bias and standard deviations between AMSR-2 and radiosonding

表3 各探空站点误差统计结果Tab. 3 Difference statistics of each station

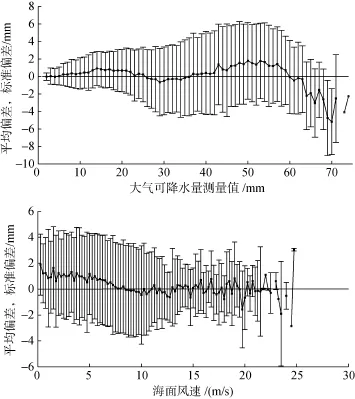
图7 AMSR-2与探空之间平均偏差和标准偏差随可降水测量值及风速变化情况Fig.7 Mean and standard deviation of AMSR-2-RS TPW differences as a function of mean TPW and wind speed

从图7可见, 风速处于[5, 10] m/s时, 平均偏差随风速明显下降。Mears等[6]将SSMI、SSMI/S和AMSR-E水汽产品与地基GPS进行比对时发现, 当风速处于[4, 11] m/s时, 卫星反演水汽产品的平均偏差与风速存在相同的相关关系。多位学者对造成这一现象的原因进行了探究: Sohn和Smith[26]指出统一化的海洋微波反演算法(UMORA)在对水汽进行反演时, 过高估计了风速的影响, 导致反演的水汽值随风速增加而减小; Wang等[27]指出这是由于高频率通道(例如22 GHz 和37 GHz)对于低风速不敏感, 在统一化的海洋微波反演算法(UMORA)引入较大的不确定性引起的; Meissner和Wentz[28]指出这是由于在利用微波亮温反演水汽时, 海面对于微波的反射和散射作用, 在反演中引入了一个与风速相关的误差导致的。

2.5 与SSMI/S-F16比对结果

这里对2012年6月—2016年6月的AMSR-2与SSMI/S-F16的月平均可降水产品进行了比对, 结果表明AMSR-2可降水数据与SSMI/S-F16可降水数据比对的一致性较好, 两者48个月平均值之间平均偏差为–0.04 mm, 标准偏差为1.21 mm(偏差为AMSR-2反演值减去F16反演值, 文中下同), 通过分析两者可降水月平均值在2012—2016年期间的分布情况, 可发现两者在热带辐合带(ITCZ)、南太平洋辐合带(SPCZ)和南大西洋辐合带(SACZ)具有相似的结构和特征, 限于篇幅不再进行详细说明, 这里重点对两者之间平均偏差的分布情况进行分析。

由于各年AMSR-2水汽产品的测量值及偏差情况基本类似, 这里选取AMSR-2与F16水汽产品在2014年的比对结果进行分析。图8为2014年AMSR-2可降水测量平均值与平均偏差在2014年1月、7月及全年的分布情况, 从图8可见, AMSR-2 与F16可降水数据之间误差分布在±1 mm以内, 大部分区域误差在±0.5 mm以内; 在低纬度地区AMSR-2 测量值略低于F16测量值, 在中纬度地区AMSR-2 测量值略高于F16测量值。对比分析测量平均值和平均偏差在1月份分布情况可见, 测量平均值大于60 mm的海域(例如北印度洋和西太平洋海域)对应的平均偏差为负值且绝对值大于0.8 mm, 测量值在[30, 50] mm的海域(例如南印度洋、北太平洋和南太平洋海域)平均偏差多为正值且大于0.8 mm。

对比分析AMSR-2可降水产品测量值及误差在7月份和全年的分布情况, 可以得出与1月份相同的结论。这进一步印证了AMSR-2反演精度随测量值发生变化(图7)的结论, 即AMSR-2在[0, 40] mm测量区间内反演精度较好, 在[40, 60] mm测量区间内反演值偏大, 60 mm以上测量区间内反演值偏小。

3 结论

本文以海岛探空资料和SSMI/S-F16可降水月平均资料为验证数据, 对AMSR-2反演的海洋上空大气可降水量的产品精度进行了全面评估, 分析了AMSR-2反演值与探空计算值之间误差总体情况、平均偏差和标准偏差逐月演变曲线、各站点误差空间分布、误差与地球物理参数的相关性以及与SSMI/SF16月平均数据比对误差空间分布情况。

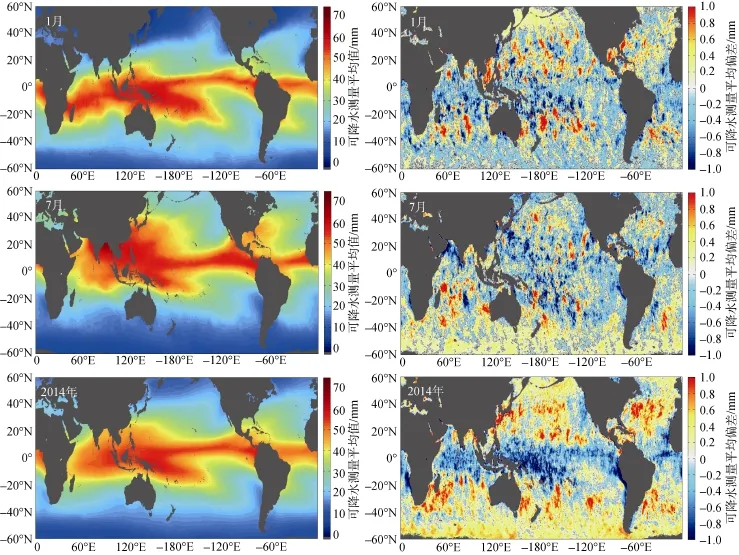
图8 2014年1月份、7月份及全年AMSR-2可降水测量平均值与平均偏差分布情况Fig. 8 Distribution of mean value and bias of AMSR-2 TPW in January, July, and the entire year

结果表明, AMSR-2反演海面可降水量与海岛探空资料比对的一致性较好, 两者之间平均偏差为0.35 mm, 标准偏差为3.36 mm, 均方根误差为3.38 mm;从误差逐月变化曲线可见, 北半球平均偏差和标准偏差季节性变化较为明显, 且均在7月份和8月份达到最大, 南半球平均偏差和标准偏差在全年均大于北半球, 季节性变化不明显; 从误差的空间分布情况可以看出, AMSR-2在大部分海域略大于探空计算值, 标准偏差随纬度变小而增大; 从误差与测量值的相关关系分析可以看出, AMSR-2在可降水低值区间反演精度较好, [40, 60] mm区间反演值偏大, 60 mm以上区间反演值偏小; 与SSMI/S-F16可降水月平均值比对的偏差分布显示, AMSR-2反演值在低纬度地区略低于SSMI/S-F16, 在中纬度地区略高于SSMI/ S-F16, 进一步说明了AMSR-2在不同测量区间反演精度的变化情况。

随着技术的进步, 卫星遥感数据在大气科学研究中, 特别是洋面区域, 将发挥越来越重要的作用。本论文基于探空数据和SSMI/S-F16水汽产品对AMSR-2水汽反演精度进行了检验, 以期对全球洋面水汽的分布特点具有更加全面的认识, 相应结果对于更好地使用该水汽反演产品, 避免可能出现的误差具有一定的指导意义和应用价值。

[1] Olivier B, Pascal W, Wang J, et al. A high-quality, homogenized, global, long-term (1993–2008) DORIS precipitable water data set for climate monitoring and model verification[J]. Journal of Geophysical Research Atmospheres, 2014, 119(12): 7209-7230.

[2] 齐庆华. 西北太平洋水汽输送异常及其与中国夏季降水的耦合模态[J]. 海洋科学, 2009, 33(9): 35-41. Qi Qinghua. The spatio-temporal characters of the northwest Pacific water vapor flux and its coupled modes with the summer rainfall in China[J]. Marine Sciences, 2009, 33(9): 35-41.

[3] Mengistu T G, Blumenstock T, Hase F. Observations of precipitable water vapour over complex topography of Ethiopia from ground-based GPS, FTIR, radiosonde and ERA-Interim reanalysis[J]. Atmospheric Measurement Techniques, 2015, 8(8): 3277-3295.

[4] Ohtani R, Naito I. Comparisons of GPS-derived pre-cipitable water vapors with radiosonde observations in Japan[J]. Journal of Geophysical Research Atmospheres, 2000, 105(D22): 26917-26930.

[5] Wang Junhong, Zhang Liangying. Systematic errors in global radiosonde precipitable water data from comparisons with ground-based GPS measurements[J]. Journal of Climate, 2008, 21(10): 2218-2238.

[6] Mears C A, Wang J, Deborah S, et al. Intercomparison of total precipitable water measurements made by satellite-borne microwave radiometers and ground-based GPS instruments[J]. Journal of Geophysical Research Atmospheres, 2015, 120(6): 2492-2504.

[7] 韩震, 陈西庆, 恽才兴. 海洋高光谱遥感研究进展[J].海洋科学, 2003, 27(1): 22-25. Han Zhen, Chen Xiqing, Yun Caixing. Research progress of marine hyperspectral remote sensing[J]. Marine Sciences, 2003, 27(1): 22-25.

[8] 何娜, 张祖强, 肖贤俊, 等. 海洋环流模式中卫星遥感资料同化的应用进展[J]. 海洋科学, 2008, 2(12): 92-96. He Na, Zhang Zuqiang, Xiao Xianjun, et al. Advancement in application to satellite data assimilation in the ocean circulation model[J]. Marine Sciences, 2008, 32(12): 92-96.

[9] 应晨璐, 董庆, 薛存金, 等. 大区域海洋遥感数据处理方法研究[J]. 海洋科学, 2014, 38(8): 116-125. Ying Chenlu, Dong Qing, Xue Cunjin, et al. Researches of processing methods on large-scale marine remote sensing data[J]. Marine Sciences, 2014, 38(8): 116-125.

[10] 郑崇伟, 李崇银, 杨艳, 等. 巴基斯坦瓜达尔港的风能资源评估[J]. 厦门大学学报: 自然科学版, 2016, 55(2): 210-215. Zheng Chongwei, Li Chongying, Yang Yan, et al. Analysis of wind energy resource in the Pakistan's Gwadar Port[J]. Journal of Xiamen University (Natural Science), 2016, 55(2): 210-215.

[11] 刘瑞霞, 师春香, 刘杰. 直方变差图理论在卫星产品质量检验空间配准中的应用[J]. 遥感学报, 2009, 13(2): 307-312. Liu Ruixia, Shi Chunxiang, Liu Jie.The application of Histo-variogram method in spatial matching of satellite data validation[J]. Journal of Remote Sensing, 2009, 13(2): 307-312.

[12] Bock O, Bouin M, Walpersdorf A, et al. Comparison of ground-based GPS precipitable water vapour to independent observations and NWP model reanalyses over Africa[J]. Quarterly Journal of the Royal Meteorological Society, 2007, 133(629): 2011-2027.

[13] Chrysoulakis N, Kamarianakis Y, Xu L, et al. Combined use of MODIS, AVHRR and radiosonde data for the estimation of spatiotemporal distribution of precipitable water[J]. Journal of Geophysical Research Atmospheres, 2008, 113(D5): 79-88.

[14] Lindstrot R, Preusker R, Diedrich H, et al. 1-D-Var retrieval of daytime total columnar water vapour from MERIS measurements[J]. Atmospheric Measurement Techniques, 2012, 5(3): 631-646.

[15] Lindstrot R, Stengel M, Schröder M, et al. A global climatology of total columnar water vapour from SSM/I and MERIS[J]. Earth System Science Data, 2014, 6(1): 221-233.

[16] 奚萌, 宋清涛, 林明森, 等. 西北太平洋多源微波辐射计海表温度数据交叉比对分析[J]. 海洋学报, 2016, 38(7): 32-47. Xi Meng, Song Qingtao, Lin Mingsen, et al. Intercomparison analysis of muti-microwave radiometer sea surface temperature data for the Nrothwest Pacific[J]. Haiyang Xuebao, 2016, 38(7): 32-47.

[17] 叶勤玉, 柴琳娜, 蒋玲梅, 等. 利用AMSR2和MODIS数据的土壤冻融相变水量降尺度方法[J]. 遥感学报, 2014, 18(6): 1147-1157. Ye Qinyu, Chai Linna, Jiang linmei, et al.A disaggregation approach for soil phase transition water content using AMSR2 and MODIS product[J]. Journal of Remote sensing, 2014, 18(6): 1147-1157.

[18] Wentz F J, Meissner T. Supplement 1 Algorithm Theoretical Basis Document for AMSR-E Ocean Algorithms, RSS Tech. Rep[R]. Santa Rosa, California: Remote Sensing System, 2007.

[19] Wentz F J. A well-calibrated ocean algorithm for special sensor microwave/imager[J]. Journal of Geophysical Research, 1997, 102(C4): 8703-8718.

[20] Sun N, Weng F. Evaluation of special sensor microwave imager/sounder (SSMIS) Environmental Data Records[J]. IEEE Transactions on Geoscience & Remote Sensing, 2008, 46(4): 1006-1016.

[21] Van Malderen R, Brenot H, Pottiaux E, et al. A multi-site intercomparison of integrated water vapour observations for climate change analysis[J]. Atmospheric Measurement Techniques, 2014, 7(2): 1075-1151. [22] Buehler S A, Stman S, Melsheimer C, et al. A multi-instrument comparison of integrated water vapour measurements at a high latitude site[J]. Atmospheric Chemistry & Physics, 2012, 12(8): 10925-10943.

[23] Alishouse J C, Snyder S A, Vongsathorn J, et al. Determination of oceanic total precipitable water from the SSM/I[J]. IEEE Transactions on Geoscience & Remote Sensing, 1990, 28(5): 811-816.

[24] Jackson D L, Stephens G L. A study of SSM/I-derived columnar qater vapor over the global oceans[J]. Journal of Climate, 1995, 8(8): 2025-2038.

[25] Pukelsheim F. The Three Sigma Rule[J]. The AmericanStatistician, 1994, 48(2): 88-91.

[26] Sohn B J, Smith E A. Explaining Sources of Discrepancy in SSM/I Water Vapor Algorithms.[J]. Journal of Climate, 2003, 16(20): 3229-3255.

[27] Wang Yu, Fu Yunfei, Liu Guosheng, et al. A new water vapor algorithm for TRMM Microwave Imager (TMI) measurements based on a log linear relationship[J]. Journal of Geophysical Research Atmospheres, 2009, 114(D21): 6149-6150.

[28] Meissner T, Wentz F J. The emissivity of the ocean surface between 6 and 90 GHz over a large range of wind speeds and earth incidence angles[J]. IEEE Transactions on Geoscience & Remote Sensing, 2012, 50(50): 3004-3026.

Validation and evaluation of AMSR-2-derived total precipitable water over sea surface using radiosonde and SSMI/S data

YIN Yan-tong1, LIU Gao-fei1, GUAN Ji-ping1,2, CHEN Xiao-ying1
(1. Institute of Meteorology and Oceanography, PLA University of Science and Technology, Nanjing 211101, China; 2. National Key Laboratory on Electromagnetic Environmental Effects and Electro-optical Engineering, PLA University of Science and Technology, Nanjing 210007, China)

Oct.21, 2016

total precipitable water over sea surface; advanced microwave scanning radiometer-2; radiosonde data; special sensor microwave imager/sounder

A validation of the total precipitable water (TPW) over sea surface derived from advanced microwave scanning radiometer-2 (AMSR-2) from July 2012 to June 2016 is conducted by comparing the special sensor microwave imager/sounder (SSMI/S-F16) and island radiosonde data. It is shown that the amount of TPW derived from AMSR-2 is consistent with that of the island radiosonde data with a mean difference of 0.35 mm. The structures and the characteristics of monthly mean TPW derived from AMSR-2 are quite similar to those of SSMI/S-F16 in the Inter-tropical Convergence Zone, South Pacific Convergence Zone, and South Atlantic Convergence Zone from 2012 to 2016. The mean difference between AMSR-2 and SSMI/S-F16 is –0.04 mm, while the standard deviation is 1.21 mm.

P426

A

1000-3096(2017)04-0065-10

10.11759/hykx20161021002

(本文编辑: 刘珊珊)

2016-10-21;

2016-11-21

国家自然科学基金(41076012, 41276019, 41475021); 国家自然科学青年基金 (41305137)

[Foundation: National Natural Science Foundation of China, No. 41076012, 41276019, 41475021; Young Scientists Fund of the National Natural Science Foundation of China, No.41305137]

尹延通(1991-), 男, 河南南阳人, 硕士研究生, 主要从事卫星遥感产品评估及应用方面研究, 电话: 15195850144, E-mail: 1044147875@qq.com; 关吉平, 通信作者, 副教授, 硕士生导师, 电话: 025-80830625, E-mail: 191686624@qq.com