考虑设备劣化及随机需求的最优生产周期模型
2017-07-07周炳海刘玉旺
周炳海,刘玉旺
(同济大学 机械与能源工程学院,上海 201804)
考虑设备劣化及随机需求的最优生产周期模型
周炳海,刘玉旺
(同济大学 机械与能源工程学院,上海 201804)
针对生产过程中由于设备劣化引起产品缺陷率增大以及顾客需求波动问题,构建了综合考虑设备劣化和需求随机的最优生产周期模型。利用伽马过程对上游生产单元的劣化过程进行建模,并假设当其劣化量达到中间某一水平时,生产活动从“受控”转变为“失控”状态;以此为基础,在假设下游需求随机的条件下,以最小化单位产品的总成本为优化目标建立了数学模型;借助数值实例演示了本模型的有效性,并对相关参数作了敏感性分析。分析结果表明:本文所提模型对于描述设备劣化程度对产品质量的影响,降低企业运行成本(库存、返工、维护等)有一定的指导意义。
设备劣化;伽马过程;随机需求;缓冲;优化
在实际制造系统中,随着生产设备的运行,其劣化程度逐渐加剧,使得加工产品的不合格率也随之增大[1-3]。此外,顾客的需求模式逐渐从以往的“大批量、单一化”向“多品种、小批量”转变,这一转变对如何保障制造过程的平稳性提出了新的挑战。合理地决策设备的运行周期以及缓冲区的容量是解决上述两个问题的有效途径。
许多文献将生产系统简化为一个两设备一缓冲系统,以便将设备的劣化过程、维护策略以及缓冲区的容量控制同时纳入一个数学模型中综合考虑。Chelbi等假设对上游设备进行定期预防性维护,建立了缓冲区库存S和预防性维护间隔T的联合优化模型[4]。在此基础上,Rezg等又考虑一个生产周期内缓冲开始建立的时刻A,将模型扩展为(T,S,A)的三维联合优化模型[5]。成国庆等利用几何过程来刻画上游生产设备的退化特征,研究了修复非新条件下的带缓冲区的生产系统维修更换策略[6]。Karamatsoukis等假设上游设备有m个工作状态,1个失效状态,为其最优的预防性维护建立了离散时间的Markov决策模型,即所谓的“控制限”策略[7-8]。之后Karamatsoukis等又将该模型扩展至上下游设备均随时间逐渐劣化并均可能发生失效的情形[9]。Sana[1]考虑到生产过程的不完美性(即存在不合格品),在假设对系统进行定期预防性维护的条件下确定了使单位产品总成本最小的最优库存水平[3]。Radhoui同样考虑一个不完美生产系统,为其质量控制和预防性维护作了联合优化[10]。文献[11-12]则是考虑一类存放时随时间逐渐劣化的产品,对经典的EPQ模型进行了扩充,两者的不同在于分别假设维护时间为定值和随机量。
上述文献虽然都考虑到了上游设备的劣化、失效及对应的维护策略(TBM[13]或CBM[14]),但它们大都假设生产出的产品均是完美的(文献[3,9]除外),并未将设备的劣化状态与产品质量两者联系起来,并且在对缓冲区容量进行优化时都假设下游的需求速率恒定。本文以生产-缓冲-装配系统为研究对象,假设随着上游生产单元劣化量的增大,产品的不合格率也随之增大,并且下游装配单元的需求速率是一随机量,以单位产品总成本最小为目标函数,建立并求解了数学模型。
1 问题描述及模型构建
1.1 问题域描述
考虑一个由生产单元(P)、装配单元(A)和中间缓冲区(B)组成的系统,生产单元生产出的产品配件存放于缓冲区,装配线以随机的需求速率X从缓冲区取用配件进行装配(如图1)。

图1 生产-缓冲-装配系统示意图Fig.1 Structure of the production-buffer-assembly system
为进一步描述研究问题域,作如下假设:
1)在t=0时刻,生产单元以速率p开始生产,装配单元以随机的需求速率X(p0≤X≤p)取用配件,p>X,则缓冲区库存以速率p-X进行累积;经过生产周期T1之后,生产单元停止生产,装配单元仍以速率X消耗配件,直至时刻T2缓冲耗尽。
2)随着生产活动的进行,生产单元会发生劣化,假设其劣化过程为连续过程。当t<τ时,生产活动处于受控状态,产品不合格率为a;当τ≤t
3)对生产单元进行连续监测,在生产过程中其不会发生失效(即生产过程中不会发生X(t)>DF)。
4)在正常生产周期T1结束后,对不合格品统一进行返工。
5)存放在缓冲区的产品不发生劣化或报废。
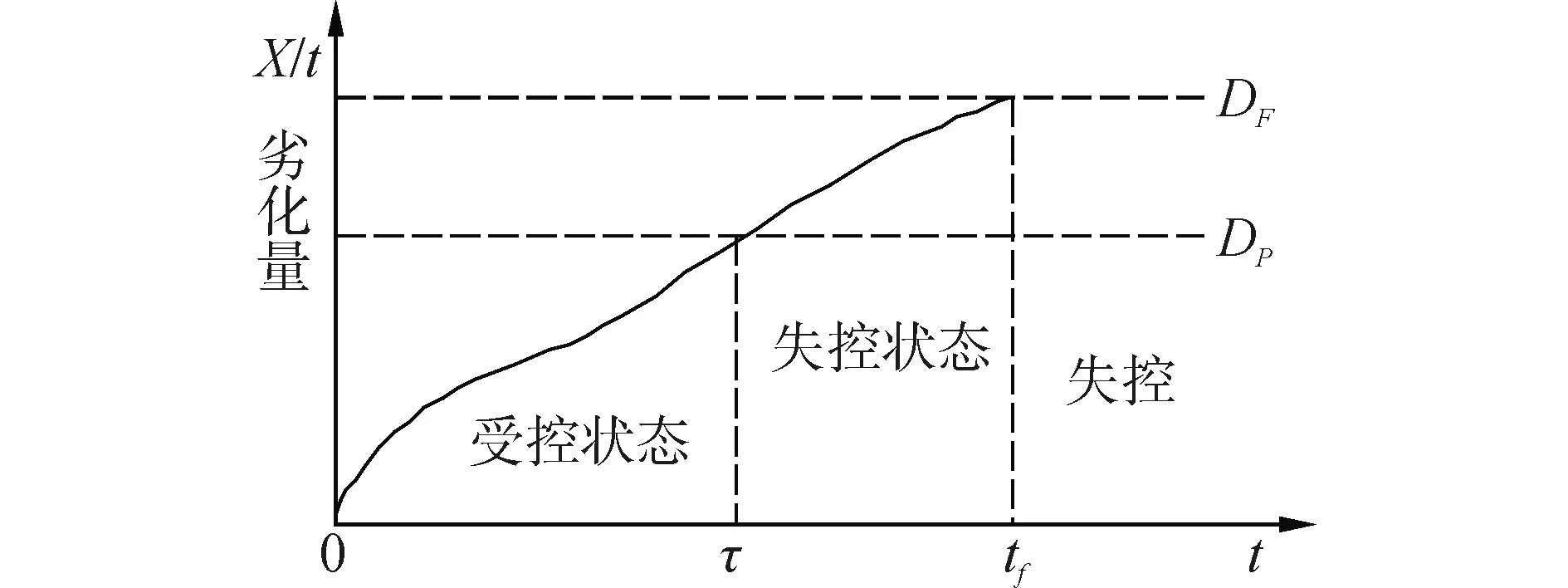
图2 生产单元的劣化过程及生产过程的状态转变示意图Fig.2 Schematic illustration of the degradation process and the transition of production state
1.2 生产过程的不完美性建模
考虑到劣化过程的不可逆性,而伽马过程有非负的独立增量特性,因此我们选用定态伽马过程(形状参数α(t)=αt,尺度参数β)来刻画设备的劣化量随时间逐渐增大这一特性。设X(t)表示t时刻设备的劣化量,则其概率密度函数可表示为[15]
(1)
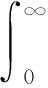
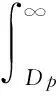
(2)
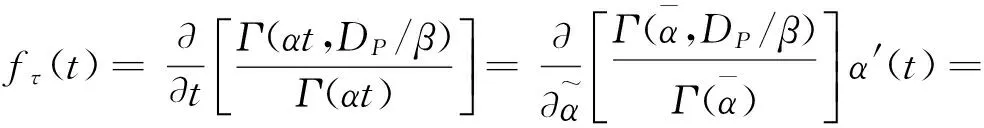
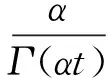
(3)
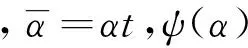
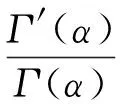
(4)
1.3 随机需求条件下的成本分析
1.3.1 库存持有成本
根据生产周期长度与生产单元状态转变时刻的相对大小关系,可分为以下两种情况。
情形1τ>T1,生产过程全部处于受控状态,产品不合格率为a,生产结束后对设备进行预防性维护,并假设修复如新。任一时刻合格品的库存水平可通过下式表达:
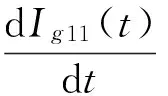
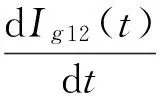
Ig12(T1)=[(1-a)p-X]T1,Ig12(T2)=0
利用上述边界条件,可以求得
Ig11(t)=[(1-a)p-X]t, 0≤t≤T1
(5)
Ig12(t)=-Xt+(1-a)pT1,T1≤t≤T2
(6)
由Ig12(T2)=0,可以得到
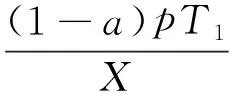
(7)
则合格品的库存持有成本为
(8)
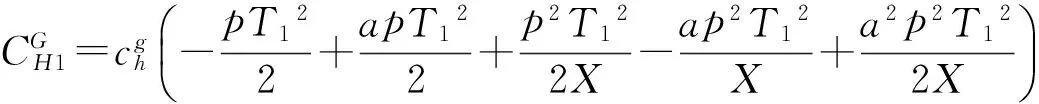
不合格品的库存水平可通过下式表达:
Ir11(t)=apt,0≤t≤T1
(9)
则不合格品的库存持有成本为
(10)
情形2τ≤T1
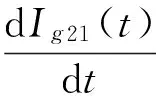
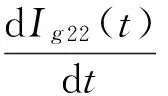
Ig22(τ)=[(1-a)p-X]τ
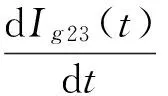
Ig23(T1)=Ig22(T1),Ig23(T2)=0
利用上述边界条件,可以求得
Ig21(t)=[(1-a)p-X]t, 0≤t≤τ
(11)
Ig22(t)=[(1-b)p-X]t+(b-a)pτ,
τ≤t≤T1
(12)
Ig23(t)=-Xt+(1-b)pT1+(b-a)pτ,
T1≤t≤T2
(13)
由Ig23(T2)=0,可以得到
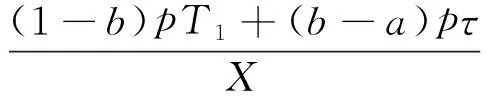
(14)
则合格品的库存持有成本为
(15)
化简得
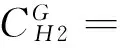
不合格品的库存水平可通过下式表达:
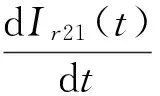
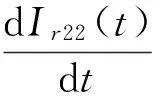
利用边界条件,可求得
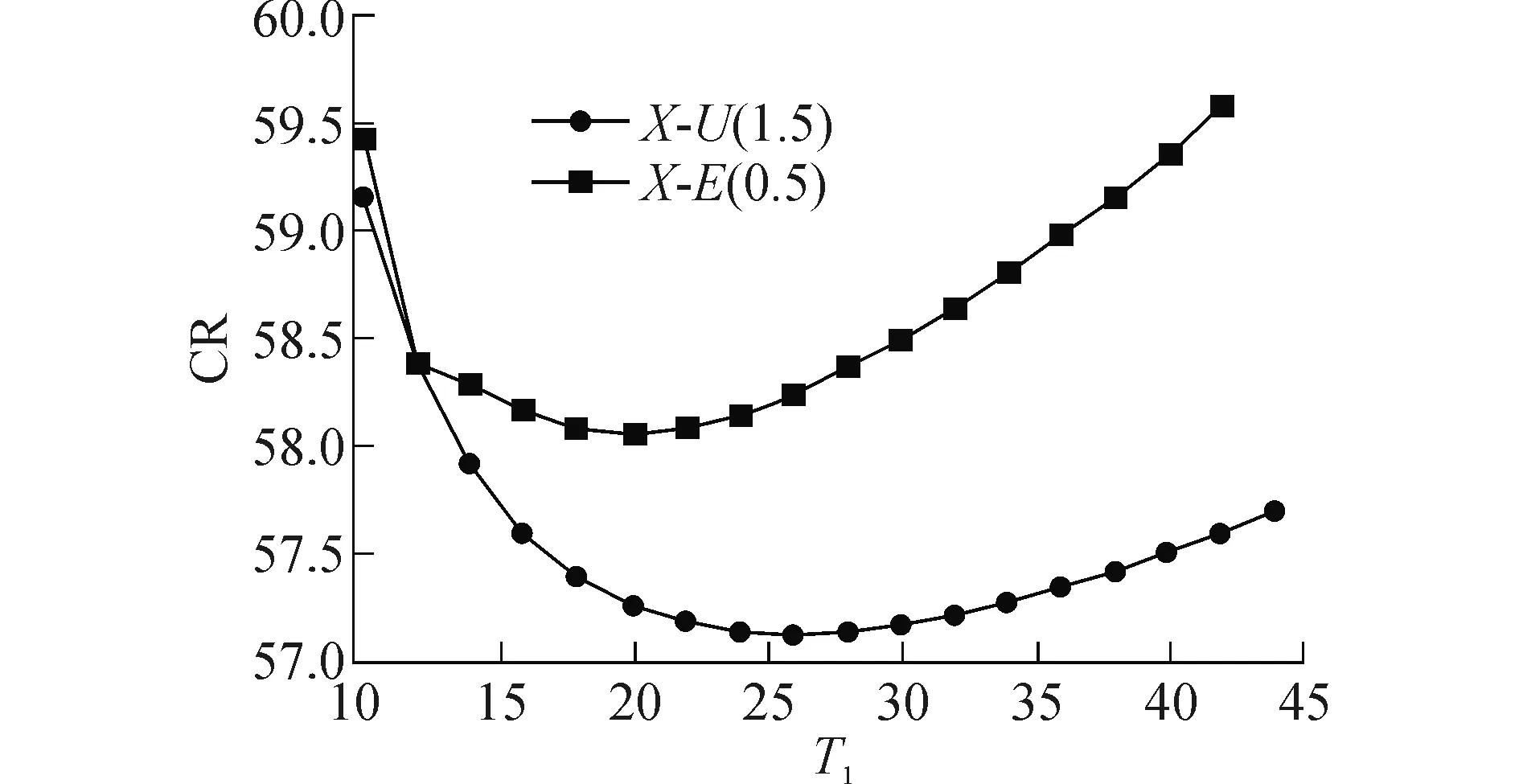
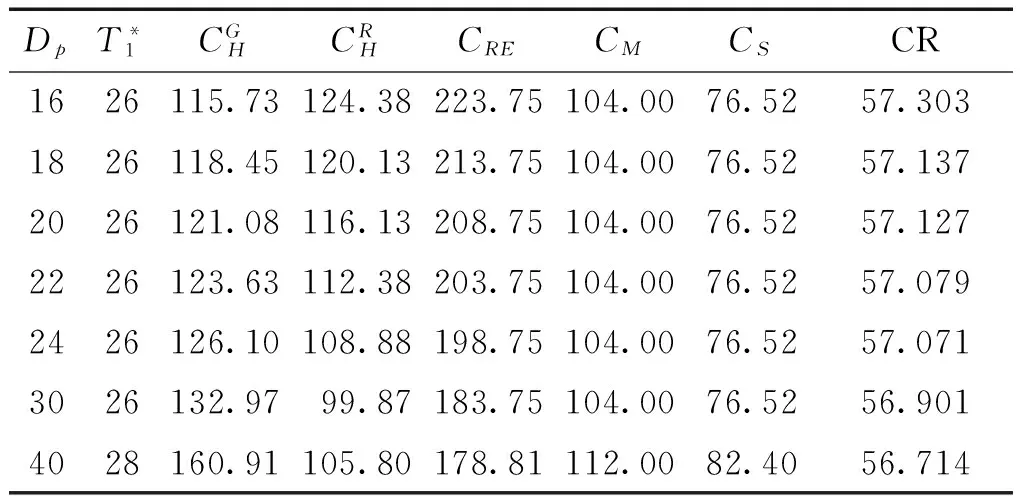
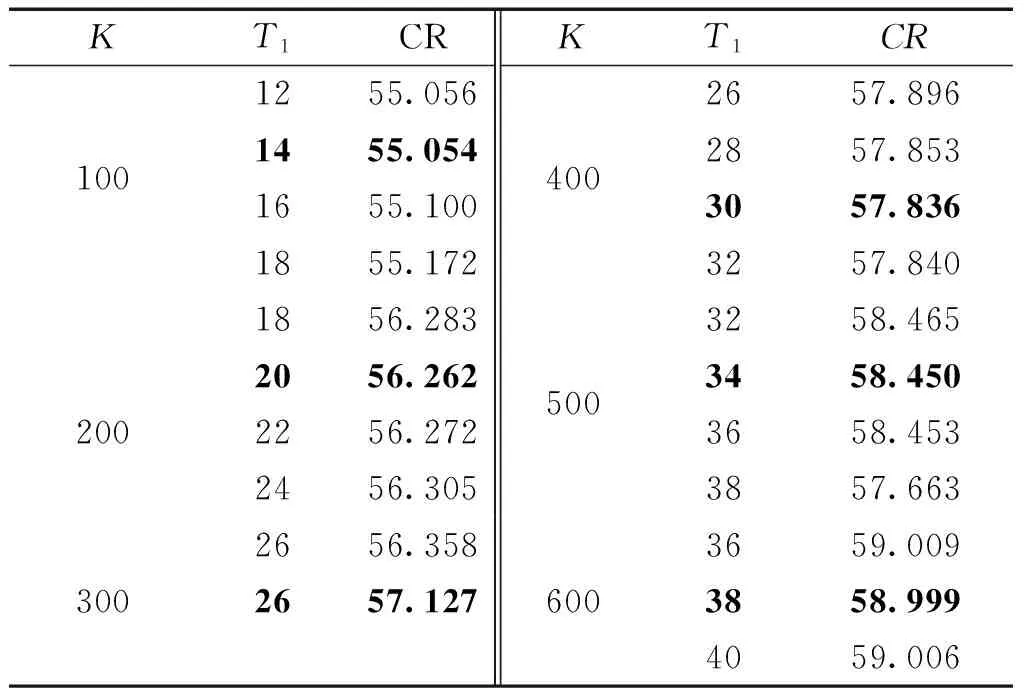
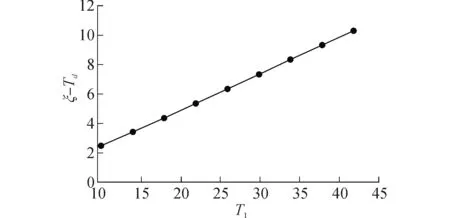
Ir21(t)=apt, 0 (16) Ir22(t)=bpt+(a-b)pτ,τ≤t≤T1 (17) 则不合格品的库存持有成本为 (18) 化简得 综合以上两种情形,合格品和缺陷品的总期望库存持有成本分别为 (19) (20) 1.3.2 其他成本 两种情形分别对应的不合格品的总数目: (21) 其期望值 (22) (23) 一个生产周期内的生产成本:CP=cppT1 (24) 随着生产单元劣化程度的增大,维护所需付出的人力物力成本也随之增大,此处假设对生产单元的预防维护成本与其劣化量成正比(CM∝X(T1)),即下列等式成立: (25) 式中:γ0为一常数,γ>0。 设ω(ξ)表示缺货时间,则 其中缓冲耗尽所需时间Td可通过下式表达 (26) φ(ξ)=λe-λξ (27) (28) 式中:γ1为一常数,γ1>0。 于是,缺货成本的期望值为 (29) 设生产准备成本为K,由式(19)~(20),(23)~(25)及(29),可以得到一个生产周期内单位产品的总成本为 (30) 本节通过一个数值实例来对所提模型进行演示,模型中各参数的设置见表1。其中,伽马过程的参数α和β采用最大似然法进行估计[16],其他参数参考实际生产中的相关数据确定。 表1 模型中的各项参数 首先,假设下游装配单元的需求速率分别服从区间[1,5]的均匀分布和参数为0.5的指数分布,分别计算这两种情形下产品的总成本率随生产周期T1的变化而发生的变化情况,如图3。 图3 产品的总成本率CR随生产周期T1的变化Fig.3 Production period versus totatl expected costs per unit 从图3可知,若下游需求服从区间[1,5]的均匀分布,则最优生产周期T1*=26,此时单位产品的总成本最小,为57.127;若下游需求服从参数为0.5的指数分布,可求得最优生产周期T1*=20,对应的最小单位产品总成本为58.05。 下面对模型中的相关参数作敏感性分析,旨在分析这些参数的变化对上述各项成本及最优生产周期所造成的影响(以X~U[1,5]为例)。 Dp的变化对T1*及各项成本的影响见表2。 表2Dp的变化对T1*及各项成本的影响 Table 2 Threshold of state transition versus optimal production period and various costs DpT*1CGHCRHCRECMCSCR1626115.73124.38223.75104.0076.5257.3031826118.45120.13213.75104.0076.5257.1372026121.08116.13208.75104.0076.5257.1272226123.63112.38203.75104.0076.5257.0792426126.10108.88198.75104.0076.5257.0713026132.9799.87183.75104.0076.5256.9014028160.91105.80178.81112.0082.4056.714 由表2可以得到以下结论: 1)最优生产周期T1*对Dp的变化并不敏感。当Dp在20上下以2个单位递减或递增时,T1*始终保持为26;当Dp增大到40时,T1*才增大为28。这表明在Dp的增幅较大时,T1*会随着Dp的增大而增大; 2)当T1*=26时,维护成本CM和缺货成本CS的值均保持不变,这是因为假设维护时间与生产单元的劣化量成正比,根据伽马过程的性质,在时刻T1,生产单元的期望劣化量E[X(T1)]=αT1,于是可以得到:维护时间与生产周期T1也成正比。同理可证:在T1不变时,缺货成本CS也是一定值。 4)对比表2中的最后两行,可以看到:Dp=40对应的不合格品库存成本大于Dp=30对应的不合格品库存成本,但前者的返工成本却小于后者。这表明前者的不合格品数实际上小于后者,而前者的不合格品库存成本较大的原因在于其对应的生产周期T1=28>26(库存成本不仅取决于库存数量,还取决于持有时间)。 Table 3 Set-up costs versus optimal production period and expected costs per unit KT1CRKT1CR1002003001255.0561455.0541655.1001855.1721856.2832056.2622256.2722456.3052656.3582657.1274005006002657.8962857.8533057.8363257.8403258.4653458.4503658.4533857.6633659.0093858.9994059.006 缺货时间随T1的变化情况如图4。 图4 缺货时间随T1的变化情况Fig.4 production period versus shortage time 图4可以看到:随着生产周期T1的增大,缺货时间逐渐增大,两者大致呈线性关系。这是因为尽管T1的增大使积累的合格品库存变大,在下游需求模式未发生改变的情况下可维持装配单元继续工作的时间越长,但是由于生产周期变长引起的维护时间的增大量更多,导致两者的差值(即缺货时间)越来越大。 1)以一个两单元一缓冲系统为研究对象,假设上游生产单元的劣化过程服从定态伽马过程,当其劣化量达到一定水平时,生产过程由“受控”转变为“失控”状态(后者的缺陷品率较大),这一假设更好地符合实际生产情形,为生产企业及时开展设备维护、产品质量控制提供了一种新的思路; 2)模型假设下游装配单元的的需求速率不恒定,为一随机变量,也很好契合了实际中客户需求难以预测这一特点。 3)在以上两条假设的基础上,以生产周期长度为决策变量,构建了最小化单位产品总成本的最优生产周期模型,并通过数值实例验证了所提模型的有效性。分析结果表明:本文优化模型对描述产品不合格率随生产设备劣化量的增大而增大、以及需求随机条件下的库存、维护等成本分析是切实有效的,对于企业合理安排生产计划、降低运行成本具有一定指导意义。 关于本文今后的研究工作有以下几个方面:假设在每一生产周期结束后对生产单元进行的预防维护只能“修复非新”,决策变量可以增加为对生产周期和生产速率的联合优化等。 [1]周炳海, 刘子龙. 考虑质量损失的退化系统维护建模[J].浙江大学学报: 工学版, 2016, 50(12): 2270-2276. ZHOU Binghai, LIU Zilong. Maintenance modelling for deteriorating system considering quality loss[J]. Journal of Zhejiang University: engineering science, 2016, 50(12): 2270-2276. [2]ZHOU B H, LIU Z L. Optimizing preventive maintenance: a deteriorating system with buffers[J]. Industrial management & data systems, 2016, 116(8): 1719-1740. [3]SANA S S. Preventive maintenance and optimal bufferinventory for products sold with warranty in an impe-rfect production system[J]. International Journal of production research, 2012, 50(23): 6763-6774. [4]CHELBI A, AIT-KADI D. Joint optimal buffer inventory and preventive maintenance strategy for a randomly failing production unit[J]. Journal of decision systems, 2003, 12(1): 21-30. [5]REZG N, DELLAGI S, CHELBI A. Joint optimal inventory control and preventive maintenance policy[J]. International Journal of Production Research, 2008, 46(19): 5349-5365. [6]成国庆, 周炳海, 李玲. 考虑缓冲区库存的退化系统最优维修更换策略[J]. 计算机集成制造系统, 2015, 21(6): 1593-1600. CHENG Guoqing, ZHOU Binghai, LI Ling. Optimal maintenance strategy for deteriorating systems with intermediate buffers[J]. Computer integrated manufacturing systems, 2015, 21(6): 1593-1600. [7]KARAMATSOUKIS C C, KYRIAKIDIS E G. Optimal maintenance of a production inventory system with-idle periods[J]. European journal of operational research, 2009, 196: 744-751. [8]PAVITSOS A, KYRIAKIDIS E G. Markov dicision models for the optimal maintenance of a production unitwith an upstream buffer[J]. Computers & Operations Research, 2009, 36: 1993-2006. [9]KARAMATSOUKIS C C, KYRIAKIDIS E G. Optimal maintenance of two stochastically deteriorating machines with an intermediate buffer[J]. European journal of operational research, 2010, 207: 297-308. [10]RADHOUI M, REZG N, CHELBI A. Joint quality control and preventive maintenance strategy for imperfect production processes[J]. Journal of intelligent manufacturing, 2010, 21(2): 205-212. [11]LIN G C, GONG D C. On a production-inventory system of deteriorating items subject to random machinebreakdowns with a fixed repair time[J]. Mathematical and computer modelling, 2006, 43: 920-932. [12]WIDYADANA G A, WEE H M. Optimal deterioratingitems production inventory models with random machine breakdown and stochastic repair time[J]. Applied mathematical modelling, 2011, 35: 3495-3508. [13]CHEN W J. Minimizing total flow time in the singlemachine scheduling problem with periodic maintenance[J]. Journal of the operational research society, 2006,57(4): 410-415. [14]ZEQUEIRA R I, BERENGUER C. Periodic imperfect preventive maintenance with two categories of competing failure modes[J]. Reliability engineering & system safety, 2006, 91(4): 460-468. [15]陶红玉, 周炳海. 基于随机退化的串行生产系统机会维护模型[J]. 上海交通大学学报, 2013, 47(12): 1911-1917. TAO Hongyu, ZHOU Binghai. Opportunistic maintenance model for series production systems based on stochastic degradations[J]. Journal of Shanghai Jiao Tong University, 2013, 47(12): 1911-1917. [16]翟子青. 基于随机过程的蒸汽发生器传热管腐蚀失效寿命分析[D]. 上海: 上海交通大学, 2011: 34-38. ZHAI Zi Qing. Stochastic modeling for the degradation of steam generator tubes due to pitting corrosion[D]. Shanghai: Shanghai Jiao Tong University, 2011:34-38. 本文引用格式: 周炳海,刘玉旺. 考虑设备劣化及随机需求的最优生产周期模型[J]. 哈尔滨工程大学学报, 2017, 38(6): 950-955. ZHOU Binghai, LIU Yuwang. An optimal production period model for a buffered system with machine deteriorating upstream and stochastic demand downstream[J]. Journal of Harbin Engineering University, 2017, 38(6): 950-955. An optimal production period model for a buffered system with machine deteriorating upstream and stochastic demand downstream ZHOU Binghai, LIU Yuwang (School of Mechanical and Energy Engineering, Tongji University, Shanghai 201804, China) During production, machine deterioration and stochastic demand can cause an increased probability of producing defective items and a shortage of WIPs, respectively. Hence, an optimal production period model considering machine deterioration upstream and stochastic demand downstream was formulated. First, a gamma process was introduced to model the degradation of the upstream machine; after the degradation state exceeded a predetermined threshold, the production state transformed from “in-control” to “out-of-control.” Based on the abovementioned descriptions, a mathematical model with an objective function for minimizing the total expected cost per unit was derived, assuming the downstream demand rate was stochastic. Finally, a numerical example was provided to illustrate the application of the proposed model, and sensitivity analysis of the model with respect to some key parameters was performed. Results show that the proposed model has certain instructive significance in quality control and for cost reduction of imperfect production systems. machine deterioration;Gamma process;stochastic demand;buffer;optimization 2016-03-23. 网络出版日期:2017-05-04. 国家自然科学基金项目(71471135). 周炳海(1965-), 男, 教授, 博士生导师. 周炳海,E-mail: bhzhou@tongji.edu.cn. 10.11990/jheu.201603079 http://www.cnki.net/kcms/detail/23.1390.u.20170504.1053.002.html TP391 A 1006-7043(2017)06-0950-06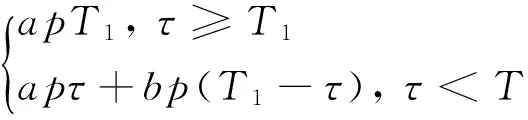
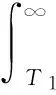
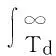
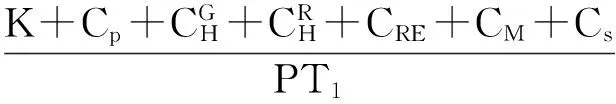
2 数值实例

3 结论
