基于波门预估递推剔除大跳动星点快速求解姿态算法研究

刘腾骏,林荣峰,朱晏庆,周 宇,肖东东

(上海航天控制技术研究所,上海 201109)



基于波门预估递推剔除大跳动星点快速求解姿态算法研究

刘腾骏,林荣峰,朱晏庆,周 宇,肖东东

(上海航天控制技术研究所,上海 201109)

考虑星敏感器对快速性、稳定性和高精度的需求，针对传统星敏感器软件在采集波门出现大跳动采集星点时而出现星跟踪失败和姿态四元数信息无法输出的缺点，对一种基于波门预估递推剔除大跳动星点快速求解姿态的方法进行了研究。根据四元数及姿态矩阵，采用基于距离的有效数据提取方法以剔除无效和跳变的星点数据；针对不同天区的不同星点运动幅度各异的特征，采用预估递推波门大小可根据不同星点确定各自的波门半径，以减少因波门半径产生的无法跟踪和波门多星识别失败现象。改进了波门参数设定，并对波门跟踪进行优化：根据算得的旋转角度与真实转过角度的差异剔除无效星点并进行更新，由更新后的旋转角和姿态四元数估计新的四元数。数学仿真结果表明：该法可有效减小星点大跳动对姿态求解的影响，提高星敏感器输出四元数姿态的精度。

星敏感器； 波门跟踪； 多矢量定姿； 估计递推算法； 星点跳动； 星点剔除； 四元数； 波门参数

0 引言

星敏感器的工作原理是通过拍摄星图、图像预处理、星点质心提取、计算观测星在星敏感器测量坐标系中的分量，实现星图特征提取、全天识别、星跟踪、姿态解算等，得到星敏感器相对惯性系的姿态四元数。国内星敏感器应用软件开发普遍基于DSP或AT697处理平台，主要完成与FPGA数据交互、星敏感器工作模式管理、功能模块实现，从而以恒星测量为基础，进行姿态确定[1]。工程实践中，星跟踪匹配成功后，在进行姿态解算时一般会采用计算量较大的多矢量确定姿态的算法求解姿态[2-3]。因矢量确定姿态求解过程存在需对中间矩阵进行代数平均求解的缺陷，故在星点跳动、毛刺、干扰时会出现姿态输出跳变，进而输入至控制系统，造成卫星姿态的抖动并降低相关载荷的工作效率和质量[4-6]。针对上述问题，国内有研究单从星敏感器姿态确定算法，分别采用q-方法、QUEST算法、ESOQ2算法、SVD算法和FOAM算法进行姿态确定求解，但由于计算均较复杂，不便于工程实现，在应对星点跳动、毛刺时会出现姿态跳动，效果并不理想[4，7-8]。后续有文献基于星敏感器采用多矢量确定姿态算法结合卡尔曼滤波算法以改进在外干扰下的姿态估计，但解决大跳动星点的效果也不理想[9-11]。为此，本文结合星敏感器星跟踪时的多矢量定姿算法的特性和工程实际采集存在误差跳动的特点，针对性地设计波门预估递推提前剔除大跳动星点环节，提出了一种星敏感器基于波门预估递推剔除大跳动星点快速求解姿态的算法。

1 理论分析

1.1 四元数及姿态矩阵

姿态四元数表示法不包括三角函数，无奇点，约束条件简单，应用广泛，尤其适于描述大角度姿态机动问题[6]。

设坐标系O-xoyozo围绕ON轴转过角δ与坐标系O-xbybzb重合，ON轴与Oxo，Oyo，Ozo轴(即Oxb，Oyb，Ozb轴)间的角分别为β1，β2，β3。则O-xbybzb系相对O-xoyozo系的姿态可由δ，β1，β2，β3完全确定，即用四元数完全确定，有

q=q0+q1i+q2j+q3k

式中：i，j，k为四元数单位矢量；q0，q1，q2，q3为四元数。q的向量形式为

式中：

(1)

此处：i=1，2，3。显然满足约束条件

(2)

其中：代表旋转的四元数中只有3个是独立的。

用三角公式

根据欧拉旋转及四元数定义，可将欧拉轴/角姿态矩阵化为四元数姿态矩阵

(3)

式中：

A12=2(q1q2+q0q3)

A13=2(q1q3-q0q2)

A21=2(q1q2-q0q3)

A23=2(q2q3+q0q1)

A31=2(q1q3+q0q2)

A32=2(q2q3-q0q1)

1.2 有效数据提取模式识别原理

有效数据提取的模式识别，实际上是剔除无效的离群点，有基于统计、距离、密度、深度、偏离等多种经典方法。本文采用算法上易于工程实现和适合嵌入式软件同时具备辨识能力的基于距离的有效数据提取的模式识别方法。

因星敏感器的有效数据是针对采集星点信息有效性进行提取，设由采集星点A∈(x1,…,xn)组成，其距离关系矩阵D∈(d11,…,dnn)已知。此处：xi为一个三维坐标系中的星点；dij为星点i与星点j的欧氏距离，且

(4)

由于是比较相邻拍间的星点的信息，姿态变化很小，因此采用比较各星点变动距离之和。

1.3 星敏感器定姿原理

首先，星敏感器成像是将远处的星点进行成像投影到星敏感器CCD平面，如图1所示。采用小孔模型，V=[V1…VN]，U=[U1…UN]分别为惯性系中星点矢量集合和相对星敏感器体坐标系中的观测单位矢量集合[6]。此处：Vi为第i个星点在惯性系中的星点坐标矢量；Ui为第i个星点在星敏感器体坐标系中的观测单位矢量。图1中：点O对应星敏感器系统的成像中心，假设星敏感器Z轴与系统光轴重合，用多矢量确定姿态方法[1]。令此时姿态矩阵为A(即此时星敏感器体坐标系相对惯性系的姿态矩阵)，则多矢量的观测方程为

U=AV

(5)

或

V=BU

(6)

此观测方程的代数解为

(7)

此时求出的B为非正交矩阵。优化后可得正交的最优矩阵

(8)

式中：I为单位矩阵。由此，可解出姿态矩阵A。

图1 星敏感器成像Fig.1 Star sensor imaging

1.4 波门跟踪原理

1.4.1 传统波门跟踪方式

波门是星敏感器中用于跟踪的一个小跟踪视窗，以快速定位所跟踪的星，从而快速计算出当前的姿态。传统的波门大小设定时直接基于某个参数，不同跟踪星点的跟踪波门相同。此设计的缺陷是不同星点在不同天区时的运动幅度不一致，可能会出现不能跟踪或单波门多星问题。

1.4.2 优化波门跟踪方式

针对不同天区的不同星点运动幅度不同的特征，本文提出一种预估递推波门大小的方法。该法可针对不同的星点确定各自的波门半径，可减少因波门半径而产生的无法跟踪和波门多星识别失败的现象，在此基础上，还对当前采集的星点进行无效数据和跳变数据剔除处理。与传统波门跟踪方式相比，本文方法的抗干扰和输出鲁棒性更强，提高了星敏感器的安全可靠性。流程如图2所示。

图2 星敏感器优化后流程Fig.2 Star sensor’s process after optimized

2 星点跟踪波门建模

2.1 经典波门参数设定

经典波门参数根据星敏感器CCD成像原理，从像面像素层面设定波门大小，所确定的波门大小随不同的相机成像参数而定，同时跟踪效果也因不同的相机成像参数而各异，易误出现跟踪波门失败。不同星点在绕某轴运动时的运动如图3所示。图3中：oE轴为旋转轴；转过角度为θ；星点A、B、C为转前的位置，星点A′、B′、C′为转后的位置，各点体坐标系中坐标分别为(xA,yA,zA)，(xB,yB,zB)，(xC,yC,zC)，(xA′,yA′,zA′)，(xB′,yB′,zB′)，(xC′,yC′,zC′)。由图3可知：其各自的运动的幅度随与旋转轴的夹角而不同，某实例如图4所示。

图3 星敏感器体坐标系中星点运动Fig.3 Star point‘s movement in star sensor’s body reference

图4 星敏感器在本体坐标系中星点运动轨迹Fig.4 Star point’s movement trace

2.2 改进波门参数设定

改进的波门可根据各自星点的位置确定更精确的波门大小。首先，确定在固定旋转角时的星点位置变化。建模星点绕z轴旋转θ，如图5所示。

图5 星点位置变化Fig.5 Star point’s position

绕oz轴转动时，星点在ox、oy轴上投影值变化较大，可得此时星点A′的x，y的范围分别为

式中：φx=arctan 2(yA/xA)。同理可推导出z的范围为[cos(ψ+θ),cos(ψ-θ)]。此处：ψ-θ>0。因此，在进入波门跟踪阶段设定波门，只需根据每拍间隔时间姿态变化最大角度θmax(在星敏感器能跟踪的情况下)，选取θmax便可设定此时的波门参数为

(9)

式中：ψ>θmax。

为进一步精确跟踪波门半径，须确定此时的旋转轴矢量方向。实际工程应用中，在进入波门跟踪时上一拍的姿态四元数信息为已知，因每拍间的运动相当小，故可用上一拍的姿态四元数中旋转轴信息作为当前的旋转轴。由图5可得

(10)

oA′=

[cos(φx+θ)sinψsin(φx+θ)sinψcosψ]

(11)

则

cos(∠AoA′)=oA·oA′=

cos(φx+θ)cosφxsin2ψ+sin(φx+θ)×

sinφxsin2ψ+cos2ψ=

cosθsin2ψ+cos2ψ

(12)

同理可推得绕任意轴旋转(如图6所示，图6中点C、D为A、A′在其旋转轴垂面下的投影点)时，夹角间满足关系

cos∠AoA′=cos∠CoDsin2∠AoE+

(13)

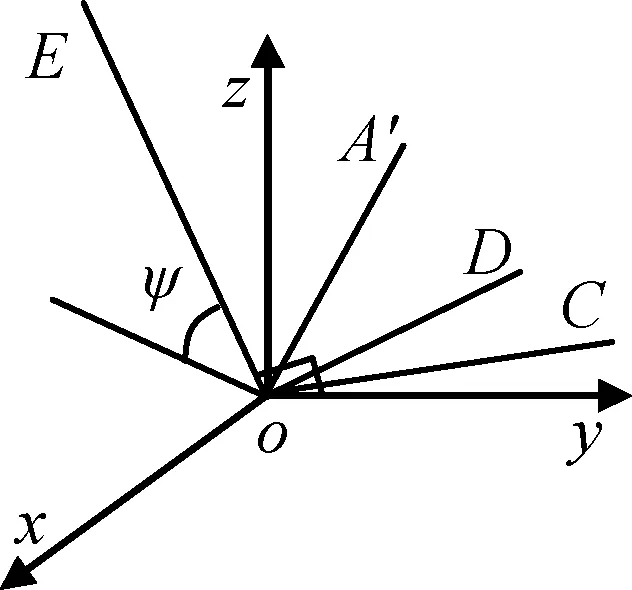
图6 星点绕任意轴旋转Fig.6 Star point’s position after rotating e vector

此时，基于波门可记录相邻拍时间的星点信息，由此可求出每个星点运动的夹角。对图3所示，运动夹角

(14)

若运动夹角在旋转轴矢量垂直平面上的夹角为真实绕四元数旋转角δ，设oA、oB、oC轴与旋转轴oE的夹角分别为ψA,ψB,ψC，则满足关系

(15)

因计算时，θA,θB,θC，ψA,ψB,ψC均已知，则可得各自的相对旋转转过的角度

(16)

将解得的δA,δB,δC代入式(9)，可得A，B，C相应波门的范围。

2.3 优化波门跟踪设计

用上述方法解得的δA,δB,δC理论上与真实转过角度δ一致。星敏感器镜头的缺陷、电路及其他噪声的影响有可能产生跳变误差较大的星点，会使δA,δB,δC与真实δ不一致，但相邻一拍间隔较短，正常情况下计算值应与真实值差异保持在一定的范围内，基于此特征，可进行星点剔除辨识。

计算中，此时的旋转轴oE采用上一拍推导出的姿态四元数计算出来的旋转轴，设上一拍的姿态四元数

(17)

旋转轴为

(18)

针对当前进入波门跟踪状态，令此时的当前跟踪星有n个，则基于优化原则剔除数据无效的点，其代价函数

(19)

因跟踪波门星点出现无效跳动数据的概率较小，考虑仅存在单一跳变数据，当Jj取最大值时，剔除此时为j的星点信息。再对剔除该星点后的旋转角度进行更新，更新后的最佳估计旋转角

(20)

(21)

式中：

(22)

3 优化波门验证

设数学仿真的基本参数为：星点矢量

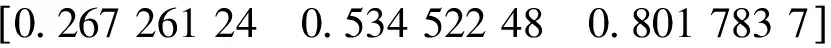
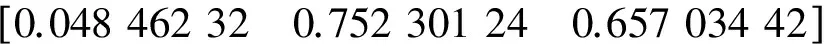
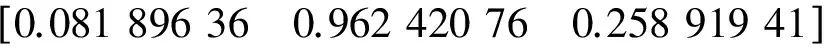
真实的旋转轴

oE=

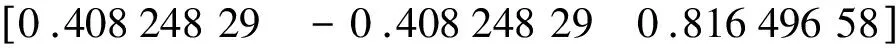
姿态机动每拍(200 ms)机动的角度0.003 rad。对机动后的oA，oB，oC的测量误差引入0.001 rad的白噪声进行干扰，仿真所得多矢量姿态与估计递推算法输出误差如图7所示。

图7 多矢量姿态与估计递推算法输出误差Fig 7 Multi vector calculating attitude comparing with predict and estimating attitude method

由图7可知：用本文波门递推预估四元数方法锁的结果不仅与真实姿态四元数误差很小，而且抖动小于传统用多矢量确定姿态的星敏感器输出，其输出曲线相对平滑。

为验证本文方法在星敏感器采集星点出现大跳动误差或错误时的有效性，引入第4个星点

oD=

[0.308 244 50 0.450 036 0 0.838 124 6]

其中针对该星点的测量时引入随机误差阈值0.01 rad的白噪声，分别用波门递推预估四元数、传统多矢量定姿、改进剔除传统多矢量定姿，以及不剔除误差大星点波门递推预估四元数4种方法进行处理，结果如图8所示。

图8 四种方法仿真结果比较Fig.8 Simulation results of four methods

由图8可知：如未剔除误差较大的星点，即使采用波门递推预估四元数方法也会出现很大的抖动，从而使星敏感器的性能下降；如采用未剔除误差较大星点，传统多矢量方法的抖动相对较大，采用波门预测剔除误差较大星点的改进多矢量方法，姿态输出抖动也很大，但优于无改进的传统多矢量方法；采用剔除误差较大星点的波门递推预估方法，抖动较小，相对真实姿态误差更小。

4 结束语

为使星敏感器在进行波门跟踪时遇到采集星点存在大跳动误差时也能快速进行星跟踪和完成姿态输出，本文给出了一种星敏感器无效星点数据优先剔除算法和基于波门有效姿态快速递推算法的解决方案。由仿真数学结果可知：该算法满足有效剔除大跳动星点，能有效削弱在进行波门跟踪时采集星点大跳动产生的对星敏感器的影响，同时改善星敏感器的输出四元数姿态的精度，可明显提高星敏感器的性能和安全可靠性。本文创新地利用波门递推进行提前剔除大跳动星点，同时结合卡尔曼滤波又进一步增加姿态输出的鲁棒性。但由于波门跟踪基于姿态递推，在快速运动时，该方法会存在星跟踪跟不上的现象，这也是本文方法的不足之处。后续，将对在快速机动下星跟踪的快速和稳定输出准备和稳定的姿态进行研究。

[1] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 2011.

[2] 朱长征. 基于星敏感器的星模式识别算法及空间飞行器姿态确定技术研究[D]. 长沙: 国防科学技术大学, 2004.

[3] 徐樱， 吴德安， 汪礼成， 等. 星敏感器慢变误差校准方法研究[J]. 上海航天， 2016， 33(4)： 63-69.

[4] 张力军. 基于多视场星敏感器的航天姿态确定方法研究[D]. 长沙: 国防科学技术大学, 2011.

[5] 姜雪原. 卫星姿态确定及敏感器误差修正的滤波算法研究[D]. 哈尔滨: 尔滨工业大学工学, 2006.

[6] 杨大明. 空间飞行器姿态控制系统[M]. 哈尔滨: 哈尔滨工业大学出版社, 2000.

[7] 谢俊峰. 卫星星敏感器定姿数据处理关键技术研究[D]. 武汉: 武汉大学, 2009.

[8] 邢飞, 董瑛, 武延鹏, 等. 星敏感器参数分析与自主校正[J]. 清华大学学报(自然科学版), 2005, 45(11):1484-1488.

[9] 林玉荣, 邓正隆. 基于星敏感器估计卫星姿态的预测Kalman滤波算法[J]. 中国科学(E辑), 2002, 32(6): 817-823.

[10] 林玉荣, 邓正隆. 基于星敏感器的星载惯性基准误差的实时估计与补偿[J]. 中国惯性技术学报, 1999(04).

[11] 李捷. 利用星敏感器的卫星姿态确定的信息滤波[J]. 中国空间科学技术, 1995, 15(2): 15-21.

A Rapid Calculating Attitude Method for Star Sensor Based on Tracing Window Using Predicting and Estimating

LIU Teng-jun, LIN Rong-feng, ZHU Yan-qing, ZHOU Yu, XIAO Dong-dong

(Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)

Taking the star sensor’s demanding for rapidity and stability and higher accuracy into consideration, a rapid calculating attitude method for star sensor based on tracing window using predicting and estimating was studied in this paper, because traditional star sensor showed star tracing failure and quaternion not being able to output while dealing with star points in tracing window having a big mistake jump. According to quaternion and attitude matrix, the extraction method of effective data was applied to reject the data of the ineffective and jumping star point based on distance. The various tracing windows related to different star points would be determined by predicting and estimating because individual star had its motion characteristic, which could reduce tracing failure caused by tracing window and multi-star identification failure. The setting of the tracing window parameters was improved. The tracing window was optimized. The ineffective star point was rejected according to the difference between the rotation angular computed and real rotational angular and the data set was updated. The new attitude quaternion was estimated by updated rotational angular and attitude quaternion. The numerical simulation results showed that this method could reduce the effect of large jumping star point on attitude determination greatly and improve the output accuracy of attitude quaternion for star sensor.

star sensor; tracing window; multi vector calculating attitude; predicting and estimating; star point jump; error star points eliminating; quaternion; tracing window parameter

1006-1630(2017)03-0116-06

2016-09-15；

2016-12-08

刘腾骏(1988—)，男，硕士，主要研究方向为卫星姿控系统软件设计与开发。

V448

A

10.19328/j.cnki.1006-1630.2017.03.016