基于谱相关函数-Wigner-Ville谱的轴承分布故障信号分析

赵发刚,王翠珍,葛 钊,周徐斌

(1.上海卫星工程研究所,上海 201109; 2.上海航天技术研究院,上海 201109)



基于谱相关函数-Wigner-Ville谱的轴承分布故障信号分析

赵发刚1,王翠珍2,葛 钊1,周徐斌1

(1.上海卫星工程研究所,上海 201109; 2.上海航天技术研究院,上海 201109)

针对包络解调技术不能有效提取滚动轴承中分布故障特征的问题，利用轴承分布故障振动信号的二阶循环平稳特性，研究了基于谱相关函数的Wigner-Ville谱的时频特征提取方法。与直接Wigner-Ville分布方法和匹配追踪时频分布方法不具备降噪功能不同，对含噪声的循环平稳信号，先用长数据序列计算得到谱相关函数，可通过计算中的多次平均显著削弱信号中噪声成分，再对谱相关函数作关于循环频率的逆傅里叶变换，得到的Wigner-Ville时频分布计算结果可有效降低噪声的干扰。对有轴承分布故障的振动信号，用滤波器去除一阶循环平稳成分，用获得的基于谱相关函数的Wigner-Ville时频谱消除平稳随机噪声的影响，能有效提取轴承分布故障的二阶循环平稳特征。仿真分析表明：所提方法能有效直观提取轴承分布故障，而普通Winger-Ville时频分布易受噪声影响，包络谱分析结果无法明确轴承分布故障特征。实验结果验证了所提时频算法提取齿轮箱轴承分布故障特征的有效性，而信号包络谱、平滑伪Wigner-Ville时频分布均无法有效提取该特征。

滚动轴承； 分布故障； 故障诊断； Wigner-Ville谱； 谱相关函数； 信号分析； 特征提取

0 引言

滚动轴承是基础关键机械零部件，据统计，约30%的旋转机械设备故障是由滚动轴承故障导致的。虽然滚动轴承的故障模式包括疲劳点蚀、表面剥落、胶合、磨损、腐蚀等多种形式，但其振动信号大致可分为局部缺陷故障信号和分布故障信号两类。目前，应用振动信号进行滚动轴承故障诊断，已能较成功监测与诊断局部缺陷故障，但对分布故障的研究较少[1-2]。这是因为在滚动轴承故障诊断中，对局部缺陷故障信号，可通过轴承的运动几何学以及包络解调技术获得故障特征频率；对分布故障信号，目前多从时域统计特征、频域能量上进行故障监测[3-4]。对齿轮箱轴承，因齿轮振动量级远大于轴承振动量级，且信号包络谱常仅反映轴承转频及其少量倍频，以及齿轮啮合频率及其少量倍频，分析结果与正常齿轮箱相差无几，因此，用现有的振动监测技术诊断齿轮箱轴承分布故障极易发生漏诊。油液分析技术是诊断轴承分布故障的一种手段，但实时性却不及振动监测技术[5-6]。文献[7]指出滚动轴承的分布故障信号具二阶循环平稳特性，文献[8]从谱相关函数角度研究了具有轴承分布故障的齿轮箱振动信号特征，其信号的谱相关函数在循环频率域以转频及其倍频表示，而在频率域则显示出轴承共振频段能量的显著升高，进而可以判断轴承分布故障的发生。

由于谱相关函数在表述轴承分布故障时缺乏直观性，本文对一种用信号的时频表示分析轴承分布故障特征的方法进行了研究。Wigner-Ville分布(WVD)是最有代表性的双线性时频分布，具时频分辨率高的优点，LOUGHLIN曾用平滑WVD分析了机械振动信号的时频特征[9]。但WVD的缺点是其易受噪声等影响。为此，本文根据谱相关函数与WVD间的关系，利用由谱相关函数得到的信号的WVD表示，在时频域提取轴承分布故障特征，并用仿真与实验分析了该方法降低噪声成分干扰，同时直观清晰地反映轴承分布故障特征的有效性[10-12]。

1 基于谱相关函数的Wigner-Ville谱的时频分析方法

定义实信号s(t)的Wigner-Ville分布为

(1)

式中：x(t)为s(t)的解析形式；符号“*”表示共轭；τ为时延；f为频率。

Wigner-Ville谱是WVD的数学期望，用于分析非平稳随机信号的时频特征，有

Wx(t,f)=

(2)

式中：E{·}为数学期望；Rx(t,τ)为时变自相关函数[13]。对循环平稳随机信号，Rx(t,τ)可写成傅里叶级数的形式

(3)

式中：Rx(τ,α)为循环自相关函数；α为循环频率，满足α=m/T1，m/T2，m/T3，…。此处：T1,T2,T3,…为Rx(t,τ)的所有周期成分；m为某一整数。Rx(τ,α)可用Rx(t,τ)表示为

(4)

对Rx(τ,α)作关于时延τ的傅里叶变换，可得谱相关函数

(5)

由式(5)可知：当α为零时，其表示平稳信号自相关函数与功率谱密度函数的关系；当α不为零时，其表征具循环平稳特性的信号特征。

联合式(2)～(5)，谱相关函数与Wigner-Ville谱关于α构成傅里叶变换对

(6)

用谱相关函数计算Wigner-Ville时频谱虽增加了一步间接的谱相关函数计算过程，但因为谱相关函数计算只需顺序计算不同频率间互相关，其实际计算时间不会大量增加，而且可有效利用长时间序列计算时频分布。

由式(4)、(5)，针对特定的α，Sx(α,f)可通过计算两个x(t)的频移信号的互功率谱密度函数得到，则有

(7)

式中：u(t)=x(t)e-jπαt;v(t)=x(t)ejπαt；Ruv(τ)为u(t)，v(t)的互相关函数。因此，计算Sx(α,f)只需通过对感兴趣的循环频率集进行扫描计算即可，而每步扫描只用式(7)，由FFT算法计算特定α下两个频移信号u(t)，v(t)的互功率谱密度即可。与直接Wigner-Ville时频分布算法相比，这可有效利用长时间序列对平稳噪声进行平均，同时由非零循环频率域信息获得具循环平稳特性的信号特征。

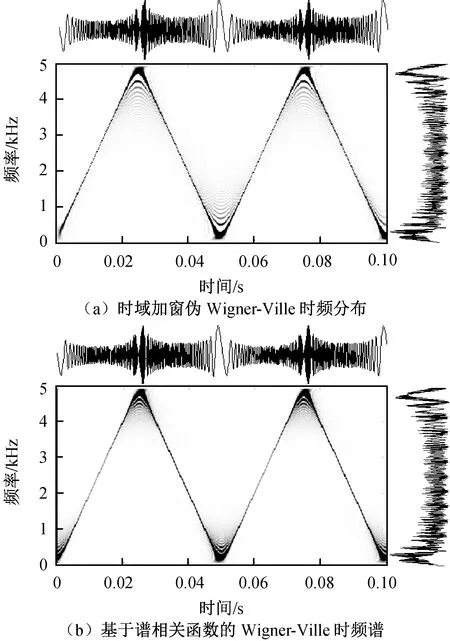
图1 周期时变系统输出信号s1(t)的时频分布Fig.1 Time frequency representations of output signal s1(t) from a periodic time varying system

现考虑无噪声影响的周期时变系统，s1(t)=2a(t)s1(t-1)-s1(t-2)，系数a(t)=cos(2πfat)。设定采样频率fs=10kHz，系统频率fa=20 Hz，令仿真输出信号幅值单位为电压V。系统输出s1(t)的时频分布如图1所示。计算时，均选择s1(t)约2个周期0.1 s的1 024点数据进行计算，图1 (b)的循环频率计算范围为[-5 000 ～5 000] Hz，每隔10 Hz用式(7)计算一次谱相关函数。

在对应图1系统输出受噪声影响时，令s2(t)=s1(t)+n(t)，此处n(t)为零均值高斯白噪声。设信噪比(SNR)为10lg((σs)2/(σn)2)=-8，此处(σs)2，(σn)2分别为s1(t)，n(t)的方差。系统输出s2(t)的时频分布如图2所示。由图2(a)可知：由于噪声的干扰，时域加窗伪Wigner-Ville时频分布无法给出有用信息；图2(b)虽受噪声影响，系统输出的周期时变特性仍清晰可见。在计算图2(b)时，选取10 s数据进行谱相关函数计算，由于采用FFT算法，数据长度的增加并未显著增加计算量。

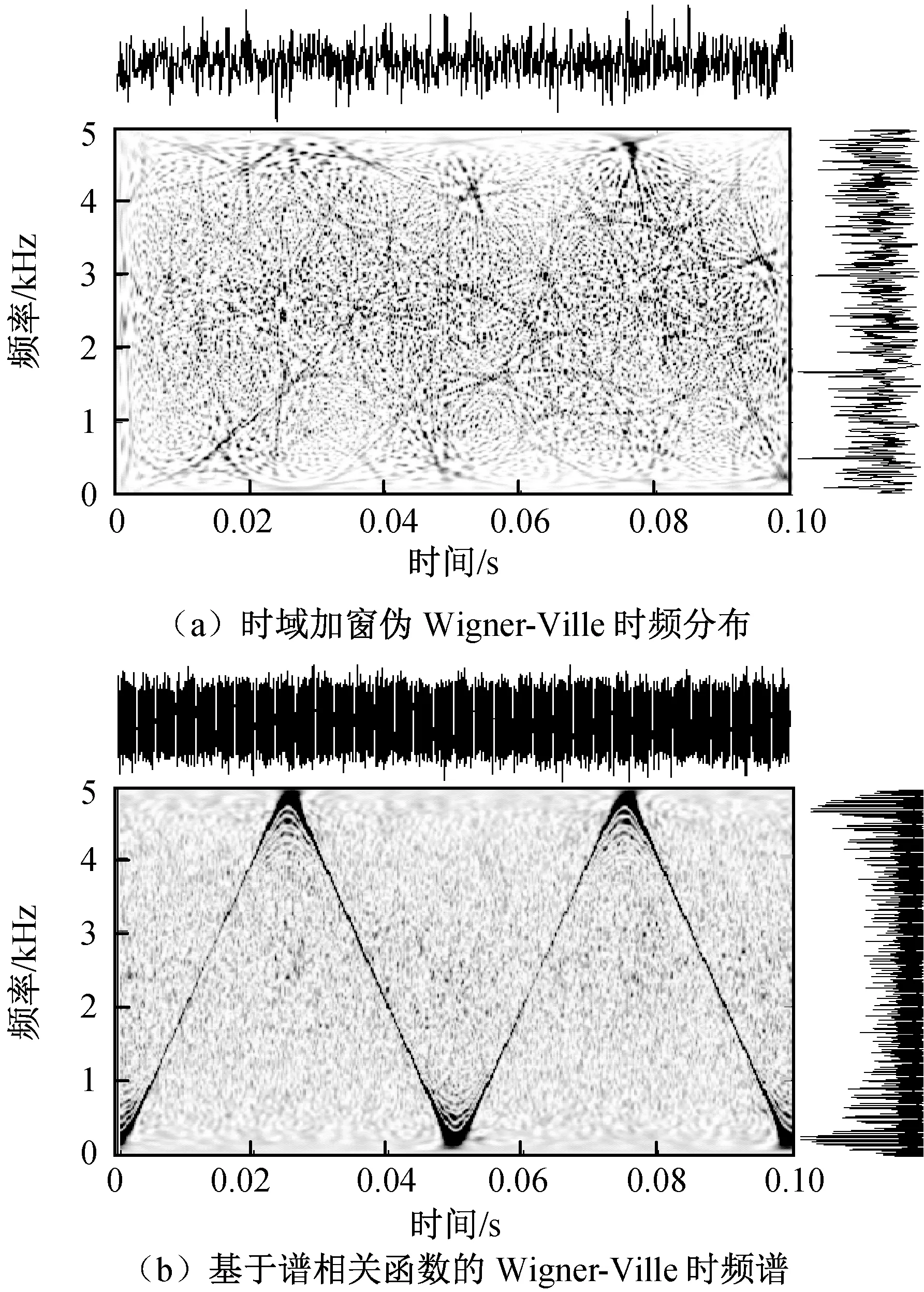
图2 受噪声影响的周期时变系统输出信号s2(t)的时频分布Fig.2 Time frequency representations of output signal s2(t) from a periodic time varying system with noise

根据图1、2分析结果可知：基于谱相关函数的Wigner-Ville时频谱可有效抑制平稳噪声的干扰，分析输出信号s1(t)，s2(t)的谱相关函数，结果如图3所示。比较图3 (a)、(b)可知：噪声的存在仅使信号谱相关函数在零循环频率处幅值明显增大，但并未破坏其非零循环频率的分布结构，因此可有效提取具有循环平稳特性的信号特征。

图3 周期时变系统输出信号s1(t)，s2(t)的谱相关函数Fig.3 Spectral correlation functions of output signals s1(t) and s2(t) from a periodic time varying system without and with noise

2 有轴承分布故障的振动信号模型

当滚动轴承出现局部缺陷故障时，其振动信号由一系列的冲击脉冲串组成。通过轴承的运动几何学，以及在轴承或加速度传感器共振频率频段的包络解调技术可有效判断轴承局部缺陷故障的发生及其位置[1]。

当轴承表面发生磨损或由于局部缺陷故障的扩展，轴承会在产生分布故障时，因滚动体与故障表面的运动接触产生的振动信号不再有明显的冲击形式，不会形成局部缺陷故障振动信号呈现具一定规律的冲击脉冲串形式。此时形成的轴承振动信号较复杂，取决于故障表面的粗糙度和分布故障面积，可能同时会有数个相邻的滚动体进入故障区域，故轴承分布故障振动信号总体表现出随机性。

但由于轴承滚动体间不是独立的，而是按一定的通过频率经过故障区域，振动信号中隐含一定的周期性，可将其视为以轴承故障部位的通过频率及其倍频为隐含周期的二阶循环平稳信号[1，7]。如故障位于轴承内圈表面，随轴承内圈与转轴旋转，故障区域还会以旋转频率为频率进入载荷区，此时轴承受到轴的支撑反力如图4所示。

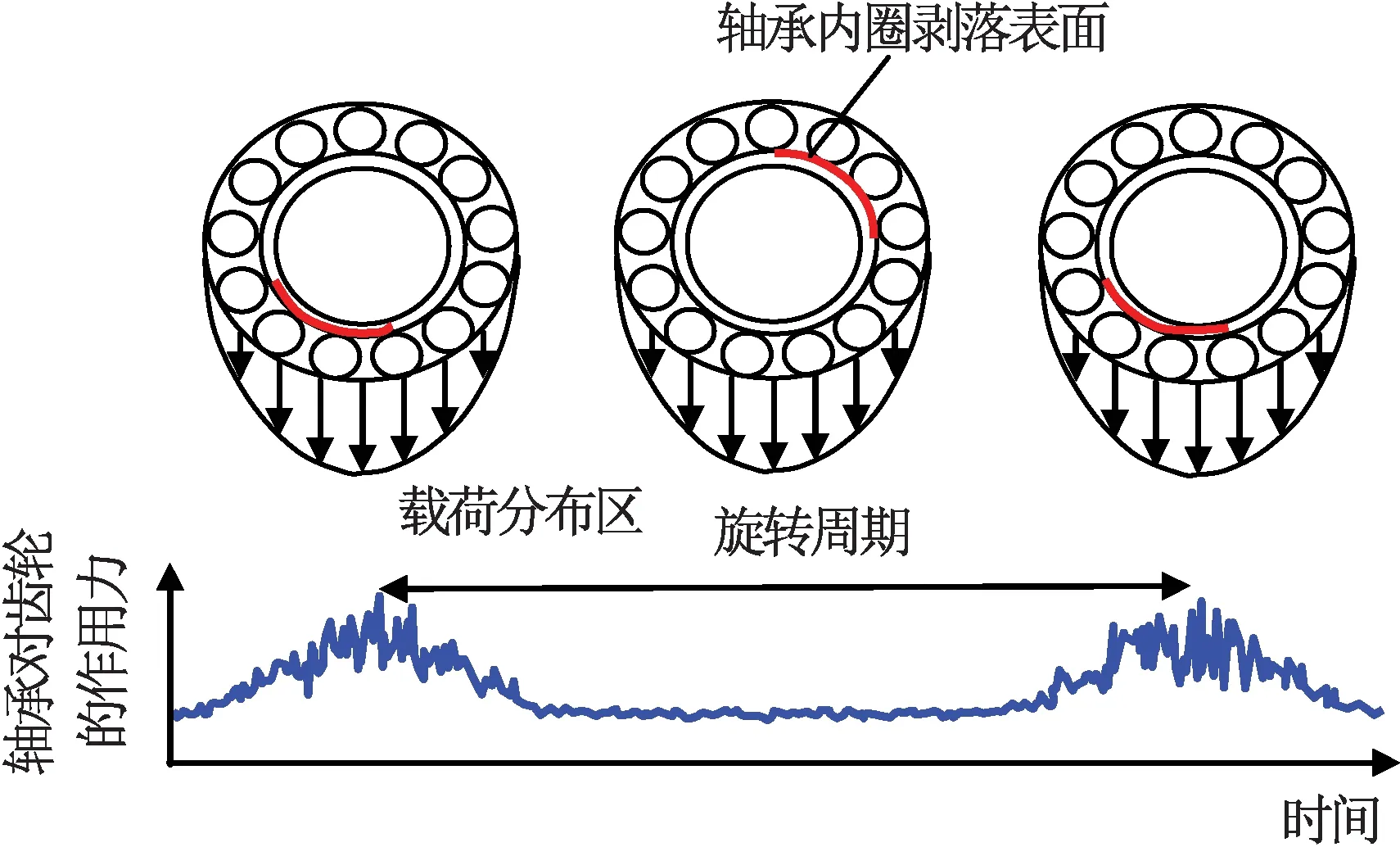
图4 轴承分布故障[1]Fig.4 Illustration of distributed bearing fault[1]

当轴承正常工作时，齿轮箱振动信号通过等角度采样消除转速波动影响后，常由频率为齿轮啮合频率和少量倍频的谐波信号构成，有

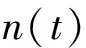
(8)

式中：am(t)，φm(t)分别为齿轮箱振动时可能产生的以齿轮轴转频及倍频为周期的幅值调制和频率调制信号；fz为齿轮啮合频率；n(t)为平稳随机噪声。式(8)表示的齿轮箱振动信号具一阶循环平稳特性[7]。

如图2所示，当滚动轴承内圈产生分布故障时，故障部位进入承载区域后，必会引起齿轮支撑力的改变，从而引起齿轮箱振动信号的幅值调制现象。此时，齿轮箱振动的信号模型可表示为

cos[2πmfzt+φm(t)]+n(t)

(9)

式中：bm(t)为由轴承分布故障引起的齿轮支撑力改变而产生的齿轮振动调制信号，其在分布故障通过承载区域时为一随机信号，而在分布故障离开承载区域时则近似为零。因此，bm(t)是隐含周期性的二阶循环平稳随机信号[7]。

由式(9)，齿轮箱振动信号包含三部分：式(8)代表的一阶循环平稳信号、轴承分布故障引起的二阶循环平稳信号，以及平稳随机噪声n(t)。相对于二阶循环平稳分量，一阶循环平稳信号所占的能量比重较大，若直接对式(9)代表的信号进行时频分析，轴承分布故障引起的二阶循环平稳振动特征就会被掩盖。为此，可先用维纳滤波器或AR滤波器设计自适应离散谱线消除滤波器，去除式(9)中的一阶循环平稳成分，然后利用基于谱相关函数的Wigner-Ville时频谱消除平稳随机噪声的影响，并有效提取轴承分布故障的二阶循环平稳特征[1，14-15]。这部分处理过程已相对成熟。

3 具有轴承分布故障的振动信号仿真分析

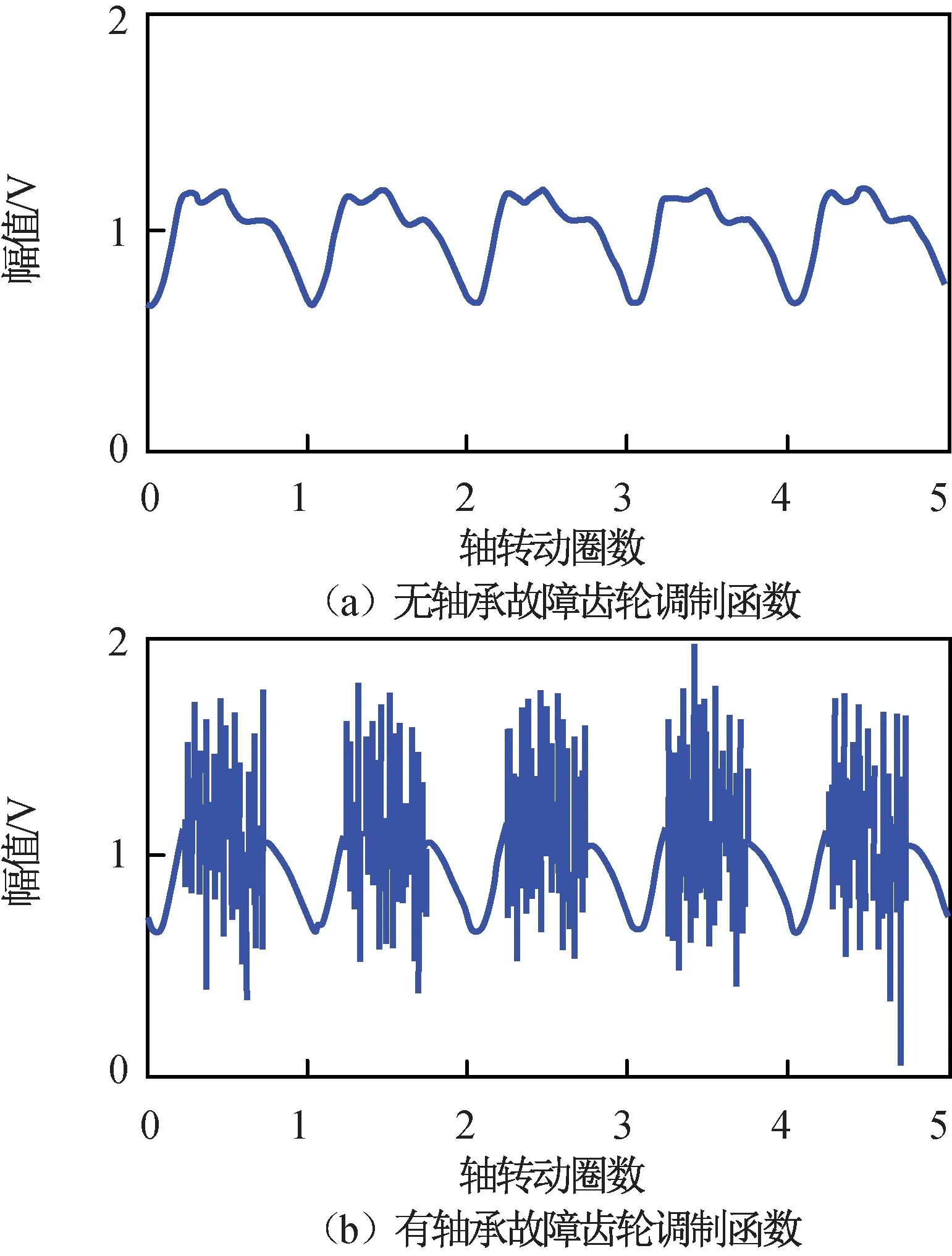
图5 无和有轴承故障的齿轮调制函数Fig.5 Gear modulation function without and with bearing fault

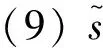
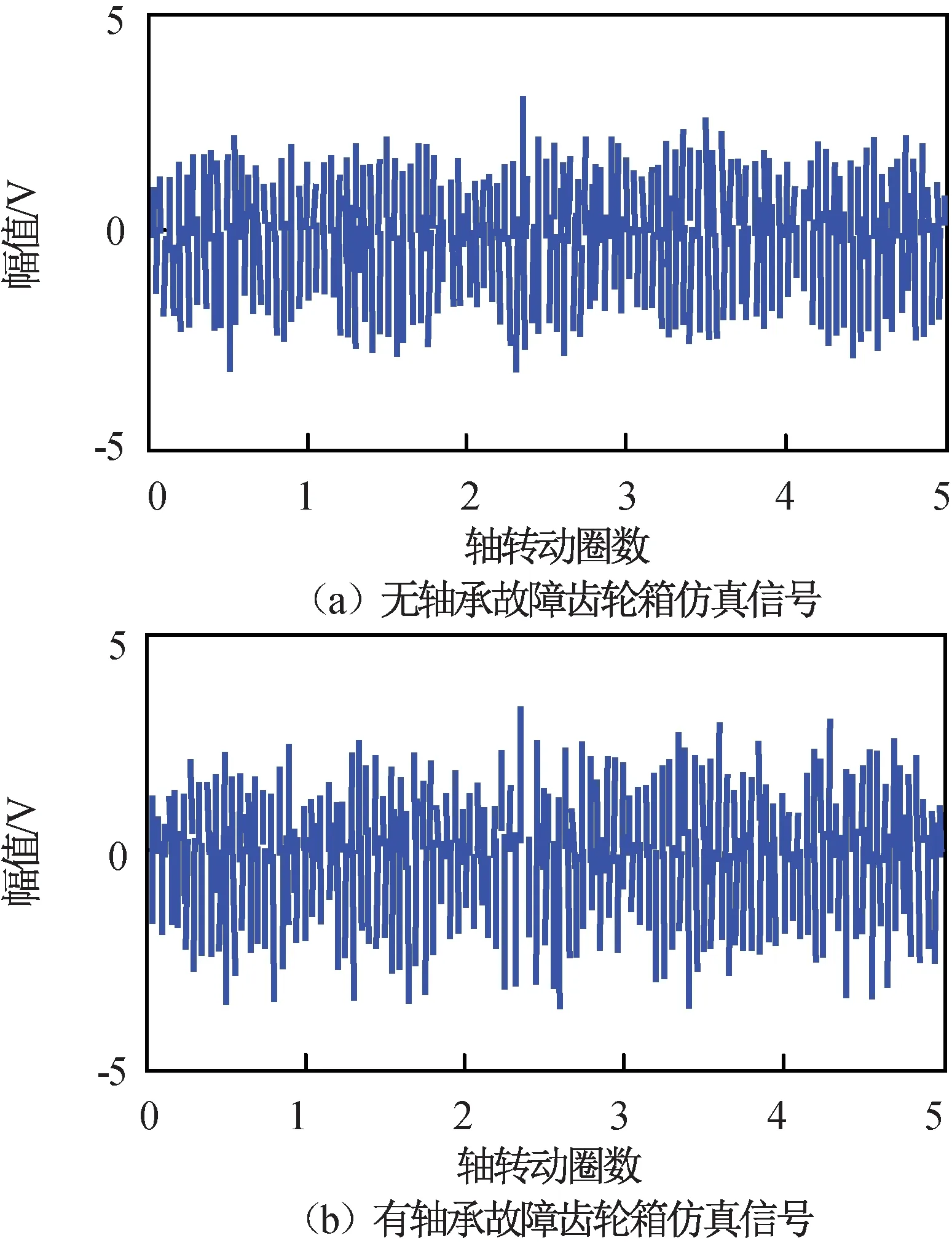
图6 无和有轴承故障的齿轮箱仿真信号Fig.6 Gearbox simulation signal without and with bearing fault

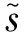
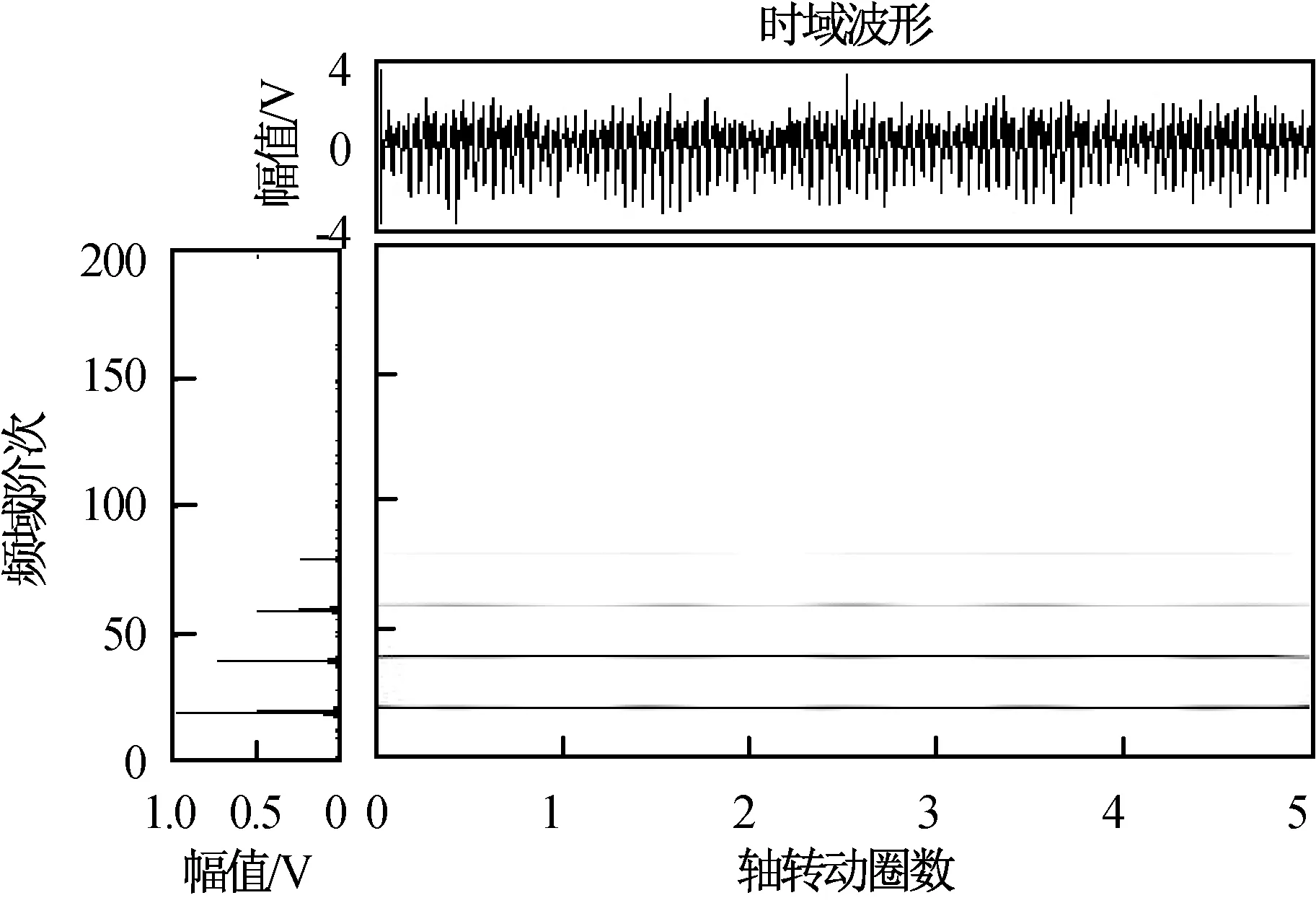
图7 自适应滤波前齿轮箱仿真信号的平滑伪Wigner-Ville时频分布Fig.7 Gearbox simulation signal before adaptive filtering-pseudo Wigner-Ville spectrum

轴转频阶次1及其倍频，齿轮啮合频率阶次20、倍频以及转频调制边频。

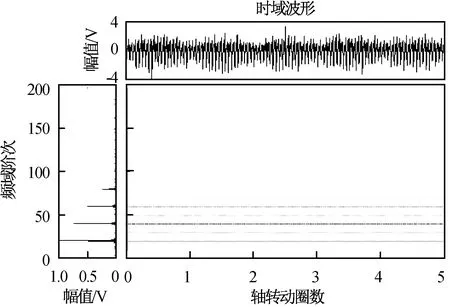
图8 自适应滤波前齿轮箱仿真信号的基于谱相关函数的Wigner-Ville时频谱Fig.8 Gearbox simulation signal before adaptive filtering-Wigner-Ville spectrum based on spectral correlation function

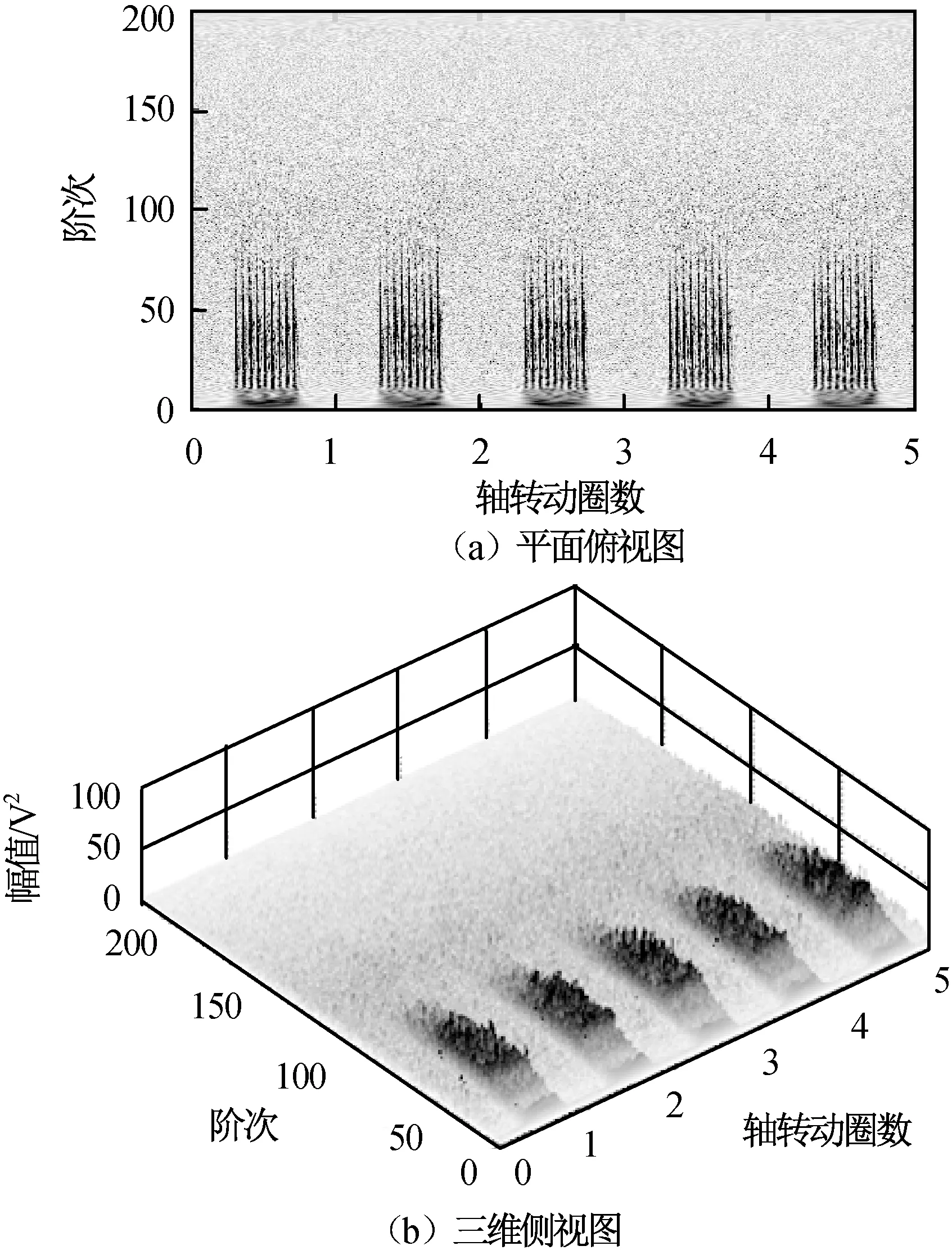
图9 自适应滤波后齿轮箱仿真信号的基于谱相关函数的Wigner-Ville时频谱Fig.9 Gearbox simulation signal after adaptive filtering-Wigner-Ville spectrum based on spectral correlation function

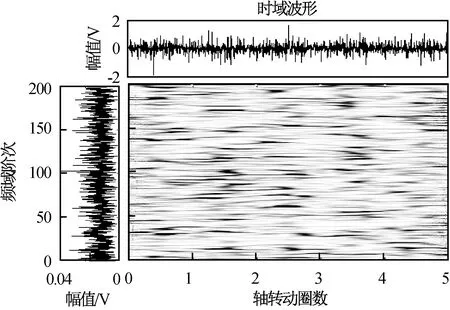
图10 自适应滤波后齿轮箱振动信号的平滑伪Wigner-Ville时频分布Fig.10 Gearbox simulation signal after adaptive filtering-pseudo Wigner-Ville spectrum

图11 自适应滤波前后齿轮箱仿真信号包络谱Fig.11 Gearbox simulation signal before and after adaptive filtering-comparison of envelope spectrum

图12 齿轮箱实验实物Fig.12 Experimental gearbox photo

比较图9～11可知：基于谱相关函数的Wigner-Ville时频谱可有效直观地提取轴承分布故障，而普通Wigner-Ville时频分布易受噪声的影响，包络谱分析结果也无法明确指示轴承分布故障特征。

4 具有轴承分布故障的齿轮箱振动信号实验分析

本文用澳大利亚新南威尔士大学的齿轮箱振动实验信号进行了实验验证[8]。该齿轮箱由一对平行轴和一对齿数比为32∶49的直齿轮组成，如图12(a)所示。其中：轴承为Koyo 1250双列自调心轴承，轴承故障为内圈磨损故障，如图12(b)所示。故障轴承位于齿轮箱驱动轴一侧，对应齿轮齿数为32。根据轴承运动学分析，其内圈通过频率为齿轮轴转速的7.1倍，外圈通过频率为齿轮轴转速的4.9倍。齿轮箱振动信号由位于故障轴承上方的加速度传感器测得，并通过齿轮轴键相信号对其进行重采样。

为消除一阶循环平稳分量的影响，对齿轮箱实验信号进行了与仿真分析相同的自适应离散谱线消除滤波。自适应滤波前后的齿轮箱实验信号包络谱如图13所示。由图13(a)可知，在自适应滤波前包络谱包含齿轮轴转频阶次1以及齿轮啮合频率阶次32；由图13(b)可知，经自适应滤波后的信号包络谱仅包含齿轮轴转频阶次。由图11包络谱分析结果不能发现任何轴承故障特征。

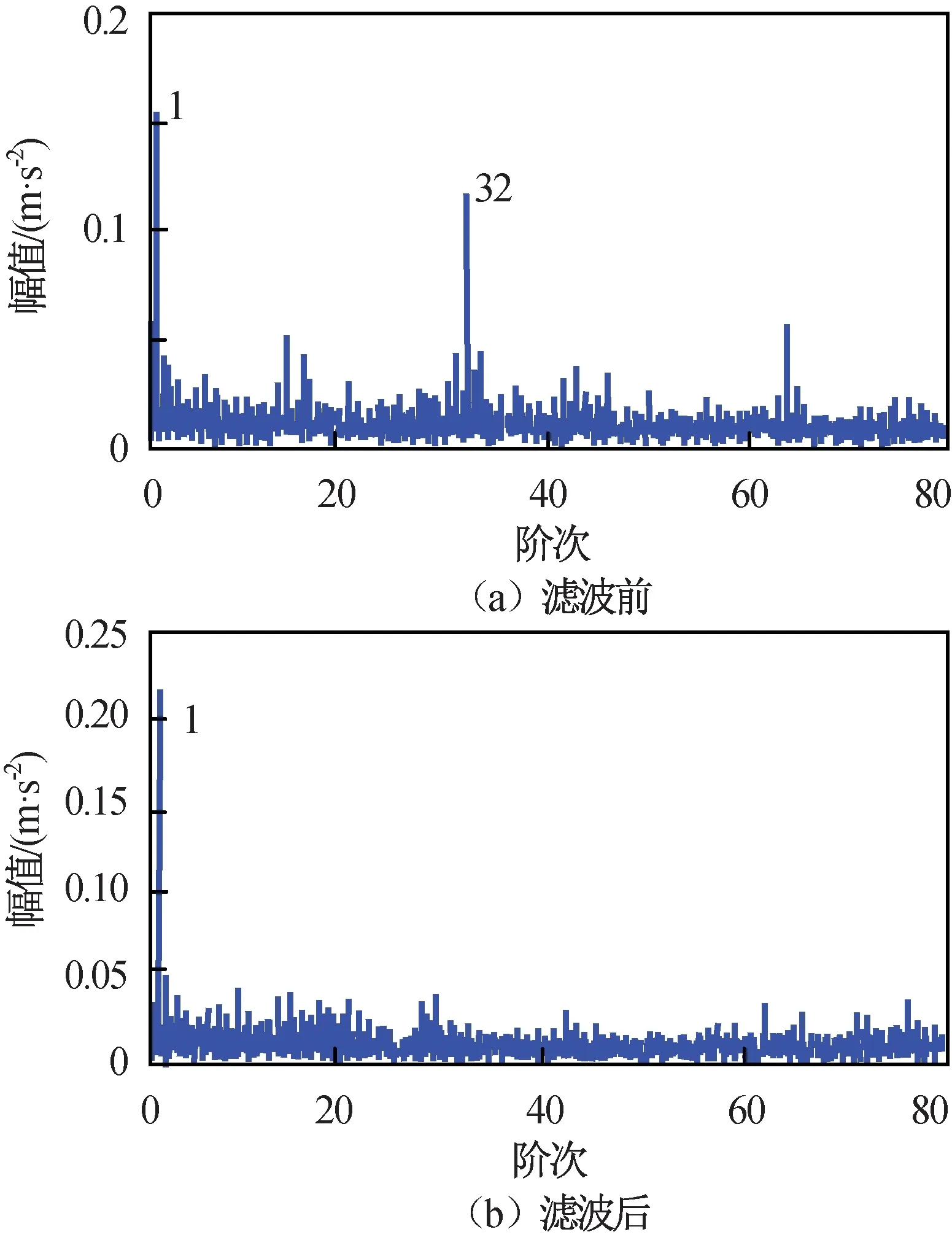
图13 自适应滤波前后-齿轮箱实验信号包络谱Fig.13 Envelope spectrum of gearbox experimental signal before and after adaptive filtering

自适应滤波前后，齿轮箱实验信号的基于谱相关函数的Wigner-Ville时频谱分别如图14、15所示。自适应滤波前，由图14可知：沿频率轴主要包含间隔为齿轮啮合频率阶次32的平行谱线，齿轮啮合频率掩盖了轴承故障特征。自适应滤波后，由图15可知：随着齿轮轴的转动，轴承分布故障特征在固定相位处周而复始，说明基于谱相关函数的Wigner-Ville时频谱有效提取了齿轮箱中的轴承分布故障特征。

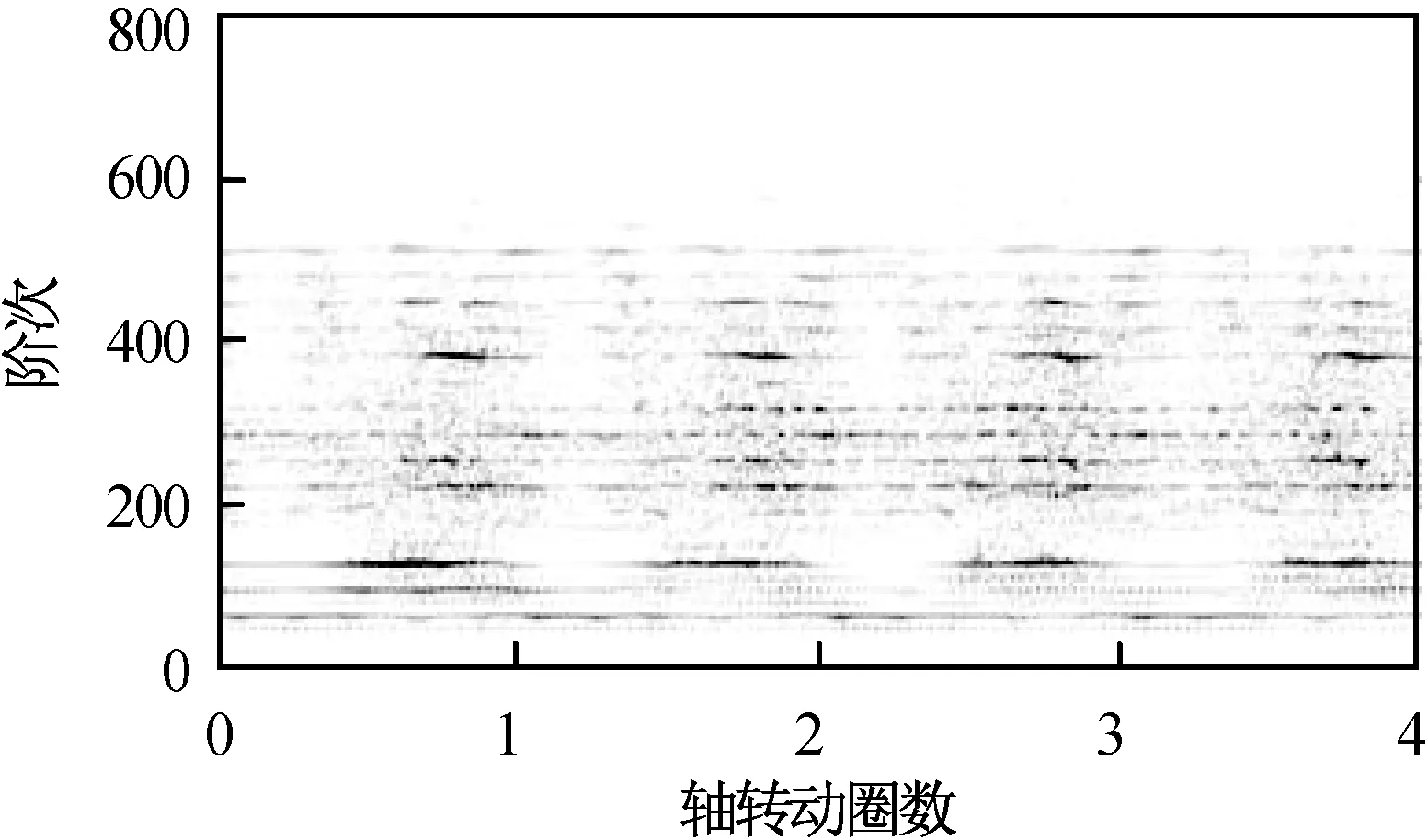
图14 自适应滤波前齿轮箱实验信号的基于谱相关函数的Wigner-Ville时频谱Fig.14 Gearbox experimental signal before adaptive filtering-Wigner-Ville spectrum based on spectral correlation function

图15 自适应滤波后齿轮箱实验信号的基于谱相关函数的Wigner-Ville时频谱Fig.15 Gearbox experimental signal after adaptive filtering-Wigner-Ville spectrum based on spectral correlation function

5 结论

本文对基于谱相关函数-Wigner-Ville谱的轴承分布故障信号分析进行了研究。利用由谱相关函数得到的Wigner-Ville谱，在时频域提取了齿轮箱中的轴承分布故障特征，仿真与实验分析表明了该方法的正确性与有效性。由于滚动轴承分布故障信号具有二阶循环平稳特性，即经过自适应离散谱线消除，去除一阶循环平稳成分后的谱相关函数在非零循环频率处仍具有非零成分，可利用基于谱相关函数在非零循环频率处仍具有非零成分来构造Wigner-Ville时频谱。本文研究的基于谱相关函数的Wigner-Ville时频谱分析特点是：可有效抑制随机噪声的影响；可有效利用长时间序列进行时频分析，能抑制随机干扰的影响；在时频域可有效提取齿轮箱中的轴承分布故障特征。本文提出的方法能有效在时频域提取轴承分布故障特征，也可有效提取噪声淹没下的轴承点蚀故障信号的时频特征[16]。相对包络谱方法可有效提取轴承点蚀故障特征，但不能有效提取轴承分布故障特征，本文提出的方法在分析轴承分布故障特征方面更有实际工程应用价值。后续研究将集中在实际工程信号，分析实际信号噪声及干扰成分对分析结果的影响。

[1] RANDALL R B, ANTONI J. Rolling element bearing diagnostics—a tutorial[J]. Mechanical Systems and Signal Processing, 2011, 25(2): 485-520.

[2] 毕果, 陈进, 李富才, 等. 谱相关密度分析在轴承点蚀故障诊断中的研究[J]. 振动工程学报, 2006, 19(3): 388-393.

[3] 程辉, 朱昆泉. 滚动轴承磨损故障的诊断[J]. 轴承, 1989(5): 51-56.

[4] BARTELMUS W, CHAARI F, ZIMROZ R, et al. Modelling of gearbox dynamics under time-varying nonstationary load for distributed fault detection and diagnosis[J]. European Journal of Mechanics—A/Solids, 2010, 29(4): 637-646.

[5] HALME J, ANDERSSON P. Rolling contact fatigue and wear fundamentals for rolling bearing diagnostics—state of the art[J]. Proceedings of the Institution of Mechanical Engineers Part J—Journal of Engineering Tribology, 2010, 224(J4): 377-393.

[6] 陈果, 陈立波, 宋兰琪. 一种磨损故障融合诊断新方法及其应用[J]. 机械科学与技术, 2009, 28(9): 1157-1161.

[7] ANTONI J, RANDALL R B. Differential diagnosis of gear and bearing faults[J]. Journal of Vibration and Acoustics—Transactions of the ASME, 2002, 124(2): 165-171.

[8] SAWALHI N, RANDALL R B. Simulating gear and bearing interactions in the presence of faults—part II: simulation of the vibrations produced by extended bearing faults[J]. Mechanical Systems and Signal Processing, 2008, 22(8): 1952-1966.

[9] LOUGHLIN P, BERNARD G. Cohen-posch (positive) time-frequency distributions and their application to machine vibration analysis[J]. Mechanical Systems and Signal Processing, 1997, 11(4): 561-576.

[10] GARDNER W A. Introduction to random processes with applications to signals and systems: chapter 12 cyclostationary processes[M]. New York: McGraw-Hill Inc, 1990.

[11] GIANNAKIS G B. Digital signal processing handbook: chapter 17 cyclostationary signal analysis[M]. New York: CRC Press & IEEE Press, 1998.

[12] ANTONI J. Cyclic spectral analysis in practice[J]. Mechanical Systems and Signal Processing, 2007, 21(2): 597-630.

[13] 王宏禹. 非平稳随机信号分析与处理[M]. 北京: 国防工业出版社, 1999.

[14] ANTONI J, RANDALL R B. Unsupervised noise cancellation for vibration signals: part I—evaluation of adaptive algorithms[J]. Mechanical Systems and Signal Processing, 2004, 18(1): 89-101.

[15] ANTONI J, RANDALL R B. Unsupervised noise cancellation for vibration signals: part II—a novel frequency-domain algorithm[J]. Mechanical Systems and Signal Processing, 2004, 18(1): 103-117.

[16] ZHOU Y, CHEN J, DONG G M, et al. Wigner-Ville distribution based on cyclic spectral density and the application in rolling element bearings diagnosis[J]. Proceedings of the Institution of Mechanical Engineers Part C—Journal of Mechanical Engineering Science, 2011, 225(C12): 2831-2847.

Spectral Correlation Function-Wigner-Ville Spectrum based Signal Analysis of Bearing Distributed Fault

ZHAO Fa-gang1, WANG Cui-zhen2, GE Zhao1, ZHOU Xu-bin1

(1. Shanghai Institute of Satellite Engineering, Shanghai 201109, China; 2. Shanghai Academy of Spaceflight Technology, Shanghai 201109, China)

To solve the problem that the features of distributed faults of rolling element bearings in gearboxes can not be effectively extracted by envelop demodulation techniques, based on the second order cycle stationary characteristics of vibration signals of bearings with distributed faults, the time frequency feature extraction method of Wigner-Ville spectrum based on spectral correlation function was studied in this paper. Different from the general time frequency representation methods of direct Wigner-Ville spectrum and matching tracking spectrum, the spectrum correlation function was obtained by long data serials computation for cycle stationary signal, in which the noise in the signal could be decreased by the multiply average. Then the Winger-Ville spectrum gained by inverse Fourier transform for cycle frequency, which had reduced the noise disturbance effectively. For the vibration signal of bearing with distributed fault, the first order cycle stationary was filtered by the filter. The effect of stationary random noise was eliminated by the spectral correlation function-Wigner-Ville spectrum obtained. So the features of the second order cycle stationary for the bearing with the distributed fault could be extracted effectively. The simulation results show that the method proposed can extract the distributed fault of bearing but the common Wigner-Ville spectrum method cannot, because the latter is easy to be affected by the noise so that the envelope spectrum analysis cannot obtain the features of the distributed fault. The experiment proves the method proposed is effective in the analysis of gearboxes with bearing distributed faults but the methods of signal envelope spectrum and smooth pseudo Wigner-Ville spectrum are not.

rolling bearing; distributed fault; fault diagnosis; Wigner-Ville spectrum; spectral correlation function; signal analysis; feature extraction

1006-1630(2017)03-0122-09

2017-04-16；

2017-05-10

国家自然基金资助(51505294)

赵发刚(1981—)，男，博士，高级工程师，主要从事卫星的结构机构设计、振动测试与信号分析。

TH133.33

A

10.19328/j.cnki.1006-1630.2017.03.017