一类Diophantine方程在实二次Euclid域上的整数解

赵西卿,董晓明,张 昕,杨 芝,洪 霞,王伟伟

(延安大学 数学与计算机科学学院, 陕西 延安 716000)



一类Diophantine方程在实二次Euclid域上的整数解

赵西卿,董晓明,张 昕,杨 芝,洪 霞,王伟伟

(延安大学 数学与计算机科学学院, 陕西 延安 716000)

研究了一类典型的Diophantine方程在实二次Euclid域中的整数解问题。主要利用二次域中的理论和二次代数整数环中算术基本定理,证明了此类Diophantine方程在特殊情形下无整数解的相关结论。

Diophantine方程; 实二次域; 整数解

1 预备知识

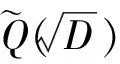
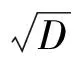
引理2[10]设D满足引理1的条件,即

那么, α是二次代数整数的充要条件,可表示为

α=m+nω,m,n∈Z,n≠0

(1)

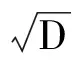
2 定理及证明

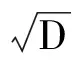
x2-D=4y5

(2)

均无整数解。

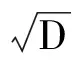
(3)

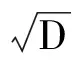
(4)

即

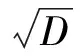
故有

(5)

由式(5)可得b=±1或±2k,其中k=1,2,3,4。

③ 若b=±2k时,右边b(5a4+10Da2b2+D2b4)≡0(mod25),左边24≡24(mod25),矛盾。从而Diophantine方程(2)在形如式(4)的分解下无整数解。

由引理4,Diophantine方程(2)另可分解形式为

k=±1,±2,…

当k=1时,即可化简为

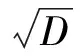
故有

因为24≡24(mod25),而

5αa4b+10Dαa2b3+D2αb5+βa5+

10Dβa3b2+5D2βa2b4≡0(mod25)

矛盾,所有该种情形下方程(2)也不存在整数解,证毕。

[1] 呼家源,李小雪.Diophantine方程x2+2m=yn的全部解[J].数学的实践与认识,2015,45(24):291-296.

[2] 袁平之,张中峰.丢番图方程X2-(a2+4p2n)Y4=-4p2n[J].数学学报(中文版),2014,57(2):219-222.

[3] 张中峰,罗家贵.丢番图方程x2-By2p=z3[J].数学学报(中文版),2014,57(1):195-198.

[4] 邬毅,龙兰.Euclid域中Diophantus方程的整数解[J].数学杂志,2015,35(4):1012-1016.

[5] 王振,李小燕.关于不定方程x2+11=4y3[J].重庆工商大学学报(自然科学版),2009,26(6):551-552.

[6] 曹珍富.丢番图方程引论[M].哈尔滨:哈尔滨工业大学出版社,2012.

[7] 邬毅,张正萍,龙兰.Euclid域中丟番图方程整数解的进一步讨论[J].重庆理工大学学报(自然科学),2016,30(5):132-134.

[9] 许宏鑫,赵西卿.关于两个Diophantine方程的求解[J].甘肃科学学报,2016,28(4):9-12.

[10]潘承洞,潘承彪.代数数论[M].3版.济南:山东大学出版社,2001.

[11]邬毅,杨懿,龙兰,等.关于二次域理论求解一类Diophantus方程的整数解[J].数学杂志,2015,35(5):1197-1200.

[12]许宏鑫,赵西卿.实二次Euclid域中不定方程的整数解[J].重庆理工大学学报(自然科学),2016,30(9):151-155.

(责任编辑 何杰玲)

Solving the Integer Solutions of a Class of Diophantine Equations on Real Quadratic Euclid Fields

ZHAO Xi-qing, DONG Xiao-ming, ZHANG Xin, YANG Zhi, HONG Xia, WANG Wei-wei

(School of Mathematics and Computer Science, Yan’an University, Yan’an 716000, China.)

We studied the integer solutions of class typical Diophantine equations on real quadratic Euclid fields. By using some theories on quadratic fields and fundamental theorem of arithmetic on the ring of quadratic algebraic integer, we proved that the equations didn’t have integer solution.

Diophantine equation; real quadratic euclid fields; integer solution

2017-01-05

陕西省教育厅科研计划资助项目(2013JK0557);2015年陕西省大学生创新训练计划项目(1445)

赵西卿(1965—),男,河南偃师人,硕士,副教授,主要从事解析数论研究，E-mail: yazhaoxiqing@126.com。

赵西卿,董晓明,张昕,等.[J].重庆理工大学学报(自然科学)，2017(6):188-190.

format：ZHAO Xi-qing, DONG Xiao-ming, ZHANG Xin, et al.Solving the Integer Solutions of a Class of Diophantine Equations on Real Quadratic Euclid Fields[J].Journal of Chongqing University of Technology(Natural Science)，2017(6):188-190.

10.3969/j.issn.1674-8425(z).2017.06.029

O156.4

A

1674-8425(2017)06-0188-03