十字形柱的力学性能分析

滕振超，赵添佳

(东北石油大学 土木建筑工程学院， 黑龙江 大庆 163318)



十字形柱的力学性能分析

滕振超，赵添佳

(东北石油大学 土木建筑工程学院， 黑龙江 大庆 163318)

通过ABAQUS软件建立了钢筋混凝土十字形柱的有限元模型，并根据2根试件对模型的正确性加以验证，同时对9根十字形轴压柱进行数值分析，主要研究混凝土强度以及配筋率对十字形柱的力学性能影响。结果表明：对于混凝土强度相同的十字形柱，配筋率的增大对其延性有明显的改善，并且承载能力也有所提高；而随着混凝土强度的提高，配筋率对十字形柱的极限承载力影响会有一定减弱。

ABAQUS；十字形柱；混凝土强度；配筋率

随着我国生活质量的不断提高，人们对于建筑物的品质需求不断提高。在传统的建筑物结构中，结构柱限制了建筑物内部的设计以及家具的布置，降低了室内面积的有效利用率[1-6]。结构设计人员在保证结构安全可靠的前提下不断创新，丰富了建筑形式和建筑风格，使建筑物更加美观，同时使用功能更具灵活性和方便性，因此异形柱便应运而生。异形柱是目前新兴的一种柱体形式，较为广泛地应用于新型建筑物中[7-8]。异形柱是指其截面形式是L形、T形以及十字形等的柱体。该种柱体的优点是有效避免了室内出现明显结构柱，使整个建筑格局更加美观，有效地增大了建筑物的使用面积。其中，十字形柱在实际应用中最为广泛。但目前我国对于十字形柱理论上的学术成果还很十分匮乏，故对其力学性能研究显得尤为必要[9-11]。

对钢筋混凝土十字形轴压柱的研究采用试验和数值仿真的方式，在试验的基础上对十字形柱建立基于ABAQUS有限元软件的数值模型，得出混凝土强度以及配筋率对十字形柱力学性能的影响规律。

1 试验

1.1 试件设计

本文研究的十字形柱肢厚200 mm,肢长150 mm，柱体高度为1 200 mm，共12根纵筋，用箍筋构造配筋，由于该种柱体试件制作复杂，因此仅对2根柱体进行试验研究。本文试验试件具体参数如表1所示，十字形柱体截面形式如图1(a)所示。

表1 试件参数

1.2 测点布置

两个量程为50 mm的百分表分别布置在加载试验机下承压板上，并且采用对称布置方式，同时加载试验机的数据采集系统对构件的轴向位移数据进行提取。对以上所有轴向位移数据进行筛选并加权平均后得到试件的轴向位移。位移计具体布置情况如图1(b)所示。

图1 十字形柱体截面图及位移计布置

1.3 加载方案

本次试验加载设备为500 t级的YAW-5000微机控制电液伺服压力试验机。试验采用单调加载方式，荷载由试验机传感器采集，轴向位移由试验机传感器以及位移计同时采集。

加载前调整试件，保证其轴心受压。首先预估试件的极限荷载，且先预加载10%，目的是使试件能够与上下承压板接触良好，同时也能使试件几何中心与加载板对齐，直至调整试件、仪表完成，开始正式加载。起初以预估荷载的10%进行分级加载，每级加载待各个仪表示数稳定后，记录位移值，直至加载到预估极限荷载的70%后，以极限荷载的5%分级加载[12]，直至十字形柱的柱肢混凝土被压碎，试验停止。

2 试验荷载位移曲线分析

图2 试件荷载位移关系曲线

3 有限元模型建立

3.1 试件设计

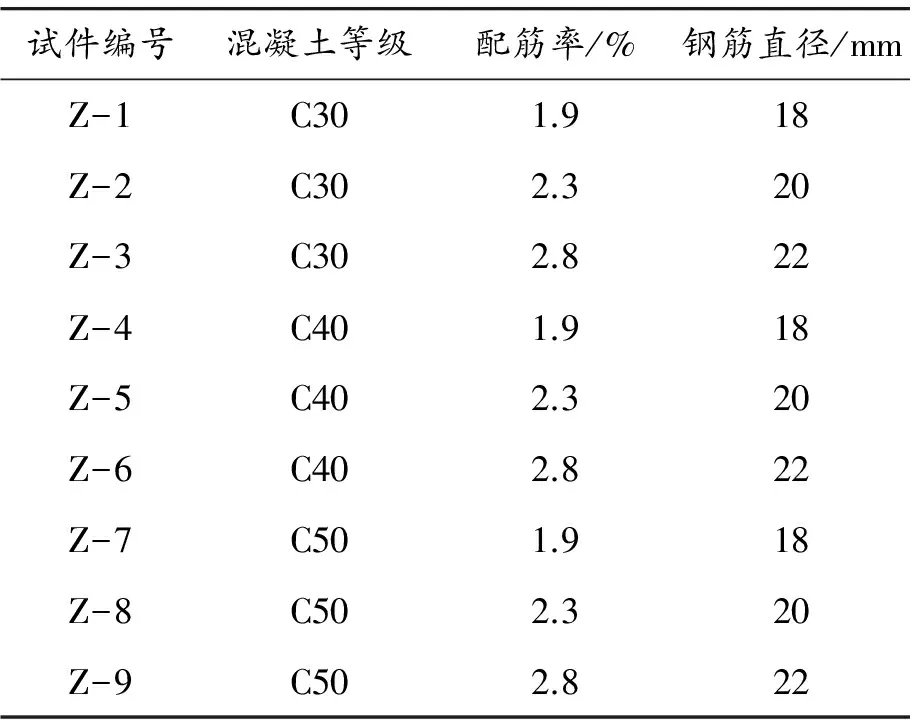
表2 模拟试件参数

3.2 建模过程

在建立有限元模型过程中混凝土采用损伤塑性模型，钢筋本构关系采用经典的双线性随动强化材料模型。钢筋通过合并形成钢筋笼，内置到整个柱体区域中。试件材料以及边界条件根据试验的实际情况进行设定和简化，使模拟结果更接近于试验值[13]。具体的建模过程如图3所示。

图3 建模过程示意图

3.3 材料参数

在定义材料属性时，材料的弹性模量、泊松比以及密度等方面的相关参数如表3所示。

表3 材料参数

4 模型验证

由图4可知：试验曲线与有限元模拟曲线变化趋势一致，极限荷载相差较小，拟合效果良好，说明有限元模型具有一定的可信度和精确度。由于本文所建立的有限元十字形柱体模型未考虑纵向受力钢筋与混凝土之间所存在的相对滑移，而是假定在整个受力过程中二者咬合良好，所以模拟值与文献中的试验值存在一定的偏差，但是模型基本能够真实反映试件的实际受力情况。

图4 荷载位移曲线对比

5 有限元分析

5.1 应力云图分析

根据有限元计算模型，可以分别提取9组十字形柱的应力变形图，由于其应力图较为相近，在此以Z-1为例(如图5所示)进行分析。

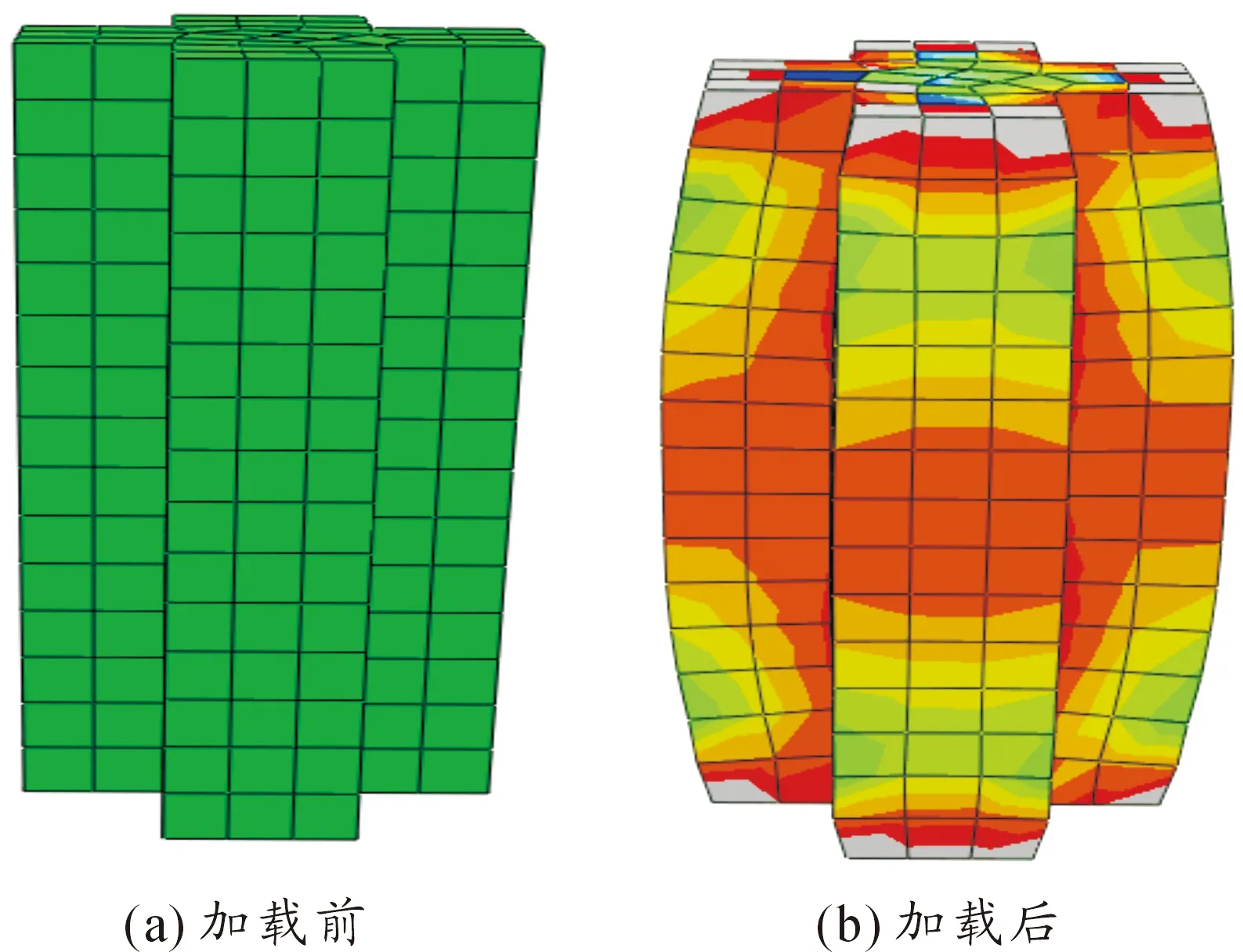
图5 加载前后应力及变形

由如图5可知：十字形混凝土柱在轴向荷载作用下，从几何变形角度看，柱体中部向外侧发生鼓曲，横向变形明显，混凝土柱体呈现灯笼状破坏；从应力分布角度看，等效应力最大位置处于十字形柱体中间部位，且由柱体核心混凝土区域向柱肢扩展，十字形柱体端部应力较小。其主要原因为：十字形柱对轴向荷载有很好的传递作用，使荷载主要集中在试件的中部，并且由于柱肢的影响，应力分布沿着柱高方向非环向分布而呈拱形分布。

图6 荷载轴向位移曲线

5.3 承载力分析

分别提取十字形柱有限元模型中，各个试件的极限承载力的具体数值如表4所示。

表4 十字形柱极限承载力

从表3可以得出：在混凝土强度相同情况下，C30组试件中相比Z-1，试件Z-2、Z-3极限承载力分别提高14%和22%,C40、C50组情况相同。由此可以得出：配筋率的提高对承载力有明显的提升作用，但混凝土等级提高后，配筋率对承载力影响明显减小。将C40、C50组试件与C30组相同配筋率的试件相比较可发现：提高相同混凝土等级，承载力提高幅度近似相同。其主要原因是：由于混凝土强度提高，十字形柱体的整体刚度变大，纵筋与箍筋所形成的钢筋笼对柱体核心混凝土的约束作用效果不再明显，因此较高混凝土等级试件的配筋率对承载力影响会明显削弱。

6 十字形轴压柱承载力计算

根据规范规定，混凝土柱体承载力N= 0.9φ(fcA+fy′As′)，其中：0.9为可靠度调整系数；短柱的稳定系数φ取值为1；fcA为混凝土承担的承载力；fy′As′为钢筋承担的承载力。根据公式可得各十字形柱极限承载力，如表5所示。

表5 十字形柱极限模拟与计算承载力对比

由表5可以看出：各组试件的模拟值与理论计算值的误差百分比均小于10%，理论计算结果与模拟结果相当接近，因此上述的有限元模型研究成果具有一定的可信度。

7 结论

本文通过试验验证了有限元模型的正确性，并且分别对轴向荷载作用下9根钢筋混凝土十字形截面柱进行数值仿真分析，主要结论如下：

1) 十字形柱在轴向荷载作用下，其破坏形式是柱体中部核心混凝土向外部鼓曲，横向变形明显呈现灯笼状。

2) 对于混凝土强度相同的十字形柱，配筋率的增大对其延性有明显的改善，并且承载能力也有所提高；而在混凝土强度提高的情况下，配筋率对试件的力学性能影响会有一定减弱。

3) 根据《混凝土结构设计规范》的计算公式、试验结果以及有限元模拟结果三者相互佐证，验证了公式在十字形柱中的适用性，同时也证明了有限元模型以及分析结果的正确性。

[1] CHEN Z Y,SHEN Z Y.Behavior of L-shaped concrete-filled steel stub columns under axial loading:Experiment[J].Advanced Steel Construction,2010,6(2):688-697.

[2] 李凯文，刘国华，万鑫,等.型钢高性能混凝土十字形异形柱抗震性能试验研究[J].工程抗震与加固改造，2015,37(6):8-14.

[3] 杜宏彪，管民生.钢筋混凝土异形柱框架结构Pushover分析研究[J].工程抗震与加固改造,2009,31(4):13-18.

[4] 屈立军，刘宝利.钢筋混凝土十字形轴压柱耐火性能的数值模拟研究[J].西安建筑科技大学学报,2000,32(4):393-396.

[5] 宋健，徐亚丰.反复荷载下十字形钢管混凝土芯柱抗震性能有限元分析[C]//第十一届全国现代结构工程学术研讨会.北京：[S.l],2011:1058-1059.

[6] 刁晓征，徐亚丰.十字形钢骨混凝土异形柱偏心受压试验研究[J].钢结构进展,2011,13(2):44-50.

[7] 苏益声，胡飞鹏，杨德磊.钢骨混凝上异形柱正截面承载力影响因素探讨[J].广西大学学报(自然科学版),2005,30(4):272-274.

[8] 邵永健，陈宗平，薛建阳,等.型钢混凝上异形柱轴压力系数限值的试验与理论分析[J].建筑结构学报,2007,28(6):153-159.

[9] 陈宗平，张喜德，苏益声,等.型钢混凝土异形柱正截面承载力的理论研究[J].2005,37(3):346-355.

[10]许成祥,刘晓强,杜国锋,等.十字截面钢管混凝土柱框架中柱节点抗震性能对比研究[J].武汉理工大学学报,2012,34(8):118-122.

[11]曲福来，黄承逵，赵欣.钢筋混凝土异形柱非线性分析[J].大连理工大学学报,2009,49(2):234-238.

[12]于洋，邬亚滨，张云峰,等.混凝土强度对GFRP管-混凝土-钢管组合柱性能的影响[J].郑州大学学报(理学版),2016,48(3):118-123.

[13]石亦平，周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社，2012.

(责任编辑 陈 艳)

Analysis of Mechanical Properties of Cross-Shaped Section Columns

TENG Zhen-chao, ZHAO Tian-jia

(College of Civil Engineering and Architecture，Northeast Petroleum University， Daqing 163318， China)

The finite element model of reinforced concrete cross-shaped section columns is established by ABAQUS software, and it verified the correctness of the model according to 2 test specimens, at the same time, numerical analysis is carried out on the 9 cross-shaped section columns, and the influence of concrete strength and reinforcement ratio on the mechanical properties of cross-shaped section columns is mainly researched. The results show that the cross-shaped section columns in the same concrete strength, with the increase of reinforcement ratio, the ductility is improved significantly and the bearing capacity is also to ameliorate; and the increase of concrete strength, the effect of reinforcement ratio on ultimate bearing capacity of cross-shaped section columns will be weakened.

ABAQUS; cross-shaped section column; concrete strength; reinforcement ratio

2016-12-18

国家自然科学基金资助项目(51308028)

滕振超(1976—)，男，河北故城人，硕士，副教授，主要从事土木工程结构抗震研究，E-mail: 1220508676@qq.com。

滕振超，赵添佳.十字形柱的力学性能分析[J].重庆理工大学学报(自然科学)，2017(6):78-83.

format：TENG Zhen-chao, ZHAO Tian-jia.Analysis of Mechanical Properties of Cross-Shaped Section Columns[J].Journal of Chongqing University of Technology(Natural Science)，2017(6):78-83.

10.3969/j.issn.1674-8425(z).2017.06.011

TU375.3

A

1674-8425(2017)06-0078-06