一种带搜索因子的全局最优人工蜂群算法

常扣扣,火久元,梅 凯

(兰州交通大学 电子与信息工程学院， 兰州 730070)



一种带搜索因子的全局最优人工蜂群算法

常扣扣,火久元,梅 凯

(兰州交通大学 电子与信息工程学院， 兰州 730070)

针对全局最优人工蜂群算法(GABC)搜索迭代过程中未充分考虑到全局优化和局部优化在优化过程中的作用，在一定程度上降低了算法的全局搜索能力，容易陷入局部最优解的问题，提出了一种带搜索因子的全局最优人工蜂群算法(HF-GABC)。在最优人工蜂群(GABC)算法中引入了可以随着优化过程动态搜索的因子，在算法的全局搜索过程和局部搜索过程中进行动态搜索。应用改进的算法对4个标准测试集函数进行仿真试验，并与ABC算法、GABC算法的结果进行比较。实验结果表明：带搜索因子的人工蜂群算法收敛性能优于ABC和GABC算法，有效降低了局部收敛的可能性，并且提高了搜索精度。

全局最优人工蜂群算法；全局优化；局部优化；动态调节；搜索因子

随着科技的进步，人们在工程领域所遇到的问题越来越复杂。研究人员根据生物群体所表现的行为，对其群体活动比如寻找食物的过程进行模拟，建立了一系列的数学模型，用于解决工程实践过程中的函数优化问题，即群体智能优化。群体智能是指复杂行为的特性由许多简单的个体通过相互交互表现出来的智能[1]。比较常见的群体智能仿生算法有人工蜂群算法(ABC)[2]、人工鱼群算法(AFSA)[3]、遗传算法(GA)[4]、粒子群优化算法(PSO)[5]等。

人工蜂群算法(artificial bee colony algorithm,ABC算法)是一种模拟蜜蜂群体合作觅食行为的群体智能优化算法，由土耳其学者Karaboga于2005年首次系统地提出[2]。由于该算法具有操作简单、控制参数较少、收敛速度较快、易于实现等特点，吸引了越来越多的学者研究，并广泛应用于实际的优化问题中。文献[6]针对K-means聚类算法中对初始聚类中心敏感、易陷入局部最优等缺点，提出一种基于K-means的人工蜂群聚类算法，提高了聚类算法的聚类效果，改善了K-means的稳定性。文献[7]利用人工蜂群算法解决了图形染色问题。

基本人工蜂群算法的函数优化过程中依靠贪婪性方法选择最优解，广度与深度搜索不够充分，搜索精度不高，容易陷入局部最优解，影响算法的性能。因此，许多学者进行了对基本ABC算法的改进研究。文献[8]引入混沌思想，降低了ABC算法陷入局部最优解的可能性，提高了搜索速度和精度。文献[9]提出一种基于细菌趋药性和当前最优解策略的人工蜂群算法，提高算法寻优性能。文献[10]提出了全局最优人工蜂群算法(gbest-guided artificial bee colony algorithm,GABC算法)。GABC算法提高了深度搜索能力，收敛速度也有了较大提升。但GABC算法未充分考虑到全局优化和局部最优在优化过程中的作用，导致算法的优化精度和优化效率提升不够。因此，本文提出了一种带搜索因子的GABC算法(HF-GABC)，通过增加可以根据进化过程动态变化的搜索因子来平衡人工蜂群算法的局部搜索和全局搜索能力，从而提升算法效率和提高算法精度。

1 基本人工蜂群算法(ABC算法)

人工蜂群算法模拟蜜蜂觅食机制进行函数优化问题的处理，基本人工蜂群算法模拟蜜蜂采蜜的过程，分为初始化阶段、雇佣蜂阶段、观察蜂阶段和侦查蜂阶段4部分[2]：① 初始化阶段：参数初始化，包括蜂群总数、最大迭代次数和最大停止次数。② 雇佣蜂阶段：根据其记忆在蜜源附近进行随机邻域搜索，并将蜜源信息传递给观察蜂。当蜜源开采完之后，雇佣蜂的角色变成侦查蜂。③ 观察蜂阶段：根据雇佣蜂传递的蜜源适应度信息进行优秀蜜源的选择，然后在其附近进一步搜索优秀蜜源。④ 侦查蜂阶段：放弃适应度差的蜜源并寻找新的蜜源。3种蜜蜂相互合作，最终达到函数优化的目的。算法流程如图1所示。

基本人工蜂群算法详细描述：

步骤1 初始化。算法随机生成SN个蜜源，蜂群数目为NP,最大迭代次数为maxcycle，最大停滞次数为limit，在给定的取值范围内按照式(1)随机产生SN个花蜜源信息：X={Xij|i=1,2,3,…,SN;j=1,2,3,…,D}，并根据式(2)计算该蜜源的适应度值fitness。

Xij=bj+rand(0,1)(aj-bj)

(1)

(2)

式(1)中rand(0,1)表示(0,1)之间的分布均匀的随机数，控制邻域搜索范围。D为优化空间的维数，aj和bj分别表示第j维数据的上限和下限。确定算法的结束条件和花蜜源停滞最大次数limit。

图1 ABC算法流程

步骤2 雇佣蜂阶段。雇佣蜂根据式(3)在其当前位置附近进行邻域搜索，产生1个新的候选蜜源并计算其适应度值fitness。

Vij=Xij+φij(Xij-Xkj)

(3)

式(3)中φij为[-1，1]之间的随机数，k不等于j。如果新的蜜源Vij的适应度好于Xij，则用新花蜜源Vij的位置代替旧花蜜源Xij的位置；否则，仍然维持旧花蜜源位置不变，同时将花蜜源的停滞次数加1。

步骤3 观察蜂阶段。在此过程中，观察蜂按照轮盘赌选择雇佣蜂搜索到的花蜜源，根据雇佣蜂更新花蜜源位置的方法对当前花蜜源进行位置更新，其中较优花蜜源有可能被多次更新，选择概率为

(4)

步骤4 侦察蜂阶段。统计每个花蜜源的停滞次数，当停滞次数达到limit仍没有找到适应度值更高的花蜜源时，则需要放弃当前的花蜜源，并根据给定的取值范围内随机产生一个新的花蜜源位置。

步骤5 判断解是否满足要求。记录当前的最优蜜源是否为全局最优位置，是则输出全局最优解，否则转步骤2进行下一次迭代。

2 全局最优人工蜂群算法(GABC算法)

在搜索过程中ABC算法的收敛性能受到蜜蜂深度搜索不够充分、优秀个体不能充分进化的影响。另外，人工蜂群算法缺乏对花蜜源最优解的保护，可能会导致最优花蜜源被抛弃，算法难以收敛于全局最优解。朱国普等[10]提出一种名为gbest-guided ABC algorithm(GABC) 的算法。该算法用式(5)取代原始ABC算法中的式(2)。

Vij=Xij+φij(Xij-Xkj)+φij(Yj-Xij)

(5)

式中：φij是[-1,1]中的一个随机数，是[0,C](C是一个正数)中的一个随机数；Yj是第j维空间的最优解。如果新的蜜源Vij的适应度好于Xij，则用新花蜜源Vij的位置代替旧花蜜源Xij的位置，否则，仍然维持旧花蜜源位置不变，同时将花蜜源的停滞次数加1并判断花蜜源的停滞次数是否达到limit。如果新的蜜源Vij的适应度好于Xij,则用新的花蜜源Vij代替旧的花蜜源Xij;否则仍然维持旧的花蜜源，并判断花蜜源的停滞次数是否达到limit。依此规律，将所有的雇佣蜂所携带的花蜜源信息更新完毕。

3 GABC算法的改进及实验

在GABC算法中，仍然保留着ABC算法的主要特性。GABC算法通过蜜蜂个体进行搜索并根据个体与邻域之间的共享信息探索较高质量的花蜜源。在寻优过程中，随着搜索的进行，邻域个体之间的共享信息会减少。由于蜜蜂的寻优过程并没有和邻域个体位置之间的扰动系数φij相结合，因此GABC算法未充分考虑到全局优化和局部最优在优化过程中的作用，通过φij(Yj-Xij)项来平衡算法的探索和开发能力在一定程度上降低了算法的全局寻优能力，没有更好地体现出对蜂群寻优进程的控制，导致算法的优化精度和优化效率提升仍然不够。因此，本文针对GABC算法中存在的缺陷，提出一种改进GABC算法，即带搜索因子的GABC算法。

3.1 带搜索因子的GABC算法

为了提高GABC算法的广度搜索和深度搜索能力，本文结合文献[11]和[12]引入了搜索因子，通过调整搜索因子，动态地控制算法的搜索能力，提出了一种带搜索因子的GABC算法(HF-GABC)。在搜索过程中，为了进一步控制蜜蜂个体间的信息共享程度和算法的全局搜索精度，本文引入了2个搜索因子：局部搜索因子和全局搜索因子。基于搜索因子的GABC算法用式(6)代替式(5)进行搜索：

Vij=Xij+δφij(Xij-Xkj)+λφij(Yj-Xij)

(6)

图2 全局搜索因子和局部搜索因子随迭代次数的变化取值

3.2 HF-GABC算法的性能测试

为了验证改进后算法HF-GABC的优化性能，与ABC、GABC进行对比实验。参数设置：最大迭代次数maxcycle=5 000,种群个数NP=20,蜜源个数SN=10，最大停滞次数limit=100。选取4个标准测试集函数进行性能测试，每个测试函数独立运行30次，取平均值。测试集函数属性如下所示：

Griewank函数：

[-600,600]D

Rastrigin函数：

[-5.12,5.12]D

Sphere函数：

Rosenbrock函数：

[-50,50]D

f1和f2函数为多峰值函数，理论最优值为0；f3和f4函数为单峰值函数，理论最优值也为0。

实验在系统为32位win7系统、处理器为Intel(R) Core(TM)i3、内存为4G的计算机上实现。程序采用java语言实现。表1是ABC、GABC、HF-GABC三种算法对上述4种函数进行优化的实验结果比较。

由表1可见：对于多峰值函数Griewank(当D=30和D=60)和Rastrigin(当D=30和D=60)，HF-GABC的优化效果更好，尤其是对Rastrigin，能达到理论上的最优值；对于难以优化的单峰值函数Sphere(当D=30和D=60)和Rosenbrock(当D=2和D=3)，HF-GABC的优化效果比ABC和GABC更优。改进之后的HF-GABC的均值与方差均优于ABC算法和GABC算法，在收敛精度和算法稳定性上更优。

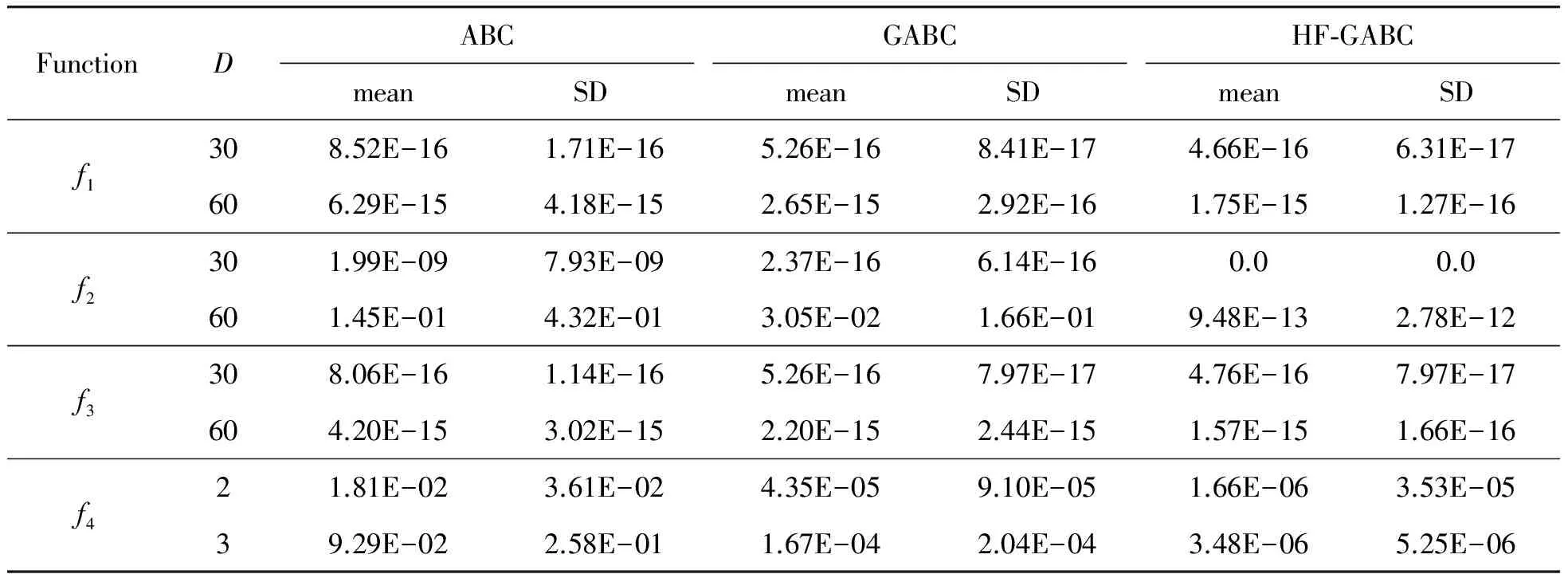
表1 3种算法对标准函数优化结果比较

由图3～10可知：由于在算法初始化时采用的随机策略，故3种算法的初始最优值并无明显差别。随着算法的不断迭代，3种算法不断改善当前最优值。ABC算法出现了最优解的丢失现象，由于对最优解保护的缺乏，所以收敛精度也相对较差。GABC算法虽能在较少的迭代次数内找到较优的解，但全局寻优结果仍不理想。HF-GABC算法获得了最优的结果，且算法向好的方向收敛的性能可得到保证。

图3 Griewank函数为30维时的优化过程

图4 Griewank函数为60维时的优化过程

图5 Rastrigin函数为30维时的优化过程

图6 Rastrigin函数为60维时的优化过程

图7 Sphere函数为30维时的优化过程

图8 Sphere函数为60维时的优化过程

图9 Rosenbrock函数为2维时的优化过程

图10 Rosenbrock函数为3维时的优化过程

4 结束语

HF-GABC算法是在GABC算法基础上，充分考虑到全局优化和局部最优在优化过程中的作用，加入了搜索因子，可以更好地控制GABC算法的优化过程，在保证算法开发能力的同时整体提高了算法的全局寻优能力，降低了陷入局部最优的可能性，使算法能在较短的时间内获得收敛。与ABC、GABC算法的对比实验结果表明： HF-GABC算法无论是在搜索精度还是算法稳定性方面均具有更好的性能优势。

[1] BONABEAU E,DORIGO M,THERAULAZ G.Swarm Intelligence:From Natural to Artificial Systems[M].New York:Oxford University Press,1999.

[2] KARABOGA D,AKAY B.A Comparative Study of Artificial Bee Colony Algorithm[J].Applied Mathematics and Computation.2009,214(1):108-132.

[3] 李晓磊.一种新型的智能优化方法-人工鱼群算法[D].杭州：浙江大学,2003.

[4] HOLLAND J H.Adaptation in natural and artificial system:an introductory analysis with applications to biology,control,and artificial intelligence[M].2nd ed.Cambridge:MIT Press,1992.

[5] KENNEDY J,EBERHART R C.Partucle Swarm Optimization[C]//Proc.of IEEE International Conference on Neural Networks,IV.Piscataway,NJ,USA:IEEE Service Center,1995:1942-1948.

[6] KARABOGA D,AKAY B.A Comparative Study of Artificial Bee Colony Algorithm[J].Applied Mathematics and Computation.2009,214(1):108-132.

[7] 曹永春，蔡正琦，邵亚斌.基于K-means的改进人工蜂群聚类算法[J].计算机应用，2014，34(1)：204-207.

[8] MOHAMADI S A,DERAKHSHI M R F,AKBARI R.ANAdaptive Multi-Objective Artificial Bee Colony with Crowding Distance Mechanism[C]//Proceedings of 16thCSI International Symposium on Artificial Intelligence and Signal Processing.Shiraz:[s.n.],2012:68-73.

[9] 周长喜，毛利，吴滨，等.基于细菌趋药性和当前最优解策略的人工蜂群算法[J].计算机应用与软件，2016，33(1)：268-272.

[10]王冰.基于局部最优解的改进人工蜂群算法[J].计算机应用研究，2014，31(4)：1023-1026.

[11]ZHU Guopu.Sam Kwong Gbest-guided artificial bee colony algorithm for numerical function optimization[J].Applied Mathematics and Computation,2010,217(7):3166-3173.

[12]王辉.一种带共享因子的人工蜂群算法[J].计算机工程，2011,37(22)：140.

[13]刘立群.基于全局共享因子的混合蛙跳算法[J].计算机工程，2013,39(10)：163.

(责任编辑 杨黎丽)

A Gbest-Guided Aritificial Bee Colony Algorithm with Hunting Factor

CHANG Kou-kou, HUO Jiu-yuan, MEI Kai

(School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Aiming at the problem that the Gbest-guided artificial bee colony (GABC) algorithm is not considered the role of global optimization and local optimization in the optimization process in the iterative process, and is easily to fall into the local optimal solution, a Gbest-guided ABC algorithm based on hunting factor (HF-GABC) is proposed in this paper. In the Gbest-guided artificial bee colony algorithm for numerical function optimization (GABC), the factors that can be dynamically hunted with the optimization process are introduced in the process of global optimization and local search. The simulation experiments were taken on four standard test functions and the improved algorithm were compared with the ABC algorithm and the GABC algorithm. The experimental results show that the convergence rate of HF-ABC algorithm performs better than the ABC and GABC algorithm, which effectively reduces the possibility of local convergence and improves the search precision.

Gbest-guided artificial bee colony algorithm; global optimization; local optimization; dynamic regulatory; hunting factor

2017-03-05

国家自然科学基金资助项目(61462058)；兰州市科技计划资助项目(2014-1-127)；兰州市人才创新创业科技计划资助项目(2014-RC-4)

常扣扣(1991—),男,安徽宿州人,硕士研究生,主要从事智能计算、数据挖掘等研究，E-mail:929775937@qq.com； 火久元(1978—),男,甘肃兰州人,博士研究生,副教授,主要从事智能计算、数据挖掘等研究，E-mail:huojy@lzb.ac.cn。

常扣扣,火久元,梅凯.一种带搜索因子的全局最优人工蜂群算法[J].重庆理工大学学报(自然科学)，2017(6):160-165.

format：CHANG Kou-kou, HUO Jiu-yuan, MEI Kai.A Gbest-Guided Aritificial Bee Colony Algorithm with Hunting Factor[J].Journal of Chongqing University of Technology(Natural Science)，2017(6):160-165.

10.3969/j.issn.1674-8425(z).2017.06.024

TP301.6

A

1674-8425(2017)06-0160-06