无线传感器网络中基于采样的时空数据恢复

陈业斌， 王仁伟，李 颖

(1.安徽工业大学 计算机科学与技术学院, 安徽 马鞍山 243032；2.马鞍山师范高等专科学校 教师教育系， 安徽 马鞍山 243041)



无线传感器网络中基于采样的时空数据恢复

陈业斌1， 王仁伟1，李 颖2

(1.安徽工业大学 计算机科学与技术学院, 安徽 马鞍山 243032；2.马鞍山师范高等专科学校 教师教育系， 安徽 马鞍山 243041)

随着智慧城市步伐的深入，对物理环境感知的要求越来越高；无线传感器网络被广泛部署到真实环境中去收集各种各样的环境数据，比如温度、湿度、光照度和二氧化碳的含量等。当无线传感器网络的规模很大时，巨大的数据传输量严重阻碍了无线传感器网络的长时间有效运行。矩阵填充作为一个新的稀疏表示技术，可以通过低秩矩阵中少量随机采样进行数据重构。由于传感数据的时空相关性，相邻传感器节点和时间节点的数据信息相对冗余，故采用分块采样的策略进行稀疏采样，在保证恢复精度的同时降低采样率，以达到降低数据传输代价的目的。

无线传感器网络；稀疏采样；矩阵填充；采样策略

随着信息技术的高速发展，无线传感器网络被广泛部署在网络空间中[1],用来收集各种各样的传感数据。ExScal[2]使用1 000个以上传感器节点进行网络入侵检测。CitySee系统[3]被用来连续收集环境数据，包括温度、湿度、光照度和二氧化碳的含量等。无线传感器网络通常希望能长时间收集环境传感数据。然而，传感器节点的物理限制和大量数据的传输阻碍了传感器网络的长时间有效运行。利用部署在真实环境中的传感数据的时空相关性和稀疏表示技术，通过收集小部分数据可以高精度恢复所有的监测数据。

近年来，很多稀疏表示方法[5-7]已经被用来降低无线传感器网络中的采样代价。目前存在的方法可以分为基于压缩感知的数据收集和基于低秩矩阵填充的数据重构2种。基于压缩感知的数据收集技术利用数据向量的组合来降低数据的传输量。C.Luo等[5]提出一个大规模压缩数据收集方案，可在每一条链路上降低传输代价和均衡能量代价。尽管基于压缩传感的数据收集技术能降低传输代价，但是它只能利用时间或者空间信息来降低采样数量。同时，链路错误会严重影响传感数据的恢复效果[9]。为了利用传感数据的时空相关性，J.Cheng等[7]提出一个基于低秩矩阵填充的时空压缩数据收集技术,相对于基于压缩传感的收集技术能进一步降低传输代价。在文献[10-11]中，当无线传感器网络中数据的丢失率变得很大时，低秩矩阵填充理论被提出来重构传感数据。众所周知，目前存在的基于矩阵填充的数据收集技术都是假设传感数据矩阵的秩是已知的，然而由于监测数据通常是未知的，故传感数据的秩很难计算。与此同时，真实的传感数据实验结果显示：传感数据矩阵的秩会随时间动态变化。

为解决监测数据矩阵秩的不确定导致采样数量不确定的问题，本研究采用了采样终止条件[8]。由于传感数据具有时空相关性，相邻传感器节点和时间节点的数据信息相对冗余，为降低采样率采用分块采样的策略，从而减少了数据的传输代价。

1 问题描述

1.1 低秩矩阵填充

矩阵填充是一个通过已知的部分矩阵元素来恢复整个低秩矩阵的新技术。假设存在矩阵M∈Rn1×n2,其中，M矩阵的(i,j)位置的元素用Mij来表示，则(i,j)的全集用Ω表示。故矩阵填充的问题就是用根据部分已知元素来恢复未知元素得到新的矩阵X，并且使得X的秩最小。矩阵填充问题的数学模型如下：

min rank(X)

s.t.PΩ(X)=PΩ(M)

(1)

采样操作PΩ：Rn1×n2→Rn1×n2的定义如下：

(2)

由于这是一个NP-hard问题，可以用以下凸优化模型来代替：

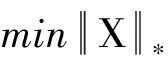
s.t.PΩ(X)=PΩ(M)

(3)

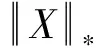
m≥C*n6/5*r*logn

(4)

其中n=max{n1,n2}。

1.2 问题介绍

近年来，随着社会经济生活的快速发展，环境保护问题越来越受到人们的关注。世界各国都在致力于控制和减少环境污染，研究环境可持续发展的绿色方案。我国也提出了低碳经济的战略目标，并对环境监控提出了更高的要求。

基于无线传感器网络的环境监测可将大量微型传感器节点随机部署到感兴趣的区域中，对特定区域的环境信息进行间断或者连续地采样，自动积累环境的长期监测数据。在对环境进行监控时，需要实时对无线传感器网络数据进行采样、传输、处理等流程。由于传感器网络中数据量庞大，遍历采样需要巨大的代价，故可以通过矩阵填充技术来减少采样数量以降低环境监控的成本。为了进一步降低采样数量，可以充分利用传感器网络历史数据进行矩阵恢复。

在一个传感器网络中，存在M个节点，每一个节点每隔一段时间会采集一次环境数据，则在N个时间段就生成数据矩阵XM×N，历史数据也存储在数据库中。故假设从历史数据中截取矩阵X1，在XM×N中稀疏采样，并根据X1得到XM×N的恢复矩阵。

1.3 问题建模

令XM×N为X2，则X=[X1;X2],其中X1的维度是M×N1，X2的维度是M×N2，并且X1已知，X2未知。本文使用二值采样矩阵D。已知或者已采样的元素为1，其余的为0，D的定义如下：

(5)

定义采样矩阵S来记录原始测量数据。矩阵S是一个不完整的监控数据矩阵，可以表示为

SM×(N1+N2)=X*D

(6)

其中*代表两个矩阵的点积，即Sij=Xij×Dij。根据前面介绍的矩阵填充技术，当采样数量足够时，X可以通过如下公式从S中恢复得到：

s.t.S=X*D

(7)

定义从式(7)中恢复得到矩阵为X～。

1.4 挑战

尽管前面介绍矩阵填充是从子数据集中高精度恢复数据，但是前提条件是需要知道数据矩阵的秩。然而，传感器网络中数据的秩未知，因此遇到的挑战如下：为降低采样代价，则冗余的采样数量则应该最小。然而，根据矩阵填充理论，由于不知道数据矩阵的秩，很难知道采样数量是否足以达到准确恢复的目的。

本文发现误差的奇异点都集中在某些区域，为提高恢复精度，需要设计一个更有效的采样策略来发现误差奇异值区域，而不是采用简单随机采样策略。然而，由于不知道数据矩阵结构，故设计采样策略是一个难点。

2 解决方案

2.1 采样策略

由于测量矩阵的秩未知，很难知道多少采样数量是足够的，故本文提出分块自适应连续采样策略。相对于后期的采样数量，本文在初始采样时设置一个较小的值，然后根据需要恢复的数据矩阵确定是否需要进行更多的样本采样。那么采样的终止条件是什么呢？

对于一个低秩矩阵X，给出t和t+1两个连续采样步骤，其中第t步采样m个样本，t+1额外采样C个样本。这两个采样步骤得到的恢复矩阵分别为X～(t)和X～(t+1)，如果X～(t)=X～(t+1)，则X～(t)精确等于矩阵X。

定义1 给出连个矩阵AN×N和BN×N，定义A≅B，只要满足如下条件：

≤ε

(8)

其中ε是一个非常小的常数。

定义2 采样终止条件

定义经过连续t和t+1两个采样步骤矩阵填充操作恢复出的数据分别为X～(t)和X～(t+1)。如果这两个数据矩阵满足X～(t)=X～(t+1)，那么认为传感器网络数据在第t步已经准确地恢复出来，在第t+1步终止采样操作。本文会给出理论证明。

在一个在线的监测系统中，很难知道相关矩阵的特征和秩。在简单的随机采样中，随着采样率地提高，恢复的精度和效果越来越高，最终达到一个稳定的状态。然而简单随机采样带有冗余采样。为在提高恢复准确率的同时降低整个采样数，需要进行智能化采样。考虑到t和t+1是两个连续采样步骤，令S(t)和S(t+1)分别代表这两步骤的采样矩阵，很明显S(t)∈S(t+1)，恢复出的数据分别为X～(t)和X～(t+1)。当采样率很低时，整个数据矩阵恢复不理想的数据都集中在某些区域中。针对这一问题，本文采用分块的思想，把整个数据均匀分割成若干小块。由于X=[X1;X2]，X1已知，对X进行分块，如图1所示。

图1 X的采样结构分布

(9)

计算第K个分块的每一个元素的INFO值，并统计均值EK和方差SK。评估第K个分块的恢复情况，用INFOK来表示：

INFOK=a*EK+b*SK

(10)

如果分块K的INFOK很大，这意味着这个分块的恢复效果不是很理想，需要在下一步增加采样量。因此，本文的采样策略就是在恢复不理想的分块中增加采样量，INFOK值越大，需要采样的数量就越多。

2.2 理论分析

本文定义LM是矩阵X精确恢复的最低采样阈值。由于X=[X1;X2]，则LM1是X1的最低采样阈值，LM2是X2的最低采样阈值，故有LM=LM1+LM2。m是第t步的采样数，m+C是第t+1步的采样数。要证明X～(t)=X～(t+1)成立的条件是m+C>m>LM。由于X=[X1;X2]，则有m=m1+m2，m1是在X1中的采样数，m2是在X2中的采样数。则有：

m1+m2+C>m1+m2>LM1+LM2

(11)

对不等式三边同时减去LM1得：

m1-LM1+m2+C>m1-LM1+m2>+LM2

(12)

令m1-LM1=δ>0，那么有

m2+C+δ>m2+δ>LM2

(13)

为证明X～(t)=X～(t+1)成立的条件是上面的表达式，本文的证明分为3个部分：

1) 当m2+C+δ>m2+δ>LM2时，很明显有X～(t)=X～(t+1)=X。 2) 当m2+C+δ>LM2>m2+δ时，X2～(t+1)=X2，X2～(t)≠X2，因此X～(t)≠X～(t+1)。

因此，综合上面3种情况，本文得出X～(t)=X～(t+1) 成立的条件是m+C>m>LM。

2.3 算法实现

算法实现流程见表1。

3 实验过程及结果

3.1 传感器网络数据

本研究的数据来源于无锡清华信息科学与技术国家实验室GreenOrbs(绿野千传)系统。关于GreenOrbs的详细信息请参考文献[14]。GreenOrbs系统[15]在森林部署330个传感节点，以监控森林的湿度、光照、二氧化碳等环境参数。实景分布图和网络拓扑图如图2所示。

表1 算法实现流程

图2 GreenOrbs的实景分布图的拓扑图

3.1.1 硬件

GreenOrbs的传感器节点是TelosB，其中该节点的处理器和收发器分别是MSP430和CC420，程序闪存为48 KB，测量串口闪存为1 024 KB，RAM是10 KB。

3.1.2 软件和协议

GreenOrbs传感器节点的操作系统是TinyOS2.1。主要的数据流是链路节点中多跳数据收集。同时，FTSP协议[16]的功能使得全网同步。

3.2 传感器网络数据预处理

本文的实验数据是一个真实的传感器网络数据，传感器网络有部分节点未采集到数据，故传感器网络历史数据存在部分零值的元素使得矩阵的秩很高，需要对历史数据进行预处理操作，本文使用奇异值收缩的方法进行预处理，具体操作如下：

对X∈Rn1×n2进行奇异值分解如下：

X=U×∑×V*, ∑=diag({σi})

对于每个τ≥0，有软阈值操作Dτ:

Dτ(X):=U×Dτ(∑)×V*

Dτ(∑)=diag({σi-τ}+)

其中τ+表示τ的非负部分，即τ+=max(0,τ)。这个软阈值操作仅仅应用在矩阵X1的奇异值上，使它们趋于0，这样可以降低X1的秩。

3.3X1对X2恢复的影响

在矩阵填充的理论中，随着采样率的提高恢复精度也会越来越高，然而在恢复效果很好时，相应的采样率又很大。为了在保证恢复精度的同时降低采样率，采样传感器网络历史数据X1来降低X2采样率。在X2相同采样率下，对比X1对X2的恢复影响，如图3所示。

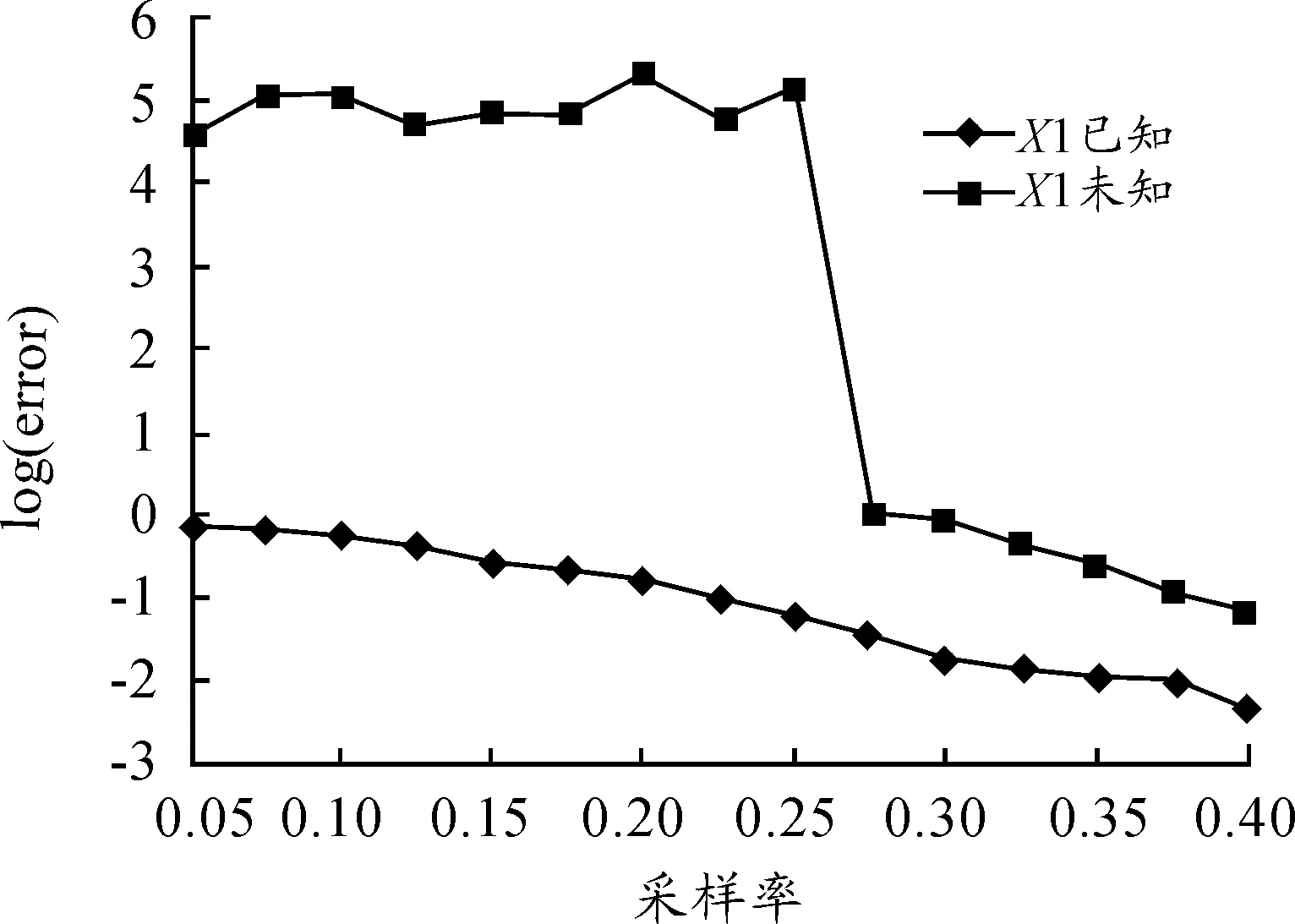
图3 X1对X2恢复的影响

3.4ε对X2恢复的影响

根据采样终止条件，当采样终止条件触发时，X～(t)和X～(t+1)之间的差距小于阈值ε。为了验证ε对X2恢复精度和采样率的影响，使用不同的ε运行本文的算法。实验结果如图4、5所示。

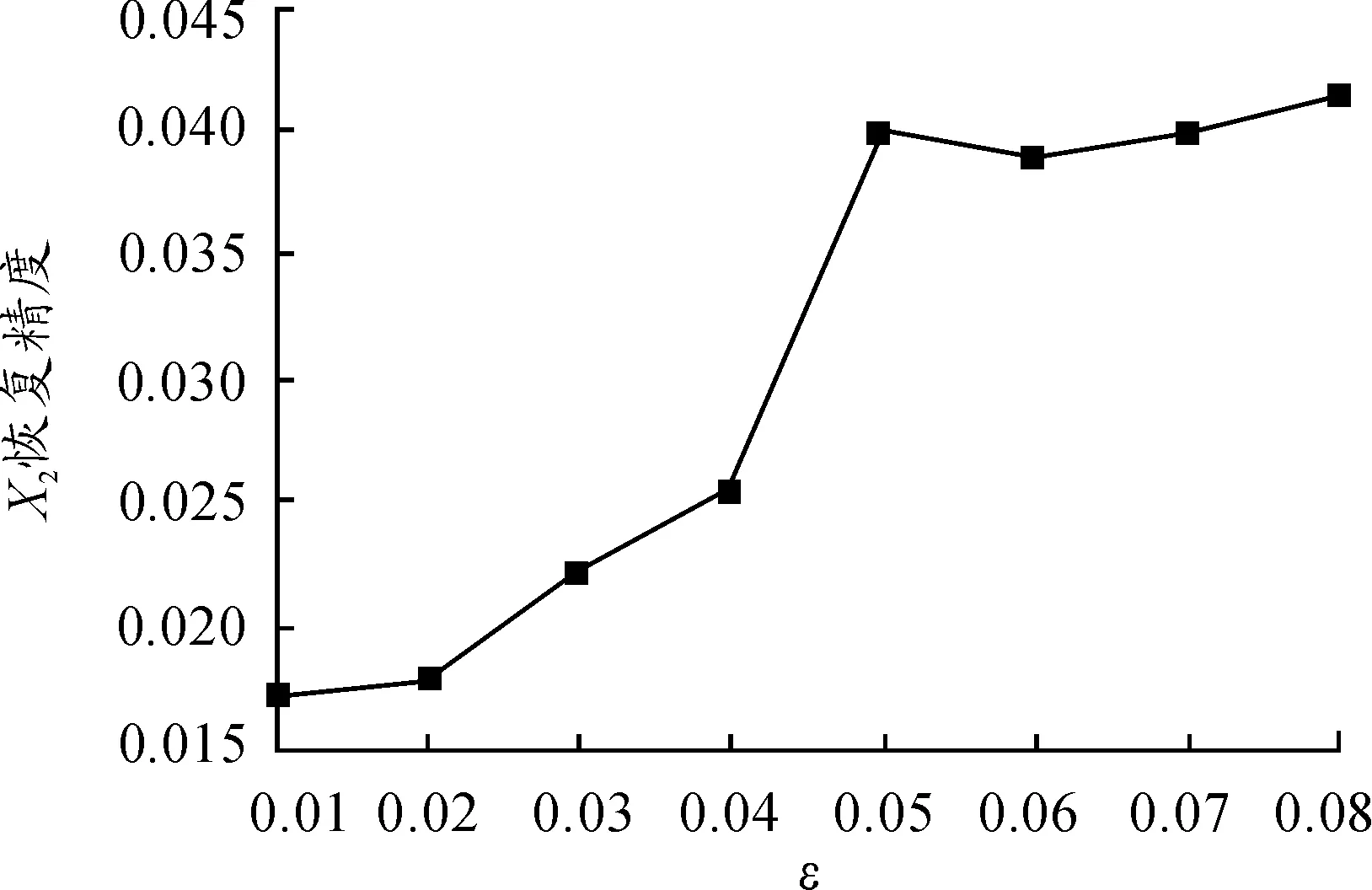
图4 对X2恢复精度的影响

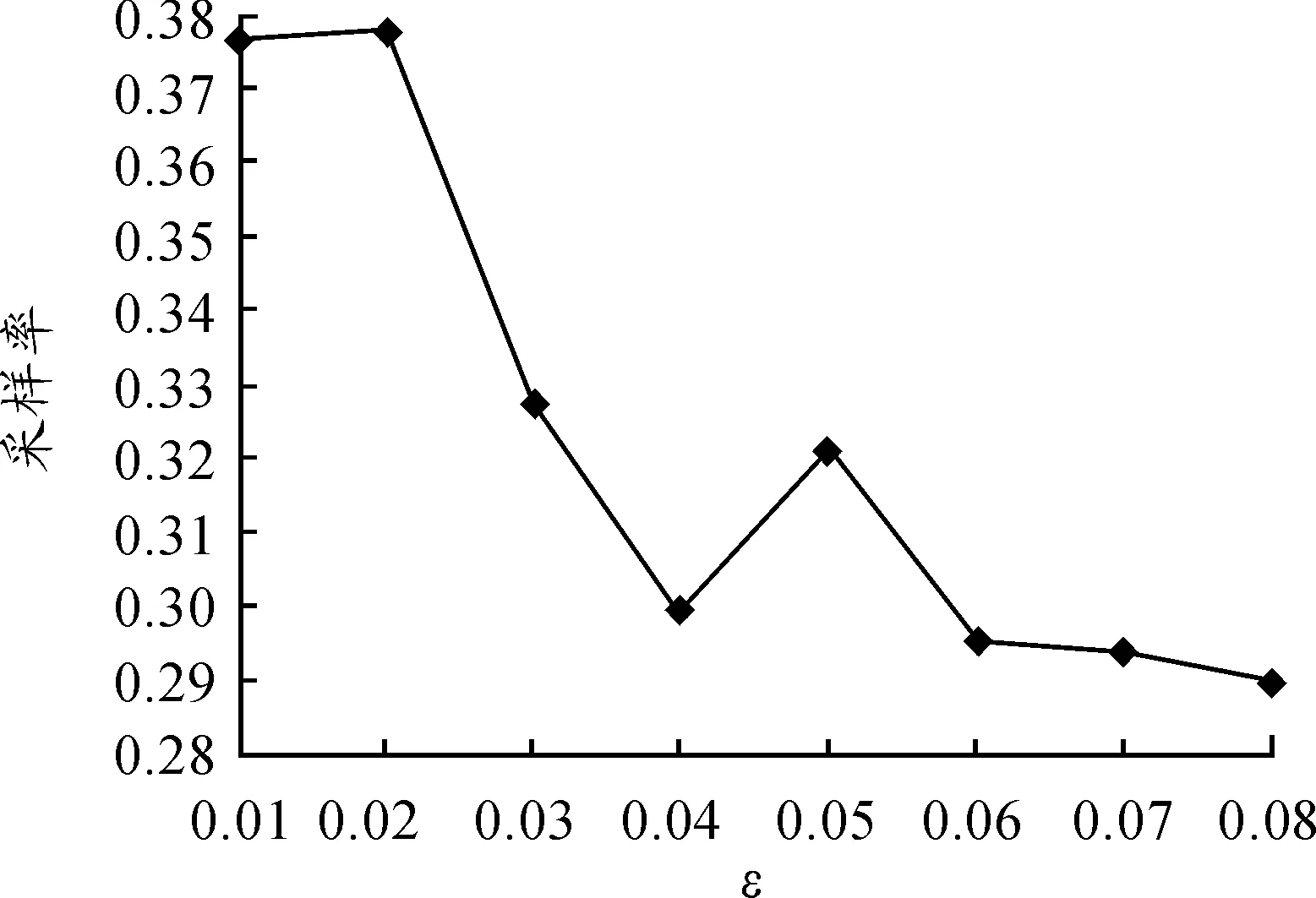
图5 对X2恢复采样率的影响

从图4、5中不难发现：ε越小X2的恢复精度越高，同时对X2的采样率也相应提高。为了调节采样率和准确率之间的平衡，实验观测当ε=0.03时，相对误差只有2.26%，并且采样率只有32.7%，故设置ε=0.03。

3.5 分块大小对实验的影响

为分析分块的粗细粒度对X2恢复的影响，本文采用大小分别为4×4,8×8,16×16,32×32,64×64的分块去运行采样算法，得到的结果如图6、7所示。从图6、7可以发现：分块的大小对最终的采样率和恢复精度影响都不大，故本文最终采用分块的大小为8×8。

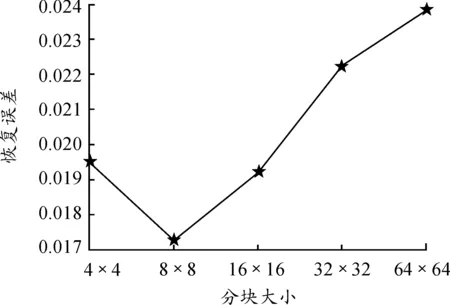
图6 分块大小对X2恢复误差的影响

图7 分块大小对X2恢复采样率的影响

4 结束语

为了降低传感器网络中数据的监测成本，本文利用历史数据极大地降低了采样率和提高了恢复准确率；使用了采样终止条件解决了矩阵秩的未知的难题。此外，本文采用了分块的技术解决了冗余信息集中的问题。冗余信息集中在一起，无须全部采样，只需采样部分即可准确恢复周围全部数据，这样进一步降低了采样率，提高了系统对数据采样的效率。

[1] YICK J,MUKHERJEE B,GHOSAL D.Wireless sensor network survey[J].Computer Networks,2008,52(12):2292-2330.

[2] ARORA A,RAMNATH R,ERTIN E,et al.Exscal:Elements of an extreme scale wireless sensor network[C]//11th IEEE International Conference on Embedded and Real-Time Computing Systems and Applications (RTCSA’05).USA:IEEE,2005:102-108.

[3] LIU Y,MAO X,HE Y,et al.CitySee:Not only a wireless sensor network[J].IEEE Network,2013,27(5):42-47.

[4] ANASTASI G,CONTI M,DI FRANCESCO M,et al.Energy conservation in wireless sensor networks:A survey[J].Ad hoc networks,2009,7(3):537-568.

[5] LUO C,WU F,SUN J,et al.Compressive data gathering for large-scale wireless sensor networks[C]//Proceedings of the 15th annual international conference on Mobile computing and networking.2009:145-156.

[6] WU X,XIONG Y,YANG P,et al.Sparsest random scheduling for compressive data gathering in wireless sensor networks[J].IEEE Transactions on Wireless Communications,2014,13(10):5867-5877.

[7] CHENG J,YE Q,JIANG H,et al.STCDG:an efficient data gathering algorithm based on matrix completion for wireless sensor networks[J].IEEE Transactions on Wireless Communications,2013,12(2):850-861.

[8] XIE K,WANG L,WANG X,et al.Sequential and adaptive sampling for matrix completion in network monitoring systems[C]//2015 IEEE Conference on Computer Communications(INFOCOM).USA:IEEE,2015:2443-2451.

[9] WU X,YANG P,JUNG T,et al.Compressive sensing meets unreliable link:sparsest random scheduling for compressive data gathering in lossy WSNs[C]//Proceedings of the 15th ACM international symposium on Mobile ad hoc networking and computing.2014:13-22.

[10]KONG L,XIA M,LIU X Y,et al.Data loss and reconstruction in wireless sensor networks[J].IEEE Transactions on Parallel and Distributed Systems,2014,25(11):2818-2828.

[11]XIE K,NING X,WANG X,et al.Recover Corrupted Data in Sensor Networks:a Matrix Completion Solution[J].IEEE Transactions on Mobile Computing,2017 (99):1434-1448.

[12]WU Xiaopei,LIU Mingyan,WU Yue.In-situ soil moisture sensing:Optimal sensor placement and field estimation[J].TOSN,2012,8(4):33.

[13]WANG J,TANG S,YIN B,et al.Data gathering in wireless sensor networks through intelligent compressive sensing[C]//INFOCOM,2012 Proceedings IEEE.2012:603-611.

[14]LIU Y,HE Y,LI M,et al.Does wireless sensor network scale A measurement study on GreenOrbs[J].IEEE Transactions on Parallel and Distributed Systems,2013,24(10):1983-1993.

[15]GreenOrbs系统[EB/OL].[2016-11-12].http://www.greenorbs.org/

(责任编辑 杨黎丽)

Sampling-Aware Based Accurate Spatial-Temporal Data Completion for Wireless Sensor Networks

CHEN Ye-bin1, WANG Ren-wei1, LI Ying2

(1.College of Computer Science and Technology, Anhui University of Technology, Ma’anshan 243032, China; 2.School of Science and Engineering, Ma’anshan Teacher’s College, Ma’anshan 243041, China)

With the deepening of smart city, the requirements of physical environment sensoring are becoming higher and higher. Wireless sensor networks (WSNs) have been built for continuously collecting environmental data including temperature, humidity, illumination and carbon dioxide etc. Unfortunately, extremely large amount of data transmission hinder the large-scale WSNs long time running. As a newly emerging technique, matrix completion, concerns the recovery of a low-rank matrix from incomplete samples of its entries. Because of the spatial-temporal correlation in sensor data, data from adjacent node in adjacent time slots are redundant, so we use the block sampling strategy for sparse sampling to reduce the data transmission cost.

wireless sensor networks; sparse sampling; matrix completion; sampling strategies

2017-01-16

安徽省教育厅科学研究重大项目 (KJ2015ZD39)

陈业斌(1971—)，男，安徽全椒人，教授，主要从事计算机网络及数据库研究；王仁伟(1991—)，男，安徽天长人，硕士研究生，主要从事无线传感器网络及室内定位研究，E-mail: wangrenweiahut@163.com。

陈业斌， 王仁伟，李颖.无线传感器网络中基于采样的时空数据恢复[J].重庆理工大学学报(自然科学)，2017(6):127-133.

format：CHEN Ye-bin, WANG Ren-wei, LI Ying.Sampling-Aware Based Accurate Spatial-Temporal Data Completion for Wireless Sensor Networks[J].Journal of Chongqing University of Technology(Natural Science)，2017(6):127-133.

10.3969/j.issn.1674-8425(z).2017.06.019

TN929

A

1674-8425(2017)06-0127-07