社交媒介传播的稳态均衡及信息传播抑制策略

张新刚，何万波

（1.黄冈师范学院新闻与传播学院，湖北黄冈438000；2.重庆工商大学财政金融学院，重庆400067）

社交媒介传播的稳态均衡及信息传播抑制策略

张新刚1，何万波2

（1.黄冈师范学院新闻与传播学院，湖北黄冈438000；2.重庆工商大学财政金融学院，重庆400067）

文章以“互联网+”技术下的社交网络为媒体载体，构建了媒介传播的SIR模型，并给出了媒介传播的稳态均衡条件。在此基础上，加入信息传播潜伏者变量，将SIR模型拓展为SEIR模型。拓展的SEIR模型表明，在无法确知信息网络全局结构的情况下，重要熟人免疫策略即可达成对目标信息的免疫作用。

媒介经济学；社交媒介传播；信息传播稳态均衡；传播免疫机制

0 引言

社交媒介（Socialmedia）即社交网络，最早由美国心理学教授Milgram S（1967）[1]提出，并在其六度分隔理论(six degrees of separation)中指出，在社会交往过程中，每一社会个体只需通过6个人就能与任何一个陌生人打交道。这一理论被后来学者又称为“小世界效应理论”。随着“互联网+”的运用，社交媒介已不仅仅止于20世纪70年代的实体社交网络，当下的虚拟社交网络在信息传播过程中已大有可为。在“互联网+”下的社交网络中，巨量信息使得人们难以甄别其真假，信息传播速度也达到了前所未有的程度。于是，“信息爆炸”时代，社交网络的信息传播何时能够达到传播均衡的状态？对于未经证实的信息（比如“不良信息”或“谣言”）如何才能使其“止于智者”？信息传播的抑制策略如何制定与实施？为此，本文拟基于现有文献，构建信息传播的SIR模型及其稳定均衡点方程。并据此引入“潜伏者”变量，将SIR模型拓展成信息传播SIER模型，在此基础上确立重要熟人免疫策略。

1 基于SIR模型的信息传播稳态均衡

1.1 SIR模型与信息传播速率

为了研究信息传播机制，本文假定信息传播载体可处于三种基本状态，相应地，传播节点分别为易感染者（又称健康者）S、感染者I和免疫者R三种。对于特定信息而言，健康者从未接收过此信息本身尚处于“无知”状态；感染者已经接收并处于信息传播状态之中；与健康者相比，免疫者也不传播此信息，但它已经接收过此信息，而且已经做出甄别处理认为此信息无传播价值而不再传播此信息。

接下来，本文做如下设定：（1）感染者I接受信息后，通过信息甄别，认为此信息无传播价值而拒绝传播（即成为免疫者R）的概率为p1；（2）在信息爆炸的当今社会，大多数信息是不经意间在人们眼前流过，使其成为人们“不记得”的信息，即信息会有被遗忘的可能。由于“被遗忘”的存在，使得感染者I和免疫者R又可能成为易感染者S，设其概率分别为p2与p3；（3）接受信息后，健康者S成为免疫者R的概率为p4，成为感染者I的概率为p5。于是，信息传播SIR模型可作如图1表述：

图1 信息传播S|R模型

为了考察信息在社交网络里的传播机制，特用变量(t)、I(t)、R(t)分别表征t时刻社交网络健康者、感染者和免疫者的密度分布，则：

公式（1）的初始状态为（即t=0时）：

于是得到信息传播的平均场方程如下

联立公式（3），得出信息密度：

1.2 信息传播稳态均衡求解

接下来寻求社交网络信息传播的均衡点，即S,I,R能相互转化的信息传播状态，此时S,I,R三节点密度变率为0，结合式（5），得出数理表达式如下：

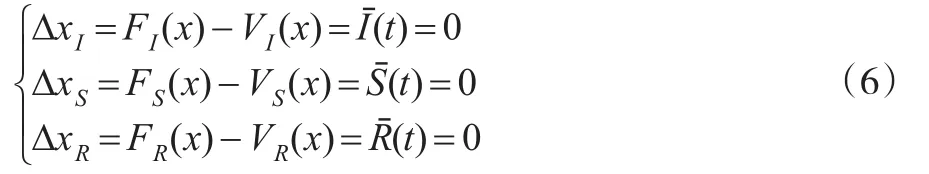
对上式求解，得到两个平衡解X1、X2：

均衡点X1即为初始状态，社交网络处于“无知”状态，无外界信息的传入，此时，对于特定信息而言，所有节点都处于健康状态，即易感染状态；均衡点X2为社交网络的动态平衡状态，信息在此社交网络中，处于稳定传播之中，S, I,R三种节点处于动态平衡之中。

其中,得：

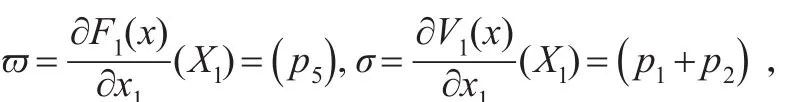
所以，均衡点X1处有：

由式（10），并据劳斯-赫尔维茨(Routh-Hurwitz)稳定性判据可得X1为稳态均衡点[3]。此时，无论社交网络中有多少健康接点，由于没有信息源的存在，感染节点都不复存在。

第二，当Q0＞1时，X1处于非稳态，前已述及，反之亦然。此时将X2代入式(9)，得均衡点X2处的Jacobi矩阵方程如下：

由式（12），并据劳斯-赫尔维茨(Routh-Hurwitz)稳定性判据可得X2为稳态均衡点。此时，社交网络中的节点S,I,R状态均收敛于Y2，在此信息交换过程中，S,I,R节点密度保持动态均衡状态。

因此，得出结论：（1）当Q0＜1时，X1为社交网络信息传播的稳态均衡点；（2）当Q0＞1时，X1为社交网络信息传播的非稳状态点，X2为社交网络信息传播的均衡稳态点，此时，在此信息交换过程中，S,I,R节点密度保持动态均衡。

2 置入潜伏者变量的信息传播SEIR模型

在上述SIR信息传播模型中，本文设定了信息传播节点的三种基本状态：易感染者（又称健康者）S、感染者I和免疫者R。并且设定：健康者处于“无知”状态，感染者正处于接收并传播信息状态之中；免疫者已经接收但不再传播信息。接下来，本文在上述三种状态的基础上，再引入潜伏者E变量。并假定：（1）潜伏者是信息的潜在传播者，它接收过此信息，由于“遗忘机制”的存在，它暂时没有传播此信息，但也没有获得免疫，后续再次接收此信息，可能再次成为感染者I或免疫者R；（2）潜伏者E再次接收此信息后，转变成感染者I的概率设定为p7，转变成免疫者R的概率设定为p8；健康者S接收信息后，转变成潜伏者E的概率设定为p6；已经“潜伏”过的免疫者转变成感染者I的概率设定为p9。于是，原来的SIR信息传播模型就可以拓展为下述SIER模型，如图2所示。

图2 信息传播S|ER模型

令t时刻社交网络中的节点数量为N，此时，式（1）就转换为：

S(t)+I(t)+E(t)+R(t)=N，(0≤pi≤1)，∀i=1，...，9(13)

其中，S(t),E(t),I(t),R(t)分别为四种节点的密度（以数量表征），此时，以偏微分表述的信息传播平均场方程变成如下式：

式（14）中第一子式表示信息传播过程中健康者S的变化率；第二子式表示信息传播过程中感染者I的变化率；第三子式表示信息传播过程中潜伏者E的变化率；第四子式表示信息传播过程中免疫者R的变化率。

考察现有相关文献[5],根据上述SIER模型的信息传播平均场方程，再结合前述信息传播的稳态均衡模型，绘制出了信息传播的仿真模型，如图3所示。

图3 基于社交网络的信息传播仿真模型图

从图3可得出：健康节点S(t)从初始时间（t=0）起，即随社交网络中感染者I(t)和潜伏者E(t)的增加而减少,且其衰减速率逐渐趋缓至0；而感染者I(t)和潜伏者E(t)从初始时间（t=0）起就迅速递增，至时间t=1时，其数量达到最大值而逐渐趋减，速率至0，数量也最终趋向0；免疫者R(t)从初始时间（t=0）起一路迅速增长，最终（t=tM）增加速率趋缓，数量趋向于最大值N（此时潜伏者E(t)也不再“潜伏”，再次接收信息后，变成免疫者）,即所有社交网络用户基本已经“免疫”，信息不再“肆虐”传播，信息传播趋向均衡态，即达到上述的X2均衡点，信息传播的“基本再生参数”Q0＞1，此时的S,I,R节点密度保持动态均衡。

3 社交网络信息传播的抑制策略

由上文可知，潜伏者E(t)也是影响社交网络信息传播的重要变量，但是，潜伏者再次接收信息后，既有转变成感染者I(t)的可能，也有转变成免疫者R(t)的可能。也就是说，潜伏者E(t)的后续转变状态是“不定”的，没有方向性。而且从图2可知，潜伏者E(t)后续“连通”感染者I(t)或免疫者R(t)。为此，接下来本文结合社交网络拓扑结构特性，运用无权无向网络图G（如图4所示）对社交网络信息（主要是不良信息，如“谣言”等）传播的抑制策略进行构建。

图4 社交网络信息传播的无权无向网络图G

在社交网络信息传播的无权无向网络图G中，“边”与“边”的连通“无向”，点与点之间的线“无权”，即能连通，距离为1（不相通则距离为0）。在下文中，要求构建社交网络的免疫策略，即为指定一选取的节点1作为初始节点，要求寻求从1出发到网络图G中的其他节点i的最短路径d，即为节点1到其他节点i进行免疫的被控制程度。基于此原理，构建以下社交网络信息传播的抑制策略：

步骤3：通过执行步骤2后，根据关系的重要性程度给节点Si建立一个关系群，即子网络Gi，并判定其是否连通。若Gi连通，则计算子网络Gi所有节点与Si的关系，并按其重要性大小进行排序。

步骤4：将步骤3中子网络Gi中的关系重要性大小分成一般熟人关系和重要熟人关系等两组，分别记为,此时数组；

步骤5：对i=i+1进行测算，重复运行上述步骤1至步骤4，计算出d值，并得出数组，即为社交网络G中易感染节点Si的社交关系群。然后考虑各关系者对Si的影响程度，实施信息矫正，最终使“谣言止于智者”，不良信息传播得以抑制。

利用图4，不少文献提出了诸多不良信息的抑制策略，如顾亦然,夏玲玲（2012）[5]就以社交网络Facebook为研究对象，对目标免疫、熟人免疫和重要熟人免疫策略做出过研究。研究结果显示，重要熟人免疫策略较目标免疫更具优势。因为相对于目标免疫策略，重要熟人免疫策略只需选定考察节点的最重要关系群及其个体（上所述Gi中的g2及其成员），而无须详细掌握社交网络拓扑结构值全貌。本文认为，在社交网络信息传播实践中，任一社会个体都有其特定的“朋友圈”，其中定有关系最密切或关系最重要的人。为此，对某一特定信息，针对特定社交网络中的某一特定社会成员或某一特定群体，进行信息引导，可寻求其关系最重要的人或最可靠的人予以实施。这种重要熟人免疫策略将能起到路径畅、成本低、效率高的效果。

4 结论

本文通过对社交媒介传播进行分析，研究信息传播机制，借鉴传染病模型理论构建社交网络信息传播的SIR模型，加入信息传播潜伏者变量，将SIR模型拓展为SEIR模型。分析得出在无法确定信息网络全局的情况下，重要熟人免疫策略可实现对目标信息的免疫作用，由此得出以下结论：

（1）对社交网络传播机理进行分析，设定信息传播载体的传播节点，分别为易感染者（又称健康者）、感染者和免疫者三种，介绍传染者、健康者、免疫者之间的密度分布，基于传播速率建立信息传播SIR模型。通过模型分析的结果显示，熟人免疫策略能很好达成对目标信息的免疫作用。

（2）寻求社交网络信息传播的均衡点，当信息传播的“基本再生参数”小于1时，初始状态为社交网络的信息传播稳态均衡点；当信息传播的“基本再生参数”大于1时，初始状态为社交网络的信息传播的非稳状态点，社交网络的动态平衡状态为社交网络信息传播的均衡稳态点，在此信息交换过程中，传染者、健康者、免疫者三者节点密度保持动态均衡。

（3）结合社交网络拓扑结构特性，运用无权无向网络图可以得到诸多不良信息的抑制策略，其中重要熟人免疫策略较目标免疫更具优势。在针对社交网络的特定对象进行信息引导时，可通过与其关系最重要的人来进行具体实施，且能取得较好的效果。

[1]Milgram S.Behavioral Study of Obedience[J].Journal of Abnormal and Social Psychology,1967,67,(4).

[2]Van den Driessche P,Watmough.J.Reproduction Numbers and Subthreshold Endemic Equilibria of Compartmental Models for Disease Transmission[J].MathBiosci,2002,(180).

[3]谢彦麟.用Euclid序列解Routh-Hurwitz问题与判定驻定组稳定性[J].华南师范大学学报:自然科学版,1986,(1).

[4]Wang Y B,Xiao G X,Liu J.Dynamics of Competing Ideas in Complex Social Systems[J].New Journal of Physics,2012,14,(1).

[5]顾亦然,夏玲玲.在线社交网络中谣言的传播与抑制[J].物理学报, 2012,61(23).

（责任编辑/刘柳青）

G206.2

A

1002-6487（2017）11-0045-04

教育部人文社会科学研究青年项目（14YJC860002）；重庆市社会科学规划项目（2016BS012）

张新刚（1980—），男，黑龙江哈尔滨人，硕士，讲师，研究方向：媒介经济与理论。何万波（1965—），男，四川广安人，副教授，研究方向：互联网财税理论与政策。