一种分数阶微积分算子的有理函数逼近阶数最小化方法
2017-07-05张旭秀李卫东盛虎丁鸣艳
张旭秀, 李卫东, 盛虎, 丁鸣艳
(大连交通大学 电气信息学院,辽宁 大连 116028)
一种分数阶微积分算子的有理函数逼近阶数最小化方法
张旭秀, 李卫东, 盛虎, 丁鸣艳
(大连交通大学 电气信息学院,辽宁 大连 116028)
针对分数阶微积分算子的实现问题,基于对数幅频特性,导出分数阶积分算子1/sγ(0<γ<1)的一种有理函数逼近公式,该式与Manabe提出的公式类似,但比它更便于分析和应用,讨论了该式应用范围的拓展。为了改善相位逼近精度,提出有理函数构建频率区间概念,它包含逼近频率区间。在满足逼近精度和逼近频率区间条件下,提出使有理函数阶数最小化的两点措施:①充分利用对数幅频特性渐近线与准确曲线之差,适当加宽分数阶积分算子与有理函数二者对数幅频特性之间的误差带;②根据逼近频率区间,合理选择函数构建频率区间。计算实例表明上述工作的有效性。
分数阶微积分算子;有理函数逼近;Manabe近似式;有理函数阶数最小化;应用范围拓展
0 引 言
分数阶微积分算子的实现方法,分为频域滤波器法(连续模型法)和数字滤波器法(离散模型法)两大类。连续模型法是用s的有理函数去逼近分数阶微积分算子,离散模型法是用z传递函数去逼近分数阶微积分算子。本文研究内容属于连续模型法。现有的一些连续模型法,如分段逼近连分式展开法、Matsuda连分式展开法、Carlson法、Oustloup法及其改进方法[1-2],它们的共同特点是不能预先准确设置逼近误差,这可能导致生成的有理函数阶数偏高。
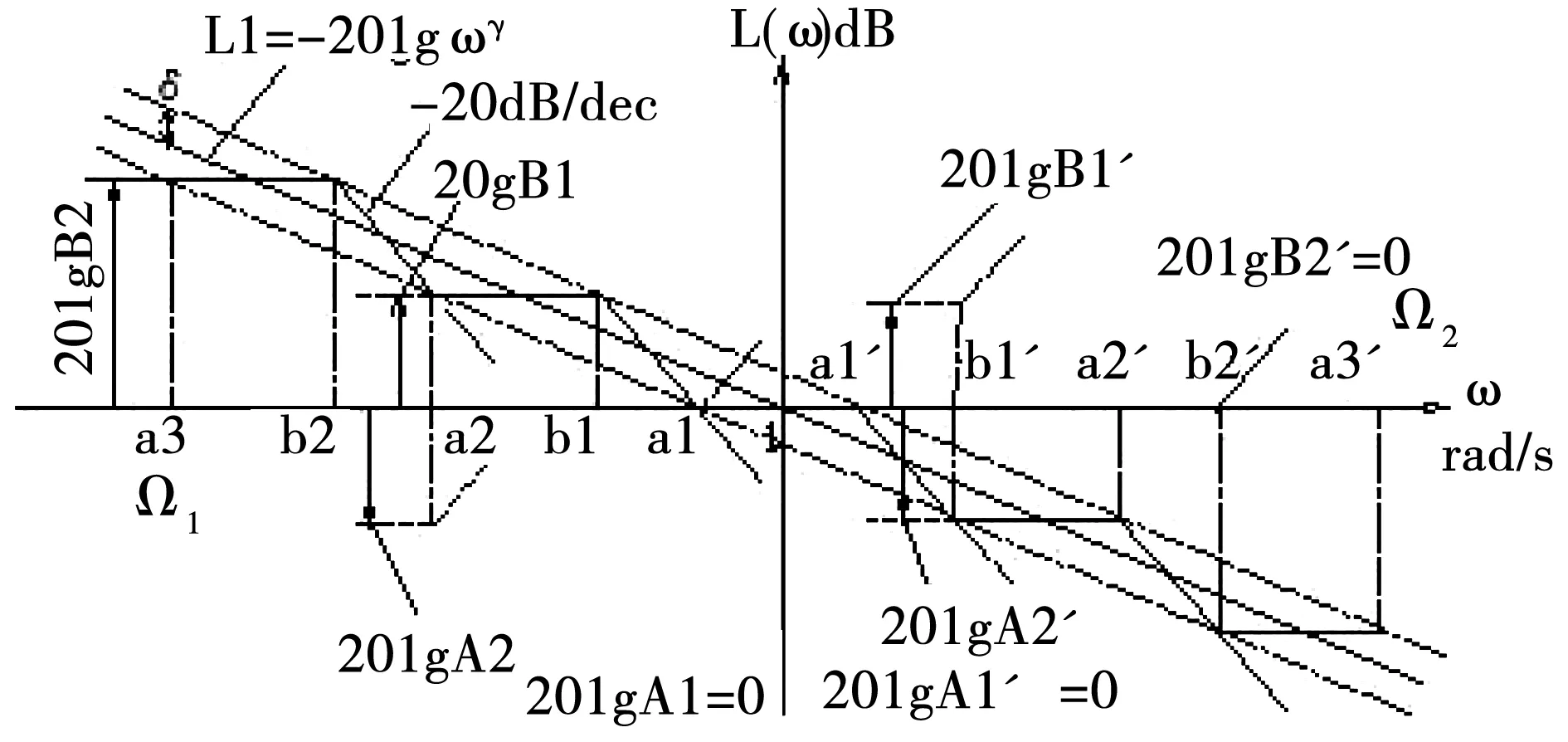
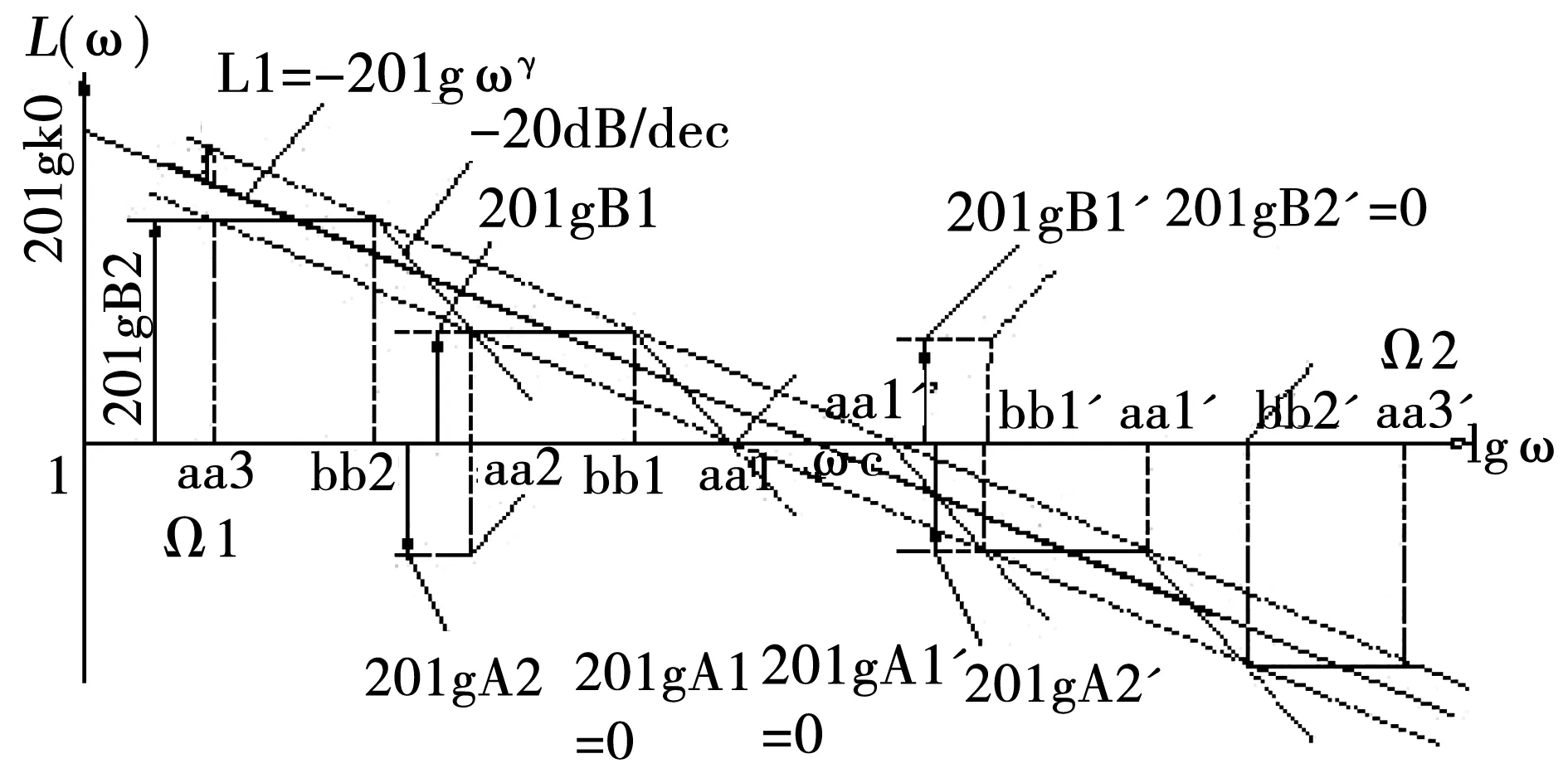
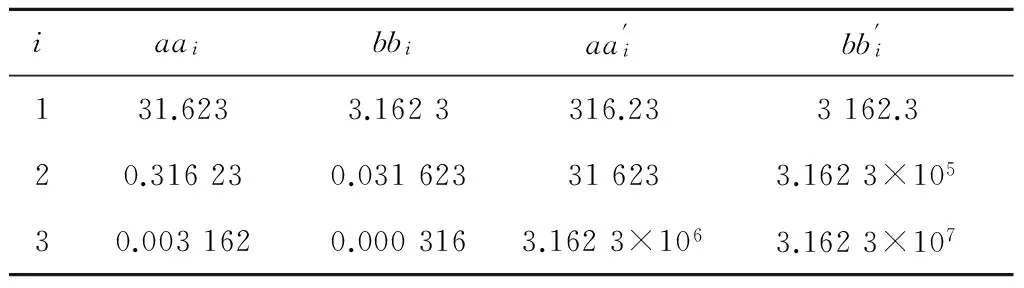
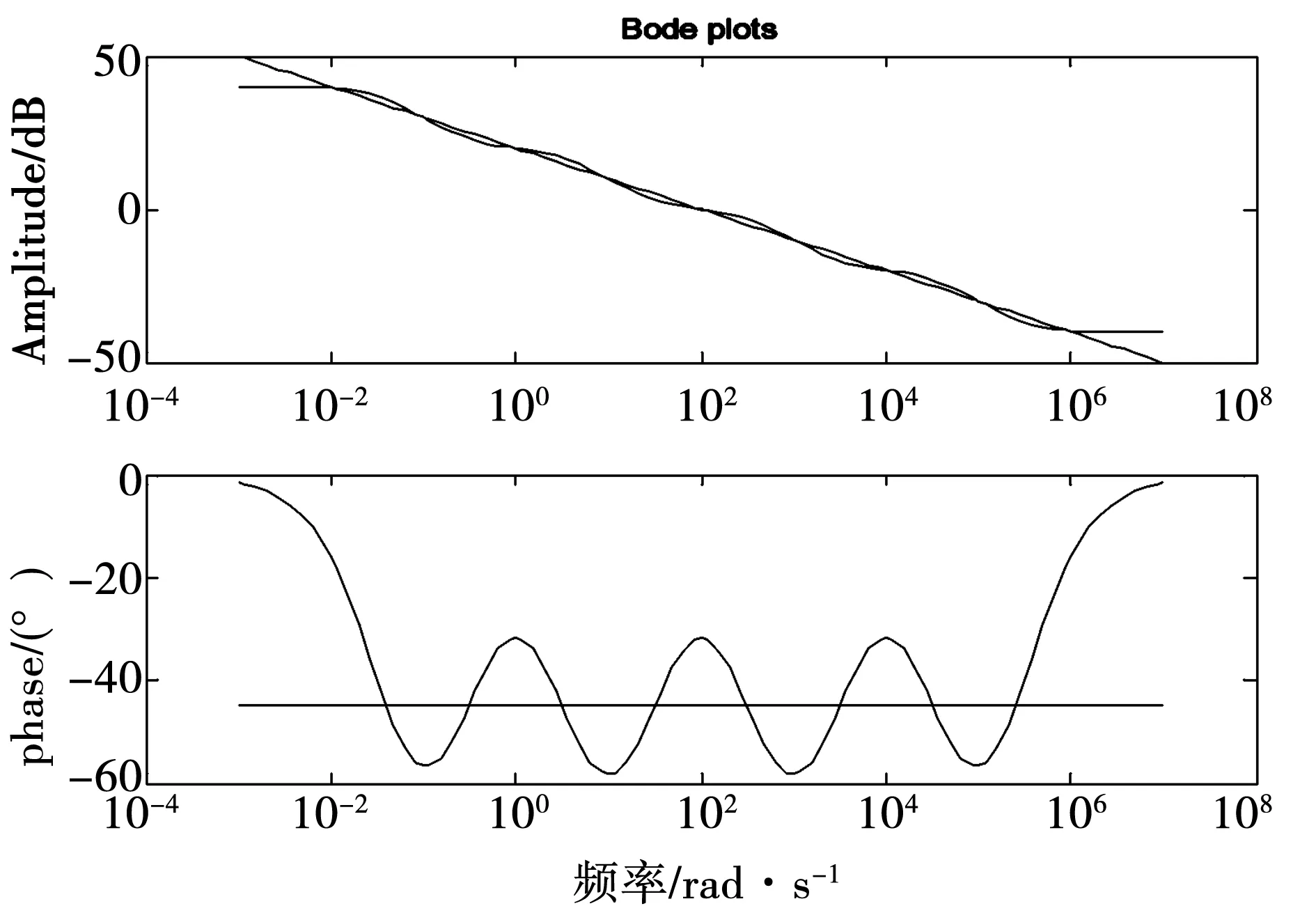
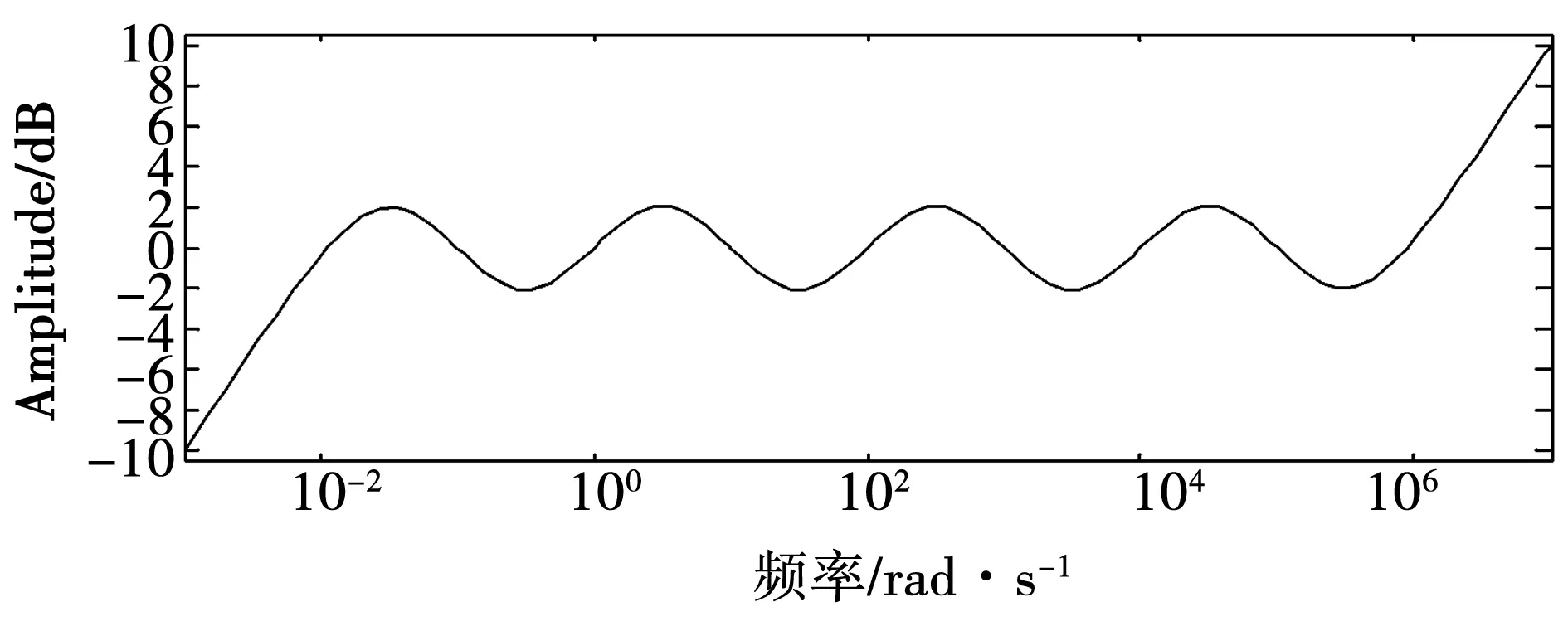
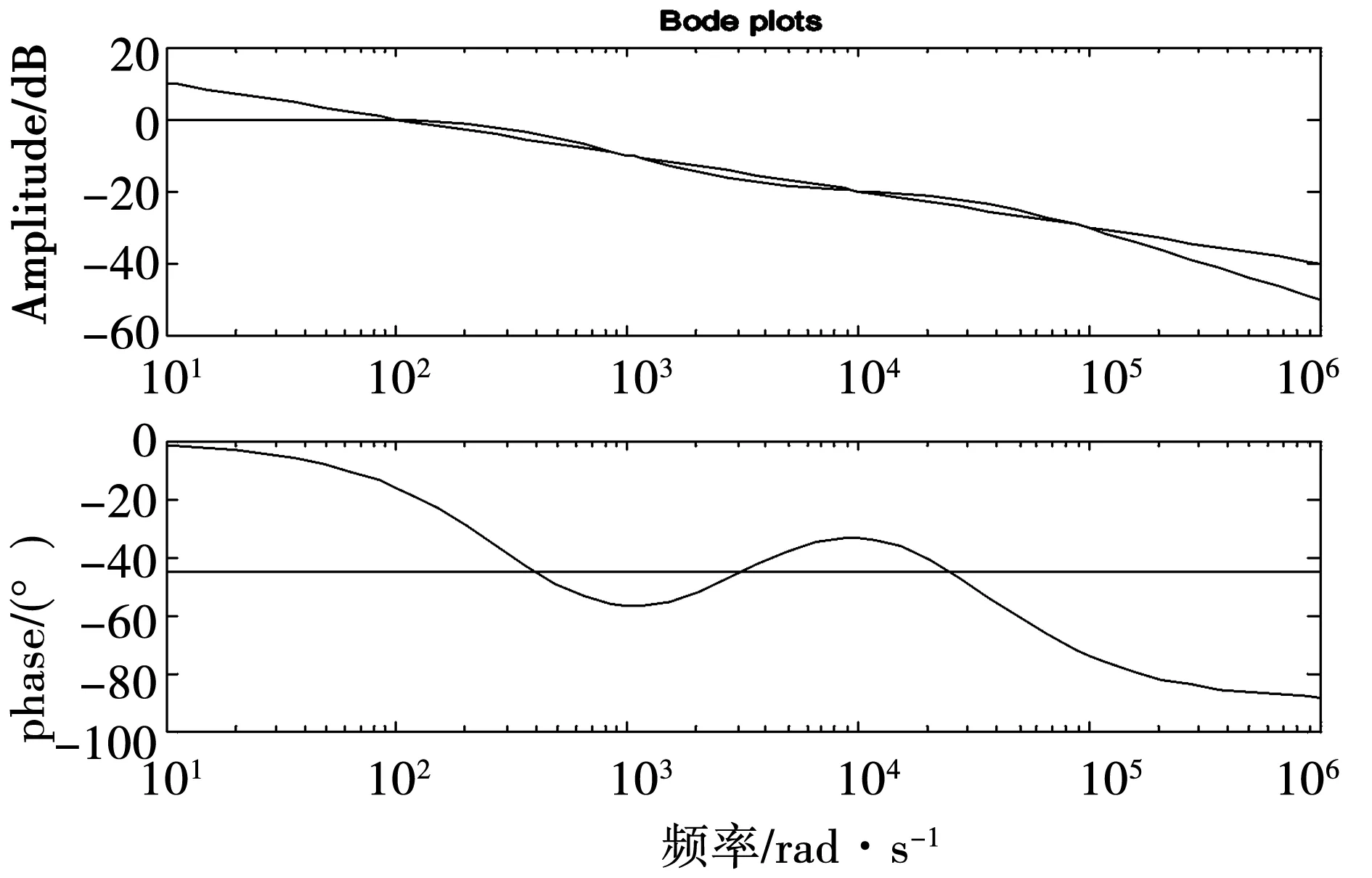
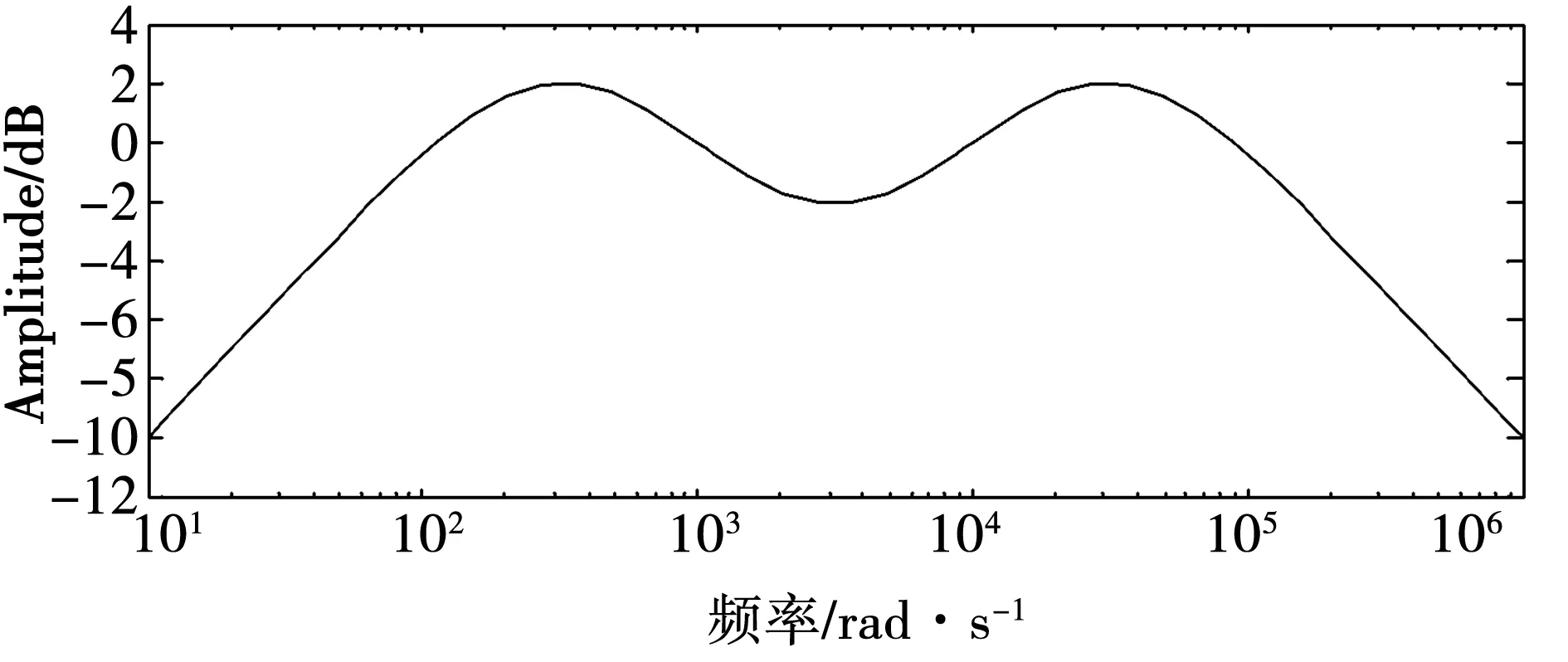
Manabe提出一种基于Bode图的有理函数逼近方法[3-4],克服了上述局限性,其做法是:在Bode图的对数幅频坐标平面中,绘出分数阶积分算子的对数幅频率特性 ,这是一条斜线,以这条斜线为基础,根据对幅度逼近误差的要求,设置一定宽度的误差带,在误差带内用两种具有典型斜率(-20dB/dec,-40dB/dec)的线段交替连接组成折线,来逼近分数阶积分算子1/sq(0 为克服以上两种基于Bode图的有理函数逼近方法存在的问题,本文采用另一种方法导出分数阶积分算子1/sγ(0<γ<1)的有理函数逼近公式,以该式为基础,拓展它的应用范围。为改善相位逼近精度,提出有理函数‘构建频率区间’概念,所要求的‘逼近频率’区间在‘构建频率区间’内部。在满足逼近频率区间和逼近精度(最大幅度逼近误差)要求条件下,采取以下两种措施实现有理函数阶数最小化:1)考虑到用渐近线表示的对数幅频率特性与实际曲线之差,适当放宽逼近误差带;2)根据逼近频率区间,更精细地选择构建频率区间。 Manabe法在Bode图的指定频域[Ω1,Ω2]内,用整数阶有理函数R(s)的对数幅频特性(折线)逼近分数阶积分算子1/sq(0 1.1 交接频率计算 图1 ωc=1时的Bode图Fig.1 Bode when ωc=1 经简单推导,左侧交接频率有 (1) (2) 右侧的交接频率通式 (3) (4) 1.2 逼近有理函数的生成 首先构建纵轴左侧对数幅频特性对应的逼近函数RL(s),自纵轴向左依次列出各环节传递函数,取它们的连乘积,在Bode图中20lgA1=0,20lgA2=-20lgB1,表明环节系数A1=1,A2与B1互为倒数,故有 假设直到Ω1=aj+1,共有j对环节,则上式可推广为一般形式 (5) Ω1=aj+1。 (6) 假设纵轴右侧直到Ω2为止,对数幅频特性对应的环节共有k对,则上式可推广为一般形式 (7) (8) 左右两侧对应的逼近函数连乘,便得整个折线对应的逼近函数,即1/sγ的逼近有理函数 (9) 该式对应的函数构建频率区间下、上限分别为 Ω1=aj+1, (10) Ω2=1/ak+1。 (11) 式(9)与Manabe逼近函数公式乘以算子s的结果相同。但二者的区别是,Manabe法把[Ω1,Ω2]就当作逼近频率区间,而式(9)的逼近频率区间是[ωa,ωb],按上述,它是在[Ω1,Ω2]内部。 下面以式(9)为基础,研究有理函数阶数最小化以及应用范围拓展问题。 由图1可见,在逼近频率区间一定的前提下,误差带越宽,则有理函数的环节数越少,阶数越低。为了降低有理函数的阶数,应当在满足逼近误差条件下,尽量加宽误差带。为此,需要考虑以下两个问题:第一,有理函数的对数幅频特性渐近线与准确曲线之间的误差。第二,对数幅频特性逼近误差曲线极点频率与其邻近的交接频率的关系。 2.1 对数幅频特性渐进线与准确特性之间的误差 在Bode图中,逼近函数的对数幅频特性是用渐进线表示的。对数幅频特性渐进线与准确特性之间存在误差,交接频率处,误差最大。惯性环节的此误差为(渐进线值减准确值)3dB;对于一阶微分环节,此误差为-3dB。 用渐近线表示的对数幅频特性(折线)总是在准确特性曲线的外侧,因此,如果直接按幅频特性逼近误差的最大允许值(折算成对数幅频特性相应值)设置误差带宽(单侧)δ,那么,误差带宽偏窄,求得的R(s),其阶数偏高,实际逼近误差小于设定值,即逼近精度尚有裕量。消除这个裕量,可能换取R(s)阶数的降低。为此,应适当加宽误差带。加宽多少为宜将在2.3节回答。 2.2 逼近误差曲线极点频率与交接频率的关系 (12) 逼近误差带宽度的设置 假设要求幅度逼近的最大允许误差为μ,在Bode图中为 δ0=20lgμ。 (13) Bode图中的误差带宽度(单边)δ应当在δ0基础上,增加一个修正量Δδ, δ=δ0+Δδ。 (14) 其中δ是逼近函数对数幅频特性渐近线在ωj处与分数阶积分算子对数幅频特性之差,δ0是逼近函数对数幅频特性准确值在ω*处与分数阶积分算子对数幅频特性之差。Δδ的取值同ω*与ωj的相对大小有关,具体分以下三种情况: 图2 Δδ的选取Fig.2 Selecting of Δδ Δδ=3 dB。 (15) Δδ=δ-δ0<3 dB。 (16) Δδ=δ-δ0<3 dB。 (17) γ值偏离0.5越远,则Δδ应越小。此时的Δδ值不能用解析方法求出,只能根据经验或者试探选取,例如γ=0.4和γ=0.6 时,可以取Δδ≈2.8 dB,γ=0.2和γ=0.8时,可以取Δδ≈2 dB,等等。 基于上述,在计算交接频率之前,应当按以下步骤计算α: 1)根据设定的幅频特性最大允许逼近误差α0,计算δ0=20lgα0,或者直接设定δ0; 2)根据γ,选取Δδ,计算δ=δ0+Δδ; 3)计算α=10δ/20。 式(9)的阶数可以拓展用于以下几种情况: 3.1 积分算子阶数的拓展 式(9)的阶数可以拓展用于以下几种情况: 1)用于逼近 1/sq,(n 2) 用于对微分算子sβ,(0<β<1)的逼近:先按式(9)求出1/sβ的逼近有理函数R(s),然后取R(s)的倒数即可。 3)用于逼近微分算子sp,(n 3.2 积分算子系数的拓展 设要逼近的传递函数为G0(s)=k0/sγ,k0>1,0<γ<1,要求逼近频率区间为[ωa,ωb],求G0(s)的逼近有理函数R(s)。 与图1对照可见,图3中的对数幅频特性,是图1中的对数幅频特性沿着横轴右移lgωc的结果。修改图1中的交接频率公式,得到图3的交接频率。有 aai=aiωc,i=1,2,3,…, (18) bbi=biωc, (19) (20) (21) 图3 公式(9)拓展到ωc>1时Bode图Fig.3 Bodewhen equation (9) expanding to ωc>1 最后,得到G0(s)=k0/sγ的逼近有理函数表达式 (22) 相应地,函数构建频率下、上限分别改为 Ω1=aaj+1=aj+1ωc,bbj≤ωb (23) (24) 前面给出的逼近有理函数,其分子与分母阶数都是相等的。在一定条件下,可以突破这种限制,使逼近有理函数阶数降低一阶。以右侧为例,参看图1,把式(7)和式(8)重写如下 (25) (26) (27) (28) 仅当ωb在式(27)所示范围内时,必须使用式(25)和式(26);当ωb在式(28)所示范围内时,除了可以使用式(25)和式(26)以外,还可以取 (29) (30) 类似地,把式(5)RL(s)的导出过程及其一般形式重写如下: (31) (32) 式(32)第二式是参照式(31)(j=2)写出的。 前面已指出,当ωa满足条件bj≤ωa Ω1=aj+1。 (33) ωa的浮动范围也可以分成两段: bj≤ωa (34) aj≤ωa (35) 仅当式(34)成立时,才必须使用式(32)和式(33),当式(35)成立时,除了可以使用式(32)和式(33)以外,为节省一个惯性环节,还可以取 Ω1=bj。 (36) 并把式(32)修改成 (37) 从Bode图1来看,与式(32)及式(33)对应,折线从Ω1=a3对应的水平线的左端进入误差带;与式(36)及(37)对应,折线从Ω1=b2对应的斜线的上方进入误差带。 上述有理函数降阶的思想,同样可以用于ωc>1的情况。 综合上述,本文所给出方法的实现过程如下: 1)题设条件,包括要逼近的微积分算子,逼近频率区间[ωa,ωb],对数幅频特性最大逼近误差δ0或者幅频特性最大逼近误差α0; 2)把要逼近的微积分算子,转换成逼近1/sγ的问题; 3)根据γ确定Δδ,进一步求出误差带宽(单边)δ; 4)计算交接频率:如果ωc=1,则按公式(1)、式(2)、式(3)、式(4)进行;如果ωc>1则按公式(18)、式(19)、式(20)、式(21)进行。以上公式都是递推公式,可以取i=1,2,3,… 5)确定构建频率区间和有理函数表达式 对于ωc=1,有以下4种情况: 1)如果ωa满足不等式bj≤ωa Ω1=aj+1, (38) (39) 2)如果满足aj≤ωa Ω1=bj, (40) (41) (42) (43) (44) (45) 根据ωa和ωb的实际位置,从情况1)和2)中取出一个逼近函数,从情况3)和4)中取出一个逼近函数,两个逼近函数连乘,得到1/sγ的逼近有理函数R(s)。 实例1:求10/s0.5的逼近有理函数,逼近频率区间[0.05,1.5×105](rad/s),对数幅频特性(准确值)逼近误差不大于2dB,即幅频特性逼近误差不大于α0=102/20=100.1=1.26。 (46) 10/s0.5及其逼近函数式(46)的对数幅频特性和相频特性曲线如图4所示,对数幅频特性的逼近误差曲线如图5所示。 图4 10/s0.5及其逼近函数的对数幅频特性和相频特性Fig.4 Logarithmic amplitude frequency and phase frequency characteristics of 10/s0.5and approximation function 图5 对数幅频特性的逼近误差曲线Fig.5 Approximation error curve of logarithmic amplitude frequency characteristics 实例2:逼近区间为[3×102,3×105](rad/s), 其他同实例1。 解:ωa=3.16×102>ωc=102,所以只需使用图1右侧的幅频特性,按表1,它对应的逼近有理函数为 (47) 10/s0.5及其逼近函数式(47)的对数幅频特性和相频特性曲线如图6所示,对数幅频特性的逼近误差曲线如图7所示。 图6 10/s0.5及其逼近函数的对数幅频特性和相频特性Fig.6 Logarithmic amplitude frequency and phase frequency characteristics of 10/s0.5and approximation function 实例3:逼近频率区间[3×102,3×104],其他同实例2。 (48) 10/s0.5及其逼近函数式(48)的对数幅频特性和相频特性曲线如图8所示,对数幅频特性的逼近误差曲线如图9所示。 图7 对数幅频特性的逼近误差曲线Fig.7 Approximation error curve of logarithmic amplitude frequency characteristics 图8 10/s0.5及其逼近函数的对数幅频特性和相频特性Fig.8 Logarithmic amplitude frequency and phase frequency characteristics of 10/s0.5and approximation function 图9 对数幅频特性的逼近误差曲线Fig.9 Approximation error curve of logarithmic amplitude frequency characteristics 本文基于Bode图,导出一种分数阶积分算子1/sγ,(0<γ<1) 的逼近有理函数公式,它式与Manabe提出的公式类似,但比它更便于分析和拓展。以该式为基础,讨论该式应用范围的拓展提出函数构建频率区间概念,它有别于逼近频率区间;讨论该式应用范围的拓展问题;提出使逼近有理函数阶数最小化的两点措施:第一,根据γ值,给Bode图中的误差带宽增加一个修正量,第二,根据要求的逼近频率区间,精细选择函数构建频率区间,以便在可能情况下,突破有理函数分子分母阶数相等的限制,实现降阶。计算实例表明上述做法是有效的。 [1] 潘金文,彭程,王珍,等,分数阶微分算子的最优有理逼近算法[J], 信息与控制,2014,43(5):518-523. PAN Jinwen, PENG Cheng, WANG Zhen, et al. An optima rational approximation algorithm for a fractional order differential operator[J]. Information and Control,2014,43(5):518-523. [2] 李远禄. 分数阶微积分滤波原理、应用及分数阶系统辨识[D].南京:南京航空航天大学,2007:17-23. [3] Kouyou Sawai, Takahiro Takamatisu and Hiromitsu Ohmori.Adaptive control law using fractional calculus systems[C]//SICE Annual Conference 2012. August 20-23, 2012, Akita University, Akita, Japan. [4] J.A. Tenreiro Machado.Application of fractional calculus in engineering sciences[C]//ICCC2008. IEEE 6th International Conference on Computational Cybemetics,November 27-29,2008. Stara Lesna, Slovakia. [5] 李文,赵慧敏. 一种分数阶微积分算子的有理函数逼近方法.自动化学报[J],2011,37(8):999-1005. LI Wen, ZHAO Huimin. Rational function approximation for fractional order differential and integral operators[J]. Acta Automatica Sinica, 2011,37(8):999-1005. [6] 赵慧敏, 李文, 邓武. 一类分数阶滤波器逼近阶次的选择[J]. 电机与控制学报, 2010, 14(1):90-94. ZHAO Huimin, LI Wen, DENG Wu,Approximation degree selection for one kind of fractional-order filter[J]. Electric Machines and Control, 2010, 14(1): 90-94. [7] 蒲亦非, 王卫星. 数字图像的分数阶微分掩膜及数值运算规则[J],自动化学报, 2007, 33(11): 1128-1135. PU Yifei, WANG Weixing. Fractional differential masks of digital image and their numerical implementation algorithms[J]. Acta Automatica Sinica, 2007, 33(11): 1128-1135. [8] 董俊,张广军,姚宏,等。异结构的分数阶超混沌系统函数投影同步及参数辨识[J], 电子与信息学报,2013,35(6):1372-1375. DONG Jun, ZHANG Guangjun, YAO Hong, et al. Function projective synchronization and parameter identification of different fractional-order hyper-chaotic systems[J]. Journal of Electronics & Information Technology, 2013,35(6):1372-1375. [9] 陈炳文,王文伟,秦前清,基于分数阶积分算子的红外弱小目标检测[J].控制与决策,2012,27(1):147-151. CHEN Bingwen,WANG Wenwei,QIN Qianqing.Infrared dim target detection based on fractional integral operator[J].Control and Decision,2012,29(1):147-151. [10] 李远禄, 于盛林. 非整数阶系统的频域辨识法[J]. 自动化学报, 2007,33(8): 882-884. LI YuanLu, YU ShengLin. Identication of non-integer order systems in frequency domain[J]. Acta Automatica Sinica, 2007,33(8): 882-884. [11] 何春,叶永强,姜斌,等。一种基于分数阶次微积分模板的新型边缘检测方法[J],自动化学报,2012,38(5):776-787. HEChun,YE Yongqiang, JIANG Bin, et al. A novel edge detection method based on Fractional-order Calculus mask[J].Acta Automatica Sinica,2012,38(5):776-787. [12] Li M.Approximating ideal filters by systems of fractional order[J].Computational and mathematical methods in medicine, 2012:ID 365054. [13] LIAO Z, PENG C, LI W, et al. Robust stability analysis for a class of fractional order systems with uncertain parameters[J]. Journal of the Franklin Institute, 2011,348(6):1101-1113. [14] LI W, PENG C, WANGY. Frequncy domain subspace identification of commensurate fractional order input time delay systems[J].Internatiional Journal of Control , Automation and Systems,2011,9(2):310-316. [15] LI Changpin, ZHAO Zhengang, CHEN Yangquan. Numerical approximation of nonlinear fractional differential equations with subdiffusion and superdiffusion[J]. Computers & Mathematics with Applications, 2011,62(3), 855-875. [16] 谭程,梁志珊,张举丘. 电感电流伪连续模式下分数阶Boost变换器的非线性控制[J],物理学报,2014,63(20):1-6. TAN Cheng, LIANG Zhishan, ZHANG Juqiu. Non-linear control for the fractional boost converter in pseudo continuous conduction mode[J],Acta Phys.Sin,2014,63(20):1-6. [17] 周星德,吴利平,曾鹏,等。高速列车引起地基振动分数阶模型[J],振动与冲击, 2014,33(10):34-37. ZHOU Xingde, WU Liping, ZENG Peng, et al. A fractional derivative model for highspeed train-induced ground vibration[J], Journal of Vibration and Shock, 2014,33(10):34-37. [18] 孙会来,金纯,张文明,等。基于分数阶微积分的油气悬架建模与试验分析[J].振动与冲击,2014,33(17):167-172,190. SUN Huilai, JIN Chun, ZHANG Wenming,et al. Modeling and tests for a hydro-pneumatic suspension based on fractional calculus[J],Journal of Vibration and Shock, 2014,33(17):167-172,190. (编辑:刘素菊) Minimum method of rational function orders for approximation fractional differential and integral operators ZHANG Xu-xiu, LI Wei-dong, SHENG Hu, DING Ming-yan (School of Electronics and Information Engineering, Dalian Jiaotong University,Dalian 116028, China) Aiming at the problem of implementation of fractional differential and integral operators, an rational function approximation formula for 1/sγ(0<γ<1)is derived based on logarithmic frequency characteristic. The formula is similar to the Manabe formula,but is more convinient for analysis and application.Its extension of application scope was discussed. In order to improve the accuracy of phase approximation, a rational function constructing the frequency interval is proposed. It contained the approximation frequency interval. To meet the conditions of approximation accuracy and frequency interval approximation, two measures to minimize rational function orders was presented:firtly,make full use of the error between the asymptote and the actual value of the logarithm amplitude- frequency characteristic,and appropriately broaden the error strip of the logarithm amplitude- frequency characteristic of the fractional integral operator vs the rational function;secondly,select the rational function formation frequency area reasonably based on the approximation of the frequency interval. Computation examples show that above work is valid. fractional differential and integral operator; rational function approximation; Manabe- approximation formula; minimum of rational function orders;extension of application scope 2015-12-30 国家科技支撑计划(2015BAF20B02);国家自然科学基金(61471080,No.61201419);国家留学基金资助(201608210308) 张旭秀(1968—),女,博士,教授,研究方向为分数阶微积分理论及应用、智能控制等; 李卫东(1963—),男,博士,教授,研究方向为铁路信息与通信智能化技术、复杂系统分析与控制、智能控制等; 盛 虎(1978—),男,博士,副教授,研究方向分数阶微积分理论及应用; 丁鸣艳(1979—),女,硕士,讲师,研究方向为自动控制理论与应用。 张旭秀 10.15938/j.emc.2017.06.013 TN 713 A 1007-449X(2017)06-0096-08
1 一种基于Bode图的有理函数逼近公式的导出
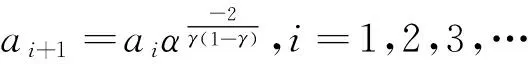
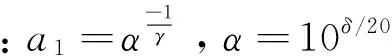
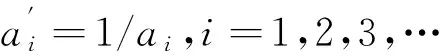
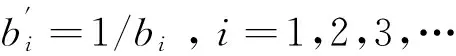


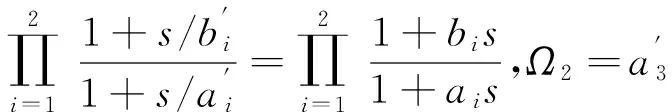
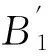

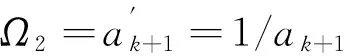
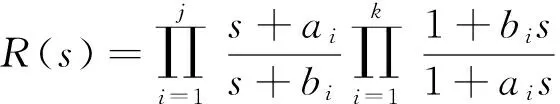
2 逼近误差带宽的设定——逼近函数阶数最小化措施之一
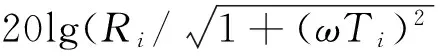
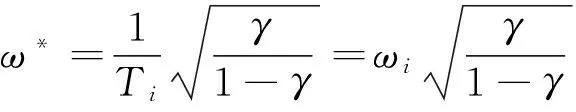
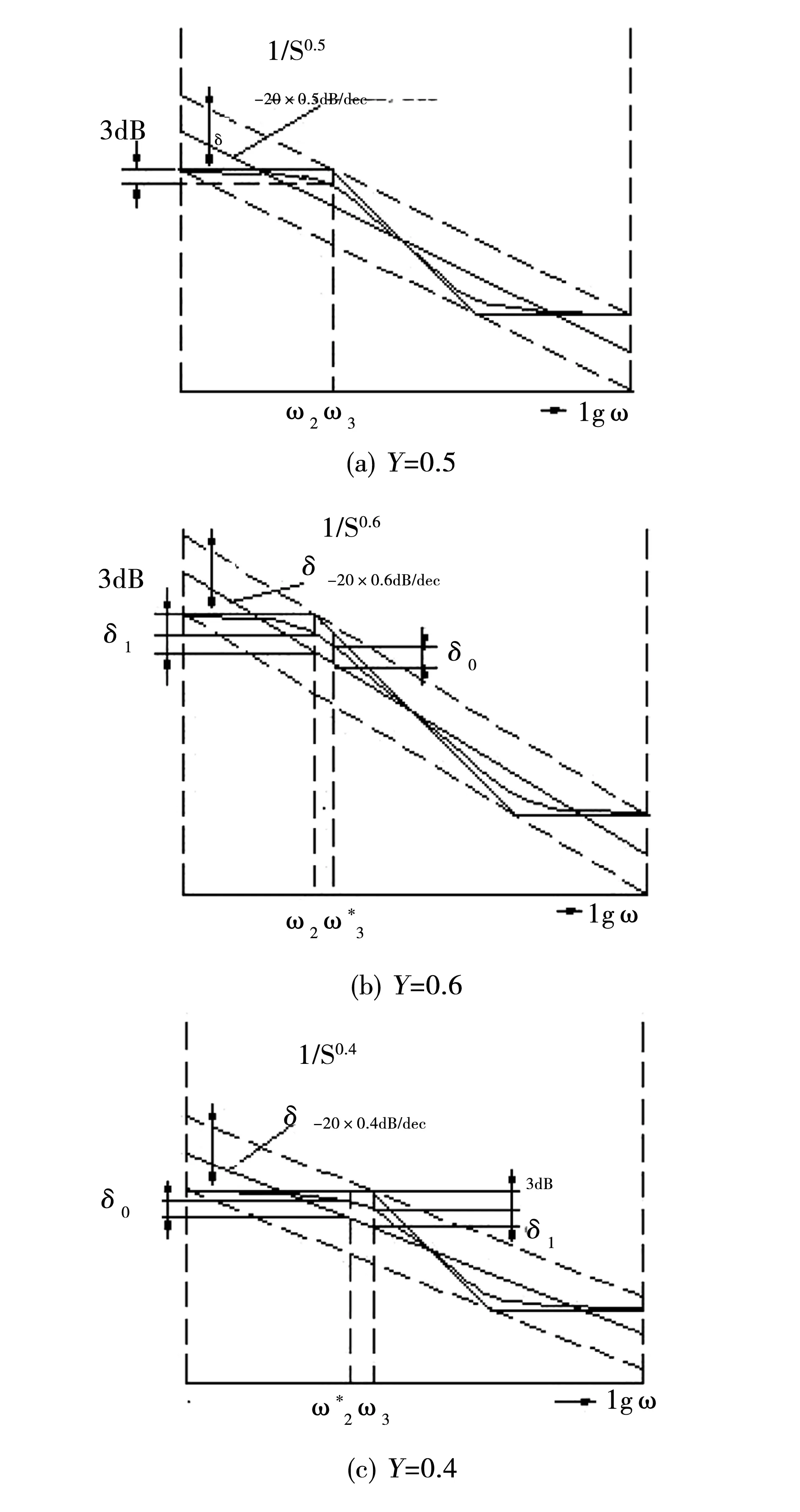
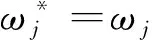
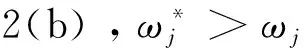
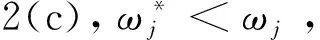
3 应用范围的拓展
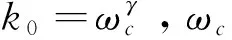

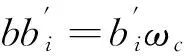
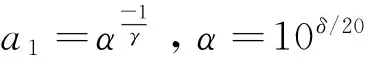
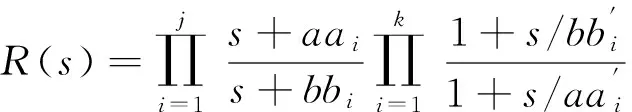
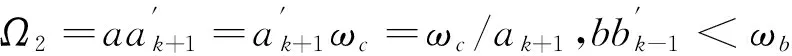
4 有理函数的降阶——逼近函数阶数最小化措施之二


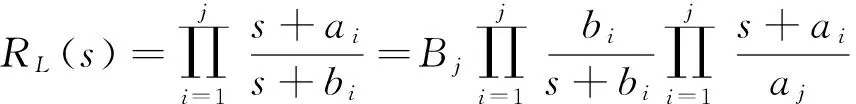
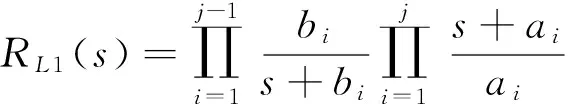
5 实现方法
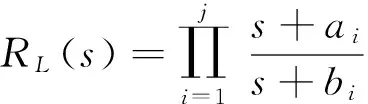
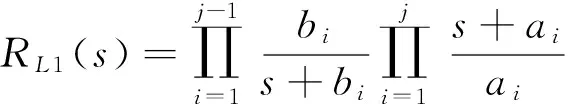

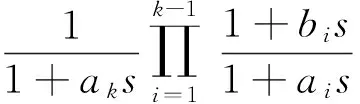
6 验证实例
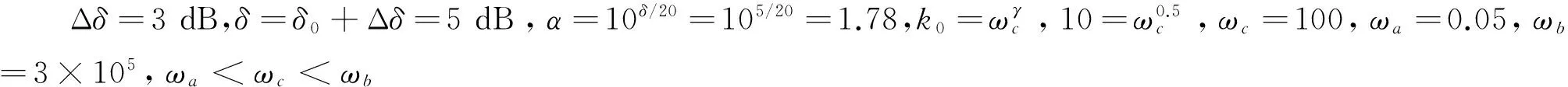
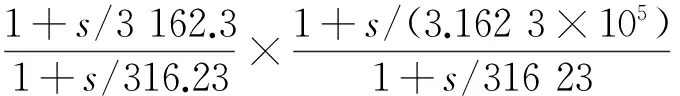
7 结 论
